Lambda函数法计算储层含水饱和度

毕广武

(大庆油田有限责任公司勘探开发研究院, 黑龙江 大庆 163712)

0 引 言

油藏的含水饱和度是自由水界面上的高度和孔隙类型的函数[1],常用压汞法获得毛细管压力曲线计算储层含油(气)饱和度[2-3],方法为沃尔法和油柱高度法。沃尔法获得的饱和度值为油藏的平均原始含水饱和度[4],这种方法不能进行储层连续计算。对构造油藏,为能实现利用毛细管压力曲线进行含水饱和度计算可采用油柱高度法,该法可通过构造毛细管压力曲线实现,做法为建立不同汞饱和度下进汞压力与储层物性(电性参数)之间的关系,或建立不同进汞压力下的汞饱和度与物性(电性参数)之间的关系[5-10]。这种方法为取得更加准确的计算结果,往往需要事先对压汞样品数据进行有效分析,采用不同的技术方法将样品进行合理分类。本文结合A油田的应用,使用Lambda函数在不同进汞压力下对汞饱和度与储层渗透率之间的关系进行了研究,从而构造出毛细管压力曲线,该方法将压汞样品分类及模型建立有机结合,最终实现储层含水饱和度连续计算。

1 Lambda函数法构造毛细管压力曲线

毛细管压力为穿过共同占据岩石孔隙的2个不混溶流体相之间界面的压力差,是与界面张力、润湿角和毛细管半径的相关函数。用压汞法得到的毛细管压力曲线进行地层原始含油(气)饱和度计算,必须将空气汞系统的毛细管压力曲线转化成油藏条件下油(气)水系统毛细管压力曲线。油气要将储层充满,驱动油气进入储层孔隙的浮力必须克服由原始流体和驱替流体之间所产生的毛细管力,即当储层岩石处于饱和状态时,油(气)柱所产生的浮力与储层岩石毛细管压力达到平衡[8,11]。这是毛细管压力曲线计算含油(气)饱和度的基本原理。

Lambda函数法可以很好地描述毛细管压力曲线形状,其有多种不同的描述形式,在Wiltgen等[12]的著作中,方程为

(1)

So=1-Sw

(2)

式中,Sw为含水饱和度,f;So为含油饱和度,f;λ和b为回归常数,取决于孔隙度和渗透率。

函数中参数b和λ在pc—Sw图上的所表征意义:两参数反映表征毛细管压力曲线的函数拟合曲线变化趋势,并无实际物理意义;b值为含水饱和度Sw随压力pc无限增大时所能达到的最小值,λ值为压力pc随含水饱和度Sw无限增大时所能达到的最小值;两参数反映曲线形态上为b值由小变大、λ值由大到变小曲线有向下弯曲趋势,表征样品品质变好,当b越趋于0值同时λ值越小(不等于初始值),样品品质最好。

Lambda函数法构造毛细管压力曲线应用具体步骤:

(1) 对研究区每块压汞样品测定数据进行非线性最优化计算,确定出每块样品式(1)中a、λ和b的参数值。

(2) 建立全部压汞样品a、λ和b参数分别与孔隙度或渗透率的关系图,回归建立参数计算公式。

(3) 利用回归出的a、λ和b参数计算公式,根据式(1)建立出Lambda函数方程,即确定出适应于该研究区的含水饱和度计算模型。

2 Lambda函数在A油田分类应用

A油田岩石类型主要为碎屑岩,属中-低孔隙度、中-低渗透率储层,油藏纵向上表现为上油下水的特点,受构造控制,为构造油藏类型。据此,可应用压汞资料采用油柱高度的方法计算储层含水饱和度。采用上述lambda函数法应用步骤在A油田构造毛细管压力曲线,建立含水饱和度解释模型。

选用A油田物性下限之上22口井119块压汞样品数据进行模型建立。在步骤(1)中参数a、λ和b是在给定初始值后,利用非线性最小二乘法L-M法进行迭代确定。在步骤(2)中分别建立b、λ和a参数与渗透率对数值(logK)的关系图(见图1、图2、图3),从3张关系图上分别可以看出样品数据点可划分为2类,样品品质相对较好的Ⅰ类和样品品质相对较差的Ⅱ类。在b与logK关系图(见图1)中,Ⅰ类样品数据点在b值等于0附近,Ⅱ类样品数据点b值小于-10.0;在λ与logK关系图(见图2)中,Ⅰ类样品数据点λ值大于0.01,Ⅱ类样品数据点λ值为初始值0.01;在a与logK关系图(见图3)中,Ⅰ类样品数据点a值小于12.0,Ⅱ类样品数据点a值大于12.0。图4为2类样品毛细管压力曲线特征图。从图4中可看出2类样品曲线变化趋势明显不同,而同一类样品则有较一致的变化趋势。为实现2类储层在测井上的连续性判别可利用R35值法,式(3)为Winland提出的计算R35值方程公式[1]。在图4中可看出R35=0.7 μm时可作为2类样品分界点。

logR35=0.732+0.588 logK-0.864 logφ

(3)

式中,K为空气渗透率,10-3μm2;φ为孔隙度,%。

通过分类后进行函数参数回归拟合,分别求取出每一类利用logK计算a、b和λ参数的拟合公式(见表1)。分别将表1中每一类参数模型代入到式(1),建立A油田Ⅰ类及Ⅱ类储层含水饱和度计算模型公式。图5和图6分别为Ⅰ类和Ⅱ类模型计算含油饱和度与汞饱和度对比图,全局误差分别为8.9和3.3。

表1 A油田Lambda函数公式各参数拟合公式

图1 A油田Lambda函数b值与log K关系图

图2 A油田Lambda函数λ值与log K关系图

图3 A油田Lambda函数a值与log K关系图

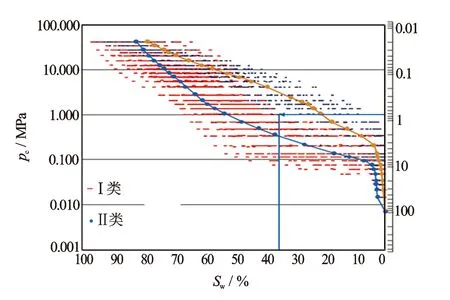
图4 A油田样品分类效果图

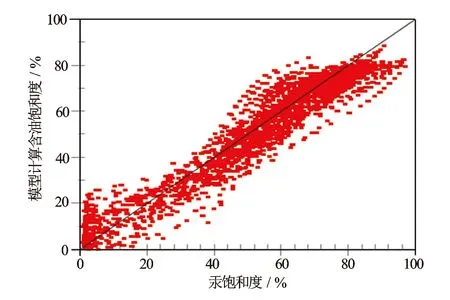
图5 A油田I类模型计算含油饱和度与汞饱和度对比图

图6 A油田II类模型计算含油饱和度与汞饱和度对比图

3 含水饱和度模型效果评价

A油田研究区内钻有1口密闭取心井,通过上述方法对该井取心段进行连续处理(见图7)。该井取心段砂岩层物性较好,深侧向电阻率21.7～32.9 Ω·m,岩性密度2.19～2.27 g/cm3,岩心孔隙度21.1%～23.7%,岩心渗透率(4.89～74.7)×10-3μm2,岩心含油饱和度57.4%～64.4%储层品质较好,均属于Ⅰ类层,模型处理含油饱和度62.6%～66.5%,与岩心含水饱和度对比,平均绝对误差5.1%,平均相对误差8.7%。

图7 密闭取心井处理成果综合图*非法定计量单位,1 mD=9.87×10-4 μm2,下同

4 结 论

(1) Lambda函数参数b和参数λ值在pc-Sw图上可以反映出表征毛细管压力曲线的函数拟合曲线变化趋势,其值大小在一定程度上指示了样品品质;公式中各参数模型的建立和利用R35值法进行储层分类均与储层物性参数渗透率有关,因此储层渗透率模型的精度对处理结果影响较大。

(2) 在A油田应用中利用Lambda函数参数将样品分为品质较好的Ⅰ类和较差的Ⅱ类,每一类有较一致的毛细管压力曲线形态变化特征,对Ⅰ类储层样品可继续分析研究,更进一步划分;由构建的含水饱和度模型进行计算,经与密闭取心分析含水饱和度对比,平均绝对误差5.1%。

参考文献:

[1] Edward A Beaunmont, 诺曼 H 福斯特. 油汽圈闭勘探 [M]. 北京: 石油工业出版社, 2002: 193-319.

[2] 朱家俊, 耿生臣, 林会喜, 等. 也谈压汞资料与含油饱和度的关系 [J]. 大庆石油地质与开发, 2003, 22(5): 34-36.

[3] 林景晔, 张革, 徐喜庆. 复杂油藏原始含油饱和度计算方法 [J]. 大庆石油地质与开发, 2002, 21(3): 32-35.

[4] 杨小磊. 低孔渗储层原始含油饱和度解释方法研究 [J]. 国外测井技术, 2010(177): 10-12.

[5] 李兴丽, 张琳琳, 邢仁东. 利用常规测井物性曲线重构毛细管压力曲线 [J]. 测井技术, 2012, 36(1): 33-36.

[6] 李兴丽, 吕洪志, 张占松, 等. 拟毛细管压力曲线在水淹层评价中的应用 [J]. 测井技术, 2014, 38(5): 622-626.

[7] 李宁, 王波, 邢艳娟, 等. 基于毛细管压力曲线储层自动分类及测井评价 [J]. 测井技术, 2013, 37(6): 653-657.

[8] 赵毅, 施振飞, 朱立华, 等. 构造毛管压力曲线法在A油田储层评价中的应用 [J]. 复杂油气藏, 2014, 7(1): 52-57.

[9] 廖明光, 付晓文. 砂岩储层毛管压力曲线反演模型 [J]. 西南石油学院学报, 2000, 22(4): 5-8.

[10] 刘晓鹏, 肖亮, 张伟. 储层毛管压力曲线构造方法及其应用 [J]. 西南石油大学学报: 自然科学版, 2008, 30(6): 126-130.

[11] 肖亮, 梁晓东, 林雨静. 储层原始含油饱和度评价新方法研究 [J]. 石油地质与工程, 2007, 21(6): 53-55.

[12] Shripad Biniwale, 等. 用水力单元模拟澳大利亚海上油田地质沉积特性和流体饱和度的改进方法 [C]∥测井分析家协会第46届论文集, 2007.

[13] 文政, 赖强, 魏国章, 等. 应用密闭取心分析资料求取饱和度参数 [J]. 大庆石油学院学报, 2006, 30(6): 17-19.

[14] 李郑辰, 钟淑敏, 杨永军. 朝长地区扶余油层储层分类与产能预测 [J]. 地球物理学进展, 2013, 28(5): 2561-2568.