大管径不同井斜油水两相流流型数值模拟

边晓航, 刘军锋,2, 叶天明, 张正超, 许章, 蔡红婷

(1.长江大学地球物理与石油资源学院, 湖北 武汉 430100;2.油气资源与勘探技术教育部重点实验室(长江大学), 湖北 武汉 430100)

0 引 言

在水平井及斜井中由于重力分异,油水两相流流型和局部持水率发生了明显的变化[1],对生产测井仪器的响应特征识别、多相流解释模型建立和各射孔层产出状况的动态监测造成困难[2],需要开展不同流动状况下油水两相流的流型研究。Trallero J L等[3]采用观察法将水平管油水两相流的流型分为6种;Jose G Flores等[4]将上升倾斜管油水两相流分两大类:油连续相和水连续相;Angeli P等[5]采用观察法将水平管油水两相流流型划分为分层波状流、分界面带有液滴的分层波状流和混合流等5类;Rodriguez O M H等[6]模拟了水平管及微斜井管油水两相流的流型变化;金宁德等[7]和Kamila Mydlarz-Gabryk等[8]分别采用电导波动信号和高速摄像头对垂直上升油水两相流的流型进行了监测,并绘制了流型图;吴铁军等[9]制作了不同流动条件下的油水两相流流型图,并讨论了各流型的转变机理;刘军锋等[10]利用测井仪器分析了大管径倾斜管中的油水两相流的分布规律;Rashmi G Walvekar等[11]利用FLUENT模拟了高流速油水两相流所形成的湍流在水平管中的流动情况;顾汉洋等[12]和陈勇[13]利用VOF模型模拟了水平井油水两相流的流动,分析了流型和截面相含率的影响因素。前人对油水两相流流型的研究主要采用物理实验的方式,并且对低流量小管径井筒中油水两相流流动规律研究较多。随着计算机的迅速发展,计算流体力学(CFD)因其克服了传统实验条件有限、费用高、运行周期长等缺点逐渐被应用于流场分析中。本文利用FLUENT中的VOF模型模拟大管径(内径0.124 m)井筒内不同油水混合速度、不同含水率和不同倾角时油水两相流的相分布情况以研究流型的变化规律。

1 模型建立

利用ICEM CFD建立了内径为0.124 m、长度为20 m、倾角为θ的圆管。在截面进行了“O”型网格划分,并对管道内边界层进行了加密处理(见图1)。

图1 几何模型的建立与网格划分

入口Inlet设置为VELOCITY_INLET边界,出口Outlet设置为PRESSURE_OUTLET边界,管道外壁设置为WALL边界。入口为油水混合物,其中水的密度为998 kg/m3,黏度为0.001 Pa·s;油的密度为860 kg/m3,黏度为0.02 Pa·s。

根据赵金印[14]对湍流入口长度的确定,对于光滑壁面的管流,湍流入口长度只与临界雷诺数和管流的入口处扰动条件有关。本文油水两相流流动的雷诺数Re为1 150～17 200,根据文献[14]得到此时管流的入口长度L=(80～90)D,所以管道内流体达到稳定流动的长度L=10～11 m。本文选择在管长为12 m左右观察流型的变化情况(见图1)。

模型中忽略了温度对流场的影响,流体全部视为不可压缩流体,并且管道壁面设定为无滑移壁面。多相流模型选择VOF模型,湍流模型选择k-ε模型并对壁面采用标准壁面函数进行修正。其中VOF模型是设计用来计算2种或者多种不相容流体分界面位置轨迹的方法,其可以更好地反映出多相之间的界面情况。求解动量方程速度与压力的耦合采用PISO算法,其对非定常流动问题适用,并且允许增加所有欠松弛因子的值,以增加收敛速度。当倾角θ=0°时,初始化管道流场上部为油,下部为水[15];其他倾角时,初始化流场内部为油水均匀混合。

2 求解控制方程[16]

2.1 质量守恒方程

(1)

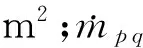
2.2 湍流模型k - ε模型

湍流脉动动能方程(k方程)

Gk+Gb-ρε-YM

(2)

湍流动能扩散率方程(ε方程)

(3)

式中,ρ为流体密度,kg/m3;k为湍流动能,J;ui与ut为均速度,m/s;σk与σε分别为k方程和ε方程的湍流Prandtl数;Gk为平均速度梯度引起的湍动能的产生项;Gb为浮力引起的湍动能的产生项;YM为可压缩湍流中脉动扩张贡献;ε为湍流耗散率,W/m2;μi和μt为湍流黏度,Pa·s;t为时间,s;xi和xj为空间坐标;C1ε=1.44,C2ε=1.92,C3ε=1,均为经验常数。

2.3 标准壁面函数方程

(4)

*非法定计量单位,1 dynes/cm=10 N/m,下同

式中,M为经验常数;Re*为雷诺数;U*为无量纲速度。

3 数值模拟结果分析

3.1 油水两相流流型的划分

Trallero J L[3]利用小管径低流量水平管进行了油水两相流的实验研究,并采用观察法将其流型分为6种。本文通过设置油水混合入口速度vm为0.1～1.5 m/s,含水率分别为10%、40%、60%和80%,倾角分别为±20°、±15°、±10°、±5°和0°进行数值模拟,得到了6种流型(见图2)。定义倾角θ=0°为水平流(流体水平流动),θ>0°为上坡流(流体斜向上流动),θ<0°为下坡流(流体斜向下流动)。由于大管径的影响,并没有得到图2中的油包油-水包水流型,而出现了一种新的流型:油-油包水。

(1) 分层流。出现在油水混合速度较低时,油水两相出现明显的分层并且有清晰连续的液膜分界面。当油水两相斜向上流动(上坡流)时,出现水相局部回流现象;当油水两相斜向下流动(下坡流)时,出现水相流动速度过快、局部持水率较低的现象。

(2) 界面混杂分层流。当油水两相速度进一步增大时,其分界面处的扰动加大使油水两相相互混合。其特征为管子顶部为连续的油相,中部为油水混合相,下部为连续的水相。

(3) 油-油包水。出现在油水比率较大且混合速度较高.下层的水相以水滴的形式分散在油相中而形成油包水,上层为连续的油相。

(4) 油包水。含水率很低油水两相速度很大时,水相全部呈水滴状分散于油相中,形成油包水流型。

(5) 水包油-水。出现在油水比率较小但速度较高,上层的油相以油滴的形式分散在水相中而形成水包油,下层为连续的水相。

(6) 水包油。当含水率很高且油水混合速度较大时,油相全部呈油滴状分散于水相中。

图2 模拟得到的油水两相流流型结构图

3.2 流型图对比分析

经过大量调研国外水平管内的油水两相流流型,发现Trallero J L的流型划分具有典型的代表性,其利用平均压降、管壁压力微分波动、持液率、局部相连续性等,得到了水相折算速度(vws)——油相折算速度(vos)流型图(见图3)。本文利用油水混合速度和入口含水率得到水相-油相的折算速度并绘制了油水两相流的流型图(见图4)。

图3 Trallero J L的实验数据(D=5.013 cm,μo/μw=29.6,ρo/ρw=0.85,σ=36 dynes/cm*, T=25.6 ℃)

图4 数值模拟结果(D=12.4 cm,μo/μw=20,ρo/ρw=0.861,σ=30 dynes/cm, T=25 ℃)

数值模拟出的油水两相流流型转换规律与Trallero J L的基本一致,但分层流的范围变宽,分散流的范围变窄[17],并且没有发现油包水-水包油流型,且出现了油-油包水流型。大管径中的油水两相流更易出现分层流,这是由于管径的增大在一定程度上能够缓冲高流速引起的油水两相界面波动,减少了油水两相的混合,进而保持着分层状态。但在油水两相折算速度都较大的情况下,分层流易向界面混杂分层流转化。同时,发现油-油包水流型和Trallero J L的油包水-水包油流型的范围存在差异,这是因为在油相折算速度很大、水相折算速度很小的情形下,大管径的存在,水相并不能完全混入整个油相形成油包水流型,在管道上部仍然存在连续油相进而形成油-油包水流型。

3.3 不同混合速度、含水率和倾角下流型变化

设置油水混合速度vm为0.1～1.5 m/s,含水率分别为10%、40%、60%和80%,倾角分别为±20°、±15°、±10°、±5°和0°进行数值模拟。经模拟计算得到了不同混合速度、含水率和倾角条件下的流型图(见图5)。

图5 不同混合速度、含水率和倾角条件下的油水两相流流型图

3.3.1 含水率对流型的影响

中高流速(0.65 m/s

3.3.2 混合速度和倾角对流型的影响

如图5(b)所示,当油水混合流速低(0 m/s

3.4 不同混合速度和倾角下持水率的变化

模拟过程中设置油水混合速度vm为0.1～1.5 m/s,含水率为40%,并取倾角θ分别为±10°、±5°和0°进行模拟,得到其持水率Yw随倾角和混合速度的变化规律(见图6)。

井斜倾角θ=0°时,持水率不随流速的增加而改变,持水率为定值(Yw=0.4)。倾角θ>0°(上坡流)时,局部持水率受倾角和流速的影响较大,倾角越大,局部持水率越大;随着流速的增加,倾角小的持水率最先达到定值,且发现当混合速度vm=0.75 m/s时,上坡流中不再出现水相回流现象。倾角θ<0°(下坡流)时,局部持水率随着流速的增加而增加,主要是由于流速导致紊流加剧使底部的水相混入油相中减少了连续水相在底部的加速流动。

图6 不同混合速度、倾角下井筒内持水率变化情况

4 结 论

(1) 根据油水两相界面的总体特征及形态分布将不同状况下的油水两相流流型划分为6种,并模拟出了相应的流型结构图,制作了以油相折算速度-水相折算速度和以混合速度-倾角为坐标的流型图。

(2) 油水两相流流型受混合速度、含水率、倾角等多种因素的影响。当倾角不变时,随着流速的增加,流型由分层流逐渐变为界面混杂分层流,若含水率较高或较低时,流型将为水包油-水、水包油或油-油包水、油包水。低流速情况下流型受倾角影响较大,主要表现在水相回流和水相底部加速流动两方面。

(3) 低流速情况下,井斜倾角对持水率的影响较大。倾角θ>0°时(上坡流),局部持水率偏大;倾角θ<0°时(下坡流),局部持水率偏小。

参考文献:

[1] 宋红伟, 郭海敏, 唐小梅. 水平井及大斜度井油水两相流动模型研究 [J]. 测井技术, 2014, 38(4): 384-390.

[2] 宗艳波, 金宁德, 王振亚, 等. 倾斜油水两相流水为连续相的逆塞流及过渡流型非线性特征 [J]. 计量学报, 2008, 29(5): 449-453.

[3] Trallero J L. A Study of Oil-water Flow Patterns in Horizontal Pipes [C]∥SPE Production & Facilities, SPE Annual Technical Conference and Exhibition(SPE36609), Denver, Colorado, USA, 1997: 165-172.

[4] Jose G Flores, X Tom Chen, Cem Sarica, et al. Characterization of Oil-water Flow Patterns in Vertical and Deviated Wells [C]∥SPE Annual Technical Conference and Exhibition(SPE38810), San Antonio, Texas, USA, 1997: 601-610.

[5] Angeli P, Hewitt G F. Flow Structure in Horizontal Oil Water Flow [J]. International Journal of Multiphase Flow, 2000, 26: 1117-1140.

[6] Rodriguez O M H, Oliemans R V A. Experimental Study on Oil-water Flow in Horizontal and Slightly Inclined Pipes [J]. International Journal of Multiphase Flow, 2006, 32: 323-343.

[7] 金宁德, 宁英男, 王微微, 等. 垂直上升管中油水两相流流型表征 [J]. 化工学报, 2001, 52(10): 907-915.

[8] Kamila Mydlarz-Gabryk, Marcin Pietrzak, Leon Troniewski. Study on Oil-water Two-phase up-flow in Vertical Pipes [J]. Journal of Petroleum Science and Engineering, 2014, 117: 28-36.

[9] 吴铁军, 郭烈锦, 刘文红, 等. 水平管内油水两相流流型及其转换规律研究 [J]. 工程热物理学报, 2002, 23(4): 491-494.

[10] 刘军锋, 郭海敏, 彭原平, 等. 大管径水平管油水两相流动特性实验研究 [J]. 石油天然气学报, 2012, 34(7): 90-93.

[11] Rashmi G Walvekar, Thomas S Y Choong, Hussain S A, et al. Numerical Study of Dispersed Oil-water Turbulent Flow in Horizontal Tube [J]. Journal of Petroleum Science and Engineering, 2009, 65: 123-128.

[12] 顾汉洋, 高晖, 郭烈锦. 水平井油水两相分层紊流流动的数值研究 [J]. 工程热物理学报, 2003, 2(5): 810-812.

[13] 陈勇. 水平管内油水两相流型数值模拟 [J]. 产业与科技论坛, 2014, 13(20): 64-65.

[14] 赵金印. 圆管湍流及入口挡环对圆管湍流影响的实验研究和数值模拟 [D]. 大连: 大连理工大学, 2002.

[15] 许明. 小管径多相流特性及流动参数测量研究 [D]. 合肥: 中国科学技术大学, 2012.

[16] 汪笑楠, 马贵阳, 孙皓, 等. 高含水期水平管油气水三相流动数值模拟 [J]. 石油化工高等学校学报, 2013, 26(5): 78-82.

[17] 娄晨, 彭清华, 林棋. 水平管油-水两相流的流型判别及压降预测 [J]. 油气田环境保护, 2014, 24(2): 12-15.