油水饱和岩石复电阻率频散特性数学模拟

庄显丽, 关继腾, 郑海霞, 杨盈盈

(中国石油大学(华东)理学院, 山东 青岛 266580)

0 引 言

储层岩石复电阻率的频散特性是复电阻率测井的物理基础,近年来,含油储层复电阻率特性的研究主要集中在实验研究[1-5]和理论模拟[6-8]。传统的理论研究普遍推测复电阻率的频散特性是由谐变电流场引起储层孔隙中离子浓度浓差极化和双电层形变形成的一种宏观电化学效应,即复电阻率频散特性的机理应是激发极化效应,但是依据激发极化机理模型无法建立相应的数学模型和定量的模拟方法。近期研究表明,当谐变电流作用于流体饱和储层时,不仅储层内部的电流场和离子流场之间可以相互耦合,电流场和渗流场之间亦可以相互耦合,孔隙液体中的带电离子会受到激发而引起周期性电渗流动[9],产生储层岩石中的电震效应[10]。郑海霞等[11]基于电震耦合理论研究了水饱和储层岩石的复电阻率频散特性,模拟结果与实验结果高度吻合,证明了储层岩石复电阻率的频散现象是由孔隙介质中的电震耦合作用产生的,其微观机理的本质是电渗流作用。

本文基于顾士勇等[12]油水两相饱和储层中震电耦合理论,在郑海霞等[11]含水储层岩石复电阻率频散特性研究的基础上,进一步建立油水饱和岩石中电震耦合波波动方程,数学模拟双电极法测量含油储层岩石复电阻率的频散特性,探讨其微观机制和影响因素。将此方法扩展到气水饱和岩石中,研究了气水饱和岩石复电阻率的频散特性。

1 油水饱和岩石中电震耦合波传播理论

1.1 油水饱和岩石中电震耦合波控制方程

根据油水饱和储层岩石中震电耦合理论[12],仿照文献[11]的研究方法,得到油水饱和岩石中电震耦合波传播控制方程组为

·τ=-ω2(ρu+ρwww+ρowo)

(1)

τ=λ·uI+μ[(u)T+u]-α(Swpw+Sopo)I

(2)

-pw=D1·u+D2·ww+D3·wo

(3)

-po=D4·u+D5·ww+D6·wo

(4)

J=Je+J′=σEe+[σE+L21(-pw+ω2ρwu)]

(5)

(6)

(7)

式中,J为孔隙介质内的总电流密度;J′为因电震耦合产生的电流密度;Je和Ee分别为外接人工电源供入孔隙介质的电流密度和电场强度,其他物理量定义与文献[12]一致。

在孔隙介质中电磁波长远大于弹性波长。相对于弹性波长尺度,可设外源注入电流密度Je均匀分布且与坐标无关。在准静态条件下,式(5)中忽略二次感应电流σE与电震耦合电流L21(-pw+ω2ρwu)的影响,即取

J=Je=σEe

(8)

同理,式(6)可简化为

(9)

1.2 油水饱和岩石中平面电震波波动方程

取Je=Je0e-iω tez,被激发的弹性波沿z方向传播,由油水饱和岩石中电震耦合波传播控制方程,可以导出一维油水饱和岩石中电震耦合波传播方程

(10)

(11)

(12)

式中,D1、D2、D3、D4、D5、D6、N、M1、M2及相关量定义与文献[12]一致,N1=N+μ。

采用傅里叶变换方法求解式(10)、式(11)和式(12)。令Gu、Gww和Gwo分别表示u、ww和wo对应的格林函数,则一维格林函数积分公式可表示为

(13)

(14)

(15)

则由式(10)、式(11)和式(12)可得一维单位电流源激发的电震耦合波动方程

-δ(z-z′)

(16)

(17)

(18)

(19)

(20)

(21)

令式(19)、式(20)和式(21)的系数行列式为0,可得关于电震波传播常数的方程为

lpk6+mpk4+npk2+tp=0

(22)

其中,

lp=N1(D3D5-D2D6)+M1(D1D6-D3D4)+

M2(D2D4-D1D5)

(23)

mp=ω2ρw(D3D4-D1D6-M1D6+M2D5)+

ω2ρo(D1D5-D2D4+M1D3-M2D2)+

(24)

ρwM1-ρD2)+ω4ρw(ρwD6-ρoD3)+

(25)

(26)

求解式(22)便可得到对应于电震快纵波P1波、电震慢纵波P2波和电震慢纵波P3波的3个传播常数kP1、kP2和kP3。

2 油水饱和岩石中复电阻率的求解方法

2.1 供入电流的传播模式

根据双电极法测量油水饱和储层岩石复电阻率的方法,电极注入岩心的电流第1部分JP1用于激发电震快纵波P1波,第2部分JP2用于激发电震慢纵波P2波,第3部分JP3用于激发电震慢纵波P3波,则电流密度J=JP1+JP2+JP3。由于3种模式的电震波传播方向都与电流方向一致,可将电流密度表示为

J=±JP10e±ikP1zez±JP20e±ikP2zez±JP30e±ikP3zez

(27)

式中,JP10、JP20和JP30为电流密度的振幅。

(28)

将正向波和反向波的电流密度的振幅分别记为J+0和J-0,岩心中任一点处总的电流密度为正反向电震波的电流之和。因此,总电流密度可写为

J-0e-ikP2z+J-0e-ikP3z)ez

(29)

对于岩心复电阻率的测量,研究区域是有限的,正反向激励源大小不同,应由边界条件确定。根据谐变电流注入特点,在长度为L的岩心两端供电电极处电流密度相同,设为J0,因此

J|z=0=J|z=L=J0

(30)

将式(29)代入式(30),在z=0处有

J0=J+0+J-0

(31)

在z=L处有

(32)

联立式(31)、式(32),可解得正反向电震波的电流密度振幅与总电流密度振幅之间的关系

(33)

2.2 油水饱和孔隙介质中复电阻率的计算公式

根据电极法测量复电阻率原理,岩心的复电阻率可表示为

(34)

式中,ρ*(ω)为岩石复电阻率;J0为供入电流密度;ΔU为岩心两端电位差;ρR(ω)、ρI(ω)分别为复电阻率的实部和虚部[11]。

根据式(8),岩心中电场强度Ee与电流密度Je的关系可表示为

(35)

式中,ξ=p1,p2,p3,分别对应于电震快纵波P1波、电震慢纵波P2波和电震慢纵波P3波。由电流密度表达式(29)可将岩心中的电场强度表示为

J-0e-ikP2z+J-0e-ikP3z)ez

(36)

(37)

将式(33)和式(37)代入式(34),整理可得长度为L的岩心的复电阻率为

(38)

式(38)即为油水饱和岩石的复电阻率的数学表达式。

3 计算实例与分析

3.1 模拟参数的确定

油水饱和岩石中模拟参数的选取参考文献[11-12],具体参数取值见表1,其中ε0为真空介电常数、μ0为真空磁导率。

3.2 孔隙度对油水饱和岩石复电阻率频散特性的影响

根据式(38),油水饱和岩石中复电阻率的频散特性与孔隙度的变化关系如图1所示。图1(a)考察了10-6～106Hz频段内复电阻率频散特性与孔隙度的变化关系,实心标线代表复电阻率实部,虚心标线代表复电阻率虚部(下同),图1(b)是图1(a)在100～106Hz频段内的截图。

由图1可见,复电阻率的实部随频率的增大呈“阶梯状”下降,复电阻率虚部曲线上有3个清晰的极值。分析可知,10-6～106Hz频段内复电阻率频散曲线中的3次变化分别由电震慢纵波P2波、电震慢纵波P3波和电震快纵波P1波引起的,其中第1次变化,即复电阻率实部第1次快速下降的位置和复电阻率虚部第1极值的位置取决于慢纵波P2波,第2次变化,即复电阻率实部第2次快速下降的位置和复电阻率虚部第2极值的位置取决于慢纵波P3波,第3次变化,即复电阻率实部第3次快速下降的位置和复电阻率虚部第3极值的位置取决于快纵波P1波。由此,不妨将复电阻率虚部第1极值所

表1 油水饱和岩石的基本参数取值表

图1 油水饱和岩石复电阻率频散特性与孔隙度的关系曲线

对应的频率称为慢纵波P2波界面极化频率,复电阻率虚部第2极值所对应的频率称为慢纵波P3波界面极化频率,复电阻率虚部第3极值所对应的频率称为快纵波P1波界面极化频率。图1(b)中100～106Hz频段内复电阻率频散曲线的2次阶梯变化、2个界面极化频率等特征都与大多数实验结果相吻合[6-7,13-14]。

由图1还可以看出,随着孔隙度的增大,复电阻率实部和虚部的绝对值均减小,频散程度减小,产生这一情况的原因在于,孔隙度越大,流体导电能力越强,则复电阻率越小。慢纵波P2波界面极化频率和慢纵波P3波界面极化频率均随随孔隙度的增大而减小,而快纵波P1波界面极化频率不变,这是由于界面极化频率与波速有关,慢纵波P2波和慢纵波P3波的波速均随孔隙度的增大而减小,P1波的波速几乎不受孔隙度的影响。

图2 油水饱和岩石复电阻率频散特性与渗透率的关系曲线

3.3 渗透率对油水饱和岩石复电阻率频散特性的影响

根据式(38),油水饱和岩石中复电阻率的频散特性与渗透率的变化关系如图2所示。图2(a)考察了10-6～106Hz频段内复电阻率频散特性与渗透率的变化关系,图2(b)是图2(a)在100～106Hz频段内的截图。

由图2可以看出,随着渗透率的增大,复电阻率实部和虚部的绝对值均增大,频散程度增大,慢纵波P2波界面极化频率和慢纵波P3波界面极化频率均增大,快纵波P1波界面极化频率几乎不变,这是由于随着渗透率的增大,慢纵波P2波和慢纵波P3波波速增加明显,快纵波P1波波速几乎不受影响。

3.4 饱和度对油水饱和岩石复电阻率频散特性的影响

根据式(38),油水饱和岩石中复电阻率的频散特性与含水饱和度的变化关系如图3所示。图3(a)考察了10-6～106Hz频段内复电阻率频散特性与含水饱和度的变化关系,图3(b)是图3(a)在100～106Hz频段内的截图。

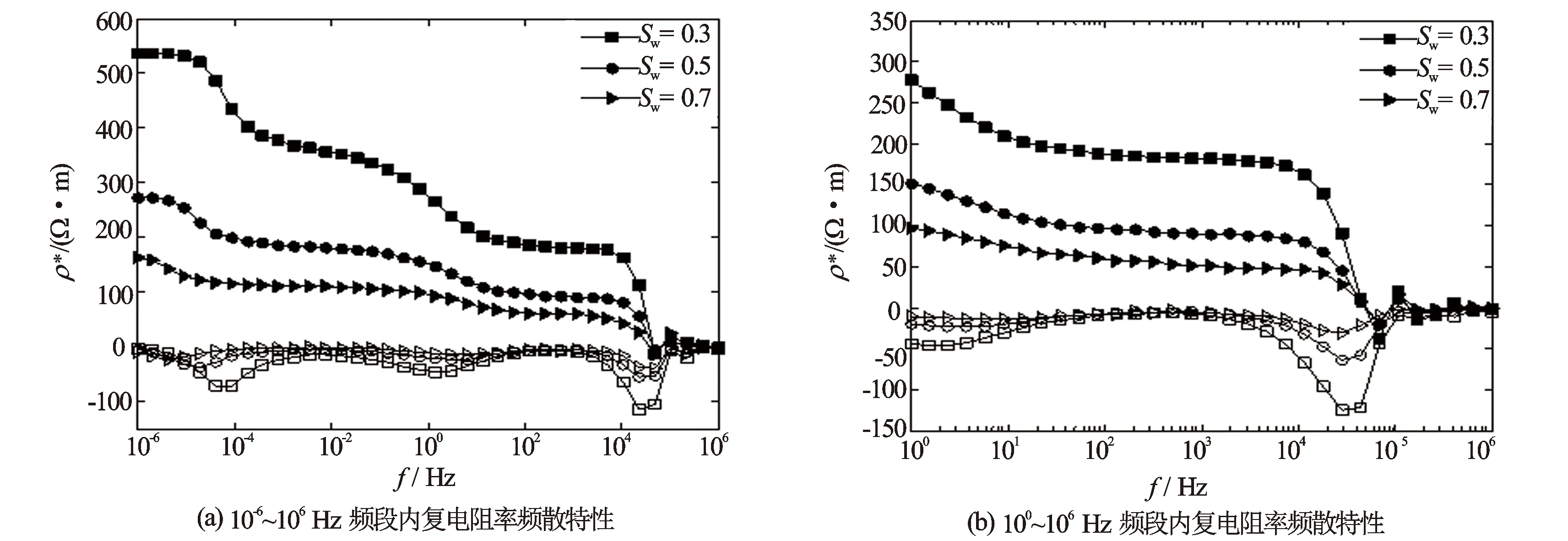
图3 油水饱和岩石复电阻率频散特性与饱和度的关系曲线

由图3可以看出,随着含水饱和度的增大,复电阻率实部和虚部的绝对值均减小,频散程度减小。这是由于含水饱和度越大,流体导电能力越强,则复电阻率越小。随着饱和度的增大,慢纵波P2波界面极化频率减小,慢纵波P3波界面极化频率增大,快纵波P1波界面极化频率略有增大。这是由于随着饱和度的增大,慢纵波P2波波速减小,慢纵波P3波波速增大,而快纵波P1波波速略有增大。

4 气水饱和岩石中复电阻率的模拟与分析

4.1 气水饱和岩石中复电阻率的模拟方法

肖占山等[15]曾对含气泥质砂岩复电阻率频散特性进行了实验研究,这里将油水饱和岩石中的震电耦合理论扩展到气水饱和的情况,在含水储层岩石复电阻率频散特性研究的基础上进一步建立气水饱和岩石中电震耦合波波动方程,数学模拟双电极法测量含气储层岩石复电阻率的频散特性,并探讨其微观机制和影响因素。气水饱和岩石具体模拟参数取值见表2,其中ε0为真空介电常数、μ0为真空磁导率。

4.2 气水与油水饱和岩石复电阻率频散特性对比

根据式(38)和双电极法测量气水岩石复电阻率的数学模型,油水饱和岩石和气水饱和岩石中复电阻率的频散特性如图4所示。图4(a)考察了10-6～106Hz频段内复电阻率实部和虚部随频率的变化关系,图4(b)是图4(a)在100～106Hz频段内的截图。

表2 气水饱和岩石的基本参数取值表

图4 气水与油水饱和岩石复电阻率频散特性对比曲线

由图4可以看出,气水饱和岩石复电阻率频散曲线中实部的第1次、第2次快速下降的位置和虚部的第1极值、第2极值出现的位置挨得很近,不如油水饱和岩石复电阻率频散曲线表现得那么明显,但二者在整体上表现出相同的变化趋势,即二者的频散特性相同,这与文献[15]的研究结果一致。

4.3 孔隙度对气水饱和岩石复电阻率频散特性的影响

气水饱和岩石中复电阻率的频散特性与孔隙度的变化关系模拟结果如图5所示。图5(a)考察了10-6～106Hz频段内复电阻率频散特性与孔隙度的变化关系,图5(b)是图5(a)在100～106Hz频段内的截图。

由图5可以看出,气水饱和岩石复电阻率频散特性与孔隙度的变化关系同油水饱和岩石的情况一致,即随着孔隙度的增大,频散程度减小,慢纵波P2波界面极化频率和慢纵波P3波界面极化频率均减小,快纵波P1波界面极化频率几乎不变。

图5 气水饱和岩石复电阻率频散特性与孔隙度的关系曲线

4.4 渗透率对气水饱和岩石复电阻率频散特性的影响

气水饱和岩石中复电阻率的频散特性与渗透率的变化关系模拟结果如图6所示。图6(a)考察了10-6～106Hz频段内复电阻率频散特性与渗透率的变化关系,图6(b)是图6(a)在100～106Hz频段内的截图。

由图6可以看出,气水饱和岩石复电阻率频散特性与渗透率的变化关系同油水饱和岩石的情况一致,即随着渗透率的增大,频散程度增大,慢纵波P2波界面极化频率和慢纵波P3波界面极化频率均增大,快纵波P1波界面极化频率几乎不变。

图6 气水饱和岩石复电阻率频散特性与渗透率的关系曲线

4.5 饱和度对气水饱和岩石复电阻率频散特性的影响

气水饱和岩石中复电阻率的频散特性与含水饱和度的变化关系模拟结果如图7所示。图7(a)考察了10-6～106Hz频段内复电阻率频散特性与饱和度的变化关系,图7(b)是图7(a)在100～106Hz频段内的截图。

由图7可以看出,气水饱和岩石复电阻率频散特性与饱和度的变化关系同油水饱和岩石的情况一致,即随着含水饱和度的增大,频散程度减小,这与文献[15]的研究结果相吻合;随着含水饱和度的增大,慢纵波P2波界面极化频率减小,慢纵波P3波界面极化频率增大,快纵波P1波界面极化频率略有增大。

图7 气水饱和岩石复电阻率频散特性与饱和度的关系曲线

5 结 论

(1) 基于电震耦合理论研究了油水饱和储层岩石复电阻率的频散特性。油水饱和岩石复电阻率实部频散曲线上有3次快速下降,虚部频段曲线上相对应的有3个极值,这些特征是在电震快纵波P1波、电震慢纵波P2波和电震慢纵波P3波的共同作用下,由岩石中的电渗流机制形成的,界面极化频率出现的位置由电震波的波速决定。

(2) 油水饱和岩石复电阻率的频散程度随着孔隙度、含水饱和度的增大而减小,随着渗透率的增大而增大。慢纵波P2波界面极化频率随孔隙度和含水饱和度的增大而减小,随渗透率的增大而增大,慢纵波P3波界面极化频率随孔隙度的增大而减小,随渗透率和含水饱和度的增大而增大,快纵波P1波界面极化频率随含水饱和度的增大而略有增大。

(3) 气水饱和岩石中复电阻率的频散特性与油水饱和岩石中复电阻率的频散特性略有不同,但二者的频散程度随孔隙度、渗透率和含水饱和度变化关系一致。由于此方面的相关研究甚少,所以气水饱和岩石中复电阻率的频散特性仍需要实验的进一步验证。

参考文献:

[1] 马静, 肖占山, 王东, 等. 复电阻率测井技术的研究进展 [J]. 地球物理学进展, 2008, 23(5): 1586-1591.

[2] 童茂松, 李莉, 姜亦忠, 等. 模拟地层条件的复电阻率自动测量系统研制 [J]. 测井技术, 2005, 29(4): 364-367.

[3] 童茂松, 陶宏根, 丁柱, 等. 高分辨率复电阻率测井仪器设计及现场试验 [J]. 测井技术, 2007, 31(2): 166-168.

[4] 安珊, 李能根. 含水岩石复电阻率的实验研究 [J]. 测井技术, 1998, 22(5): 315-317.

[5] Tong Maosong, Tao Honggen. Permeability Eestimating from Complex Resistivity Measurement of Shaly Sand Reservoir [J]. Geophysical Journal International, 2008, 173(2): 733-739.

[6] 尹成芳, 柯式镇, 张雷洁. 电极型复电阻率扫频系统响应数值模拟 [J]. 测井技术, 2014, 38(3): 273-278.

[7] 姜恩承, 令狐松, 叶青竹, 等. 频率域复电阻率数学模型研究 [J]. 测井技术, 2002, 26(2): 98-100.

[8] 关继腾, 程媛媛, 于华. 利用等效电路模型研究泥质砂岩复电阻率频散特性 [J]. 测井技术, 2011, 35(6): 512-517.

[9] 于华, 关继腾, 陈辉, 等. 储层岩石流动电位频散特性的数学模拟 [J]. 地球物理学报, 2013, 56(2): 676-687.

[10] Pride S R, Haartsen M W. Electroseismic Wave Properties [J]. Acoustical Society of America, 1996, 100(3): 1301-1315.

[11] 郑海霞, 关继腾, 薛庆忠. 基于电震耦合理论研究电极法储层岩石复电阻率频散特性 [J]. 地球物理学报, 2016, 59(6): 2266-2279.

[12] 顾士勇, 关继腾, 张泉滢, 等. 油水两相饱和储层中平面震电波场响应特性 [J]. 地球物理学进展, 2015, 30(4): 1691-1704.

[13] 高杰, 冯启宁, 孙友国. 电极型复电阻率测井方法及其应用 [J]. 石油学报, 2003, 24(4): 62-64, 68.

[14] 柯式镇, 冯启宁, 何亿成, 等. 电极法复电阻率测井研究 [J]. 石油学报, 2006, 27(2): 89-92.

[15] 肖占山, 徐世浙, 罗延钟, 等. 含气泥质砂岩频散特性的实验研究 [J]. 天然气工业, 2006, 26(10): 63-65.