准噶尔盆地玛湖凹陷百口泉组致密砂砾岩孔隙分形特征及影响因素探讨

司马立强, 杨国栋, 吴丰, 王亮, 孟凡

(西南石油大学地球科学与技术学院, 四川 成都 610500)

0 引 言

中国东西部中、新生代陆相含油气盆地碎屑岩储层中砂砾岩储层广泛分布,已在准噶尔盆地的西北缘和东缘、渤海湾盆地济阳坳陷、海拉尔盆地及松辽盆地北部等发现了大量的砂砾岩油气藏,其中以准噶尔盆地玛湖凹陷百口泉组砂砾岩储层的油气勘探与开发最获瞩目。玛湖凹陷百口泉组储层致密,孔隙度普遍较低(小于12%),孔隙结构是影响储层渗流特性及油气能否产出的关键。受玛湖凹陷百口泉组储层岩石成分复杂、粒度变化较大、孔隙类型多样等因素的影响,储层孔隙结构的非均质性较强,孔隙结构的有效表征及评价存在困难。

分形几何的研究对象是非线性系统中具有某种自相似性的现象。所谓分形是指物体的数目与其线性尺度之间存在着幂函数关系,而幂指数就是该物体的分形维数[1]。可利用分形维数对具有分形性质的物体进行表征。不同沉积环境及成岩作用过程造成的孔隙结构特征不同,尽管孔隙结构极不规则,难以用常规参数描述,但孔隙结构具有良好的自相似性,表现出复杂的单分维或多分维特征[2]。

基于储层岩石孔隙结构的分形特征,利用分形理论计算储层分形维数,为储层孔隙结构的评价提供了新的思路与手段。储层分形维数的计算模型有毛细管束模型、J函数模型、热力学模型等。Pfeifer等利用氮气吸附曲线计算分形维数,计算结果表明分形维数介于2～3之间[3];Katz等利用扫描电镜提取参数计算分形维数,其范围为2～3;分形维数越大,孔隙结构非均质性越强[4];Shen P等根据压汞毛细管压力曲线利用毛细管束模型计算分形维数,发现小孔隙具有分形特征,而大孔隙部分不具有分形特征[5];徐守余、张婷等研究显示毛细管束分形模型、J函数模型能有效表征砂岩储层孔隙分形特征[6-7];郭春华、张陈珺等采用热力学模型研究了页岩的孔隙分形特征,取得了较好的效果[8-9];安士凯、杨宇等采用热力学模型对煤层的孔隙分形特征进行了分析[10-11]。文献调研显示,毛细管束模型、J函数模型、热力学模型等所计算的分形维数在砂岩、页岩、煤层孔隙结构评价中取得了较好效果。但是,利用分形维数对致密砂砾岩储层孔隙结构特征的研究还未见报道。对致密砂砾岩储层孔隙分形特征的研究需探讨适合于致密砂砾岩储层的分形维数计算模型,并针对致密砂砾岩储层特征分析其影响因素。

本文基于准噶尔盆地玛湖凹陷百口泉组48块致密砂砾岩样品的压汞毛细管压力曲线,采用多种模型计算储层分形维数;根据储层参数与分形维数的关系,提出了适应于致密砂砾岩储层的分形模型;在此基础上,进一步对分形维数的影响因素进行了分析。

1 分形维数的计算及物理意义

压汞毛细管压力曲线的形态能定性反映储层孔径范围,即表征储层孔隙结构;基于压汞毛细管压力曲线提取分形维数定量表征储层孔隙结构的分形模型有J(pc,K,φ)函数曲线模型、毛细管束模型、热力学模型等。为确定孔隙结构分形模型表征的有效方法,需利用各模型计算分形维数,并对比其计算结果。

1.1 J(pc,K,φ)函数曲线分形模型计算分形维数

Leverett M C将实测岩心毛细管压力与参考毛细管压力的比值定义为岩心的J(pc,K,φ)函数[12]

(1)

式中,J(pc,K,φ)为J函数,无因次量;pc为毛细管压力,MPa;σ为界面张力,mN/m;θ为润湿相接触角,(°);K为渗透率,mD*非法定计量单位,1 mD=9.87×10-4 μm2,下同;φ为孔隙度,%。

贺承祖等根据式(1)推导出润湿相流体饱和度Shg与J(pc,K,φ)函数关系[13]

(2)

对式(2)两边求对数,经过推导可得

(D-3) lgJ(pc,K,φ)

(3)

式中,SHg为润湿相饱和度,%;D为分形维数;f为毛细管弯曲度。对式(3)做lgSHg和lgJ(pc,K,φ)双对数坐标图,拟合直线的斜率为D-3。

图1为J(pc,K,φ)函数曲线分形模型计算分形维数的实例,A7样品分形维数为2.829,拟合数据相关性较好。然而,拟合曲线有明显的拐点[见图1(a)],表明不同半径的孔喉具有不同的分形特征。根据样品孔喉半径分布规律拟合出相应的曲线斜率,得到大、小孔隙的分形维数D1和D2[见图1(b)、表1],对比大、小孔隙分形维数,表明岩石大孔隙非均质性更强。

图1 J(pc,K,φ)函数分形模型计算岩心整体分形和分段分形拟合曲线(A7样品)

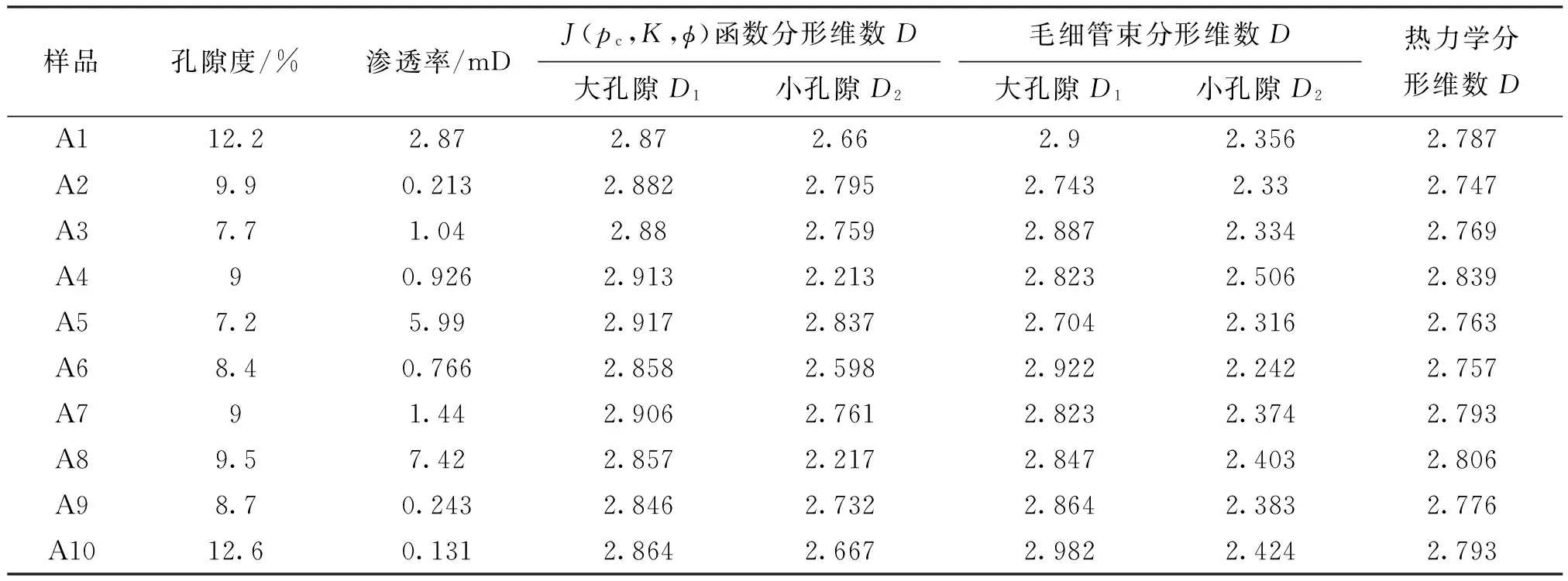
样品孔隙度/%渗透率/mDJ(pc,K,ϕ)函数分形维数D大孔隙D1小孔隙D2毛细管束分形维数D大孔隙D1小孔隙D2热力学分形维数DA112.22.872.872.662.92.3562.787A29.90.2132.8822.7952.7432.332.747A37.71.042.882.7592.8872.3342.769A490.9262.9132.2132.8232.5062.839A57.25.992.9172.8372.7042.3162.763A68.40.7662.8582.5982.9222.2422.757A791.442.9062.7612.8232.3742.793A89.57.422.8572.2172.8472.4032.806A98.70.2432.8462.7322.8642.3832.776A1012.60.1312.8642.6672.9822.4242.793

1.2 毛细管束分形模型计算分形维数

毛细管压力可以提供相应的孔喉特征及其分布信息。根据毛细管模型,有[14]

(4)

式中,N为孔喉数量;VHg为累计进汞量,m3;l为毛细管长度,cm;r为孔喉半径,μm。

式(4)直接反映出孔径和孔隙体积的关系,应用压汞实验数据求取孔隙结构分形维数。根据分形几何理论推导公式可得

(5)

式中,SHg为非润湿相(汞)的累计体积,m3;a为常数。

根据压汞实验数据绘制lgSHg—lgpc交会图,用线性回归法拟合得到直线的斜率为D+2。

图2为A7样品应用毛细管束模型计算分形维数的实例。A7样品分形维数为2.525,拟合数据相关性较好,但拟合曲线同样具有明显拐点[见图2(a)],分段拟合计算的大孔隙分形维数为2.823,小孔隙分形维数为2.374。研究区部分样品分形维数计算结果见表1。相比J(pc,K,φ)函数曲线分形模型,毛细管束分形模型表征的大孔隙非均质性更强。

1.3 热力学分形模型计算分形维数

压汞实验中进汞量和孔隙表面能存在相关性。张保全等提出热力学分形模型[15],有

dW=-pdV=-γLcosθdS

(6)

式中,W为孔隙表面能,J/m2;V为孔隙体积,m3;γL为汞与孔表面的表面张力,J/m;S为孔隙表面积,m2。

(7)

(8)

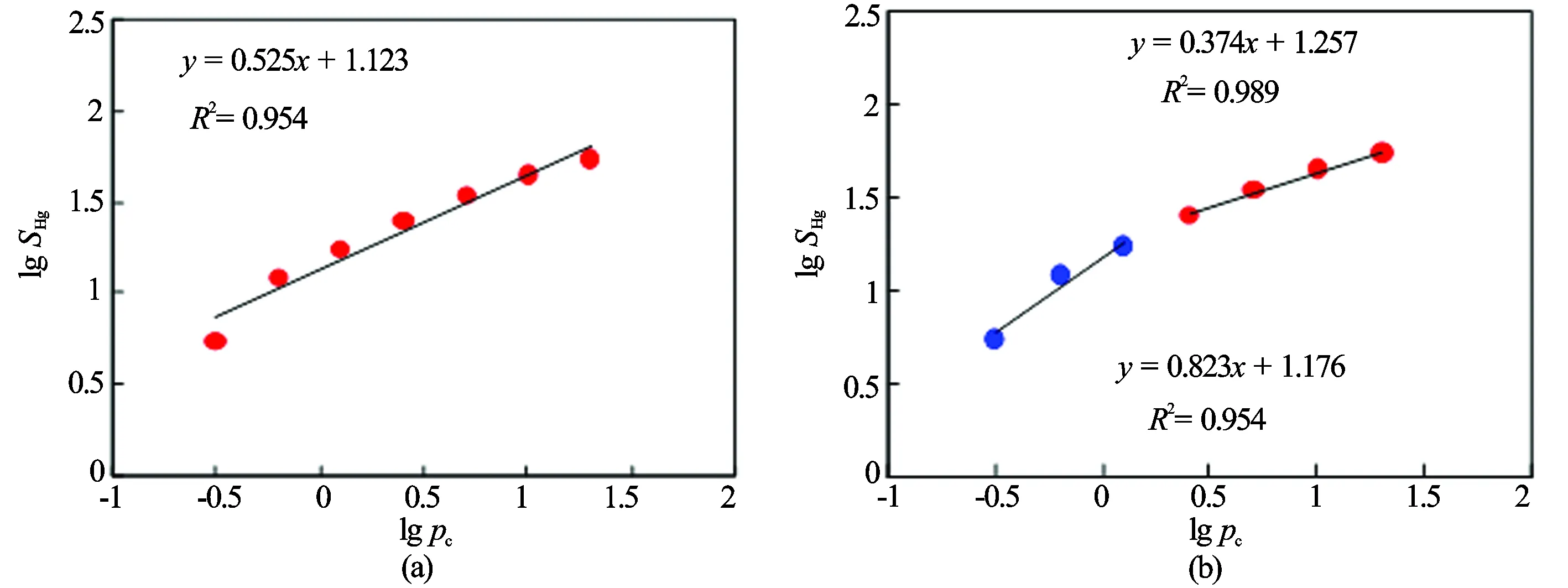
图2 毛细管束模型计算岩心整体分形和分段分形拟合曲线(A7样品)

式中,Wn为累积孔隙表面能,J/m2;pi为第i次进汞压力,MPa;ΔVi为第i次进汞量,m3;Qn为进汞增量,m3;Vn为总孔隙体积,m3;rn为第n次进汞对应的孔喉半径,μm。

根据分形理论,结合热力学原理,得到热力学分形模型的计算公式

(9)

式中,C为常数。

根据式(9)绘制双对数坐标图(见图3),拟合直线的斜率为分形维数D。

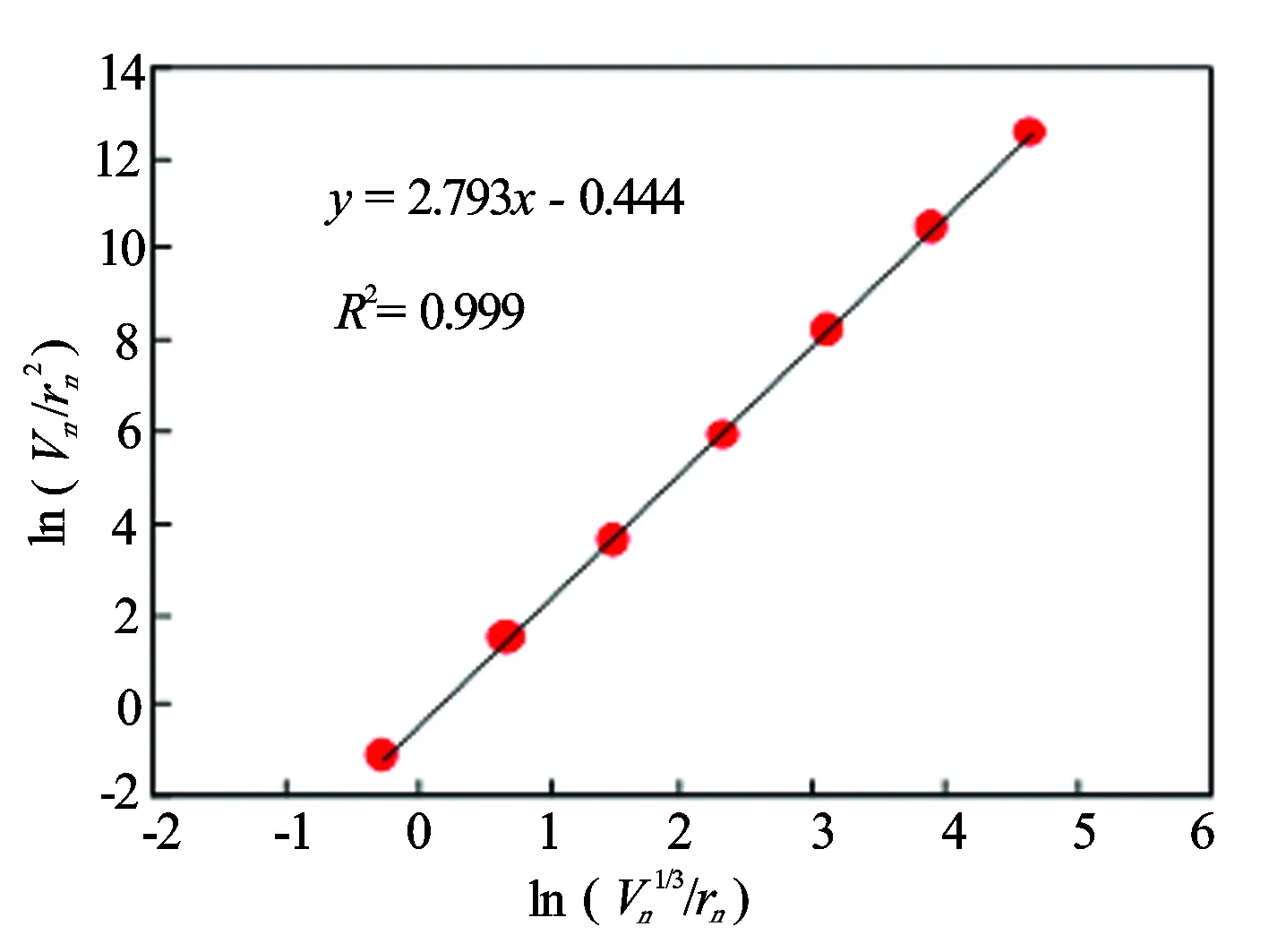
图3 热力学模型计算分形维数拟合曲线(A7样品)

热力学分形模型计算A7样品的分形维数为2.793,分形维数拟合相关性较高(见图3),但难以区分大孔隙和小孔隙分形特征。

对3种模型计算的48块样品分形维数分析发现,J(pc,K,φ)函数计算的大孔隙分形维数为2.823～2.961,小孔隙分形维数为2.217～2.936;毛细管束模型计算的大孔隙分形维数为2.7～2.991,小孔隙分形维数为2.194～2.549;热力学分形模型计算的分形维数为2.633～2.839。对于J(pc,K,φ)函数模型和毛细管束模型计算的大、小孔隙的分形维数通过大、小孔隙的进汞量进行加权平均,得到最终可以表达样品整体孔隙分形特征的分形维数D。

上述3种分形模型分析表明,储层孔隙结构与其线性尺度存在幂函数关系。式(3)、式(5)、式(9)的幂指数就是描述孔隙结构复杂程度的分形维数,可以利用分形维数对储层孔隙结构进行定量表征。分形维数分布范围为2～3,分形维数越小,孔隙形状越规则,孔隙表面越光滑,孔渗关系越好,储层渗流性越好。

2 分形维数表征储层特征

2.1 分形维数与表征储层物性的关系

基于3种分形维数计算模型,利用48块样品分形维数表征储层物性对其效果进行了对比分析,以验证3种模型的适用性;J(pc,K,φ)函数分形模型计算的分形维数随孔隙度的减小而增大,而渗透率与分形维数物无规律[见图4(a1)、(a2)];毛细管束模型分形维数随孔隙度、渗透率的减小而增大,但毛细管束模型分形维数与渗透率相关性更高[见图4(b1)、(b2)]。热力学分形模型计算的分形维数与孔隙度无规律,分形维数随渗透率的降低而增大,但增大程度不明显[见图4(c1)、(c2)];对比分析结果表明,毛细管束模型分形维数与储层物性的变化规律吻合最好,该分形维数能定量表征储层物性。

2.2 分形维数表征储层孔喉特征

图4 分形维数与孔隙度、渗透率的关系

利用48块样品分形维数表征储层孔喉特征,对比分析各模型所计算分形维数与孔喉特征参数之间的关系。对比分析结果表明,J(pc,K,φ)函数模型与储层孔喉特征参数无明显规律,不能很好地表征储层孔隙结构特征[见图5(a1)、(a2)、(a3)];而毛细管束模型分形维数与孔喉特征参数有较好的相关性,分形维数随着分选系数的减小、排驱压力的增大和最大孔喉半径的减小而增大,表明孔喉分布越不均匀,储层储集性能越差,其分形维数越接近于3.0[见图5(b1)、(b2)、(b3)];热力学模型计算的分形维数和孔隙结构参数无规律,且分形维数为2.6～3.0[见图5(c1)、(c2)、(c3)]。

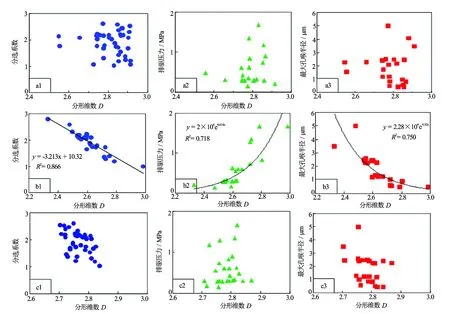
图5 分形维数与孔隙结构特征参数的关系

综合分析表明,分形维数越大,孔隙度、渗透率、分选系数、最大孔喉半径越小,排驱压力越大。分形维数与各孔喉参数表现出较好的相关性。毛细管束分形模型计算的分形维数可以更好地表征致密砂砾岩储层孔隙结构及相关参数。

3 分形维数影响因素分析

3.1 岩石颗粒粒度

岩石颗粒粒度大小分布、粒度分选及磨圆程度可影响储层岩石孔隙结构。分析表明,实验样品A5、A7、A9粒级分布为6～40 mm,以小中砾石和大中砾石为主,样品A5的计算分形维数为2.476,相对其他样品分形维数较小;实验样品A2、A3粒级为2.5～8 mm,以细砾石为主;实验样品A1、A4粒级为0.3～2.5 mm,以粗砂为主。分析粒级分布特征与分形维数的关系表明,研究区储层岩石粒级与分形维数无规律(见图6)。岩石颗粒粒度对研究区致密砂砾岩的分形维数影响不明显。

图6 研究区致密砂砾岩粒度分布特征与分形维数的关系

3.2 碎屑成分

岩石碎屑成分是影响储层孔隙结构的关键因素。研究区致密砂砾岩岩屑包含凝灰岩、 花岗岩等火山岩岩屑以及砂质成分的石英和长石。分析岩屑成分含量与分形维数的关系表明,分形维数与凝灰岩含量具有明显的线性正相关关系,花岗岩、长石及石英的含量与分形维数无规律(见图7)。致密砂砾岩储层半塑性凝灰岩含量较高且易发生形变,造成粒间孔隙和喉道数目减少,孔喉半径减小,孔隙结构、物性变差,导致分形维数增大。凝灰岩含量的变化引起砾岩储层孔隙结构强非均质性。碎屑成分是分形维数的影响因素之一。

3.3 黏土矿物

19块岩心样品黏土矿物与分形维数统计分析结果表明,分形维数随高岭石含量的增加而减小,呈负相关关系;伊利石、伊与蒙混层、绿泥石与分形维数没有表现出较好的相关关系(见图8)。岩石薄片镜下观察显示,高岭石溶蚀孔及高岭石晶间孔,对储层物性、孔隙结构具有改善作用,导致分形维数减小。黏土矿物中高岭石是影响分形维数的因素之一。

图7 研究区致密砂砾岩主要岩屑成分与分形维数的关系

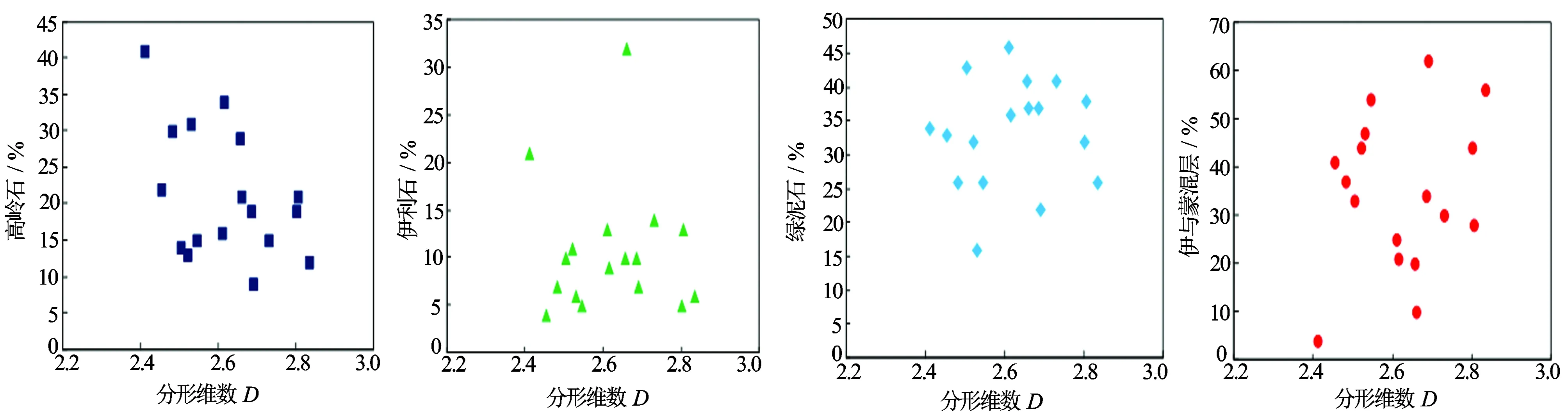
图8 研究区致密砂砾岩黏土矿物与分形维数的关系

图9 研究区致密砂砾岩储层孔隙类型

3.4 孔隙类型

孔喉形态的复杂程度直接决定分形维数的大小。研究区致密砂砾岩储层岩石薄片表明,储层孔隙类型以剩余粒间孔、粒内溶孔为主,微裂缝和晶间孔次之(见图9)。储层孔隙类型以多种组合形式存在,孔隙结构复杂,孔喉形态多以条状、管束状为主。毛细管束分形模型计算的分形维数可以较准确地反映其孔隙结构的复杂程度。

图10 研究区产能与分形维数的关系图*非法定计量单位,1 ft=12 in=0.304 8 m,下同

4 分形维数的应用实例分析

分析研究区7口井10个试油层段产能与分形维数的关系结果显示,产能越大,分形维数越小。图10(a)M131井日产油9.24 t,试油层段岩心最大进汞饱和度大,排驱压力小,孔喉分布范围为0.035～4.59 μm,分形维数值为2.427;图10(b)X93井日产油3.45 t,试油层段岩心最大进汞饱和度小,排驱压力大,孔喉分布范围为0.035～2.295 μm,分形维数值为2.691。表2为研究区7口井10个试油层段试油产能与分形维数的关系表。表2进一步显示产能越大,有效评价储层产能的大小。

分形维数越小。利用分形维数的高低可以

5 结 论

(1) 毛细管束分形模型、J函数模型均可以区分致密砂砾岩的大孔隙和小孔隙,但毛细管束分形模型计算的小孔隙分形维数跨度较小,范围2.194～2.549;热力学模型则无法区分大孔隙和小孔隙。

(2) 孔隙度、渗透率、分选系数、最大孔喉半径越小,排驱压力越大,则分形维数越大;孔隙度、渗透率、孔隙结构特征参数与毛细管束模型分形维数具有较好的相关性。

(3) 半塑性凝灰岩为主的碎屑成分、黏土矿物中高岭石是致密砂砾岩储层分形维数的主要影响因素。孔隙类型及形态的复杂程度直接影响分形模型的适用性。

(4) 研究区试油产能越大,分形维数越小,产能与分形维数有着密切的关系,可以通过分形维数评价产能大小。

参考文献:

[1] Falcone K. Fractal Geometry Mathematical Foundations and Applications [M]. London: John Wiley and Sons Press, 1996: 171-174.

[2] Chen J D, Wilkison D. Pore Scale Viscous Fingering in Porous Media [J]. Phys, 1985, 55(2): 1892-1896.

[3] Pfeifer P, Avnir D. Chemistry Non-integral Dimensions Between Two and Three [J]. Journal of Chemical Physics, 1983, 7(7): 3369-3558.

[4] Katz A J, Thompson A H. Fractal Sandstone Pores: Implications for Conductivity and Formation [J]. Phys Revlett, 1985, 54(3): 1325-1328.

[5] Shen P, Li K. Quantitative Description for the Heterogeneity of Pore Structure by Using Mercury Capillary Pressure Curves [C]∥Paper 29996-MS Presented at the International Meeting on Petroleum Engineering, 14-17 November 1995, Beijing, China.

[6] 徐守余, 王淑萍. 砂岩储层微观孔隙结构分形特征研究 [J]. 天然气地球科学, 2013, 24(5): 887-893.

[7] 张婷, 徐守余, 杨珂. 储层微观孔隙结构分形维数应用 [J]. 大庆石油学院学报, 2010, 34(3): 44-46.

[8] 郭春华, 周文, 林璠. 页岩气储层毛细管压力曲线分形特征 [J]. 成都理工大学学报, 2014, 41(6): 773-776.

[9] 张陈珺, 郭平, 熊健. 川南龙马溪组页岩孔隙分形特征 [J]. 复杂油气藏, 2014, 7(4): 15-18.

[10] 安士凯, 桑树勋, 李仰民, 等. 沁水盆地南部高煤级煤储层孔隙分形特征 [J]. 中国煤炭地质, 2011, 23(2): 17-21.

[11] 杨宇, 孙晗森, 彭小军, 等. 煤层气储层孔隙结构分形特征定量研究 [J]. 特种油气藏, 2013, 20(1): 31-33.

[12] Tao Gang, Mohan kelkar. A More General Capillary Oressure Curve and it is Estimation from Production Data [C]∥SPE108180-MS, 2007: 124-128.

[13] 贺承祖, 华明琪. 储层孔隙结构的分形几何描述 [J]. 石油与天然气地质, 1998, 19(1): 15-23.

[14] 马立民, 林承焰, 范梦玮. 基于微观孔隙结构分形特征的定量储层分类与评价 [J]. 石油天然气学报, 2012, 34(5): 15-19.

[15] Zhang Baoquan, Li Shaofen. Determination of the Surface Fractal Dimension for Porous Media by Mercury Porosimetry [J]. Industrial & Engineering Chemistry Research, 1995, 34(4): 1383-1386.