低渗透致密砂岩气层产能预测方法研究

范宜仁, 宋岩, 张海涛, 张鹏, 李思

(1.中国石油大学(华东)地球科学与技术学院, 山东 青岛 266580; 2.中国石油大学(华东)CNPC测井重点实验室, 山东 青岛 266580; 3.中国石油长庆油田分公司勘探开发研究院, 陕西 西安 710018; 4.中国石油长庆油田分公司, 陕西 西安 710018; 5.中国石油集团测井有限公司华北事业部, 河北 任丘 062552)

0 引 言

储层产能评价与预测结果可以检验油气勘探的成果,为油气田开发提供最基本的依据[1-2]。产能预测主要有3种方法:①通过平面径向流模型与测井参数结合求得油气产量适用于中高孔隙度渗透率储层,但对于渗流机理复杂、物性参数难以准确计算的低渗透储层精度不高[3];②根据地区经验提取产能敏感参数,在产能分级的基础上应用产能指数法、测试法、解释图版法等建立相应的产能预测模型[4];③通过主成分分析、灰色建模理论、神经网络等建立智能产能估算模型,实现产能预测[5]。上述方法对储层物性参数计算精度有较高要求,在低孔隙度低渗透率致密储层中应用效果较差。

针对致密砂岩含气储层孔渗关系复杂,渗透率计算精度低,导致传统产能预测方法效果较差的问题,本文以鄂尔多斯盆地东部上古生界致密砂岩气层为例,从岩石物理实验出发,结合Biot-Gassmann理论和Xu-White模型,分析储层含气性与弹性参数的关系,提取产能敏感因子,探索从阵列声波测井数据获取表征储层含气量的地层弹性参数,从而建立产能预测模型,以期提高致密砂岩气层产能预测的准确性。

1 基于常规测井资料的气层产能预测

1.1 基于孔隙结构的储层分类

鄂尔多斯盆地东部多层系低渗透砂岩气藏属典型的岩性气藏,受物源、沉积环境的影响,岩石矿物组分多变,纯石英砂岩和岩屑砂岩并存;孔隙结构复杂,储集空间类型多样,原生、次生孔隙并存,非均质性强。对于孔隙结构越好的储层,其产气能力越高,反之亦然。

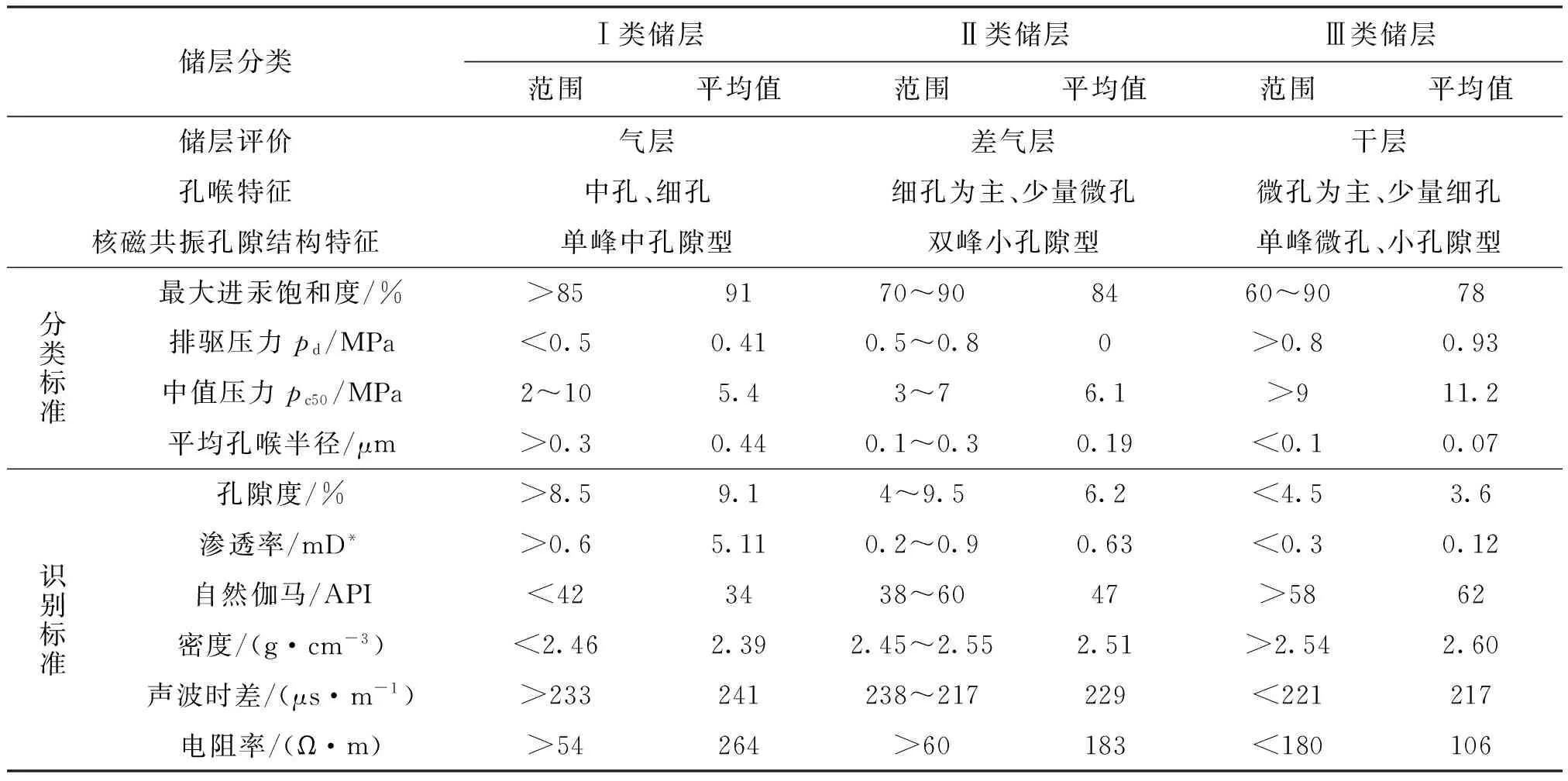
根据研究区20口井50块岩心的压汞和核磁共振实验数据,通过曲线形态及孔喉特征参数对储层孔隙结构特征进行了研究与分析,排驱压力0.18～2.92 MPa,中值压力8 MPa左右,该区大孔隙发育较少,小孔隙占优;平均孔喉半径为0.19 μm,中值孔喉半径分布0.01～0.34 μm,孔喉均值绝大多数小于0.4 μm,孔喉半径整体较小,属微细喉道,以小孔-微细喉为主;微观均质系数0.04～0.23,均质程度较差,表明研究区储层非均质性较强。通过对压汞参数、物性资料及测井数据的综合分析,将该区储层分为3类,各类型孔隙结构的特征、分类标准以及常规测井识别标准等见表1。

1.2 基于常规测井资料产能预测模型

从达西渗流产量公式出发,以相对渗透率与含水饱和度的函数关系为纽带[6],导出油气储层产能与储层有效孔隙度、渗透率以及电阻率之间的理论模型,进而根据常规测井资料计算各层产能。在鄂尔多斯盆地多层合试的试气工艺条件下,总产气量则通过各段气层产能的累加获得。

在油气田开采过程中,油井投产后稳定生产和压差符合平面径向流产量公式

(1)

式中,Qg为气层日产气量,m3/d;C为单位换算系数;K0为渗透率,×10-3μm2;H为气层厚度,m;Tsc为地面标准温度,K;T为气层温度,K;pe为气层压力,MPa;pwf为流动压力, MPa;

psc为地层标准压

*非法定计量单位,1 mD=9.87×10-4μm2,下同

力,MPa;μg为气体黏度,mPa·s;Z为气体偏差系数;re为供气半径,m;rwf为井径,m;S为视表皮系数。

效渗透率K0与绝对渗透率K以及相对渗透率Kro之间关系为

K0=KKro

(2)

相对渗透率与饱和度之间的相关公式为

(3)

式中,e和l分别为对应常数项和指数项系数,将式(2)和式(3)带入式(1),可得储层每米产气指数的表达式

(4)

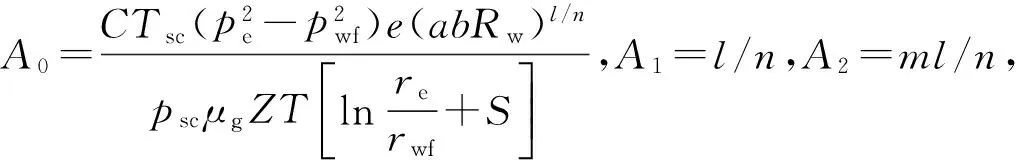
(5)

影响储层产能的主要因素为有效孔隙度、渗透率以及储层电阻率,它们之间为复杂的非线性关系。对于合试气层则采用累加法进行计算,见式(5)。

系数A0、A1、A2可采用最小二乘法、最优化法、神经网络等确定,这里采用麦夸特优化法,该法能克服多项式插值带来的数值振荡,收敛速度快且能有效减小拟合结果的误差。从研究区34个试油层中选取20个层代表性样本点,确定待定系数,14个层作为检验样本,计算不同类型储层对应的A0、A1、A2,结果见表2。实际预测Ⅲ类储层产能时应用Ⅱ类储层模型。

表2 基于常规测井资料产能预测模型系数表

应用上述模型对单层产能计算,再通过累加法求得合试层产能,计算效果见图1,其相关系数为0.81。基于常规测井资料产能预测方法具有一定效果,但由于致密砂岩气层的低渗透性,储层渗透率计算精度低,导致预测效果偏差较大。

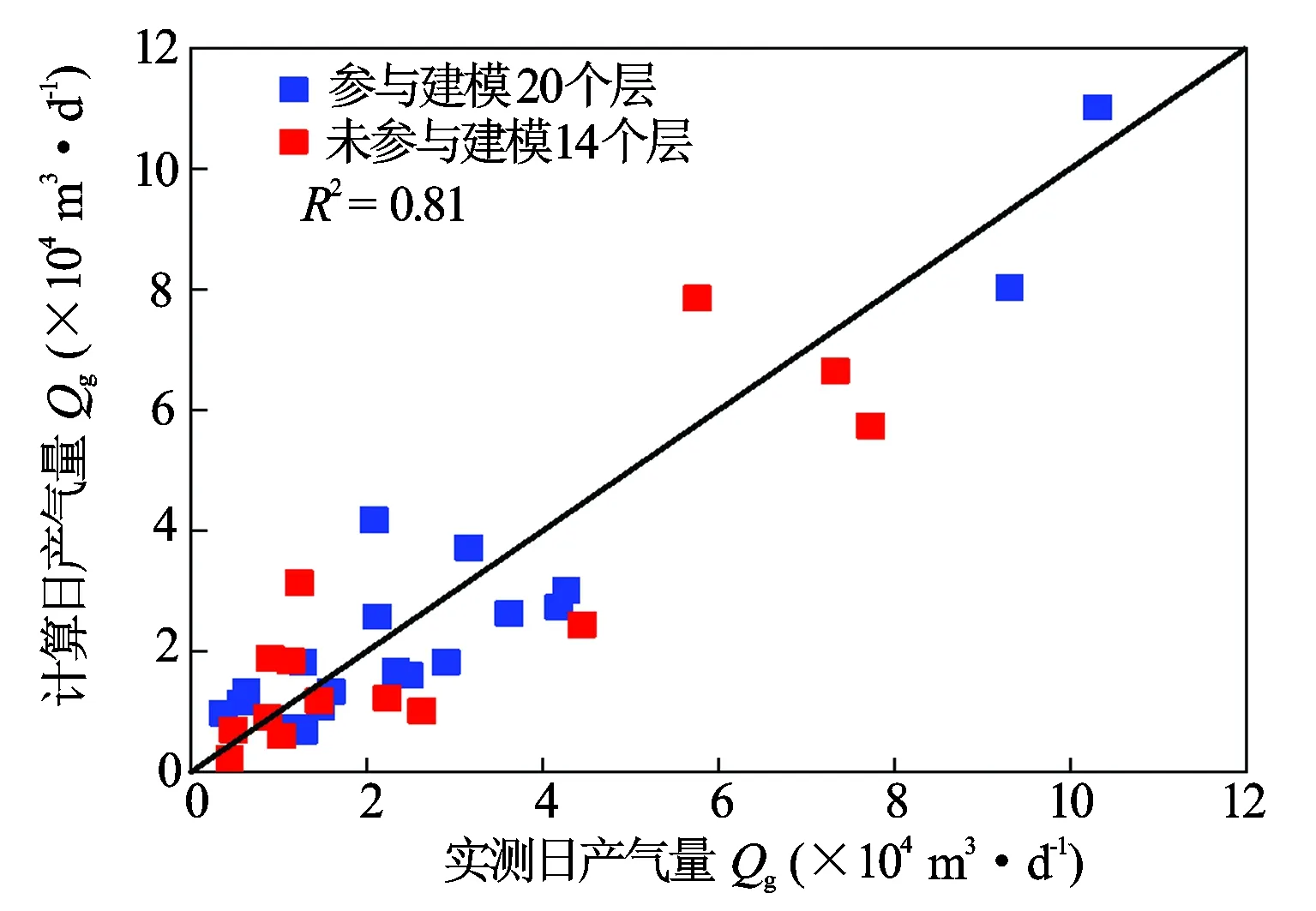
图1 常规方法产能预测效果图

2 基于阵列声波测井的气层产能预测方法

阵列声波测井能够提供反映地层真实骨架和流体特征的声学信息,对储层含气性具有一定的敏感性[8],可利用声学特性实验分析,提取产能敏感因子,建立低渗透致密砂岩气层的产能预测模型。

2.1 致密砂岩声学特性实验分析

2.1.1 含气饱和度和纵横波速的关系

根据威利平均时间公式(Wyllie Time-average Equation)

Δt=(1-φ)Δtma+φΔtf

(6)

式中,Δt、Δtma、Δtf分别为纯岩石、骨架和孔隙流体的声波时差,μs/m;φ为纯岩石的孔隙度,小数。岩性和孔隙度一定时,岩样的纵波时差主要取决于孔隙流体,与含水饱和度存在正相关关系。

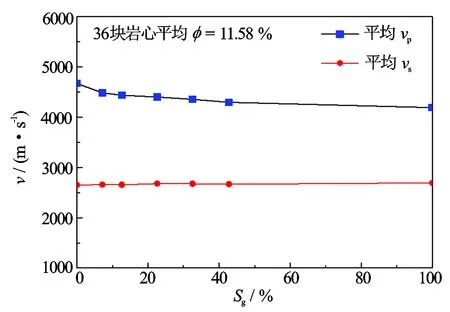
图2 36块岩样平均纵横波速度与含气饱和度关系

图2为常温常压不同饱和度下该地区岩样纵横波速度测试结果。由图2可以看出气水两相条件下随含气饱和度的增加,纵波速度由高变低,干燥砂岩纵波速度最低,饱含水时最高,且含气饱和度在10%左右时纵波速度变化幅度最大。横波速度基本不受含气性的影响。在获得实验数据的同时,基于Krief理论建立石英骨架砂岩体积模型,进行了不同含气饱和度下声波速度的数值模拟计算,模型中骨架密度为2.65 g/cm3,体积模量38.2 GPa,切变模量42.7 GPa,孔隙度为10%,孔隙流体为气和水,其体积模量分别为0.07 GPa、2.73 GPa。数值模拟结果与实验结果相吻合(见图3)。

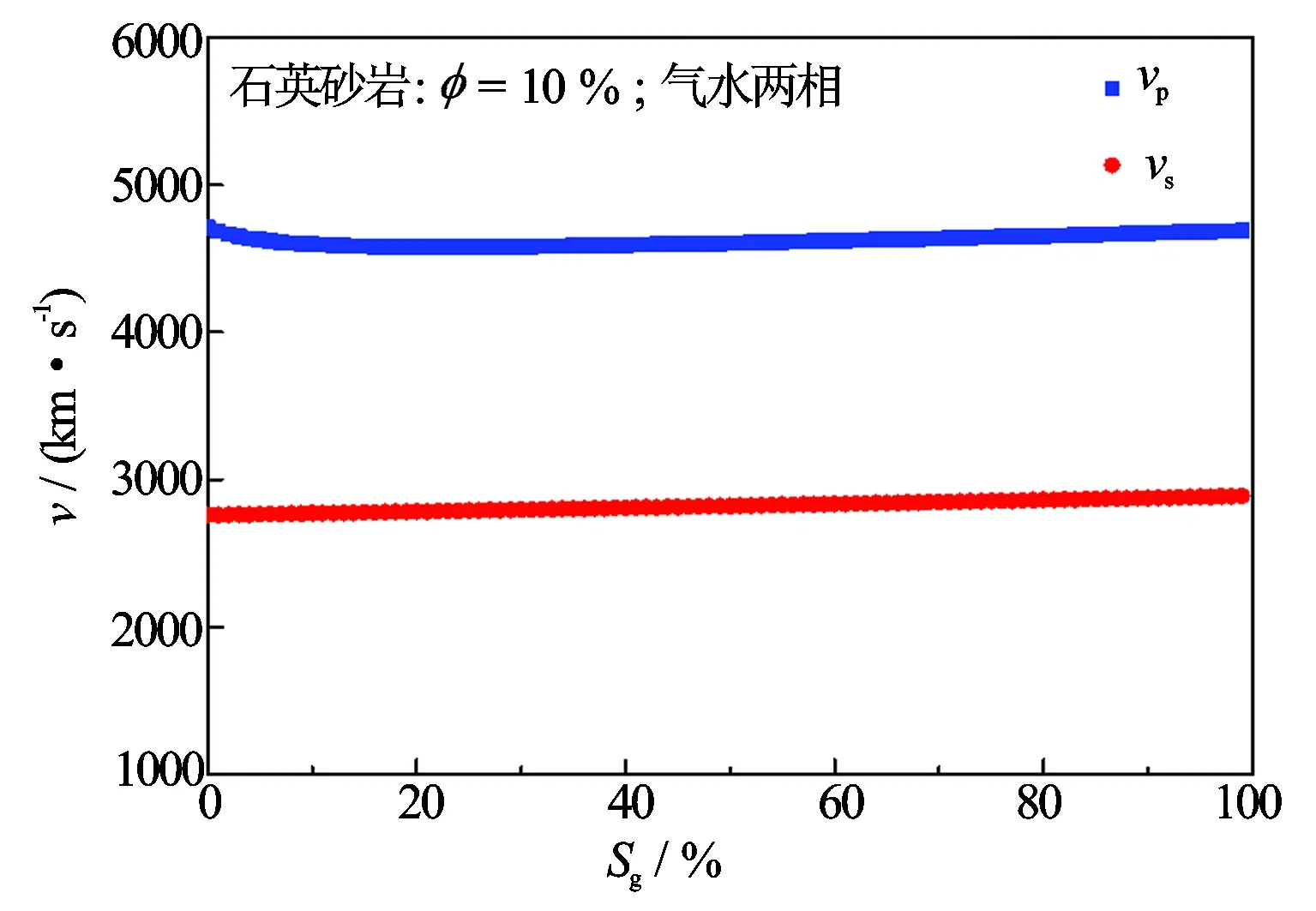
图3 纵横波速度与含气饱和度数值计算结果

2.1.2 含气饱和度和弹性模量的关系

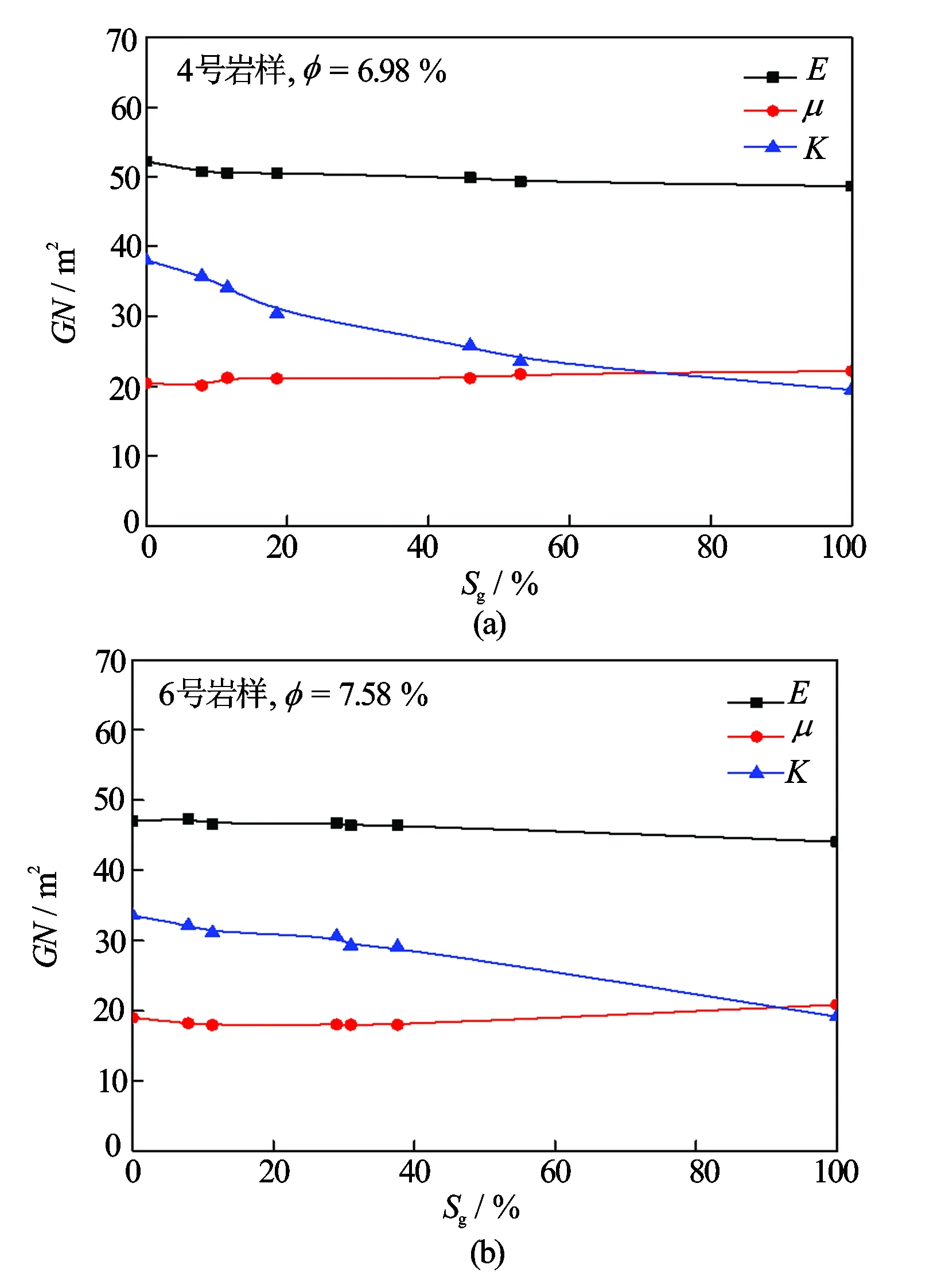
图4 岩心弹性模量与含气饱和度的关系

岩石的弹性性质主要受岩石的孔隙结构、固体相及孔隙流体的影响,反之岩石的弹性性质也能反映岩石的孔隙结构及孔隙流体的性质[9]。岩石的弹性参数主要有泊松比、弹性模量等。实验结果(见图4)表明,岩心含气饱和度对其体积模量的影响最显著,体积模量随含气饱和度增大而减小;弹性模量随含气饱和度增加略有减小,不如体积模量的变化明显;岩心含气饱和度对切变模量的影响很小,岩心切变模量随含气饱和度的增大基本不变。体积模量对储层含气性较为敏感,能更好地反映气层的产能高低。

2.2 构建产能敏感参数2.2.1 构建产能敏感参数——体积模量的差值ΔK

基于对声波实验的研究与分析,当地层100%饱含水时,通过Biot-Gassmann方程预测的100%饱含水储层的体积模量与通过阵列声波测井资料计算的储层体积模量基本相等,其差值ΔK=0;当储层含气时,预测其100%饱含水的体积模量与实际阵列声波测井资料计算的体积模量的差值ΔK>0,ΔK越大,说明含气越多,产能Qi越高。

ΔK=Ksat-K

(7)

(8)

(9)

式中,K为阵列测井声波资料计算体积模量;ρ为密度测井数据;vp为纵波波速;vs为横波波速;Ksat为饱含流体岩石的体积模量;Kdry为干岩石的体积模量;Km为岩石基质的体积模量;Kfl为流体的体积模量。Ksat通过低频条件下的Biot-Gassmann理论进行预测[10]见式(9);Kdry则应用徐怀特模型结合Gassmann方程、Kuster-Toksoz理论以及有效差分介质(DEM)理论进行求解[11-12]。

2.2.2 构建产能敏感参数:含气饱和度指示因子Ig

根据阵列声波测井资料计算得到的体积模量,结合Xu-White模型计算的干岩石骨架体积模量Km,可以求得孔隙流体体积模量Kfl如式(10),进而应用含气饱和度声波岩石物理模型A.Brie公式计算近似含水饱和度Sw

(10)

(11)

式中,e为地区经验参数,通常为2～5。通过体积模量构建含气饱和度指示因子Ig,Ig越大,则气层产量Q0越高。

(12)

通过构建的参数ΔK和Ig即可建立对应的产能预测模型,准确建模的前提是求准干岩石骨架体积模量Kdry。

2.2.3 应用Xu-White模型计算干岩石骨架的体积模量

Xu和White[13-14]基于Gassmann方程、Kuster-Toksoz理论以及有效差分介质(DEM)理论提出了一种利用孔隙度和泥质含量估算砂泥岩纵横波速度的混合介质模型,即Xu-White模型。该模型假定岩石的总孔隙空间由与砂岩颗粒和泥岩颗粒(包含束缚水)相关的孔隙组成(见图5)。

图5 Xu-White模型示意图

Xu-White模型综合考虑了岩石基质性质、孔隙大小、孔隙形状以及孔隙流体性质的影响,其本质是认为这2种孔隙空间的几何形状(孔隙纵横比)差异较大,砂岩具有较大的孔隙纵横比,而泥岩具有较小的孔隙纵横比,因而对弹性模量的影响存在差异。孔隙空间按照矿物、黏土体积各自所占的百分比为

(13)

式中,φ为总孔隙度;φs为砂岩孔隙度;φc为泥质(黏土)孔隙度;νs和νc分别为砂岩和泥岩体积百分比,其中νs=1-φ-νc。

为简化计算,Key和Xu[15-16]假定干岩石骨架的泊松比近似不随孔隙度变化,将上述求解问题转换成一个线性常微分方程组的求解,干岩石骨架弹性模量近似表达为

Kdry=Km(1-φ)p

(14)

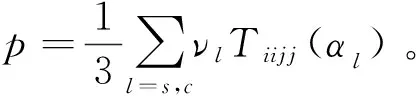
(15)

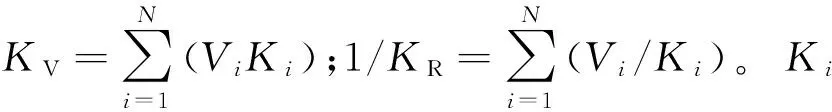
2.3 基于阵列声波测井的产能预测模型

应用上述模型计算构建的产能敏感参数ΔK与Ig所选取的一些参数及初始值见表3,其中岩石骨架的体积模量、骨架密度及骨架声波为通过岩石物理实验获得,气体、泥岩和纯水的体积模量、流体密度、流体声波、e值及泥岩截止值为地区经验值,基于阵列声波测井资料,对产能敏感参数进行求取。

表3 计算产能敏感参数时采用的参数及初值表

结合试气资料,首先分析ΔK、Ig与Q0的相关关系如图6、图7,其相关关系较好,产能与ΔK为线性关系,与Ig为指数关系,其中Q0是通过单层试气产量与单层有效厚度作对比获得。

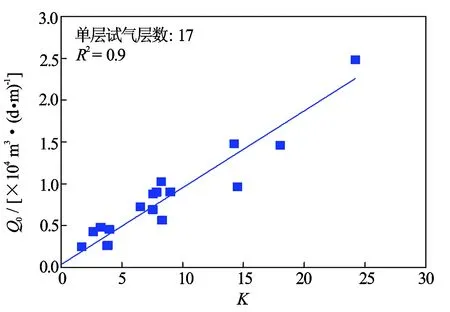
图6 每米日产气和体积模量差值交会图

综合2个敏感因子,从研究区17个有阵列声波测井资料的试气层中选取12个单层试气层进行建模,预测模型见表4。Ⅰ类储层与Ⅱ类储层预测模型都具有较高相关系数,分别为0.94和0.95。

应用上述预测模型,对研究区全部22个有阵列声波测井资料的试气层进行预测,合试气层采用累加法求取见式(5),计算效果图如图8。实测产量与预测产量具有较好的相关性,相对于常规预测方法,误差更小,精度更好。

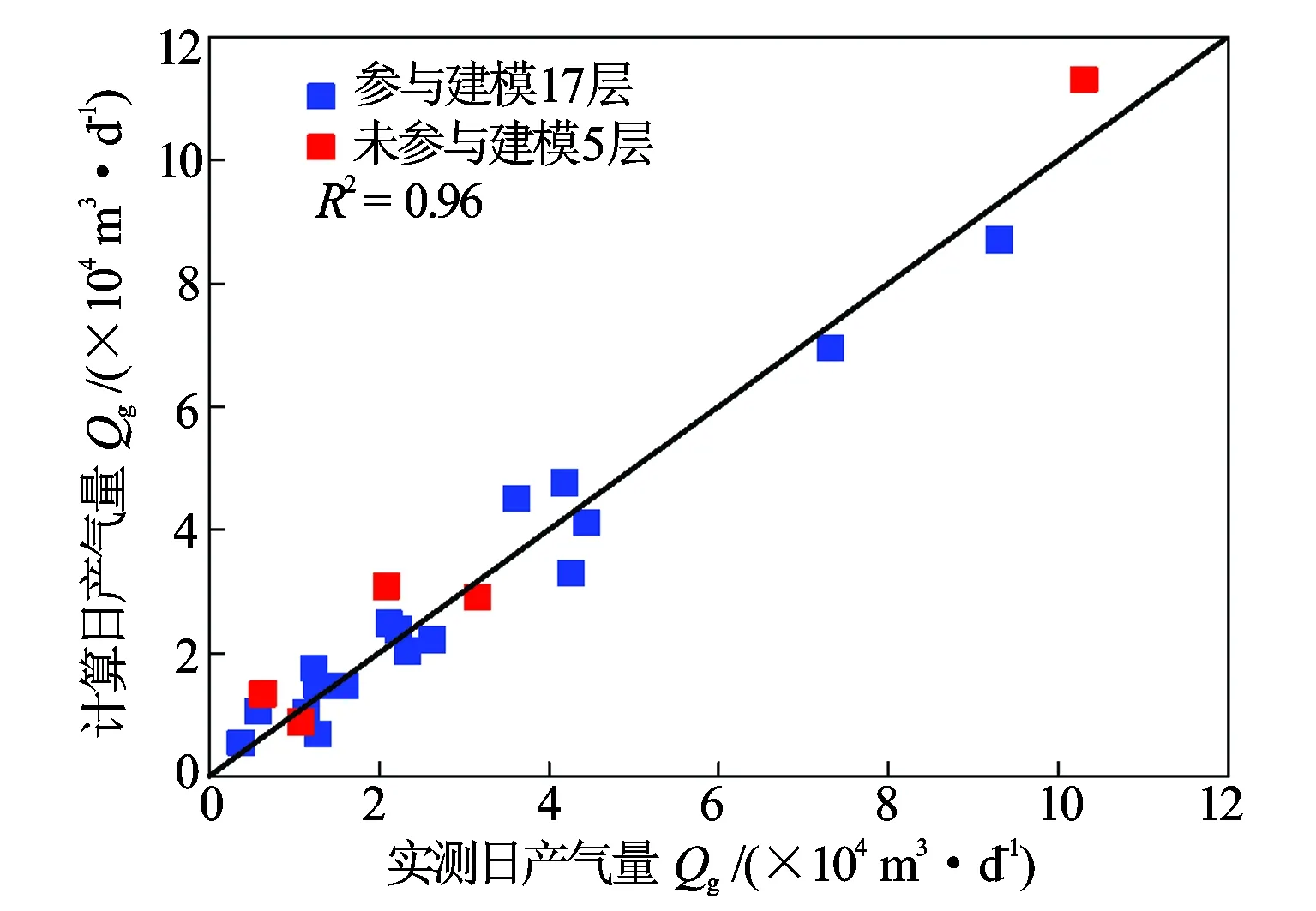
图8 实测产能与阵列声波预测产能交会图

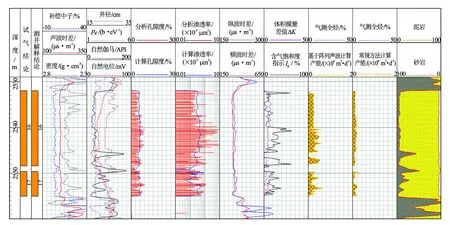
图9 A井产能预测效果图

3 效果分析

分别应用常规产能预测模型与基于阵列声波资料的产能预测模型对研究区块2口井资料进行处理。图9为A井2 529～2 560 m井气层产能预测效果图。该井段渗透率计算误差较大,其原因为孔隙结构复杂,呈双峰或三峰结构;该井段岩屑含量较高,非均质性强,孔渗关系复杂,导致应用孔渗回归计算渗透率精度低。因此,基于常规测井参数的产能预测模型效果差。该井16号气层与17号气层为Ⅰ类储层,常规预测模型误差分别为40.3%;基于阵列声波测井预测模型误差分别为14.9%,准确度大大提高,说明该方法能够降低参数计算精度低导致产能预测偏差大的问题,在致密砂岩气层有较好的应用效果(见表5)。

图10为B井2 530～2 600 m井段气层产能预测效果图。13号气层与15号气层为Ⅰ类储层,16号干层与17号差气层合试,分别为Ⅲ类储层和Ⅱ类储层,常规预测模型误差分别为25.2%、26.8%和17.3%;基于阵列声波测井预测模型误差分别为13.8%、6.0%和4.7%,预测效果优于常规方法(见表5)。

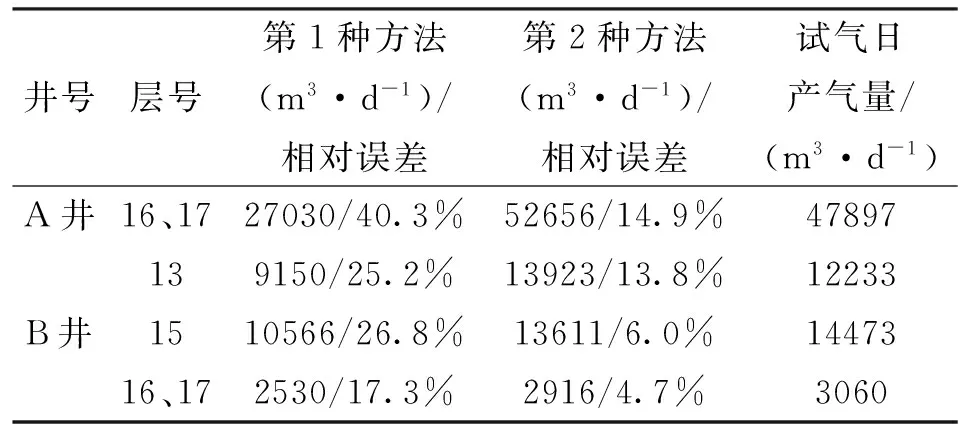
表5 不同方法产能预测结果对比表

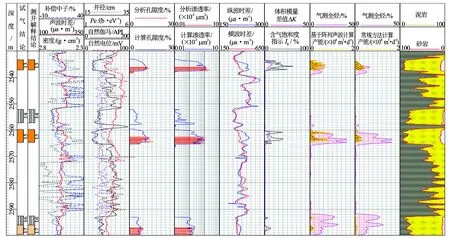
图10 B井产能预测效果图

4 结 论

(1) 在储层分类的基础上,利用常规测井资料,从渗流理论出发,建立产能预测模型,可实现产能快速预测,但对于致密砂岩气层,常规测井资料分辨率低,导致预测效果偏差较大。

(2) 基于岩石声学物理实验,研究了对储层含气性较为敏感的弹性参数,提出基于阵列声波测井资料的产能预测模型,大大提高了产能预测精度,在鄂尔多斯盆地东部上古生界致密砂岩气层产能预测取得较好的应用效果,并为含气性储层产能评价和预测的深入研究提供了一定的依据。

(3) 产能敏感参数的求取具有区域性和经验性,结合研究区特征,探索了基于Xu-White模型和Biot-Gassmann方程的敏感参数计算方法,效果较好。

参考文献:

[1] 邹才能, 陶士振, 袁选俊, 等. 连续型油气藏形成条件与分布特征 [J]. 石油学报, 2009, 30(3): 324-331.

[2] 杨华, 付金华, 刘新社, 等. 鄂尔多斯盆地上古生界致密气成藏条件与勘探开发 [J]. 石油勘探与开发, 2012, 39(3): 295-303.

[3] 韩雪, 潘保芝. 利用测井资料预测储层产能 [J]. 吉林大学学报: 地球科学版, 2010, 40: 102-105.

[4] 孙建孟, 运华云, 冯春珍. 测井产能预测方法与实例 [J]. 测井技术, 2012, 36(6): 628-634.

[5] 谭成仟, 马娜蕊, 苏超. 储层油气产能的预测模型和方法 [J]. 地球科学与环境学报, 2004, 26(2): 42-46.

[6] 成志刚, 张蕾, 赵建武, 等. 利用岩石声学特性评价致密砂岩储层含气性 [J]. 测井技术, 2013, 37(3): 253-257.

[7] 毛志强, 李进福. 油气层产能预测方法及模型 [J]. 石油学报, 2000, 21(5): 58-61.

[8] 张海涛, 石玉江, 张鹏, 等. 基于偶极横波测井的低

渗透砂岩气层识别方法 [J]. 测井技术, 2015, 39(5): 591-595.

[9] 范宜仁, 邢东辉, 邓少贵, 等. 低渗透岩石声学特征及在含气性预测中的应用 [J]. 西南石油大学学报: 自然科学版, 2015, 37: 64-70.

[10] Mavko G, Mukerji T, Dvorkin J. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media [M]. Cambridge: Cambridge University Press, 2009.

[11] Gassmann, F. Uber die Elastizitat Poroser Medien, Vierteljahrsschrift der Naturforschenden Gesellschaft in Zurich, 96: 1-23.

[12] Russell B H, Hedlin K, Hilterman F J, et al. Fluid-property Discrimination with AVO: A Biot-Gassmann Perspective [J]. Geophysics, 2003, 68(1): 29-39.

[13] Xu S, White R E. A New Velocity Model for Clay-sand Mixtures [J]. Geophysical Prospecting, 1995, 43(1): 91-118.

[14] Xu S, White R. Poro-elasticity of Clastic Rocks: A Unified Model [C]∥The SPWLA 36th Annual Logging Symposium, 1995.

[15] Key R G, Xu S. An Approximation for the Xu-White Velocity Model [J]. Geophysical, 1996, 67(5): 1406-1414.

[16] Biot M A. General Theory of Three-dimensional Consolidation [J]. Journal of Applied Physics, 1941, 12(2): 155-164.