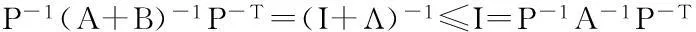异结构不等精度测量的融合估计分析

尹　晨，周海银，何章鸣

(国防科学技术大学理学院, 湖南 长沙 410073)



异结构不等精度测量的融合估计分析

尹晨，周海银，何章鸣

(国防科学技术大学理学院, 湖南 长沙 410073)

摘要：融合估计是提高参数估计精度的有效手段.针对异结构和不等精度测量条件，利用合同变换、迹函数和矩阵微分等数学工具，分析了融合估计问题.分析表明：第一，单设备估计、最优融合估计和联合估计都是融合估计的特例；第二，联合估计的精度高于低精度单设备估计的精度；第三，最优估计的精度高于高精度单设备估计的精度，而且总是高于联合估计的精度；第四，只有满足一定条件，联合估计的精度才高于高精度单设备估计的精度.上述理论在V2导弹参数融合估计的仿真中得到了验证.

关键词：参数估计；融合估计；联合估计；最优融合估计；合同变换；迹函数；矩阵微分

在众多参数估计领域中，融合估计是提高参数估计精度的有效手段[1-3].在实际靶场数据处理中，往往存在多台测量设备，不同设备的观测几何往往是不同的，即所谓的异结构测量；同时，不同设备的测量精度也是不同，即所谓的不等精度测量.由于设备的类型不同、采样周期的差异、设备位置的站址不同、周围气象的差异等原因，造成了设备的观测几何的差异，这个差异往往表现在设计矩阵上.异结构测量条件下，不同设备对应的基函数及其各阶导数都不同，因而对应的设计矩阵也不同.单测量设备精度差异主要是由设备的制造工艺的差别和设备测量人员的调校差异引起的.融合估计理论对靶场数据融合处理具有重要指导意义，为其提供了理论支撑[4,5].对于线性回归模型的参数估计，Gauss-Markov定理给出了不等精度测量数据的最优融合估计的加权因子计算方法[6].Gauss-Markov假设下，观测数据的随机误差是独立同分布[7-12]，然而不等精度测量条件下，不同设备的测量精度往往是不同的，而且这些精度参数往往是未知的，因此在实际数据处理过程中，难以得到最优融合估计[11,12,14-18]，从而经常用到的是联合估计(即等权估计).本文关注下面几个问题：第一，如何用统一的公式概括单设备估计、最优融合估计和联合估计？第二，单设备估计、最优融合估计和联合估计的估计精度存在什么关系？第三，在什么条件下，联合估计的估计精度高于单设备估计的精度？

1参数估计和精度分析

1.1线性模型和参数估计

考虑如下线性测量模型：

y=Xβ+e

(1)

模型(1)中参数β的最小二乘估计，如下：

(2)

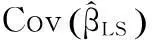
(3)

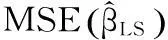
(4)

在靶场数据处理中，往往会出动多台设备对目标进行观测，本文不妨假设有两台设备，如下：

(5)

如果只使用其中的一台设备数据进行参数估计，那么单设备的参数估计的精度分别为：

(6)

记

(7)

其中λ称为测量精度比，下文总是假定：

(8)

1.2融合估计

若依据下述准则估计参数

(9)

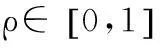
(10)

参数的融合估计如下：

(11)

容易验证

(12)

(13)

(14)

1.3特殊的融合估计

1.3.1单设备估计

若在优化准则(9)中ρ=1或者ρ=0，则融合估计转化为单设备参数估计.

依据附录A，可以证明

(15)

即融合估计的精度总是比低精度单台设备估计的精度高.

1.3.2最优融合估计

(16)

(17)

依据附录A，可以证明

(18)

即多台设备的最优估计的精度总是高于单台设备估计的精度，甚至比高精度单台设备估计的精度还要高.从信息论的观点来看，所有设备都蕴含了对参数估计有用的信息，因此，只要方法合适，就可以通过增加测量设备的方法提高参数估计的精度，即使增加的设备测量精度很低，也可以提高参数估计的精度.

1.3.3联合估计

(19)

(20)

依据附录B，可以证明

(21)

即多台设备的最优估计的精度总是高于多台设备的联合估计的精度，而且联合估计的精度总是高于低精度单台设备估计的精度，但是不一定高于高精度单台设备估计的精度，即下式成立需要一定的条件：

(22)

如果(22)式不成立，则说明低精度设备的参与使得参数估计的精度变差了，这意味着联合估计不如用单台高精度设备，下一节分析(22)式成立的条件.

2联合估计分析

若第一台设备的估计方差更小，即

(23)

由公式(6)、(7)、(20)可知，公式(22)与下式等价：

(24)

(25)

由公式(6)、(7)、(20)可知，公式(22)与下式等价：

(26)

2.1观测几何相同

如果两台设备的观测几何相同，即A=B，那么，公式(24)和(26)分别等价于

(27)

和

(28)

综上，若以下公式成立，则公式(22)成立

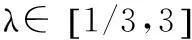
(29)

2.2观测几何不相同

如果两台设备的观测几何不相同，即A≠B，那么分两种情况讨论：

第一种情况下：公式(24)成立，则依据附录A，必然存在可逆矩阵P使得

(30)

(31)

即

(32)

第二种情况下：公式(25)成立，则依据附录A，必然存在可逆矩阵P使得

(33)

所以，若以下公式成立，则公式(24)成立

(34)

即

(35)

综合公式(32)和(35)得公式(24)成立的充分条件：

(36)

3仿真分析

本文以著名的德国V2弹道导弹为仿真对象，V2导弹垂直上升到24km～29km后，在发动机喷口燃气舵的作用下以40度的倾角弹道上升，一分钟后导弹飞到48km高度，速度达到5796km/h，发动机关闭，火箭靠惯性继续上升到97km，然后以3542km/h的速度大致沿抛物线自由下落，大约2.5分钟后击中目标.其中重力加速度为g=9.7ms-2.

4种融合估计策略下的参数估计方差见表1和图1.可以得到如下结论：

表1　四种融合估计的比较

图1　融合方差与加权因子关系

4结论

由于本文没有考虑系统建模误差，所以本文的理论还有待改进.比如，因为存在空气阻力、重力加速度变化和弹体自身抖动，致使导弹自由下落段的轨迹不是严格的抛物线.如果选用二次多项式基函数建模，必然存在系统建模误差.系统误差是如何影响融合估计的，尤其是如何影响联合估计的，是未来要研究的问题.

参考文献：

[1]Bar-Shalom Y, Chen H, Mallick M. One-step solution for the multi-step out of sequence measurement problem in tracking [J]. IEEE Transactions on Aerospace and Electronics Systems, 2004, (1): 27-37.

[2]Li X R, Vesselin P. A Survey of maneuvering target tracking-Part V: multiple-model methods [A]. Proceeding of SPIE Conference on Signal and Data Proceeding of Small Targets[C]. San Diego, CA, USA, 2003.

[3]Mazuelas S, Prieto J. Adaptive data fusion for wireless localization in harsh environments[J]. IEEE Transactions on Signal Processing, 2012, (4): 1585-1596.

[4]Wang Z M, Yi D Y. Measurement Data Modeling and Parameter Estimation [M]. CRC Press, 2011.

[5]Bar-Shalom Y, Li X R, Kirubarajan T. Estimation with Applications to Tracking and Navigation[M]. New York: Wiley, 2001.

[6]陈希孺, 王松桂. 近代回归分析[M]. 合肥: 安徽教育出版社, 1987.

[7]Saha R K. Effect of common process noise on two-track fusion [J]. Journal of Guidance, Control & Dynamics, 1996, (4): 829-835.

[8]Gan Q, Harris C J. Comparison of two measurement fusion methods for Kalman filter based multi-sensor data fusion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, (5): 273-280.

[9]Bates D M, Watts D G. 非线性回归分析及其应用[M]. 韦博成，万方焕，朱宏国,译.北京: 中国统计出版社, 1997.

[10]韦博成. 近代非线性回归分析[M]. 南京:东南大学出版社, 1989.

[11]Rick A, Brian B, Cliff T. Parameter estimation and inverse problems [EB/OL]. http://www.ees.nmt.edu/Geop/Classes/GEOP529/Docs/draft.pdf, 2003-03-24.

[12]Kaipio J P, Juntunen M. Deterministic regression smoothness priors TVAR modeling [A]. ICASSP’99 Proceedings of the Acoustics，Speech and Signal Processing [C]. IEEE，1999.

[13]Tikhonov A N. Solutions of Ill-Posed Problems [M]. New York: John Wiley & Sons, 1977.

[14]Voutilainen A, Stratmann F, Kaipio J P. A non-homogeneous regularization method for the estimation of narrow aerosol size distributions [J]. J Aerosol Sci, 2000, (4): 1433-1445.

[15]刘继军. 不适定问题的正则化方法及应用[M]. 北京：科学出版社，2005.

[16]Bronstein M M. Blind deconvolution of images using optimal sparse representations[J]. IEEE Transactions on Image Processing,2005,(6): 726-736.

[17]Kirsch A. An Introduction to the Mathematical Theory of Inverse Problems [M]. New York: Springer-Verlag, 1996.

[18]Poggio T, Torre V, Koch C. Computational vision and regularization theory [J]. Nature, 1985, (317): 314-319.

附录

附录A

已知：已知A和B都是n阶方阵，而且都是正定矩阵.

求证：tr(A+B)-1

证明：

第三步：因为(A+B)-1

附录B

已知：已知A和B都是n阶正定矩阵，λ>0.

求证：

tr(A+λ-1B)-1≤tr(A+λB)(A+B)-2

≤max{tr(A-1),λtr(B-1)}

证明：

第二步：记融合估计的方差为：

tr(ρ)

=tr(ρ2A+λ(1-ρ)2B)(ρA+(1-ρ)B)-2

显然有：

tr(ρ)

=trPT(ρ2I+(1-ρ)2λΛ)(ρI+(1-ρ)Λ)-2P-1

可知命题成立.

(责任编校：晴川)

Fusion Analysis on Estimation of Multi-structure and Unequal-precision

YIN Chen, ZHOU Haiyin, HE Zhangming

(College of Science, National University of Defense Technology, Changsha Hunan 410073, China)

Abstract：Fusion estimation is an effective measure to improve the precision of parameters estimation. In this paper, the fusion estimation problem is analyzed for the measurement conditions with multi-structures and unequal-precisions, using the tools of congruent transformation, trace function and matrix differential. Analysis shows that: Firstly, the single equipment estimation, the optimal fusion estimation and the joint estimation are some special cases of the fusion estimation; Secondly, the precision of the joint estimation is higher than that of the single equipment estimation with smaller random error; Thirdly, the precision of the optimal estimation is higher than that of the single equipment estimation with bigger random error, and is always higher than that of the joint estimation; Forthly, the precision of the joint estimation is higher than that of the single equipment estimation with bigger random error if certain conditions are satisfied. The fusion estimation theories results are validated by the simulation of the V2 missile.

Key Words：parameter estimation; fusion estimation; joint estimation; optimal fusion estimation; congruent transformation; trace function; matrix differential

中图分类号:O29

文献标识码：A

文章编号：1008-4681(2016)02-0009-04

作者简介：尹晨(1992— )，女，湖南衡阳人，国防科学技术大学理学院硕士生.研究方向：数据融合理论及应用、故障诊断理论及应用.

基金项目：国家重点基础研究项目(批准号：613156030103)；国家自然科学基金(批准号：61304119)资助项目；国防科大科研基金(批准号：JC14-09-01)资助项目.

收稿日期：2015-11-20