Diophantine方程x3-1=6Dy2的整数解
2016-05-06李润琪
李润琪
(德宏师范高等专科学校数学系, 云南 芒市 678400)
Diophantine方程x3-1=6Dy2的整数解
李润琪
(德宏师范高等专科学校数学系, 云南 芒市 678400)
摘要:设为奇素数,ri≡-1(mod6)(i=1,2,…,n)为彼此不相同的奇素数.运用同余式、平方剩余、Pell方程的解的性质、递归序列等讨论了Diophantine方程x3-1=6Dy2的整数解的情况.
关键词:Diophantine方程;整数解;同余;奇素数;递归序列;平方剩余
Diophantine方程x3+1=Dy2(D>0,D无平方因子,x,y∈Z)是一类基本而又重要的方程,当D含6k+1型素因子时,其整数解已有不少人研究过.当D不含素因子2和3时,文[1]已进行了一些研究;当D含素因子2,但不含素因子3时,文[2]已进行了一些
研究;当D含素因子3,但不含素因子2时,文[3]-[5]已进行了一些研究;当D既含素因子2,又含素因子 3时,文[5]已进行了一些研究.本文主要给出了D含素因子2,3,一个6k+1型素因子及至少一个6k-1型素因子时方程(1)的解的情况.
1引理
引理1[6]设r≡-1(mod6)为奇素数,(x,y)为x2-3y2=1的整数解,则x
≡
0(modr).
引理2[7]设p是一个奇素数,则丢番图方程x4-py2=1除开p=5,x=3,y=4和p=29,x=99,y=1820外,无其他的正整数解.
引理3[7]设p是一个奇素数,则丢番图方程4x4-py2=1除开p=3,x=y=1和p=7,x=2,y=3外,无其他的正整数解.
2定理及证明

x3-1=6Dy2
(1)
在下列条件下仅有平凡解(x,y)=(1,0):
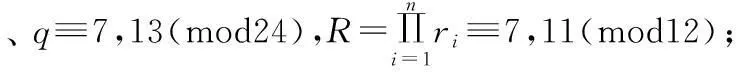
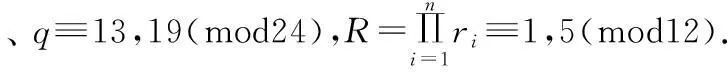
证明设(x,y)是方程(1)的整数解,因为x3-1=(x-1)(x2+x+1),而gcd(x-1,x2+x+1)=3.设x2+x+1≡0(modri)(i=1,2,…,n),即4x2+4x+4≡0(modri)(i=1,2,…,n),则有(2x+1)2+3≡0(modri)(i=1,2,…,n),即
(2x+1)2≡-3(modri)(i=1,2,…,n)
(2)
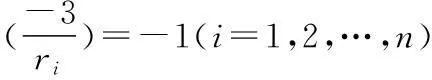
≡
0(modri)(i=1,2,…,n).又x2+x+1
≡
0(mod2),x2-x
+1
≡
0(mod9),故方程(1)给出下面2种可能的情形:
x-1=18u2R,x2+x+1=3qv2,y=3uv,gcd(u,v)=1
(3)
x-1=18Du2,x2+x+1=3v2,y=3uv,gcd(u,v)=1
(4)
由(3)式的x-1=18u2R,得x=18u2R+1≡2u2R+1(mod8).又u2≡0,1,4(mod8),则x≡2u2R+1≡1,2R+1(mod8).又由(3)式的x2+x+1=3qv2及q为奇素数知v为奇数,则v2≡1(mod8).
综上有(3)式不成立.
由(4)式的x2+x+1=3v2得(2x+1)2+3=12v2,将(4)式的x-1=18Du2代入得
(36Du2+3)2+3=12v2,即(12Du2+1)2+1=4v2=(2v)2,移项得
(2v)2-3(12Du2+1)2=1
(5)

因此有12Du2+1=±yn(n∈Z),即有12Du2=±yn-1.又因为y-n=-yn,所以只需考虑下式:
12Du2=yn-1.
(6)
由(6)式得yn≡1(mod12).
容易验证下列各式成立:
yn+2=4yn+1-yn,y0=0,y1=1
(7)
yn+1=xn+2yn
(8)
(9)
x2n=2xnyn
(10)
xn+1=2xn+3yn
(11)
x2n+1≡2(mod4),x2n≡1(mod2)
(12)
x2n+1≡2(mod3),x2n≡1(mod3)
(13)
y2n+1≡1(mod2),y2n≡0(mod4)
(14)
xn+2=4xn+1-xn,x0=1,x1=2
(15)
对递归序列(7)取模12,得周期为12的剩余类序列0,1,4,3,8,5,0,7,4,9,8,11, 0,1,4,3,…,
且当且仅当n≡1(mod12),有yn≡1(mod12),所以(6)式要成立必需满足n≡1(mod12).

6Du2=x6m+1y6m
(16)
由(11)式及(14)式得,gcd(x6m+1,y6m)=gcd(2x6m+3y6m,y6m)=gcd(2x6m,y6m)=gcd(2,y6m)=2.因为ri≡-1(mod6)(i=1,2,…,n)是彼此不相同的奇素数,故由引理1知x6m+1
≡
0(modri)(i=1,2,…,n).又由(12)式得x6m+1≡2(mod4),则有2||x6m+1.
又由(13)式得x6m+1
≡
0(mod3),由(14)式得y6m≡0(mod4).所以(16)式给出以下2种可能的情形:
x6m+1=2qa2,y6m=12Rb2,u=2ab,gcd(a,b)=1
(17)
x6m+1=2a2,y6m=12Db2,u=2ab,gcd(a,b)=1
(18)
由(17)式的y6m=12Rb2及(10)式可得2x3my3m=12Rb2,则有x3my3m=6Rb2.因为ri≡-1(mod6)(i=1,2,…,n)是彼此不相同的奇素数,故由引理1知x3m
≡
0(modpi)
(i=1,2,…,n).又由(13)式得x3m
≡
0(mod3),而且gcd(x3m,y3m)=1,故y6m=12Rb2可以分解为以下两种可能的情形 :
x3m=c2,y3m=6Rd2,b=cd,gcd(c,d)=1
(19)
x3m=2c2,y3m=3Rd2,b=cd,gcd(c,d)=1
(20)
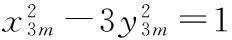
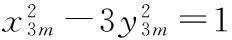

综上有(18)式给出方程(1)仅有平凡解(x,y)=(1,0).
参考文献:
[1] 杜先存,万飞,赵金娥.关于丢番图方程[J].安徽大学学报:自然科学版,2014,(2):23-26.
[2] 杜先存,赵东晋,赵金娥.关于不定方程[J].曲阜师范大学学报:自然科学版,2013,(1):42-43.
[3] 杜先存.关于丢番图方程的整数解[J].郑州大学学报:理学版,2015,(1):38-41,45.
[4] 万飞,杜先存.关于Diophantine方程[J].唐山师范学院学报,2014,(2):14-15.
[5] 杜先存,孙映成,万飞.关于丢番图方程x3±1=3·2αpD1y2[J].数学的实践与认识,2014,(6):255-258.
[6] 杜先存.关于不定方程的整数解的研究[J].浙江大学学报:理学版, 2014,(2):96-99.
[7] 曹珍富.丢番图方程引论[M].哈尔滨:哈尔滨工业大学出版社,2012.
(责任编校:晴川)
Integer Solutions of Diophantine Equationx3-1=6Dy2
LI Runqi
(College of Mathematics, Dehong Normal College, Mangshi Yunnan 678400, China)
Abstract:Let ri(n∈Z+),q≡1(mod6)be odd prime and ri≡-1(mod6)(i=1,2,…,n) be different odd primes. The integer solutions of the equation in title are discussed with the help of congruence, quadratic remainder, some properties of the solutions to Pell equation and recursive sequence.
Key Words:Diophantine equation; integer solution; congruence; odd prime; recursive sequence; quadratic remainder
中图分类号:O156.1
文献标识码:A
文章编号:1008-4681(2016)02-0006-03
作者简介:李润琪(1965— ),男,云南腾冲人,德宏师范高等专科学校数学系讲师.研究方向:初等数论、数学教育.
基金项目:云南省教育厅科学研究项目(批准号:2014Y462).
收稿日期:2015-10-25
