电力大客户负荷模式研究

罗煜

摘 要：在当前国家推进电力市场化交易的形势下，研究电力大客户的负荷模式具有重要意义。文章通过应用K-means的聚类算法，实现对工业大客户的电力负荷模式识别。同时，也提出了通过小波的方法压缩存储空间，并简要分析了负荷模式对负荷预测的作用。

关键词：负荷模式；K-means聚类；负荷预测

中图分类号：TM714 文献标识码：A 文章编号：1006-8937（2016）12-0117-03

许多企业用户对电力的需求相当大，这些电力大客户日负荷非常大，并且其负荷模式常常在一段时期内基本固定。

本文通过K-means的聚类算法对其日负荷曲线进行模式识别，来研究电力大客户的负荷模式。通过对电力大客户的负荷模式研究，可以大致掌握其用电规律，并可应用于负荷预测、需求侧响应、调度管理等实际工作中。

1 电力负荷模式研究

1.1 测度函数

在进行电力客户模式研究时，必须先定义近邻测度函数。近邻测度函数有两种，一种是相似性测度，两个向量（或点集）之间越相似，其相似测度函数值越大；另一种是不相似测度，两个向量（或点集）之间越相似，其不相似测度函数值越小。

著名的欧氏距离函数即是一种不相似性测度函数，对两个向量x，y而言，其欧氏距离定义为：

d■=（x，y）=■2■（1）

在本文中，采取常用的一种相似性测度函数Pearson系数来衡量日负荷曲线间的相似性。Pearson系数定义为：

rPearson（x，y）=■（2）

1.2 负荷曲线去噪

对于电力负荷曲线而言，我们更关心的是曲线的整体形状，局部的“毛刺”对曲线的整体形状影响不大。为了聚类结果更快速，以及节省储存空间，这里提出用Haar小波去燥的方法来处理负荷曲线。

Haar小波的尺度函数定义为：

φ（x）=1， 若0≤x<10， 其余情况（3）

？撞k∈zφ（2jx-k）构成一组正交基，其正交补定义为：

？撞k∈z？渍（2jx-l）

？渍（x）定义如下：

？渍（x）=1， 若0≤x≤1/2-1， 若1/2≤x<1 0， 其余情况（4）

将日负荷曲线展开为？渍（2jx-l）与φ（x-k）的序列相加，去掉属于较大的j的？渍（2jx-l）分量（去噪），但如果？渍（2jx-l）前的系数很大则予以保留，再进行重构。

1.3 聚类算法

对负荷曲线进行聚类就是把大量负荷曲线分割成不同的类，使得同一个类内的负荷曲线的相似性尽可能大，同时不在同一个类中的负荷曲线的差异性也尽可能地大。即聚类后相似的负荷曲线尽可能聚集到一起，不同负荷曲线尽量分离。 K-means聚类算法是经典的聚类1之一。其聚类准则采用平方误差准则，其定义如下：

E=■■f■（p，m■）（5）

式中，E的值是聚类的判断条件，p为需要聚类的元素，Ci为一个类，mi为Ci的中心。ki为Ci目前的元素数目，f为测度函数，表示元素p到mi的距离，本文采取f=■。其聚类算法过程如下：

①设共有x个元素，目前已有个n元素已聚类，目前有m个类Ci（i=1，2，…，m），Ci的元素个数为ki设定阀值？夼。

②对第n+1个元素pn+1，对于每个类Ci，求取将pn+1归并入Ci后的Ei，取最小的Ei为Emin，设此时i=o，若Emin<？夼，则将pn+1归入Co中，否则新建一个类Cm+1={pn+1}。

③重复步骤①②，直到n=x，所有元素聚类为止。

1.4 实际数据分析

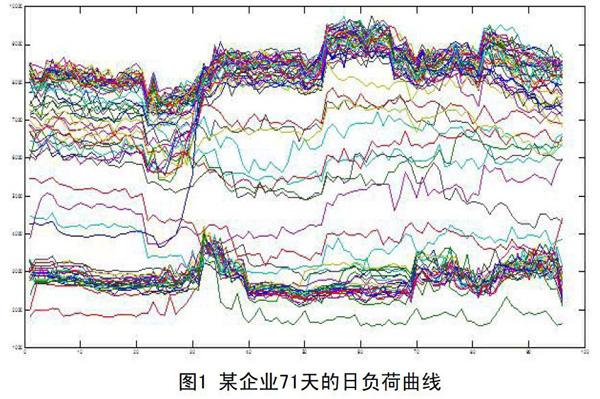
以下为某企业连续71 d的日负荷曲线（每15 min采样一次，单条日负荷曲线共96个数据点），如图1所示。

采用1.3的聚类算法，得到的结果，如图2所示。

2 电力客户负荷预测的应用

大型制造型企业在一段較短时间内负荷模式基本不变。因此，对于用电量较大的电力客户，可以采取负荷模式来进行负荷预测。

从图1中挑选出连续8 d的日负荷曲线，如图3所示。

通过聚类算法后，其中一条明显不同与其他的负荷曲线被区分出来，得到的结果，如图4（a）（b）所示。该条明显不同的负荷曲线其实是对应企业的某个周日的负荷曲线。

另外，图3采用Harr小波去噪后，得到的结果，如图5所示。对图5的曲线采用同样的聚类算法，和图4的聚类结果相同，但聚类过程中其相关性变得更明显，而且图5每条负荷曲线只有48个数据点，比图4的节省了一般储存空间。

从图4中a类取3条连续的日负荷曲线，如图6所示，我们假想下一天的负荷模式与（a）类相同。

然后，我们可以用选取的这三条日负荷曲线，经过小波去燥后，如图7所示，求出其中心曲线，如图8所示。这里我们把中心定义为图7中三条曲线相加后求平均，中心的定义也可以参考聚类算法中的一些经典定义。

我们将第4日的日负荷曲线与中心曲线放相对比得到的结果，如图9所示。通过计算，其Pearson相关系数系数达到0.9667，可见，电力负荷模式识别对负荷预测有极其重要的作用。

3 结 语

本文通过应用K-means的聚类算法将电力大客户的日负荷曲线进行聚类，研究其负荷模式。本文分析表明，K-means聚类算法对负荷曲线聚类有很好的效果。同时，负荷模式对于分析电力客户的用电行为及其负荷预测有重要作用。在目前推进电力市场化交易的背景下，大客户的电力负荷模式研究具有重要意义。如何进一步采取数据挖掘等方法和手段去更深入了解用户行为去指导实际工作等课题，需要进一步展开研究。

参考文献：

[1] 西奥多里蒂斯.李晶皎（译）.模式识别（第四版）[M].北京：电子工业出版 社，2012.

[2] 刘耀年.基于模糊识别与模糊聚类理论的短期负荷预测[J].电工技术 学报，2002，（5）.

[3] 许甜田.大用户负荷预测方法研究及其应用[D].长沙：湖南大学，2013.

[4] Jiawei Han，Micheline Kamber.数据挖掘概念与技术[M].北京：机械工 业出版社，2007.

[5] 刘丽轻.电力用户负荷模式识别系统研究与设计[D].北京：华北电力大 学，2011.

[6] 张忠华.电力系统负荷分类研究[D].天津：天津大学，2007.

[7] Kuncheva，L. L，Vetrov， etal.Evaluation of Stability of k-Means ClusterEnsembles with Respect to Random Initialization [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2006，（11）.

[8] Shehroz S. Kha，Amir Ahmad. Cluster center initialization algorithmfor K-means clustering[J]. Pattern Recognition Letters，2004.

[9] 仲伟宽.模糊聚类方法在用户负荷曲线分析中的应用[J].华东电力，2007，（8）.