求解TSP问题的改进最邻近法

赖志柱，戈冬梅，张云艳（1.贵州工程应用技术学院a.理学院；b.生态工程学院，贵州毕节551700）



求解TSP问题的改进最邻近法

赖志柱1a，戈冬梅1b，张云艳1a
（1.贵州工程应用技术学院a.理学院；b.生态工程学院，贵州毕节551700）

摘要：考察TSP问题的线路构造，建立TSP问题的数学模型，分析了最邻近法的基本思想及不足，通过改进最邻近法构造线路的方向及将所有城市均作为一次线路构造的起点，提出了双向最邻近法、完全最邻近法和完全双向最邻近法三种改进方法，算例表明改进后的方法比最邻近法能获得更多的不同线路及更优的线路。

关键词：TSP问题；最邻近法；线路

1引言

旅行商问题（Traveling Salesman Problem,TSP），也称为旅行推销员问题或货郎担问题，是运筹学、图论以及组合优化中的著名难题，由于其应用的广泛性，引起了人们的极大的兴趣。TSP问题的解决方法可以直接或较容易地应用于解决类似的问题，如交通车辆的巡回线路问题、民航机组人员的轮班安排问题、教师任课班级负荷分配问题、装配线进度问题等。该问题的求解算法主要分为两类：与问题特征相关的启发式搜索算法[1][2]（如动态规划法、分支定界法等）以及独立于问题的智能优化算法[3][4]（如遗传算法、模拟退火算法等）。通常，将TSP问题的启发式方法分为线路构造法、线路改进法和综合法三类[5]，最邻近法是线路构造法中最简单的一种，但该方法对于城市规模较大的TSP问题求解效果较差，本文拟就最邻近法做些改进，以期改进后的方法在线路构造中能给出更优的结果以及对规模较大的TSP问题也有较好的效果。

2 TSP问题的描述及数学模型

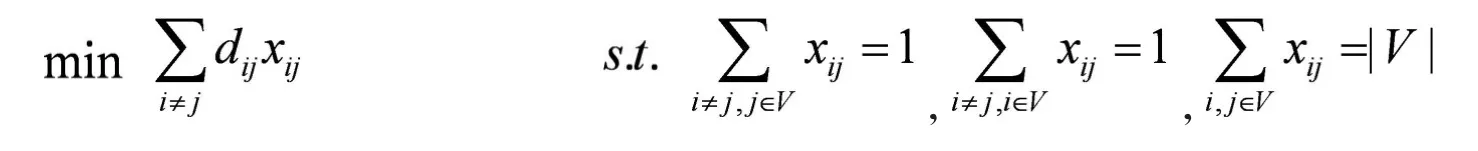
3最邻近法的改进

3.1最邻近法简述及分析

求解TSP问题的最邻近法（NearestNeighbor，NN）的基本思想可以简述为：给定源点作为线路的起点，寻找并加入距离上一次加入线路中顶点（城市）最近的顶点（城市），依次重复直到所有顶点（城市）已经加入线路，最后将源点加入到线路末尾即可。

显然该方法的本质是贪心策略（以距离上一次加入的顶点最近的点为策略）在线路中的具体实现，由于贪心算法在复杂问题中未必能得到最优解，因而该方法通常不能得到问题真正的最优路径，但胜在直观和速度较快。在使用最邻近法寻找TSP的线路时，也存在一些疑难或问题，例如，最邻近法在选定哪一个城市作为源点上并没有标准；另一方面，当线路寻找过程中如果有两条子路径长度一样，如何选择新的子路径，最邻近法也没有给出明确的做法。在实践中，笔者发现选择源点不同，最邻近法获得的最优线路也有所不同；有时即使源点选择相同，但寻路中间如果有长度相同的子路径，此时选择的方式不同也会有差异。下面以一个例子[5]说明，该问题共有8个城市，具体数据如表1。

表1　8个城市间的距离数据

文献利用最邻近法得到的线路为1-3-7-8-6-2-4-5-1，线路总长度为62。分析最邻近法获得的线路，当将城市1和3加入线路后，距离城市3最近的城市有两个（4和7），如果此时不选择城市7而选择城市4加入线路中，则可得到另一条线路：1-3-4-5-7-8-6-2-1，总长度为54。若将城市2作为源点，则可得到两条线路：（1）线路1长度为66，表示为2-6-7-8-3-1-4-5-2；（2）线路2长度为61，表示为2-6-8-7-3-1-4-5-2。

3.2改进1：双向最邻近法

这种改进是将最邻近法中寻找下一个城市的单一方向变化为两个方向同时寻找，具体步骤如下：

算法：双向最邻近法（Both-side NearestNeighbor，BSNN）

Step 1：选定一个城市作为源点，将该点加入线路中，以RightC表示右前方刚加入的城市，以LeftC表示左后方刚加入的城市，此时RightC=LeftC=源点。

Step 2：查找还未加入线路且距离RightC最近的一个城市RC，更新RightC=RC及线路信息；查找还未加入线路且距离LeftC最近的一个城市LC，更新LeftC=LC及线路信息。

Step 3：检查剩下的还未加入线路的城市个数，若剩下的城市个数大于2，转Step 2；若剩下一个城市，则直接将剩下的城市作为RightC加入线路；若还剩下两个城市（记为C1和C2），若C1比C2距离RightC更近，则赋值RightC=C1及LeftC=C2，否则RightC=C2，LeftC=C1。

Step 4：将RightC与LeftC之间的子路径加入线路，输出获得的线路。

3.3改进2：完全最邻近法

由2.1的分析可知，最邻近法获得的结果总是差强人意，为得到较优的结果，对最邻近法改进得到完全最邻近法（Complete NearestNeighbor，CNN），具体做法为：依次对每一个顶点（城市）执行最邻近法搜索，汇总所有获得的TSP线路，将重复的线路删除，最后对剩下的线路依据长度进行排序。

3.4改进3：完全双向最邻近法

有时利用双向最邻近法获得的TSP线路效果不是很理想，仿照完全最邻近法的做法，对双向最邻近法改进得到完全双向最邻近法（Complete Both-side NearestNeighbor，CBSNN），具体做法为：依次对每一个顶点（城市）执行双向最邻近法搜索，汇总所有获得的TSP线路，将重复的线路删除，最后对剩下的线路依据长度进行排序。

4算例及结果

为检验最邻近法及其三种改进的效果，分别基于MATLAB 7.1编制程序，首先以表1中8个城市的数据运行，结果如表2。由于最邻近法的结果可从完全最邻近法的结果中查找，而双向最邻近法的结果也可从完全双向最邻近法的结果中查找，故表2仅列出了完全最邻近法及完全双边最邻近法的结果；另外，为便于线路对比，所有线路最后都转化为从顶点（城市）1出发，最后都回到顶点（城市）1。从表2可看出，改进后的三种方法，尤其是完全最邻近法及完全双边最邻近法，不比原来的最邻近法效果差，而且总是能得到TSP问题的众多不同线路，从而可在后续的研究或实践中使用其它算法（如遗传算法、蚁群算法等智能算法进一步优化获得最佳解）。另外，由于完全双向最邻近法使用的两个方向同时寻找，可以获得比完全最邻近法更多的不同线路，从而在使用智能算法后续优化中更具优势。

表2　完全最邻近法及完全双边最邻近法的结果

其次，以TSP问题中经典的kroal100数据（含100个城市）为例进行运算，四种算法的结果如表3所示。表3中，最邻近法NN和双边最邻近法BSNN仅给出了原始起点为顶点（城市）1时的结果，从结果可以看出BSNN的效果明显优于NN（25413.38<26856.39）；而CNN总共获得97条不同的线路，CBSNN总共获得99条不同的线路，限于篇幅都仅给出前8条较短的不同线路，从结果可看出，CBSNN的效果明显优于CNN（24510.75<24698）。详细对比CNN和CBSNN的前8条较短的不同线路，CBSNN的前3条较短线路都比CNN获得最短路更短，且CNN获得第二短的线路都比CBSNN的第8短线路还长。

表3　四种算法求解kroal100的部分结果

5结论与讨论

最邻近法是构造TSP线路的一种简单方法，其效果差强人意，尤其是对于规模较大的TSP问题，如kroal100。文章提出的双向最邻近法从两个方向同时构造线路，其效果明显优于最邻近法。当对所有顶点（城市）执行最邻近法及双向最邻近法（即文章提出的CNN和CBSNN）时，既可以获得众多的不同线路，也能获得比最邻近法和双向最邻近法都较好的线路，而且可以将获得众多的不同线路作为后续智能算法继续优化时的初始群体，这样既可以弥补随机生成线路的不足，又可以减少智能算法中群体规模的参数设置。

参考文献：

[1]杨忠程,徐新黎,叶双挺.基于组合拆分策略求解TSP的动态规划算法[J].计算机工程,2012(13):185-187,191.

[2]余文飞,郑鹏.分枝限界法的实现及改进方案[J].计算机应用与软件,2003(12):99-101.

[3]王剑文,戴光明,谢柏桥,等.求解TSP问题算法综述[J].计算机工程与科学,2008(2):72-74,155.

[4]潘正君,康立山,陈毓屏.演化计算[M].北京:清华大学出版社,1997.

[5]李军,郭耀煌.物流配送车辆优化调度理论与方法[M].北京:中国物资出版社,2001:6.

（责编：郎禹责校：明茂修）

ImprovedNearestNeighborMethodforSolvingTSP

LAIZhi-zhu1a,GEDong-mei1b,ZHANGYun-yan1a
(1a.SchoolofScience,1b.SchoolofEcologicalEngineering,GuizhouUniversityofEngineeringScience,Bijie,Guizhou551700,China)

Abstract:TodesignthepathofTSP,weestablishthemathematicalmodelandanalyzethenearestneigh⁃bormethod,andthenproposethreeimprovedmethods,whichcalledboth-sidenearestneighbormethod,com⁃pletenearestneighbormethodandcompleteboth-sidenearestneighbormethod.Atlast,someexamplesare givingandtheresultsshowthattheimprovedmethodsarebetterthanthenearestneighbormethod.

Keywords:TSPProblem;NearestNeighborMethod;Path

作者简介：赖志柱（1980-），男，江西赣州人，贵州工程应用技术学院理学院副教授。研究方向：智能算法及其应用、多式联运。

基金项目：贵州省科技厅、毕节市科技局、毕节学院科技联合基金项目“百里杜鹃旅游开发与生态环境协调机制模拟”，项目编号：黔科合J字LKB[2012]23号；贵州省科技厅、毕节市科技局、毕节学院科技联合基金项目“对两类椭圆方程解的理论研究”，项目编号：黔科合J字LKB[2013]24号；贵州省科技厅、毕节市科技局、贵州工程应用技术学院科技联合基金项目“车辆调度运输多目标模型及智能算法优化研究”，项目编号：黔科合LH字[2014]7532号。

收稿日期：2015-09-25

中图分类号：TP301.6

文献标识码：A

文章编号：2096-0239（2016）01-0139-04