并网逆变器的分裂电容无源阻尼设计与控制
2016-05-05于仲安
刘 莹,于仲安,邹 浩
(江西理工大学 电气工程与自动化学院,江西 赣州 341000)
并网逆变器的分裂电容无源阻尼设计与控制
刘莹,于仲安,邹浩
(江西理工大学 电气工程与自动化学院,江西 赣州 341000)
摘要:针对电感电容电感(loop capacitor loop,LCL)滤波的三相并网逆变器控制存在的谐振问题,结合分裂电容和无源阻尼两种方法,提出了分裂电容无源阻尼方案以及参数设计方法。首先,比较分析了分裂电容无源阻尼方案和完全电容阻尼方案之间的能量损耗与分裂电容容值比的关系;其次,分析了不同频率下能量损耗与分裂电容容值比的关系,使分裂电容容值比参数得到了进一步的优化。通过建立的MATLAB/Simulink仿真模型验证了该参数设计能够更有效地抑制谐振问题,降低并网电流总谐波畸变率和能量损耗,提高了系统的稳定性和动态性。
关键词:三相并网逆变器;LCL滤波器;分裂电容;无源阻尼
0引言
三相并网逆变器中,开关器件是电网最主要的谐波污染源。为了减少谐波污染,文献[1]在逆变器和电网之间加入电感电容电感(loop capacitor loop,LCL)滤波器。LCL滤波器与传统的L型滤波器相比,具有电流动态性能高、电感材料少和装置体积小等优点。但是 LCL滤波器自身存在一个零阻抗谐振点,导致系统稳定性差,所以必须采取有效措施抑制谐振来保证系统的稳定性[2-3]。对此,主要提出了两种解决方法:有源阻尼法和无源阻尼法[4-5]。有源阻尼法主要是通过增加传感器的数量和算法复杂度来抑制谐振,算法设计比较繁杂。而传统的无源阻尼法是在电容支路上串联无源电阻,方法简单可靠,系统稳定性好,但是系统的功率损耗较大。文献[6]提出了分裂电容法,此方法可以将控制系统由三阶系统降为一阶系统,保证系统的稳态和动态性能。文献[7]提出了分裂电容无源阻尼控制,将电容分裂成相等的两部分,在电网附近电容上串联小电阻,以降低系统损耗,并抑制LCL谐振现象。但是文献[7]的方法在滤除并网电流谐波含量方面没有取得很好的效果,却使分裂电容阻尼方案下的网侧电流总谐波畸变率(total harmonic distortion,THD)有所增加,并且这个方案设计不够全面,没有分析系统损耗与分裂电容容值比的关系。
本文提出了较为全面的分裂电容无源阻尼方案设计方法。从多个角度分析系统损耗与分裂电容容值比的关系,并在此基础上选择最优的分裂电容容值比。最后,在MATLAB/Simulink上建立分裂电容LCL滤波的三相逆变仿真模型,验证了该设计方案的正确性和有效性。
1LCL滤波器的数学模型
图1为带LCL滤波器的三相并网逆变器的主电路拓扑结构[8]。图1中:LCL滤波器由网侧电感Ls、逆变器侧电感Li和滤波电容Cf组成;ii为逆变器输出相电流;is为网侧输入相电流;us为电网相电压;udc为直流母线电压;Cdc为直流母线侧电容;uC为滤波电容电压;iC为滤波电容电流;S1~S6为逆变器开关管。
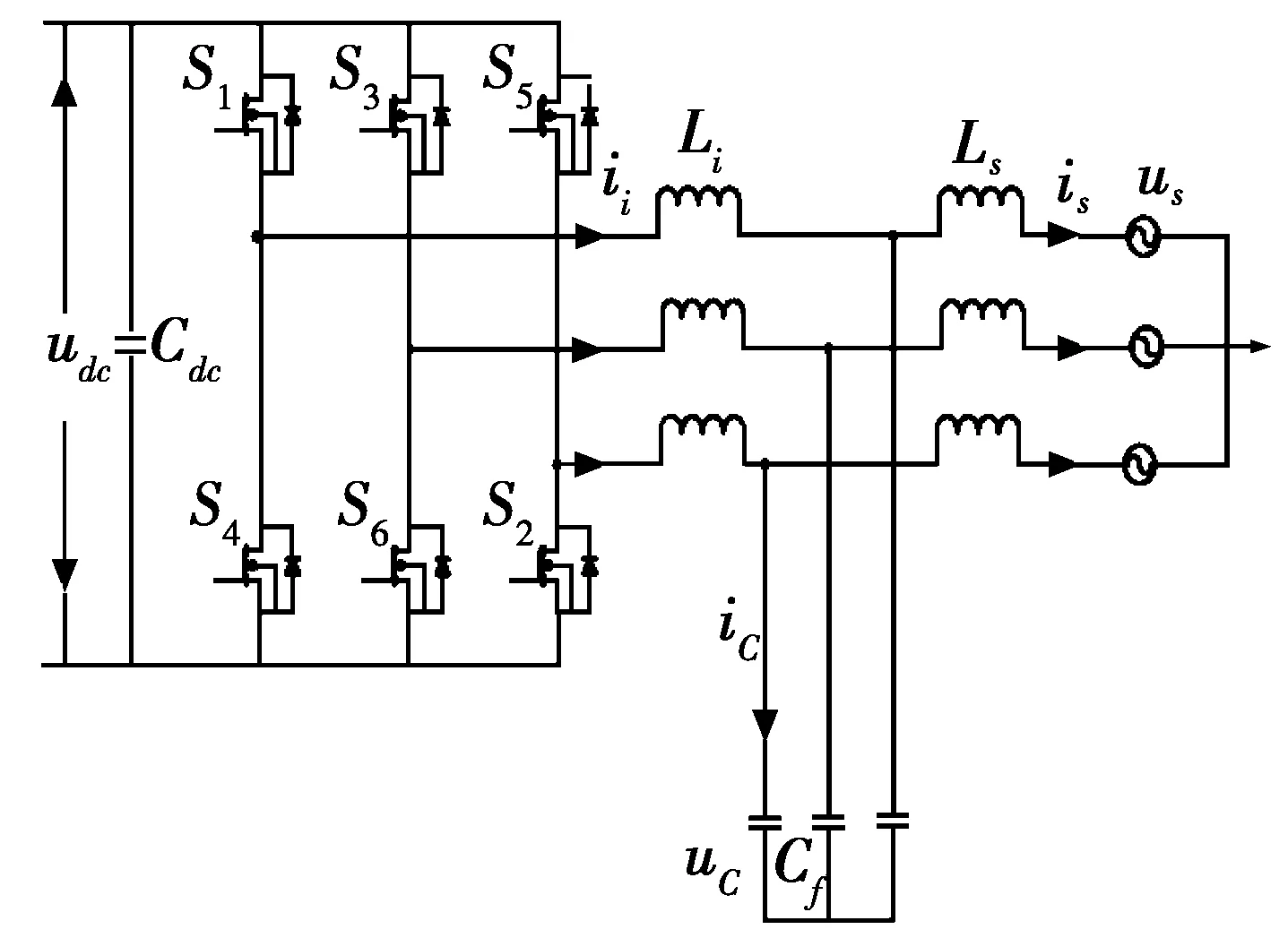
图1 三相并网逆变器的主电路拓扑结构图
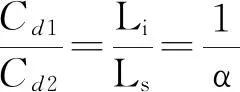
由图2可得出完全电容无源阻尼方案的LCL滤波器的传递函数为:
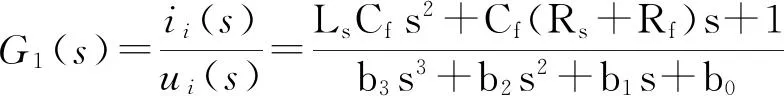
(1)
其中:b3=LsLiCf;b2=(LsRi+LiRs)Cf+(Ls+Li)RfCf;b1=(Rs+Ri)RfCf+Ls+Li+RsRiCf;b0=Rs+Ri。
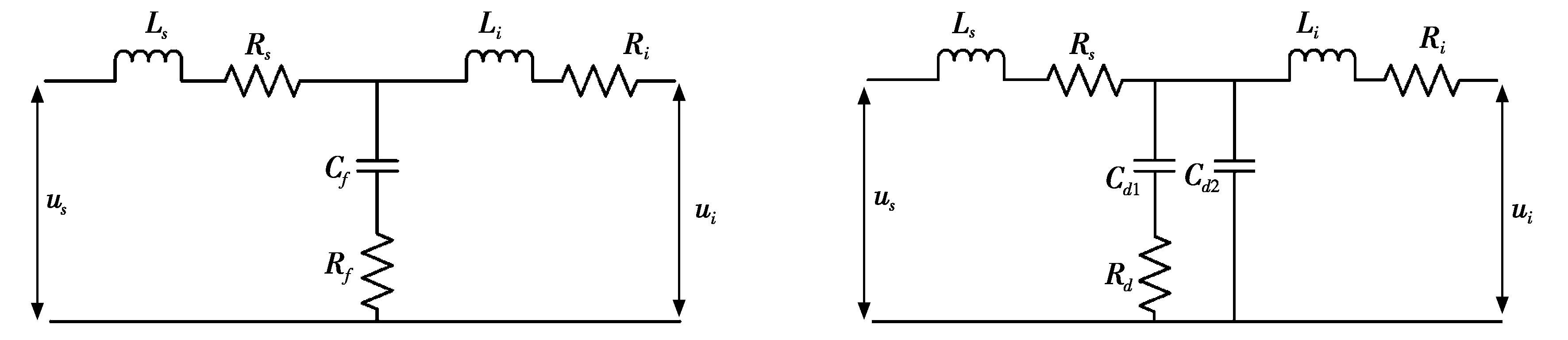
图2完全电容无源阻尼LCL滤波器单相等效电路图图3分裂电容无源阻尼LCL滤波器单相等效电路图
由图3可得出分裂电容无源阻尼方案的LCL滤波器的传递函数为:
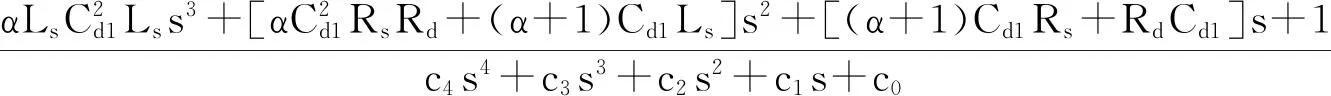
(2)

2分裂电容无源阻尼优化设计
2.1滤波器的主要参数设计
(Ⅰ)按允许的最大电流纹波指标和实现系统四象限运行,LCL滤波器总电感LT取值应满足下式[9-12]:
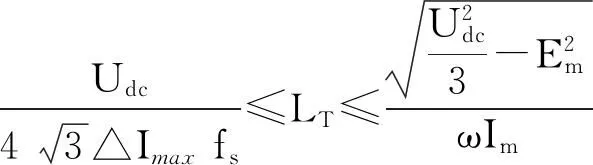
(3)
其中:△Imax为最大电流纹波值,数值为相电流峰值的1/10;fs为开关频率;Udc为直流母线电压;Im和Em分别为电网相电流峰值和相电压峰值;ω为电网角频率。
由式(3)得出满足系统要求的总电感的取值范围。为了提高系统的响应速度和电流的跟踪效果,并保证有较好的滤波效果,LT取较小值。
(Ⅱ)在滤波电容的容值设计上,电路要求该滤波电容吸收的基波无功功率小于或等于系统额定有功功率的5%,这样可以避免逆变器的功率因数太低。适当地增大电容容值可以降低总电感的感值,从而节约电感磁芯材料,降低成本。电容Cf的取值[11-12]为:
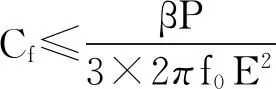
(4)
式中:P为变流器额定有功功率;β为基波无功功率与有功功率的比值,数值为5%;f0为电网频率;E为电网相电压有效值。
利用上述参数设计方法,对滤波器的电感电容进行设计。逆变器系统参数为:额定有功功率P=300 kW;电网线电压有效值E1=690 V;直流母线电压Udc=1 100 V;开关频率fs=2 kHz;相电流峰值Im=355 A。可得:LT=0.6 mH,Cf=167 μF。
2.2分裂电容法无源阻尼方案的选择
分析分裂电容无源阻尼电阻的功率损耗,确定分裂电容法所分裂的两个电容的容值比。由于电感比值与电容比值相等,故容值比的选择即是对电感比值α的选择。由分析分裂电容和完全阻尼方案的电阻损耗比来确定阻尼方案。
完全电容无源阻尼方案中阻尼电阻Rf的取值[7]为:
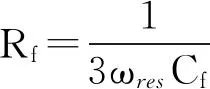
(5)
其中:ωres为谐振角频率。
由式(5)得出完全电容无源阻尼方案的电阻值为0.235 Ω。根据完全电容法和分裂电容法无源阻尼方案的滤除谐振效果一致,即式(1)和式(2)相等,并且忽略式(2)分母中的s4项和分子中的s3项的系数,可得Rd=(α+1)Rf。由于在计算时忽略了分母项,为了取得同样的滤波效果,Rd略微增大。
完全电容阻尼方案与分裂电容阻尼方案的电阻消耗的功率比值λ为:
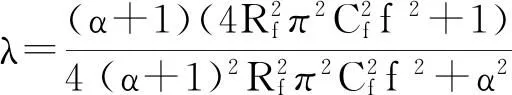
(6)
分析式(6)可得:两种方案的功耗比是由频率、电感比值和阻尼电阻共同决定的。在阻尼电阻的取值一定的情况下,主要分析频率和电感比值对两个方案的功耗比的作用,并综合得出最小功耗下的电感比值α。
根据λ的求取公式,得出电感比值与功率损耗的关系,如图4所示。
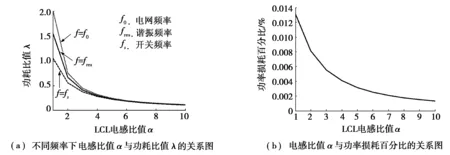
图4 电感比值 α与功率损耗的关系图
图4a是当频率分别为电网频率f0、谐振频率fres和开关频率fs时,电感比值α与功耗比值λ的关系图。由图4a可知:当频率为系统主要频率时,即电网频率、谐振频率和开关频率处,随着电感比值的增大,功耗比值减小。同时在3个主要谐波含量附近,随着α的增大,系统功率损耗比值逐渐减小,并且三者的差值越来越小。当α增大到5时,继续增大α值已经没有意义。图4b为分裂电容阻尼方案的功率损耗百分比与α的关系。由图4b可以看出:随着α的增大,功率损耗百分比越来越小。电感比值α由1增加至4时,功率损耗百分比变化明显;当α继续增大,功率损耗百分比减小缓慢。
α值越大,LCL滤波器中电感Ls对开关频率处的谐波抑制作用越大。但系统α不能无限增大,必须在谐振抑制能力和系统功率损耗之间折中,选择较为合适的α值。考虑LCL滤波器的谐振频率不能太小,否则会提高对电流控制器的设计要求以及系统设计复杂度。再者,在阻尼电阻一定的情况下,α的值对LCL滤波器的并网电流谐波抑制效果是不变的。综合考虑电流控制器的设计,α的取值为5较为合适。
为了验证参数选择的正确性,分析在阻尼电阻一定的情况下功耗比与其他参数的关系。图5为α=5时,功耗比值λ与频率的关系图。图5表明:在电感比值α=5时,系统功率损耗比值λ随着频率的不断增大而减小。在低频阶段,系统功率损耗变化比较小;而在高频阶段,由于频率大于谐振频率,功耗变化剧烈,在频率大于开关频率的一半时,变化率接近线性变化。
此外,还需进一步分析电阻的阻值对系统性能的影响。如果在实际的应用中,考虑刚才忽略的式(2)分母中s4项和分子中s3项系数的影响,分裂电容的阻尼电阻要略微大于Rf的α+1倍。取不同的Rd,绘制分裂电容阻尼方案传递函数波特图,如图6所示。
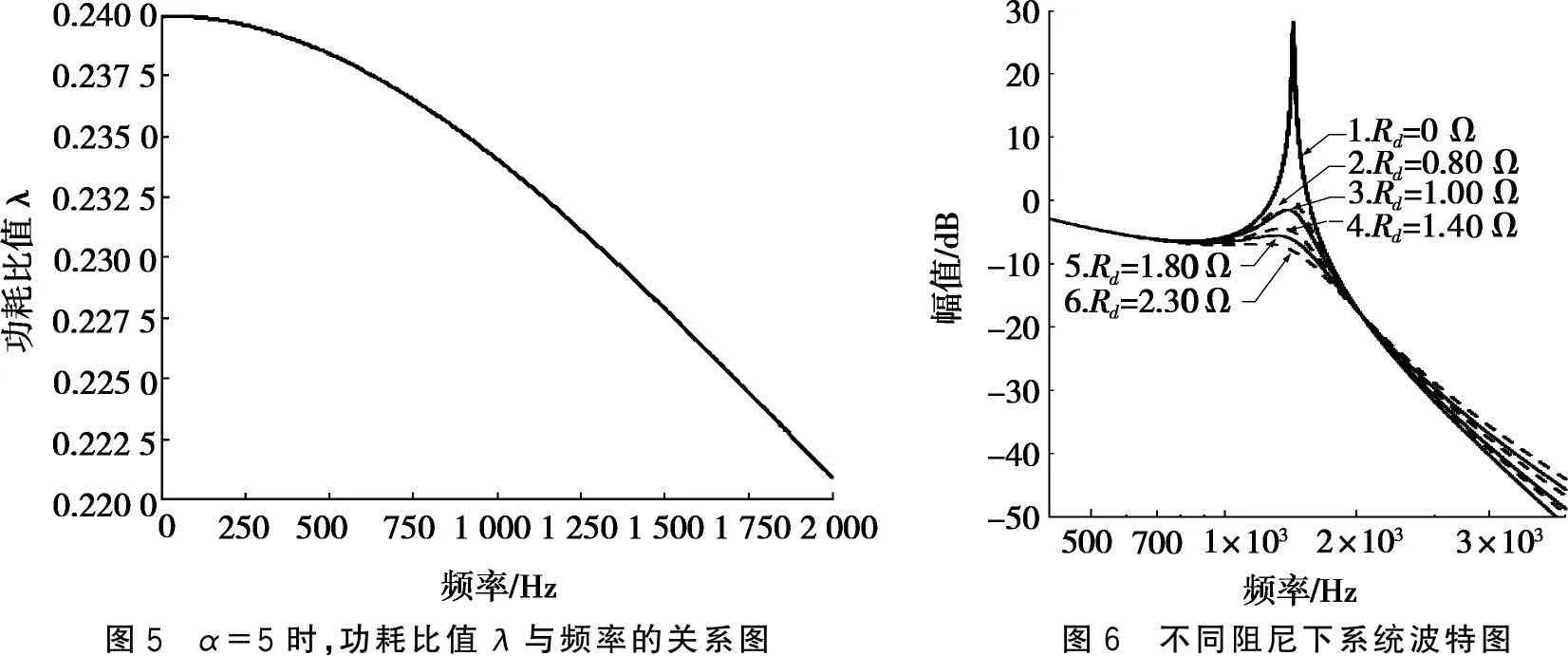
图5 α=5时,功耗比值λ与频率的关系图 图6 不同阻尼下系统波特图
图6中,曲线1~曲线6分别表示无阻尼电阻、串联0.80 Ω电阻、串联1.00 Ω电阻、串联1.40 Ω电阻、串联1.80 Ω电阻和串联2.30 Ω电阻时的系统波特图。由图6可知:通过串联电阻,谐振现象大幅度减弱。当电阻为Rd=6Rf=1.40 Ω时,仍有一个小峰波,但是其增益已经小于0 dB。随着电阻的增大,谐振峰得到有效地抑制,但是系统减弱了网侧电流高频谐波的衰减程度。综上所述,采用分裂电容无源阻尼法串联的电阻阻值为1.80 Ω,该电阻下系统的小波峰增益为-4 dB。
3系统控制策略
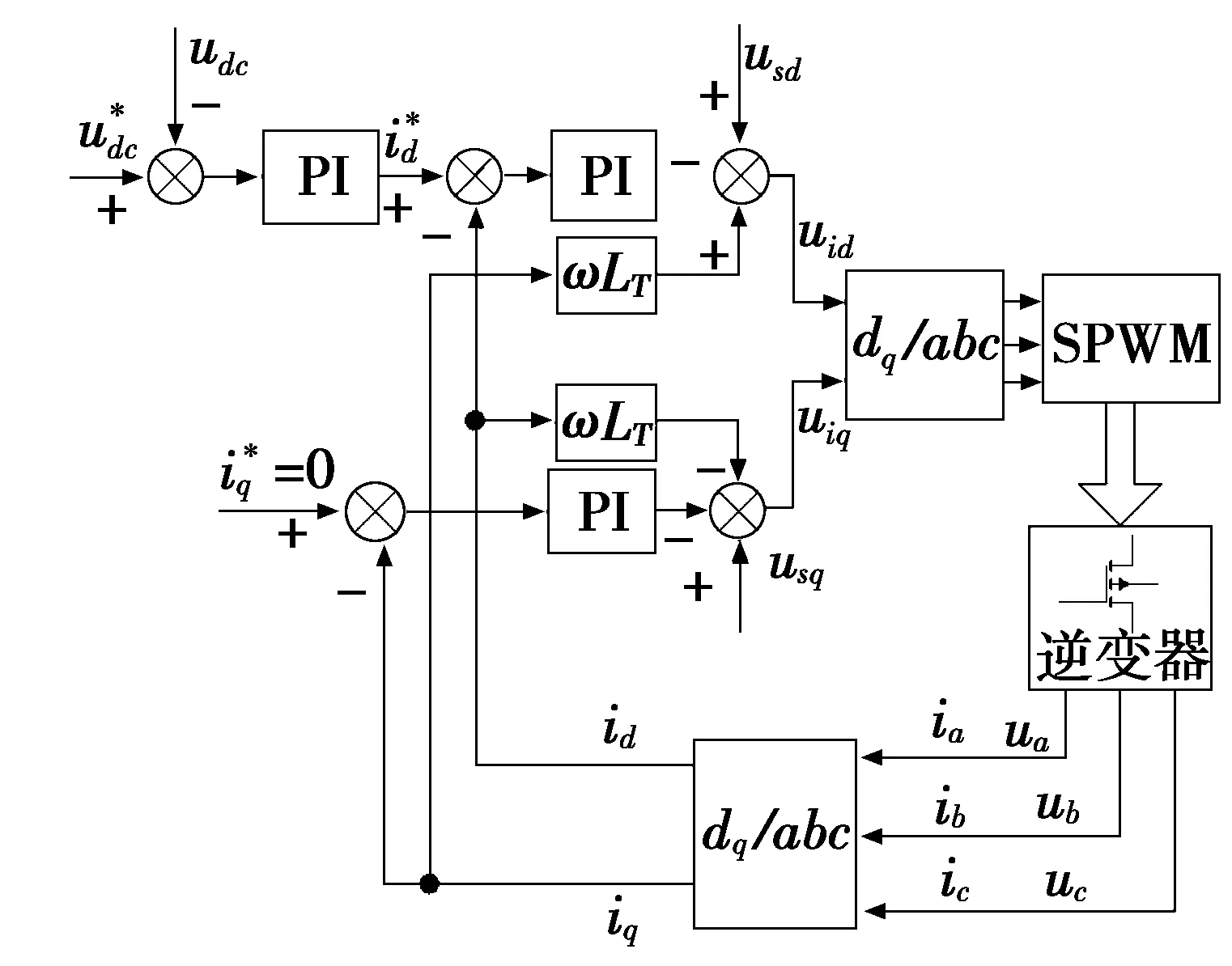
图7 三相逆变器的矢量控制框图
4仿真验证
为了进一步验证参数设计和控制策略的正确性和有效性,在MATLAB/Simulink仿真软件上搭建LCL型三相逆变器仿真平台,进行建模和仿真验证。系统参数上文已经给出。
图8是分裂电容阻尼方案的输出电压和输出电流仿真波形图。为了更好地对两种方案在滤波方面进行比较,对完全电容阻尼方案也进行了仿真。图9是采用完全电容阻尼方案的输出电压和输出电流仿真波形图。表1给出了在不同分裂电容容值比的情况下,并网电流总畸变率(THD)、谐振频率和开关频率处的谐波含量。
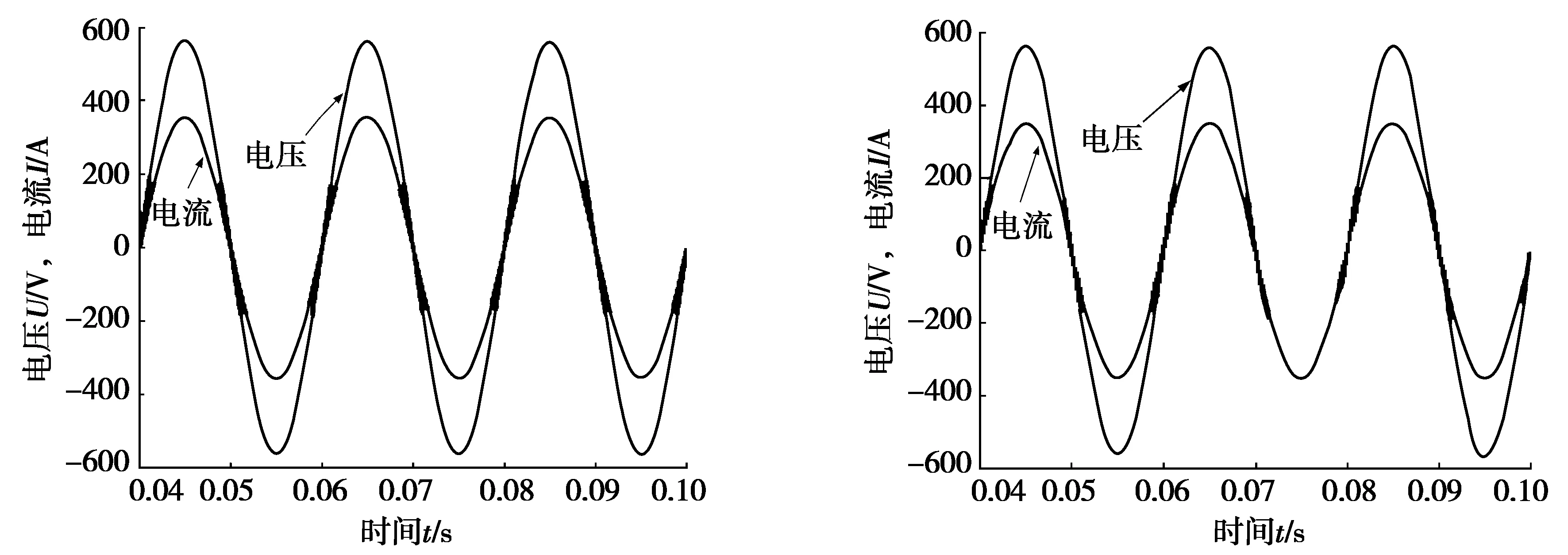
图8分裂电容阻尼方案的输出电压和输出电流图9完全电容阻尼方案的输出电压和输出电流
仿真波形图仿真波形图

表1 不同分裂电容容值比下的THD值及谐波含量
比较图8、图9和表1可知:本文所得出的分裂电容容值比α=5,较之完全电容阻尼方案,网侧电流中的高次谐波大大降低,电流的总谐波畸变率从2.23%下降到0.40%,电流的正弦性得到了很大的提高。分裂电容阻尼方案在滤除高次谐波方面有较大的优势,提高了并网电流质量。分裂电容容值比为5时,较之完全电容方案,THD值减少;而分裂电容容值比为1时,THD值稍微有所增加,由完全电容法的2.23%增加到2.64%,滤波性能同样有所减弱。因此,分裂电容容值比为5时,有更好的电流谐波衰减效果,且谐波含量在谐振频率和开关频率处也得到进一步地降低。
5结束语
本文针对传统LCL型逆变器存在的谐振现象,通过分析LCL滤波器的原理,采用无源阻尼法有效地消除了谐振现象,提出了全面的分裂电容无源阻尼方案的设计方法;并且从分析不同频率下的分裂电容与完全电容的功率损耗比出发,找出了功率损耗较小、控制器设计简单的电容容值比。系统采用电流内环和电压外环的控制策略,在MATLAB/Simulink仿真软件上,建立分裂电容LCL滤波器的并网型逆变仿真模型,所提出的电容容值比及其控制策略,可以有效地抑制LCL滤波器的谐振问题,减少系统功率损耗,在滤除电流谐波上有了很好的改进,电网电流总谐波畸变率大大减少,有效地提高了电网电流质量。
参考文献:
[1]LINDGREN M,SVENSSON J.Connecting fast switching voltage-source converters to the grid-harmonic distortion and its reduction[C]//IEEE Strock Power Tech Conference.Stockholm,1995.
[2]陈小宇,罗利文.并网型LCL滤波器中阻尼电阻的分析及设计[J].电气自动化,2012,34(2):26-27.
[3]郭小强,邬伟扬,顾和荣,等.并网逆变器LCL接口直接输出电流控制建模及稳定性分析[J].电工技术学报,2010,25(3):102-109.
[4]刘尚伟.单相LCL逆变器并网技术研究[D].武汉:华中科技大学,2011.
[5]DANNEHL J,LISERRE M,FUCHS F W.Filter-based active damping of voltage source converters with filter[J].IEEE transactions on industrial electronic,2011,58(8):3623-3633.
[6]沈国桥,徐德鸿.LCL 滤波并网逆变器的分裂电容法电流控制[J].中国电机工程学报,2008,28(18):36-41.
[7]王海松,王晗,张建文,等.LCL型并网逆变器的分裂电容无源阻尼控制[J].电网技术,2014,38(4):895-902.
[8]周志立,夏先文,徐立友.电动拖拉机驱动系统设计[J].河南科技大学学报(自然科学版),2015,36(5):78-80.
[9]刘超,赵争鸣,鲁挺.三电平PWM整流器网侧LCL滤波器设计[J].电工电能新技术,2012,31(1):56-59.
[10]郑昕昕,肖岚,王长宝.三相变流器LCL滤波器参数优化新方法[J].中国电机工程学报,2013,33(12):55-63.
[11]王盼,刘飞,查晓明.基于有源阻尼的并联有源滤波器输出LCL滤波器设计[J].电力自动化设备,2013,33(4):161-166.
[12]刘飞,查晓明,段善旭.三相并网逆变器 LCL滤波器的参数设计与研究[J].电工技术学报,2010,25(3):110-116.
[13]夏长亮.双馈风力发电系统设计与并网运行[M].北京:科学出版社,2014.
中图分类号:TM464
文献标志码:A
收稿日期:2015-11-21
作者简介:刘莹(1991-),女,江西吉安人,硕士生;于仲安(1973-),男,甘肃临洮人,副教授,硕士,硕士生导师,研究方向为计算机控制技术.
基金项目:国家自然科学基金项目(51177066)
文章编号:1672-6871(2016)03-0053-05
DOI:10.15926/j.cnki.issn1672-6871.2016.03.012
