基于全时域势流理论的船舶与液舱晃荡耦合运动的数值计算

李裕龙，朱仁传，缪国平，范 菊

（上海交通大学 船舶海洋与建筑工程学院，海洋工程国家重点试验室，上海 200240）

基于全时域势流理论的船舶与液舱晃荡耦合运动的数值计算

李裕龙，朱仁传，缪国平，范 菊

（上海交通大学 船舶海洋与建筑工程学院，海洋工程国家重点试验室，上海 200240）

基于三维线性有航速时域势流理论计算船体时域运动外域波浪力，同时采用三维全非线性时域势流理论来计算舱内液体的非线性晃荡所诱导力与力矩，进而建立了波浪中载液船舶耦合运动方程。该方法能够完整地考虑波浪、船体和液舱晃荡之间的实时耦合作用。研究结果表明：通过模型实验和数值模拟计算的对比，数值模拟计算能够清晰显现出液舱晃荡对船体全局运动影响，无航速船体运动RAO与模型实验结果吻合良好，有航速运动计算合乎预期。

液舱晃荡；耦合运动；非线性时域；有航速理论

0 引 言

船舶在波浪上的运动激励液舱内的液体产生晃荡，液舱晃荡诱导的冲击力同时作用在舱壁上，进而影响到船舶的运动姿态。船舶运动与液舱晃荡之间的耦合效应研究一直是船舶与海洋工程界一直关注的问题，合适且高效的理论与数值计算方法对探讨分析船舶运动与液舱晃荡之间的耦合效应是十分重要的。目前国内外许多学者已对船舶运动与液舱晃荡之间耦合效应进行了一些分析与研究工作[1-3]，综合来说，基于势流理论的耦合效应的相关研究主要可分为两种途径：相关领域的模型试验研究[4]，以及用来辅助实验研究且专门针对本问题的数值计算工作[5-6]。

船舶在波浪上的运动计算是船舶与海洋工程领域的经典问题。如果考虑到晃荡流体的非线性作用，则需要在时域下来分析船舶运动。时域三维Rankine源边界元方法相对于复杂时域格林函数方法，虽然其需要加以粘性处理辐射面，或者是借助于匹配面的方法处理舰船时域远场波浪，但其编程相对简单以及其对船型几何外形适应性更强的优点仍然在学术界引起足够重视。本文使用时域三维Rankine源边界元方法以及脉冲响应理论模拟时域舰船有航速运动。

液舱流体晃荡问题在学术界与工程界中同样是经典的水动力学问题。自从液化天然气船等载液高附加值船舶的迅速发展，液舱流体晃荡业已成为水动力学研究工作的热点问题。已有很多学者分别采用了频域势流理论、时域非线性势流理论、粘性流理论方法来研究模拟液舱晃荡问题及其诱导的水动力砰击载荷。本文采用时域非线性势流理论，藉此配合舰船时域线性有航速势流理论，构建了完全时域下的舰船耦合液舱晃荡时域运动计算方法，为基于势流理论研究舰船耦合液舱晃荡现象提供了新的途径。

本文将船舶在波浪上的运动问题和液舱内液体晃荡问题采用不同的时域势流理论求解，船舶的运动采用基于脉冲响应函数理论的三维线性有航速时域势流理论，计算首先需要求得有航速水动力系数以及脉冲响应函数，以及时域下的绕射问题，进而求解时域有航速舰船时域运动方程。本文同时应用三维非线性时域势流理论模拟非线性液舱晃荡问题，将实时诱导力与力矩在同一时刻添加入船舶有航速时域运动方程，从而建立了载液船舶在波浪上运动的有航速时域运动方程。这种方法在零航速时刻能够模拟常见的无航速计算工况与载液浮式结构物的运动响应，同时能够进行有航速的载液舰船时域运动模拟，具有很好的适用范围。通过对加载方形液舱的S175船模进行耦合运动的数值模拟及与实验结果的对比，以及有航速舰船的数值计算结果，验证了本文数值计算方法的准确性，表明使用本文提出的方法进行载液有航速舰船时域运动是完全可行的。基于此本文通过对一艘载液15000GT船横摇运动进行了计算分析，更进一步的拓展了计算代码的实用性与可靠性。

1 载液船舶耦合运动相关基本理论

图1 船体运动的纵坐标系示意图Fig.1 The coordinate system of ship motion

1.1 载液船舶在波浪上的运动

本文采用势流理论求解船舶在波浪上的运动。这里给出加载液舱的船舶在波浪上运动满足的数学模型。线性入射波速度势有以下形式：

式中：ζI，ω，k分别为入射波的波幅，自然频率与波数，ωe为遭遇频率。定义随船体运动的笛卡尔坐标系坐标系示意图见图1。在规则波激励下船舶保持固定的航速作六自由度运动。

本文采用三维有航速时域势流理论求解外域流场的速度势函数。船舶运动辐射问题速度势所满足的流场边界条件如下：

根据时域分析的脉冲响应方法，能够将辐射势进一步为瞬时项和记忆项。在线性系统下，时域辐射系统的输入为浮体的k模态的运动速度。假定浮体的初始位移则辐射问题的物面条件能够有如下的表达式[7]：

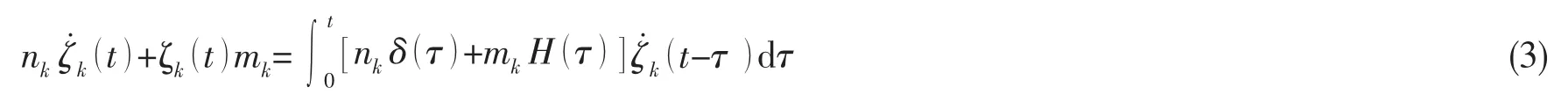
辐射势的脉冲响应函数根据物面条件分解如下：

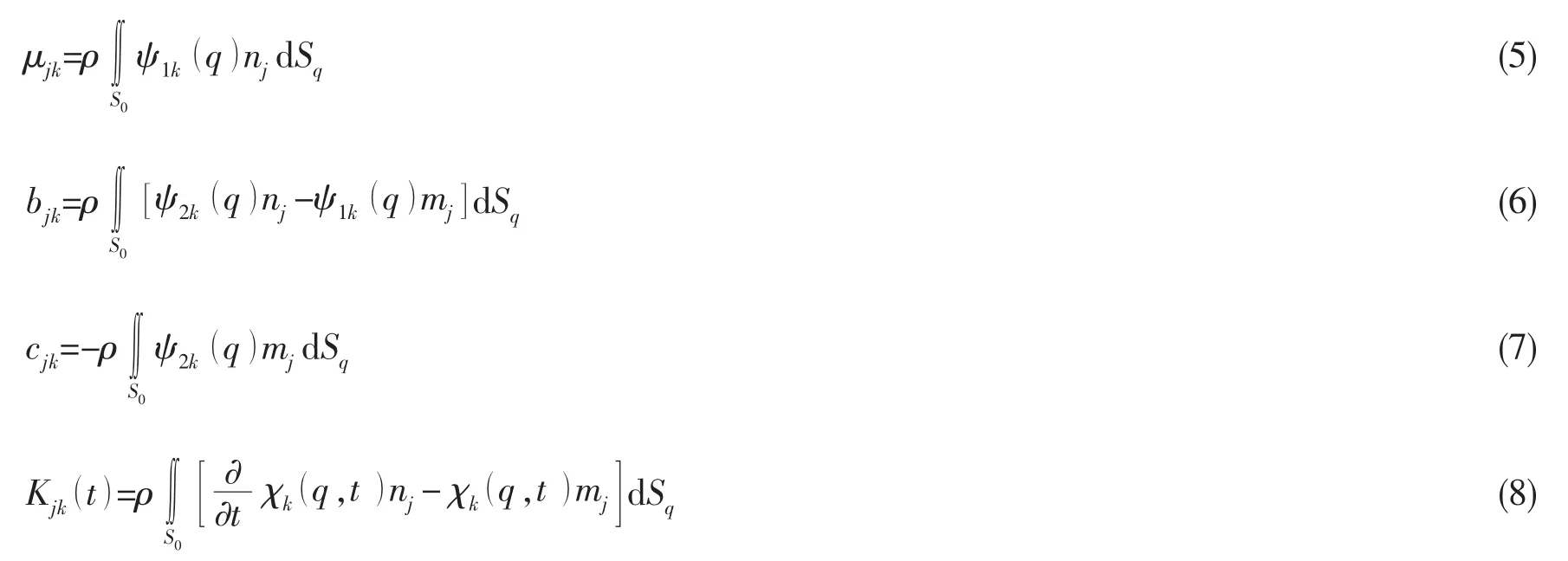
进而便可获得舰船辐射运动的辐射力：

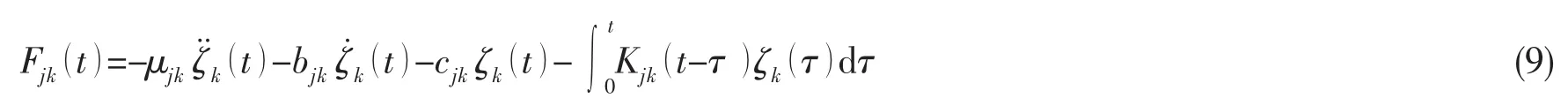
其中：附加质量μjk取决于船体的外表面几何形状，bjk和cjk取决于船的几何形状和船速。较为复杂的记忆效应体现在时延函数中，其取决于船体外表面的的几何外形与航行速度。

同样，将波浪的运动视为简谐运动，且将入射波波高ζI作为绕射系统的输入，同样使用脉冲响应理论求解绕射问题，便可求得舰船运动的外部波浪力。

1.2 基于三维全非线性势流理论的液舱晃荡问题

本文选取动坐标系作为计算坐标系，其优势在于壁面相对于动坐标系保持静止，这样便给势流计算带来不少便利。液舱动坐标系如图2所示。

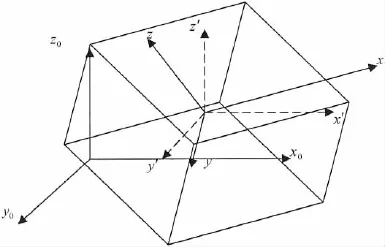
图2 所选液舱坐标系示意图Fig.2 The coordinate system of the tank

速度势函数满足的控制即拉普拉斯方程如下：

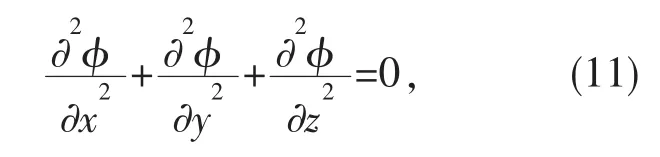
在流域内

自由表面上动力学边界条件：

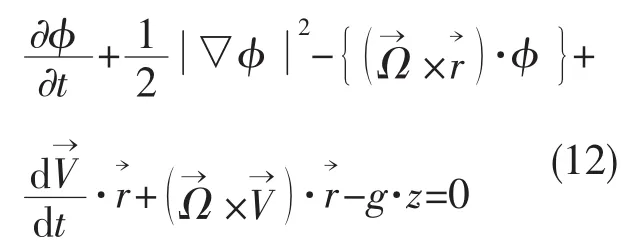
自由表面上运动学边界条件：

舱壁上的边界条件：

为了要计算实时自由面的变化，自然必须计及自由液面处的速度势和波高随时间的变化。不同时刻的自由面升高与速度势，需要采用时间的差分方式来计算。得到边界上每点的速度势后，根据非线性拉格朗日方程：

便能够方便计算出边界处该时刻的压力。通过将压力沿着液舱所有壁面的积分就能够计算当前时刻液舱晃荡对壁面诱导的晃荡力与力矩。在计算中同时需要实时对自由液面进行光顺化处理。

2 载液船舶在波浪上时域运动的数值算法

在液舱晃荡问题的非定常计算求解过程中，在某一计算时刻通过对液舱壁面的压力积分可以得到当前时刻下液舱晃荡在舱壁上诱导的水动力幅值。晃荡诱导的水动力进而会影响到船舶的运动姿态，因此载液船舶时域运动方程需要在当前时间步下建立。耦合液舱晃荡作用下的时域船舶全局运动方程有如下形式：

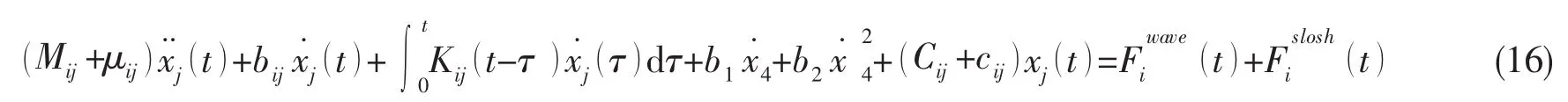
图3 S175船型线Fig.3 Main parameters of LNG ship

3 数值计算

3.1 S175船模主尺度与有航速时域计算

数值计算工作采用的是高速集装箱船型S175，其船型线见图3所示。其无航速船舶耦合液舱晃荡的模型试验是在中国船舶科学研究中心耐波性水池中进行[8]，试验模型是一条加载了一个方形液舱的S175船模，模型与实船的缩尺比为1:55，其具体的主尺度参数见表1。

表1 LNG主尺度Tab.1 Principal dimensions of LNG

所加载的液舱为方形液舱，其尺寸和安装位置见图4。液舱长度为600 mm，宽度为300 mm，高度为250 mm，舱内液体的深度为125 mm，液舱重心位置与船模重心位置重合。

图5和图6给出了S175船的时域运动响应幅值的数值计算结果与实验结果的对比。数值结果与实验结果两者吻合良好。无论是水动力系数还是幅值响应，计算程序都能够给出较为令人满意的计算结果。这验证了有航速时域计算的有效性。

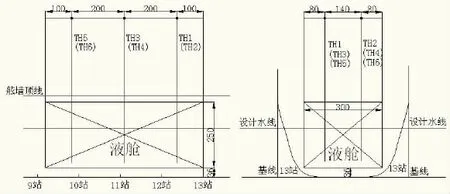
图4 加载液舱的尺寸与位置Fig.4 Size and location of tank

图5 迎浪工况下数值与实验所得的S175船模垂荡RAOFig.5 Comparison of heave RAO of ship in head sea by experiment and calculation

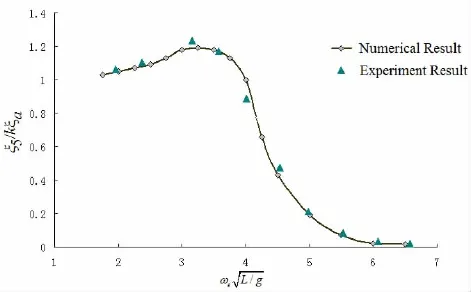
图6 迎浪工况下数值与实验所得的S175船模纵摇RAOFig.6 Comparison of Pitch RAO of ship in head sea by experiment and calculation

3.2 无航速耦合液舱晃荡船舶时域运动的数值计算

本节给出S175船舶在无航速情况下的计算结果与模型实验结果作为耦合计算的验证。这里将有航速耦合计算程序中的航速设为零。为了验证程序的有效性，这里给出了S175船的无航速的RAO曲线与实验结果的对比。可以预计，在无航速下的结果如果能够符合实验结果，便可以首先验证时域运动方程与液舱晃荡问题计算无误。这里就加载了方形液舱的S175船模，在迎浪和横浪两个工况下进行了无航速耦合运动的时域数值计算。

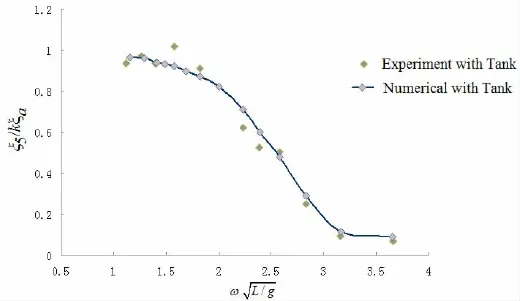
图7 迎浪工况下数值与实验所得的S175船模纵摇RAOFig.7 Comparison of pitch RAO of ship in head sea by experiment and calculation

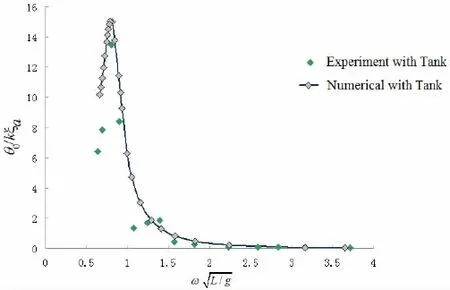
图8 横浪工况下数值与实验所得的S175船模横摇RAOFig.8 Comparison of roll RAO of ship in head sea by experiment and calculation

从图中可以看出数值计算与模型实验的结果同样吻合较好，在此阶段验证了耦合计算程序中液舱晃荡模块与耦合计算模块的有效性，并且经由有航速船舶的计算结果的准确性，便能够预测出本文提出的有航速船舶耦合液舱晃荡时域计算方法的可靠与有效性。

3.3 有航速耦合液舱晃荡船舶时域运动的数值计算

在上一节无航速计算结果准确的基础上，以及有航速时域数值计算能够保证计算精度的前提下，便可以方便地进行有航速船舶耦合液舱晃荡的时域数值计算工作。图9至图12给出了不同航速下船舶耦合液舱晃荡时域运动的纵摇以及横摇模态的响应曲线。

图9 迎浪工况下加载与不加载液舱所得的S175船模纵摇RAO（Fn=0.10）Fig.9 Comparison of pitch RAO of ship in head sea of with tank and without tank(Fn=0.10)

图10 横浪工况下加载与不加载液舱所得的S175船模横摇RAO（Fn=0.10）Fig.10 Comparison of roll RAO of ship in head sea of with tank and without tank(Fn=0.10)

在图9至图12中给出了加载液舱有航速S175船横摇与纵摇的运动响应曲线，其中为了对比同时给出了不加载液舱的S175船的时域运动曲线。在RAO中的横坐标的ω为波浪自然频率。从计算结果可以看出，液舱晃荡对于不同航速下船舶的纵向运动影响不是很大，并且在计算中观察到垂荡运动所受液舱晃荡的影响也并不明显，但是随着船舶的纵向舱室加多或者几何形状的改变对纵摇的影响需要在实际计算中加以确定。而在船舶的有航速横浪运动时，其运动规律与无航速时趋势大致相同。加载液舱船舶在低于船舶自身的横摇自振频率下运动响应高于不加载液舱的运动幅值，其峰值也大于无载液船舶横摇运动峰值，其原因是此时液舱所诱导的力矩与船舶的波浪诱导力矩幅值叠加所造成的。并且从上一节可以看到，本文的无航速计算结果同实验结果对比良好，即这种数值方法可以直接对无航速载液船舶的时域运动响应进行预报。

图11 迎浪工况下加载与不加载液舱所得的S175船模纵摇RAO（Fn=0.30）Fig.11 Comparison of pitch RAO of ship in head sea of with tank and without tank(Fn=0.30)

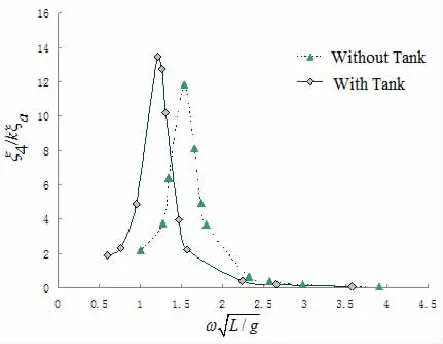
图12 横浪工况下加载与不加载液舱所得的S175船模横摇RAO（Fn=0.30）Fig.12 Comparison of roll RAO of ship in head sea of with tank and without tank(Fn=0.30)

3.4 载液15000GT集装箱船横摇运动时域数值计算

为了拓展计算代码的实用性，本文选取了一艘具有实验数据的集装箱船15000GT作为计算算例[9]，针对不同加载深度的液舱与15000GT船模的耦合横摇运动做了数值计算研究。图13是15000GT的边界元计算网格。

模型试验中对船舶在无航速规则波作用下的横向运动响应做了测量与分析。液舱尺寸与几何位置见表2和图14。模型试验重点在于测量不同深度装载的液舱对横摇运动的影响，并且对于不加载液舱的船模在同样来波工况中的运动响应做了测量。加载不同深度的液舱的模型工况见表3。

图13 15000GT船边界元计算网格Fig.13 The boundary mesh of 15000GT container ship

图14 液舱位置简图Fig.14 Schematic profile of the rectangle tank

表2 液舱的几何尺寸与位置Tabl.2 Main dimension of rectangle tank

表3 模型试验工况Tab.3 Experiment parameters

图15 水深8 cm液舱15000GT集装箱船横摇RAOFig.15 Roll RAO of 15000GT container ship model with 8 cm depth liquid tank

图15-17为在液舱不同装载深度下的船模横摇运动RAO曲线与实验值的对比结果，如图所示数值计算结果趋势与实验结果吻合良好，验证了本文所提出的数值计算方法对于不同工况横摇运动计算的可行性，拓展并延伸了计算代码的实用性。

从图15-17可以看出，不同装载下的液舱对横摇运动有着很大的影响，且程度随装载的深度的增加而增大。首先是幅值，随着装载深度的增加，其幅值逐渐减小，其原因是液舱诱导的内部力随着装载深度的增加而增大，且由于液舱几何外形所致，在当前激励频率下其相位与波浪所激励的外部力的相位一直有着180度左右的偏差，其合成作用便是减小船舶受到的外部力，因此船舶的横摇幅值逐渐减小。并且随着装载深度的增加，液舱内部的液体的固有频率也会逐渐变化，并且与当前运动模态的自由液面尺度相关，并且晃荡随着激励频率接近共振频率时，其液面高度随时间的变化会颇为剧烈，当前装载下所诱导的最大波面升高所包含的非线性因素也会影响船舶的横摇共振频率。并且由于液舱内部液体的形状随着运动的幅值会逐渐变化，从简单的角度来说液舱内部液体的重心由于液体形状变化同样产生偏移，这样便致使船舶的稳心同样会发生变化，因此横摇运动自然会受到不同程度的影响。

图16 水深10 cm液舱15000GT集装箱船横摇RAOFig.16 Roll RAO of 15000GT container ship model with 10 cm depth liquid tank

图17 水深12 cm液舱15000GT集装箱船横摇RAOFig.17 Roll RAO of 15000GT container ship model with 12 cm depth liquid tank

4 结 论

本文在成功地将船舶在波浪上运动和液舱内液体晃荡问题分析同时采用时域势流理论求解。时域船舶运动问题采用基于势流理论的脉冲响应函数及Rankine源边界元法求解，非定常液舱晃荡问题采用非线性时域势流理论和Rankine源边界元方法求解。本文基于目前的研究结果，能够得出以下结论：

液舱晃荡效应对载液船舶在波浪上的运动有着较为重要的影响，特别是对于横浪工况下的横摇运动。船舶运动的遭遇频率在船舶响应频率范围附近时，液舱晃荡诱导的横摇力矩同波浪诱导的横摇力矩之间的相位差在一定程度上减小了船舶横摇运动的幅值。在较低频率的入射波激励下，液舱晃荡诱导的横摇力矩同波浪诱导的横摇力矩之间的相位差较小，两种横摇力矩的叠加会增大船舶的横摇运动幅值。在横浪工况下，液舱晃荡对船舶的垂荡运动影响较小。在迎浪工况下，随着航速提高，本文所取算例来看液舱晃荡所诱导的外力与外力矩对船舶的垂荡与纵摇等纵向运动的幅值影响均比较小。

本文采用的数值计算方法适用于计算分析载液船舶在波浪上的时域运动，不仅适用于船舶的无航速时域运动，同样还可以适用和拓展到有航速的船舶时域运动。本研究所用的计算液舱的几何形状规则，而其他各异的几何形状的液舱，与不同类型的液舱布置，均会对载液船舶运动造成不同的影响，其运动规律取决于船舶的几何外形与航行工况。因此本文所得出的结论证明了开发的计算程序的准确性，但是对于不同类型的载液船舶由于其几何因素与设计理念差异颇大，本文的计算结论对其他各异的载液船型应该不具有完全的推广性，针对不同的船舶需要更进一步的详细计算。

本文方法由于基于脉冲响应函数方法，具有较高的计算效率，数值计算与试验结果吻合良好，为设计载液船舶或减摇水舱等的前期设计提供了快速有效的分析方法和技术手段。这种方法的局限性在于无法处理自由液面破碎等强非线性现象，但可以较好地预报船体与液舱晃荡耦合运动的共振频率区间与基本幅值。

[1]Kim Kyung sung,Kim Moo Hyun.Sloshing effects on Multi-Vessel motions by using moving particle simulation[C]//Proceedings of the 21th International Offshore and Polar Engineering Conference,June 19-24,2011.Maui,Hawaii,USA, 2011:39-45.

[2]Huang Z J,Danaczko M A,Esenkov O E,Martin C B,et al.Coupled tank sloshing and LNG carrier motions[C]//Proceedings of the 19th International Offshore and Polar Engineering Conference,June 21-26,2009.Osaka,Japan,2009: 92-99.

[3]Wang X,Arai Makoto.A study on coupling effect between sea-keeping and sloshing for membrane-type LNG carrier[C]// Proceedings of the 20th International Offshore and Polar Engineering Conference,June 20-25,2010.Beijing,China, 2010:245-251.

[4]Nam Bo-Woo,Kim Yonghwan,Kim Dae-Woong,Kim Yong-soo.Experimental and numerical studies on ship motion responses coupled with sloshing in waves[J].Journal of Ship Research,2009,53(2):68-82.

[5]Tabri Kristjan,Matusiak Jerzy,Varsta Petri.Sloshing interaction in ship collisions-An experimental and numerical study [J].Ocean Engineering,2009,36:1366-1376.

[6]Kaminski Miroslaw Lech,Bogaert Hannes.Full scale sloshing impact tests[C]//Proceedings of the 19th International Offshore and Polar Engineering Conference,June 21-26,2009.Osaka,Japan,2009:125-134.

[7]戴遗山,段文洋.船舶在波浪中运动的时域理论[M].北京:国防工业出版社,2008.

[8]邹 康.耦合液舱晃荡的船舶运动性能研究[D].镇江:江苏科技大学,2009.

[9]洪 亮,朱仁传,缪国平,范 菊.波浪中船体与液舱晃荡耦合运动的时域数值计算[J].哈尔滨工程大学学报,2012, 33(5):635-641.

Numerical method of ship motions coupled with tank sloshing based on fully time domain potential flow theory

LI Yu-long,ZHU Ren-chuan,MIAO Guo-ping,FAN Ju
(The State Key Laboratory of Ocean Engineering,School of Naval Architecture,Ocean and Civil Engineering, Shanghai Jiao Tong University,Shanghai 200240,China)

Based on three dimensional time domain potential theory,ship motion is solved by using an impulse response function method and boundary element method.Using three dimensional fully nonlinear time domain potential theory to simulate the nonlinear tank sloshing.Then the ship motion coupled with tank sloshing is established that the interactions of wave,ship body and tank sloshing are completely taken into considerations.Numerical simulation and experimental studies indicate that the numerical results of ship motion coupled with tank sloshing can clearly show the coupling effect of tank sloshing on the ship global motion.The results of the ship motion RAO of both computational and experiment ones are in good agreement, the numerical result of ship which has forward speed with liquid tank is also agreed with expectation.

tank sloshing;coupling motion;nonlinear time domain;ship speed

O35

A

10.3969/j.issn.1007-7294.2016.07.003

1007-7294（2016）11-1369-12

2016-01-09

工业和信息化部高技术船舶科研项目资助（2007K24161）

李裕龙（1985-），男，博士研究生；朱仁传（1969-），男，教授，博士生导师，通讯作者，E-mail：renchuan@sjtu.edu.cn。