基于三角形斯坦纳树的分区连通性恢复算法*

秦宁宁，吴德恩，余颖华（.江南大学物联网工程学院，江苏无锡2422；2.江南大学轻工过程先进控制教育部重点实验室，江苏无锡2422）



基于三角形斯坦纳树的分区连通性恢复算法*

秦宁宁1，2*，吴德恩1，余颖华1
（1.江南大学物联网工程学院，江苏无锡214122；2.江南大学轻工过程先进控制教育部重点实验室，江苏无锡214122）

摘要：无线传感器网络中的节点由于自身能量的消耗，及外部因素影响会导致节点出现大规模的失效，从而把无线传感器网络分割成几个独立的不能相互通信的分区。为恢复网络，重建分区之间的通信链路，提出基于三角形斯坦纳树连通恢复算法。该算法首先利用传统算法实现分区连通，然后通过构建三角形斯坦纳树以减少部署的中继节点数量。与现有的一些算法相比，该方法形成的网络拓扑不仅减少了部署中继节点的数量，能够使分区重新连通，而且能够减少网络通信的能量消耗。实验结果表明，所提方法相对于传统算法在构建网络拓扑时更加有效。

关键词：无线传感器网络；连通性；三角形斯坦纳树；分区

项目来源：江苏省“六大人才高峰”第十一批高层次人才项目（DZXX-026）；2014年国家公派高级研究学者及访问学者（含博士后）项目；国家自然科学基金项目（61304264）；江苏高校优势学科建设工程项目；江苏省产学研联合创新资金前瞻性联合研究项目（BY2014023-31）；中央高校基本科研业务费专项资金项目（JUSRP51510）

无线传感器网络中的节点具有体积小、成本低等特点［1-3］，在提高网络应用灵活性的同时，也决定了节点不可能携带可供长期使用的能量模块。在恶劣的环境下，能量有限的节点很容易受自然环境或人为因素的影响而出现大规模的损坏［4-6］，造成网络分割成独立分区而不能相互通信，从而丧失了监测能力。因此，恢复网络的连通性成为一个至关重要的研究课题［7］。

在恢复受损网络的连通性工作中，部署中继节点无疑是一个快速有效的方法［8］。通常中继节点拥有比普通节点更多的能量，更远的通信范围［9］，以其作为各个分离分区之间的重建桥梁，可以解决分区之间的连通性问题［10］。在中继修复过程中，最关键的问题是如何能部署更少的中继节点同时确保相互独立的分区能重新进行通信［11］。

为了以更少的中继节点恢复分区的连通性，许多启发式方法已经被提出。文献［7］提出通过重置失效节点的邻居位置来恢复网络连通，然而这种方法不能处理多节点同时失效情况，且不能处理部分区域内节点不能移动的情况。文献［12］中的MST_ 1TRNP（Minimum Spanning Trees Algorithm Based on a Single-Tiered Relay Node Placement）算法采用krus⁃kal或prim算法寻找最小生成树，根据边长与中继节点通信半径，沿着树的边部署中继节点恢复连通，但该方法复杂度较高，且恢复后网络的节点平均连通度较低。为了提高节点平均连通度，单连通蜘蛛网1C-SpiderWeb（1-Connected Spiderweb）算法［13］通过形成一个类似于蜘蛛网的网络结构完成中继节点布置，虽然提高了节点平均连通度，但大量中继节点的布置代价降低了网络效率，增大了分区间数据传输延迟。基于网格优化的分布式中继节点布置算法［14］CORP（Cell-based Optimized Relay node Placement al⁃gorithm）将网络划分为大小相等的网格单元，根据分区所在网格位置，由外向内画长方形找到最短路径，布置额外节点重建各个分区连接。所形成的网络拓扑能均衡网络数据传输量，降低了分区间数据传输延迟，但复杂度较高，不适合在大规模网络中使用。

为克服调度中继节点补位过程中，在复杂度、效率、数据传输延迟等多方面性能难于兼顾的问题。论文提出了基于三角形斯坦纳树连通性恢复算法CRATST（Connectivity Recovery Algorithm based on Triangle Steiner Tree），通过引入斯坦纳点，构造三角形斯坦纳树，减少恢复分区连通性所需的中继节点数量，降低分区间通信的距离与能量消耗，提高网络的性能。

1　网络描述

1.1网络模型

在给定空间A内部署的传感器网络S={Si| i=1,2,̌,N}遭受到大规模的破坏后，可能会被分裂成若干无法直接通信的子区域。如图1所示，灰色圆点表示失效节点，白色圆点表示正常工作节点，若将能正常工作节点形成的孤立网络称为分区，则图1中存在7个分区，并以Segi代表第i个分区，i=1,2,̌,Nseg，其中Nseg为分区数量。显然，分区内的节点能够相互进行通信，分区间不能通信。

不失一般性，设定网络为静态同构网络，即所有节点具有相同的感知半径r和通信半径R。部署的中继节点与已有节点具有相同的感知半径和通信半径。节点可以利用已有的定位算法获得自身位置信息［15］。

图1　网络受破坏后，形成独立分区

1.2相关知识与定义

定义1三角形的斯坦纳点：三角形内到三顶点距离之和最小的点即为三角形的斯坦纳点［16］。

对于给定网络S，任意三个相邻的节点Si,Sj,Sk构成三角形△SiSjSk，且其中不包含其它节点。若△SiSjSk中存在斯坦纳点Q，根据文献［16］关于三角形斯坦纳点的位置特征，结合△SiSjSk的内角大小，Q的位置可基于如下2种情况进行确定。

①∠SiSjSk,SjSiSk,SiSkSj<

若∠SiSjSk,SjSiSk,SiSkSj<，根据文献［16］可知，点Q必在三角形内，且与△SiSjSk任意两点连线的夹角均为，如图2（a）所示，即式（1）成立。

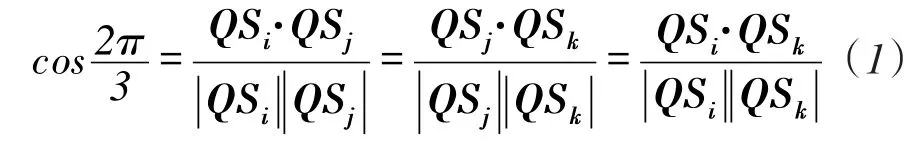
则基于式（1），可确定斯坦纳点Q的坐标。

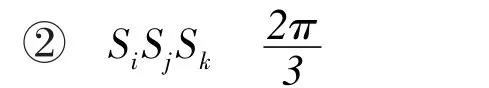
若△SiSjSk中存在某内角∠SiSjSk≥，根据文献［16］可知，其斯坦纳点Q与三角形钝角顶点重合，如图2（b）所示。

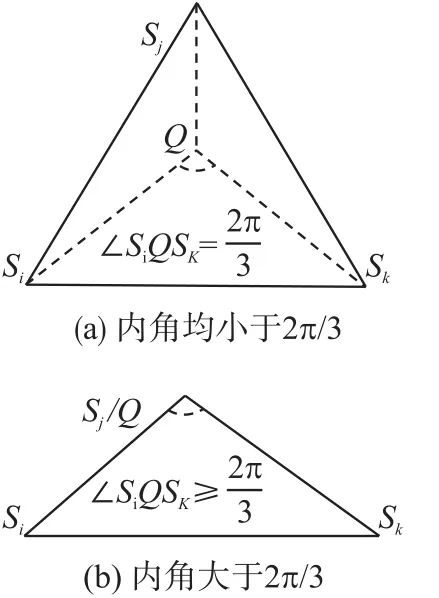
图2　斯坦纳点Q位置

定义2三角形斯坦纳树：对于平面中能够组成三角形的三个点，分别连接该三角形斯坦纳点与三个点，从而使三个点连通，连通后的结构称为三角形斯坦纳树。

2　 CRATST算法

寻找最小斯坦纳树已被证明是一个NP难问题［17］，论文提出启发式算法CRATST解决该问题。CRATST算法旨在用较少的中继节点恢复分区连通性，同时获得较好的网络拓扑。该算法首先通过传统方法恢复分区连通性，然后通过构建斯坦纳树减少中继节点数量。具体分为初始部署，启发式部署，斯坦纳部署，检查部署四个阶段，逐步减少中继节点数量实现分区的连通。

2.1初始部署

初始部署启动后，根据给定的目标区域A计算A的几何中心为O点。在每个分区Segi与网络区域中心O的连线上，每隔距离R部署一个中继节点，实现每个分区与区域中心O的连通。为了确保所有分区间能够相互连通，在O位置部署中继节点。

以Dist(Segi,O)表示分区Segi与中心O的距离，则每条路径部署中继节点的数量为：

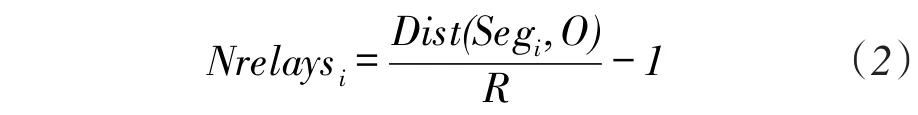
2.2启发式部署

为了减少初步部署的中继节点数量，需对初始部署后的网络进行优化。通过确定各个分区在顺时针方向的排序，生成启发式部署。排序步骤如下：

Step 1将区域中心O当作平面直角坐标系原点，比较每个分区与区域中心O横纵坐标的大小，将所有分区划分为以O为原点的4个象限。

Step 2求出所有分区与区域中心O连线的斜率，将各个象限内的分区根据斜率按从大到小顺序排列。

Step 3将每个象限的分区排序按一四三二象限的顺序串联起来，即可得到分区相对于中心O在顺时针方向的排序集合Turn。论文将排序中某个分区的前后两个分区称为该分区的相邻分区。

分区确定排序后，启动启发式部署。启发式部署伪代码如表1所示。

表1　启发式部署伪代码

若Nij用来表示相邻分区对Segi,Segj与中心位置O部署的中继节点总数，则

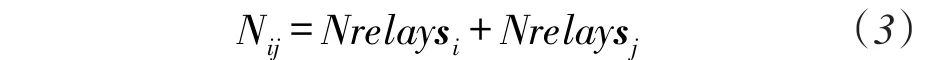
2.3斯坦纳部署

通过构造三角形斯坦纳树恢复相邻分区对Segi,Segj与中心O三点的连通性，并与启发式部署进行对比，进一步精减部署中继节点的数量。若启发式部署所需中继数更少，则保留启发式部署方案；如更多，则启动斯坦纳部署方案。斯坦纳部署伪代码如表2所示。

通过斯坦纳部署，进一步优化了部署的中继节点数量，但同时改变了启发式形成的拓扑，可能造成一些分区不能与其他分区连通，故需要检查部署以实现所有分区连通。

表2　斯坦纳部署伪代码

2.4检查部署

根据斯坦纳部署阶段可知，未被选中且在启发式部署阶段提前终止部署的分区Segk可能会由于相邻分区Segl的网络拓扑已经改变，导致Seggk不能与其他分区连通，因此需在分区Segk与O之间补充部署中继节点，从而实现所有分区之间的连通。

2.5算法复杂度分析

1C-SpiderWeb算法在恢复分区连通性的过程中，只进行了一次优化，而CRATST算法除了采用同样的优化方法之外，进行了二次优化，以尽可能减少部署的中继节点数量。故CRATST算法性能的改善建立在复杂度提高的基础上。

3　算法案例

以图1中网络为案例，阐述CRATST恢复分区的连通性的具体操作步骤。抽象后的拓扑图如图3 （a）中所示，依原7个分区位置对应抽象为Segi(i=1,2,…,7)共计7个分区节点，彼此不连通。

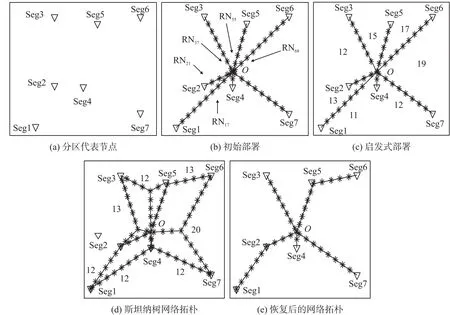
图3　CRATST算法案例

首先，每个分区Segi沿着中心O的方向部署中继节点，如图3（b）。

基于分区与O的距离确定集合D={Seg1,Seg6, Seg7,Seg3,Seg5,Seg2,Seg4}。经计算得到RN17和RN21、RN68和RN55、RN37和RN55分别能够进行通信，因此分区Seg1、Seg6、Seg3的中继节点将分别部署到RN17、RN68、RN37就停止，而分区Seg2,Seg4,Seg5,Seg7则保持初始部署阶段形成的拓扑与O连通，如图3（c）。

然后，基于3（a）重构斯坦纳树完成相邻分区对与O的连通，如图3（d），确定每个三角形斯坦纳树部署的中继节点数量。基于Tij确定候选相邻分区集合为Ctree ={Seg5,Seg6;Seg3,Seg5;Seg1,Seg2}，可判定分区对Seg5,Seg6与Seg1,Seg2应采用斯坦纳树方法部署中继节点以重建连通；其它分区组依然保留启发式部署方法实现与区域中心O的连通。

最后，由于Seg3的相邻分区Seg5与中心O的连通拓扑已经改变，所以需在分区Seg3与中心O的路径上继续部署中继节点，从而实现所有分区的连通。结果分区连通拓扑如图3（e）。

4　仿真分析

通过与1C-SpiderWeb的对比实验，论文将评测CRATST算法的效率，稳定性，功耗性能。其中，通过计算部署中继节点数量评估算法效率。稳定性通过平均节点度来衡量。平均节点度等于恢复后的网络拓扑中能够直接通信的无线链路数量除以部署的中继节点数量。平均节点度越高，表明恢复后的网络稳定越好，节点能量消耗越可能趋于均衡。功耗性能可通过通信跳数来判断。通信跳数为所有分区间相互通信一次所需的总跳数。对于双向通信，各取值双倍累加即可。

实验采用Matlab软件进行模拟。设定目标区域A为1 000 m×1 000 m的正方形区域，并且设定不同的分区数量Nseg和通信半径R。其中，分区数量Nseg取值变化从4到7，通信半径R取值从40 m到120 m每隔20取值一次，共计20种场景。分区位置在目标区域中随机生成，仿真结果均为每种场景随机生成30次网络拓扑得到的均值。

4.1中继节点数量

为了验证CRATST算法的高效性，图4统计了CRATST与1C-SpiderWeb算法在20种场景中网络恢复连通所需中继节点数量。

实验结果如图4所示，给定通信半径R和分区数量Nseg，CRATST算法所需中继节点数量小于1C-SpiderWeb算法。其原因在于，和1C-SpiderWeb算法仅在启发式部署阶段进行的单次优化相比，CRATST算法分别在启发式部署和斯坦纳部署阶段，进行了二次优化。当给定分区数量Nseg，随着通信半径R的增加，相对于1C-SpiderWeb，在CRATST中由路径长度减少带来的高效优势不再明显，在图中则体现为：随R取值的增大，CRATST与1C-SpiderWeb所需中继节点数量越来越接近。

4.2平均节点度

为了验证CRATST算法的稳定性，图5统计了CRATST与1C-SpiderWeb算法在20种场景中网络恢复连通后的平均节点度。

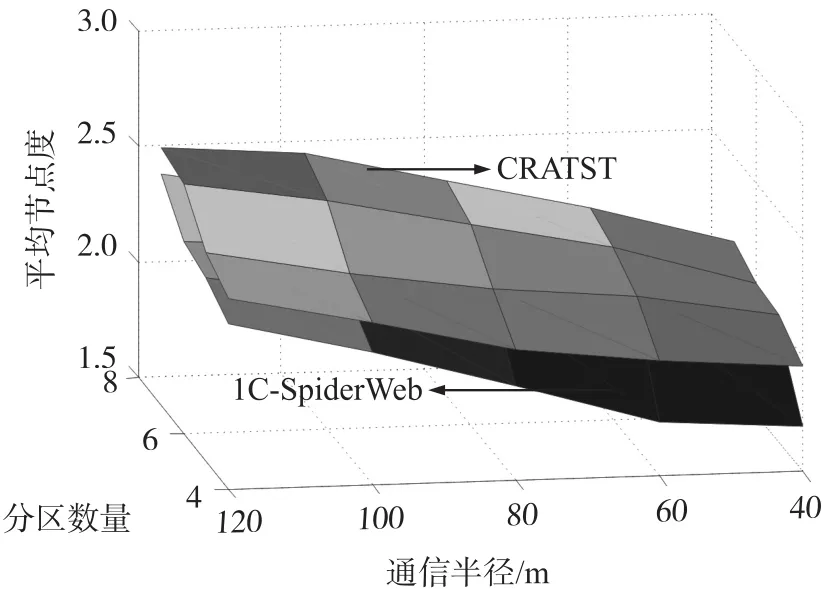
图5　平均节点度随R和Nseg变化图

实验结果如图5所示，给定通信半径R和分区数量Nseg，1C-SpiderWeb算法以大量的中继节点为代价恢复分区连通性，导致其平均节点度降低。因此，CRATST算法网络拓扑的平均节点度要高于1CSpiderWeb算法。当分区数量Nseg一定，随通信半径R增加，2种算法的平均节点度随之增加。这是因为通信半径R增加，更多节点成为邻居节点。但CRATST算法的平均节点度始终高于1C-SpiderWeb算法，说明CRATST算法形成网络稳定性更好。

4.3通信跳数

为了验证CRATST算法的低功耗性，图6统计了CRATST与1C-SpiderWeb算法在20种场景中网络恢复连通后的通信跳数。

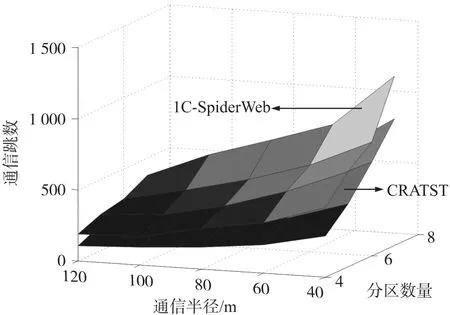
图6　通信跳数随R和Nseg变化图

实验结果如图6所示，给定通信半径R和分区数量Nseg，所有分区间进行一次网络通信，CRATST算法的跳数比1C-SpiderWeb算法要少，其原因在于CRATST算法通过两次优化利用较少的中继节点恢复分区连通性。而通信跳数的减少，说明CRATST算法相对于1C-SpiderWeb算法能够有效减少能量消耗，延长网络寿命。

5　结束语

论文提出基于三角形斯坦纳树的分区连通性恢复算法（CRATST）。算法在部署中继节点的过程中，进行了启发式和斯坦纳部署的两次优化，最大化地减少了中继节点的数量，完成网络连通性的恢复。

实验从中继节点数量、平均节点度和通信跳数三个方面入手，分别分析了算法效率、稳定性、功耗性能。通过与已有算法进行对比实验，发现CRATST

在使用较少中继节点的情况下，生成的网络拓扑在效率、稳定性、功耗性方面具有更好的性能。

参考文献：

［1］Younis M，Senturk I F，Akkaya K，et al. Topology Management Techniques for Tolerating Node Failures in Wireless Sensor Net⁃works：A Survey［J］. Computer Networks，2013，58（2）：254-283.

［2］Al-Turjman F M，Hassanein H S，Waleed M A，et al. Optimized Relay Placement for Wireless Sensor Networks Federation in Envi⁃ronmental Applications［J］. Wireless Communication and Mobile Computing，2011，11（12）：1677-1688.

［3］马晨明，王万良，洪榛.异构无线传感器网络中基于CDS树的拓扑控制方法［J］.传感技术学报，2014，27（6）：814-820.

［4］Lee S，Younis M. Optimized Relay Node Placement for Connect⁃ing Disjoint Wireless Sensor Networks［J］. Computer Networks，2012，56（12）：2788-2804.

［5］Senel F，Younis M. Relay Node Placement in Structurally Dam⁃aged Wireless Sensor Networks via Triangular Steiner Tree Ap⁃ proximation［J］. Elsevier Computer Communications，2011，34 （16）：1932-1941.

［6］Senel F，Younis M. Optimized Relay Node Placement for Estab⁃lishing Connectivity in Sensor Networks［C］//Global Communica⁃tions Conference（GLOBECOM），Anaheim，CA，December 2012：512-517.

［7］Lee S，Younis M，Lee M. Connectivity Restoration in a Partitioned Wireless Sensor Network with Assured Fault Tolerance［J］. Ad Hoc Networks，2015，24（24）：1-19.

［8］陈洪生，石柯.基于四边形斯坦纳树的无线传感器网络连通恢复［J］.计算机学报，2014，37（2）：457-468.

［9］杨洪，许力，章静.无线传感器网络中容错虚拟骨干网构造算法［J］.小型微型计算机系统，2014，35（12）：2612-2616.

［10］Joshi Y K，Younis M. Mobility-Based Internetworking of Disjoint Segments［C］//Communications（QBSC），2014 27th Biennial Sym⁃posium on IEEE，Kingston，ON，2014：193-197.

［11］Younis M，Lee S，Abbasi A A. A Localized Algorithm for Restor⁃ing Inter-Node Connectivity in Networks of Moveable Sensors［J］. IEEE Transactions on Computers，2010，59（12）：1669-1681.

［12］Lloyd E L，Xue G. Relay Node Placement in Wireless Sensor Net⁃works［J］.IEEETransactions on Computers，2007，56（1）：134-138.

［13］Senel F，Younis M，Akkaya K. A Robust Relay Node Placement Heuristic for Structurally Damaged Wireless Sensor Networks ［C］//Proceedings of the LCN’09，Zurich，Switzerland，Oct. 2009：633-640.

［14］Lee S，Younis M. Optimized Relay Placement to Federate Seg⁃ments in Wireless Sensor Networks［J］. IEEE Journal on Selected Area in Communications，Special Issue on Mission Critical Net⁃working，2010，28（5）：742-752.

［15］张会新，陈德沅，彭晴晴，等.一种改进的TDOA无线传感器网络节点定位算法［J］.传感技术学报，2015，28（3）：412-415.

［16］Cheng X Z，Du D Z，Wang L S，et al. Relay Sensor Placement in Wireless Sensor Networks［J］. Wireless Networks，2008，14（3）：347-355.

［17］Lin G H，Xue G. Steiner Tree Problem with Minimum Mumber of Steiner Points and Bounded Edge-Length［J］. Information Process⁃ing Letters，1999，69（2）：53-57.

秦宁宁（1980-），女，江南大学副教授，研究方向为无线传感器网络覆盖，ningning801108@163.com；

吴德恩（1988-），男，江南大学硕士研究生，研究方向为无线传感器网络连通性修复，1004995682@qq.com；

余颖华（1989-）女，江南大学硕士研究生，研究方向为无线传感器网络覆盖，yuyinghuahn@163.com。

Connectivity Recovery Algorithm in Partition Based on Triangle Steiner Tree*

QIN Ningning1，2*，WU Deen1，YU Yinghua1
（1.School of Internet of Things Engineering，Jiangnan University，Wuxi Jiangsu 214122，China；2.Key Laboratory of Advanced Process Control for Light Industry Ministry of Education，Jiangnan University，Wuxi Jiangsu 214122，China）

Abstract：Due to the consumption of energy as well as the impact of other external factors，nodes in wireless sensor networks（WSN）can easily encounter the problem of large-scale failure，thus getting the networks divided into sever⁃al independent partitions which can’t effectively communicate with each other. In order to restore the network and reconstruct the communication links between the partitions，a triangle steiner tree based connectivity restoration al⁃gorithm is proposed. The algorithm first employs a traditional algorithm to achieve partition connectivity，and then by constructing triangle Steiner tree the number of deployed relay nodes can be reduced. Compared with some exist⁃ing algorithms，the topology of the network formed in this article can not only reduce the number of deployed relay nodes and make the partitions reconnected，but also is able to cut down the energy consumption of network commu⁃nication. The simulation results altogether indicate the proposed algorithm is more effective than traditional meth⁃ods in buildingthe network topology.

Key words：wireless sensor network；connectivity；triangle steiner tree；partition

doi：EEACC：6150P10.3969/j.issn.1004-1699.2016.03.020

收稿日期：2015-09-21修改日期：2015-10-27

中图分类号：TP393

文献标识码：A

文章编号：1004-1699（2016）03-0423-06