相位差方法校正多通道AD采集高精度时间误差

2016-05-03广州大学罗高涌蔡李志

电子世界 2016年7期

广州大学　黄　磊　罗高涌　蔡李志

广州大学黄磊罗高涌蔡李志

【摘要】在多通道接收机同步AD采集系统中，多个接收通道之间同步时间差会带来采样数据的相位差。这一误差在时间敏感的系统中是不允许存在的。本文提出通过反正弦变换原理提取正弦信号相位差校正微小时间误差的方法。并对采样噪声和不精确度进行了分析和处理。实现了低成本、高精度同步时间校准。校正多通道时间的精度在1ns以内。并对理论进行了工程实测，符合理想数据。

【关键词】反正弦；高精度；同步；相位差

0　前言

笔者在设计一套基于扩频通信的室内定位系统时，建立三基站同步接收待定位点的BPSK调制信号，通过自相关的运算和相位差提取时间差的算法获得信号到达三个基站的时间差。利用TDOA算法就可以实现室内定位。在理论仿真中，该算法平均定位误差在1cm以内。在实际测试中，笔者发现AD采集系统下各个采集通道会有20-50ns的不同步采样延时，不能做到精准同步采样模拟信号，这一误差对于室内定位系统的影响是巨大的，无法达到理论上的1cm时间精度。基于此，笔者设计了一种校正多通道接收机不同步误差的算法。

此外，雷达[1]地震数据的采集[2]，水声工程领域，雷达动目标的检测[3]，基站同步等领域方面，其主要技术手段就是使用多通道的天线或接收机对同一无线信号进行同步接收。多通道同步均具有重要作用。如果不能保证基站和系统间的精准时钟同步将导致系统内严重的互干扰甚至影响全系统正常工作[4]。在目前现有的时间同步方案，有通过GPS授时实现基站同步[5]，虽然时间精准，但成本较大。文献[6]通过IEEE1588V2协议方式实现LTE基站同步，其精度依赖于计数器频率准确性和链路的对称性，对传输设备性能和网络的要求较高。文献[7]提出的以太网实现同步，实时性差。本文提出基于提取多通道相位差的方法，计算时间差信息。由于在中频信号中频频率f较大，相位具有放大ns级微小时间的功能。这也是本文高精度原理所在。该方法方法也存在一定的局限性，受量化噪声影响较大，需要增加软件去噪环节。但是具有实施成本小，具有实时性高，时间精确等优点。在测量相位差的方法中，文献[8]数值取样法软件部分简单，易于实现，但是在被测频率较高时误差较大。过零鉴相法[9]具有测量分辨率高，线性好，易数字化的优点，但是易受实际电子元器件的影响，做到精准测量相位很难。DFT算法具有运算速度快，实时性好的特点，但初相位估计精度取决于接收信号的时间长度相关，DFT的估计精度受到限制，时间过长，又会给实时处理带来困难。[10]相位信息普遍用于工程等各方面领域。相位差测量在故障诊断[11]，电网中电压与电流相位差的准确测量[12]，流体质量的高精度测量[13]等领域都有中亚的应用。

本文提取相位差方法是采用基于采样点做反正弦变换的方法。具有运算量小的特点，并通过对信号的一系列预处理，能够克服采样点受采样误差影响大，采样点数少等不利因素。实现高精度时间的提取，其误差在1ns以内。

1　理论介绍

设正弦信号同时输入CH1，CH2通道进行AD采样，分别得到两路具有同频率不同相位差的信号。以CH1通道采集到的信号作为时间基准(即零相位信号)

通过反正弦公式：

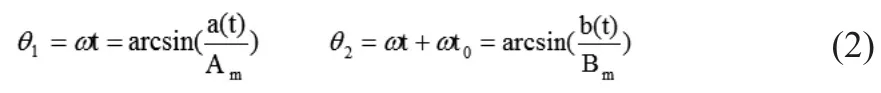
相位图形如图1所示。

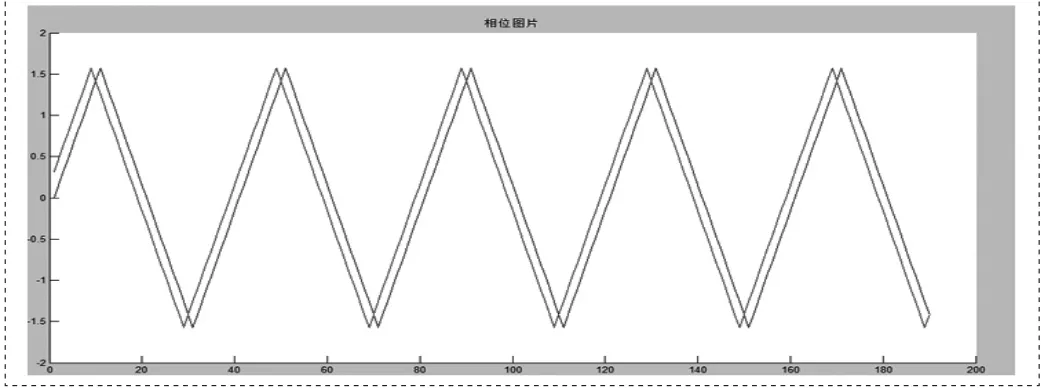
图1　θ1，θ2

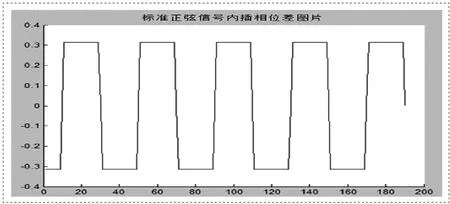
图2　△θ

现已知输入频率，再通过相位与时间的关系，求得时间差。这个时间差即是CH1通路与CH2通路先后采样的时间差t0。

相位与时间差的关系如下：

f为输入信号的频率。

2　AD采样噪声分析

进行A/D采样时，会引入量化噪声，另外实际电路中还有热噪声、霰弹噪声和闪烁噪声等。这些噪声最终都会叠加到中频测试信号上，对中频测试信号的相位测试不确定度产生影响。实际上，如果某种噪声比实际考虑的有用频带宽得多的范围内具有比较“平坦”的功率谱，就可以把它当作白噪声来处理。而上述的各种噪声满足白噪声的特征，因此这里统一将上述噪声作为白噪声处理。

量化噪声是由于直流信号转换具有量化达1/2LSB(LSB为AD采样满量程输入的最小单位)所以数据采样具有量化噪声。一个理想的常规N位ADC的采样量化噪声有效值为q/12，均匀分布在奈奎斯特频带直流至fs/2范围内。其中q为LSB的权重，fs为采样频率的误差，分布在0～fs/2之间的随机噪声，这就是量化噪声。下面结合热噪声和量化噪声研究功率谱与采样噪声的关系。

热噪声功率为[14]

K为玻尔兹曼常数，B为被测对象的噪声带宽，T为被测对象工作温度，NF为被测对象噪声系数。

AD量化噪声功率可表示为：

因此信噪比可表示为：

则相位测量精度可表示为[15]：

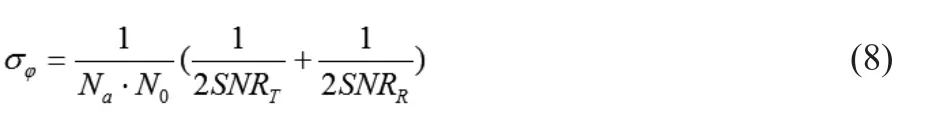
其中，Na为多次测量累计平均次数，分别为两路测量信号的信噪比。其信噪比和不确定度与ADC的分辨率N有关系。

因此在AD采样器分辨率固定的情况下，文中使用内插滤波法以较低的采样分辨率和很高的采样速率增加有效分辨率。由DFT的Parseval定理：

可知信号在一个域及其对应的变换域中满足能量守恒原理。上式说明信号在时域总能量等于其频域总能量。而其功率谱密度在经过N点内插零点后。

理想正弦信号经过DFT变换到频域后，只有基波谱线信号有能量，其余谱线的能量均为零，也就是说理想正弦信号的能量不会随着采样点数的变化而变化。而随着采样点数的增加，在采样带宽内噪声总能量一定的情况下，随机噪声的每条谱线的能量会逐渐减小，若采样点数为N，则每条谱线的能量是采样带宽内噪声总能量的1/N，其中只有叠加到理想正弦信号上的部分对相位计算有影响。

也就是说，N点DFT变换本身隐含着对噪声能量有统计平均效应，随着采样点数的增加，经过DFT变换，叠加到中频测试信号上的噪声能量会减小[16]。因此，本文通过在ADC之后重采样内插零点，添加数字滤波器，滤除信号主频至Kfs/2之间能量见效的无用信号，而又不影响有用信号，从而提高了信噪比，实现了用低分辨率ADC达到高分辨率的效果。使总信噪比增加。如图3所示。

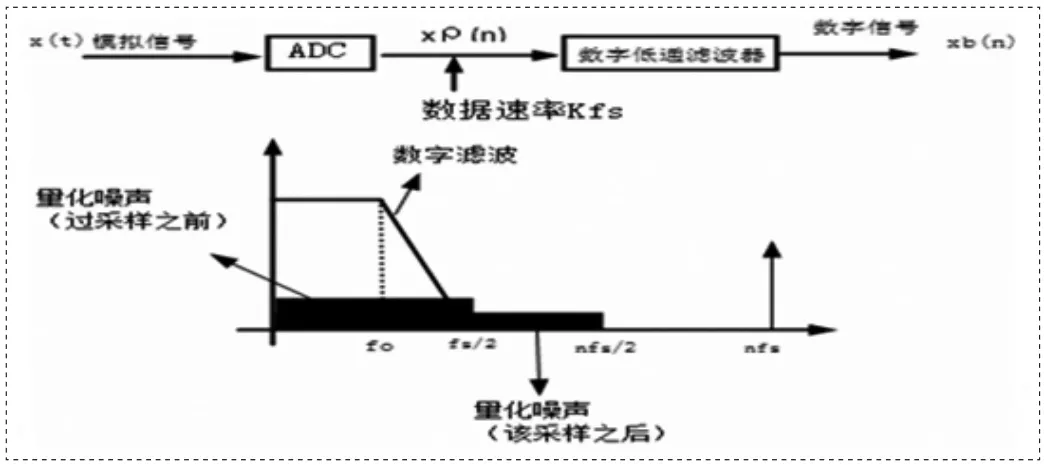
图3　量化噪声滤波频谱图

3　系统实现与测试效果

3.1 系统实现（见图4）

利用正弦信号发生器分别向CH1，CH2通道接入1MHZ，10MHZ正弦信号。采样器采样频率为fs=40MHZ。采样精度14位。满幅值为95%。以Matlab作为数据处理平台对采集数字信号进行处理和验证。

在信号理论中，对序列x(n)进行整数倍内插,相当于对原序列在时域进行扩展，在频域上有1/L倍的比例缩放。由于采样率的增加，在新信号xb(n)的频谱中不仅包含x(n)的基带频谱，还包含这个频谱的周期重复，必须采用低通滤波器h(n)来滤除这些重复的镜像，保证输出信号xb(n)中仅包含原信号的基带频谱。此时再通过合适的低通滤波器后会得到还原效果较好的正弦波信号[17]。

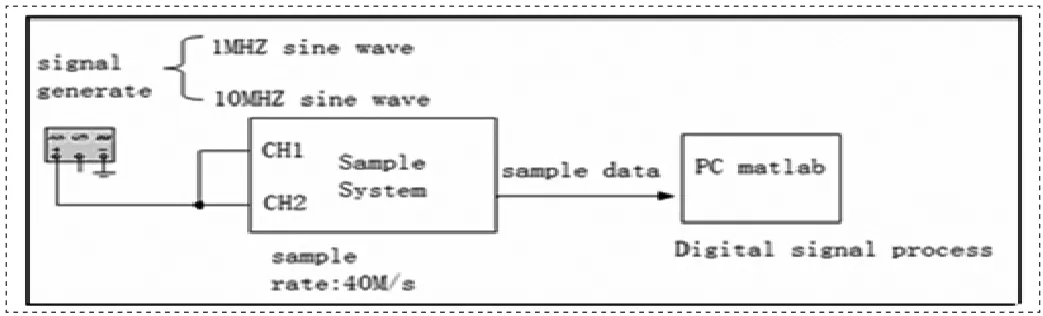
图4　系统流程图

若设原始采样序列为x(n)，则经过内插后组成一个新的序列xρ(n)：

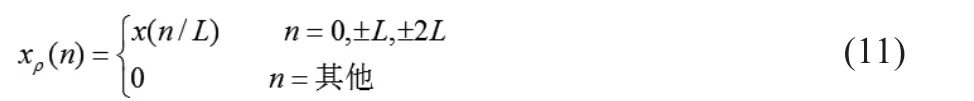
内插器输出信号xρ(n)的Z交换为：

将xρ(n)通过一个截止频率为ω=π/L的低通滤波器，经滤波后这些插进的零值点将不再是零，从而得到插值后的输出信号xb(n)[18]。

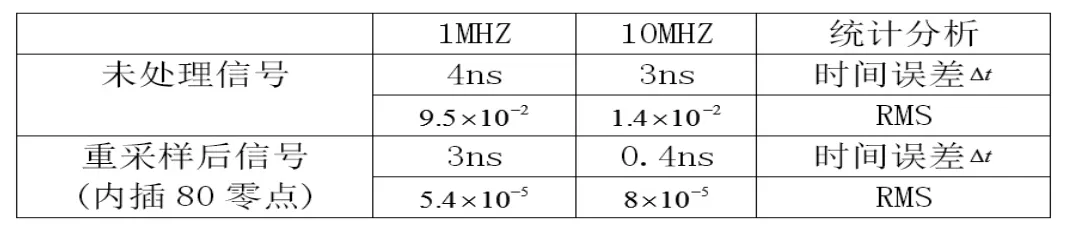
表1

从接近实用角度考虑，本文随机选取内插80个零点，利用阶数适中的5阶butterworth分别对1MHZ，10MHZ信号进行处理。Butterworth滤波器相比FIR滤波器具有在通带和阻带都有平坦的幅频响应，虽然IIR滤波器会原始信号相位，但是并不影响其相位差。且从通带两边中心向两边的幅频幅频响应单调下降，在实际模拟电路中和数字滤波器设计易于实现。增大点数后的正弦波信号较原来采样点数少的信号相比，增采样效果好，计算时间差波动如表1所示。

经过重采样和滤波增加采样分辨率后，10MHZ信号的波动较小，从原来的10-2数量级降为现在的10-5数量级，时间差别在1ns以内。而1MHZ信号波动虽然也有效减小，但是频谱如图4(左)所示，并没有如期望将量化噪声和白噪声彻底滤掉，因此仍然有3ns的时间误差存在。内插80个零点对于信号x(t)的傅里叶变换有。信号频谱尺度变为原来的1/80，量化噪声和白噪声与正弦波谱距离近，给滤波带来困难：若截止频率过高，杂波频谱没有衰减；若截止频率过低，会影响信号频谱有效值，因此在频谱上杂波成分一直存在。无法得到理想结果。

3.2 不同频率信号还原效果差异分析

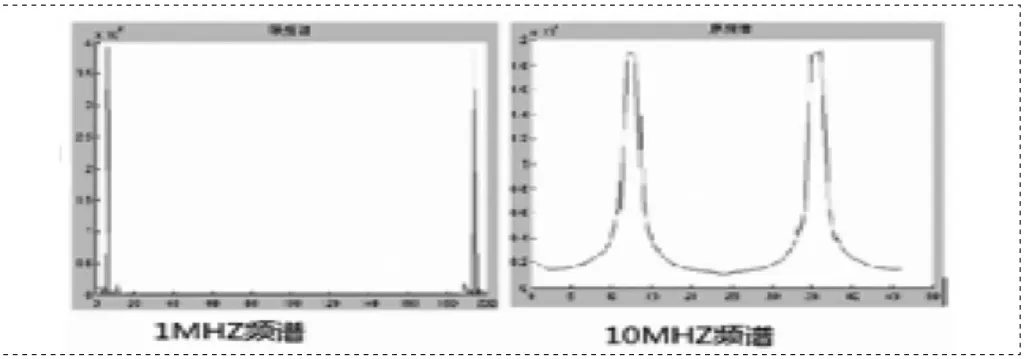
图5　不同频率频谱图

输入10MHZ与1MHZ都经过相同的处理方式，但是10MHZ的波形还原效果以及计算出的时间误差更为精准。是由于40MHZ采样器对1MHZ原始信号进行过采样增加采样噪声。如图5所示，1MHZ频谱采样噪声比10MHZ采样噪声大。在重采样的过程中，也将噪声频谱周期性幅值。因此在相同的滤波条件下下，计算的相位差精确度1MHZ信号没有10MHZ信号精确。

3.3内插零点的选择

适当的选择内插点数可以减少软件成本，降低滤波难度。内插N点，频谱尺度会以1/N变换。内插点数越高，要想获得较好的频谱，需要选频效果更加接近理想的低通滤波器。因此笔者用相同阶数，适当截止频率的butterworth滤波器对内插不同点数的信号进行多相滤波，通过相位差的波动程度来说明内插点数对还原波形效果和时间精度的影响。在上节的论述中，10MHZ信号已获得较好的频谱和滤波效果，因此对未处理好的1MHZ信号进行测试。表2为不同内插点数预处理后时间差波动，表3为对应频谱。

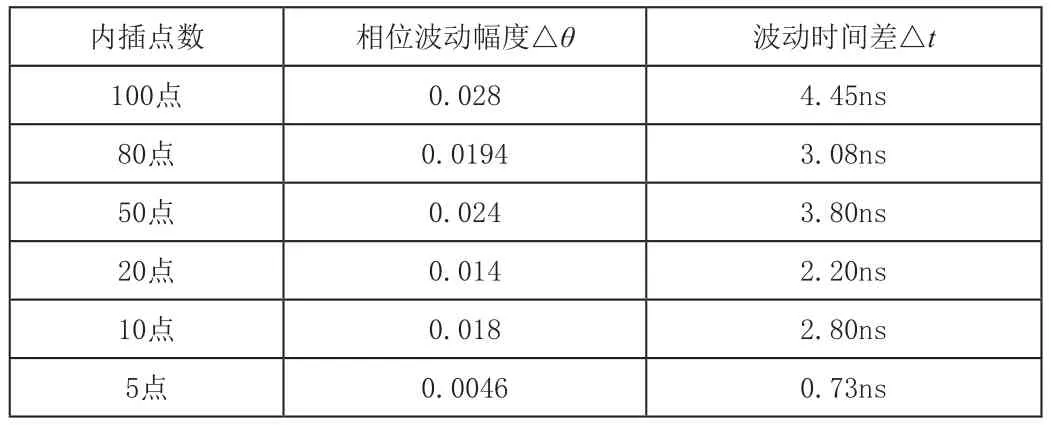
表2

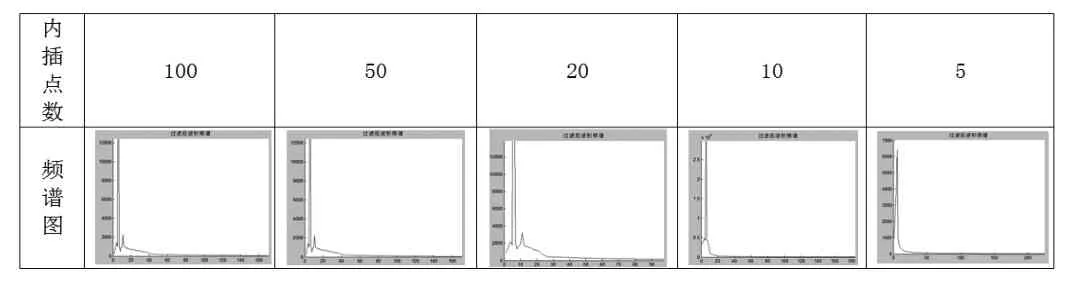
表3

由表2，3，在内插点数为100,50时，杂波成分和正弦波主频成分始终无法滤除，要想滤掉杂波需要提高该滤波器阶数，或者换更为理想的滤波器。内插点数为10时能够对载波之外噪声有大的衰减，内插点数为5的情况下能完全滤掉杂波，获得相位差波动最小的结果。所以只要能够满足我们实际工程项目中的需求的适当重采样，进行合适的滤波符合项目需求即可。

4　总结与展望

本文论述了一种校正多通道相位差的数字提取方法，并能够识别出恒定的时间误差。通过选择选取适当的内插点数和截止频率的多相滤波使得误差在1ns以内。为多接收机的同步机制带来一种时间精度高的同步技术。由于采用了全数字处理方法,使得系统复杂度和成本大大降低，避免了通过原子钟授时等较为复杂的方法。可用于多通道接收测向领域,具有一定参考和推广价值。

参考文献

[1]王亚涛.扩频系统多通道相位差测量技术[J].电讯技术,2010-08: 92-96.

[2]王瀛.同步时间差和小相位差计算引起的相位差分析[J].信息与电脑(理论版),2011,10:171.

[3]李永丽.多通道高速数据采集及大容量存储系统设计[D].西安电子科技大学,2009.

[4]闫震,史楠.LTE基站同步方式浅析[J].信息通信,2014,11: 211-212.

[5]程利娟.无线传感器网络时间同步算法研究[D].西北工业大学,2007.

[6]张海涛,涂亚庆.计及负频率影响的科里奥利质量流量计信号处理方法[J].仪器仪表学报,2007,03:539-544.

[7]沈国重.多抽样率信号处理方法及其在实时系统中的应用[D].浙江大学,2001.

[8]马利人,申莉,傅士冀.高精度工频相位计的研制[J].电测与仪表,2006,01:42-44+37.

[9]李永坚,黄绍平,浣喜明.基于相关分析法和虚拟仪器技术的相位测量[J].计量技术,2004,11:9-11.

[10]秦爽.多通道同步数据采集系统设计与实现[D].电子科技大学,2009.

[11]蒋鑫,芮鹤龄,杜艳艳.TD-SCDMA家庭基站时钟同步解决方案的研究[J].电信科学,2009,04:25-28.