基于自回归模型和超球面支持向量机的局部放电模式识别

张建文， 王恩俊， 陈焕栩， 王 曼， 丁 冬

1. 中国矿业大学信息与电气工程学院， 江苏 徐州 221008;2. 中船黄埔文冲船舶有限公司， 广东 广州 510715)

基于自回归模型和超球面支持向量机的局部放电模式识别

张建文1， 王恩俊1， 陈焕栩1， 王 曼1， 丁 冬2

1. 中国矿业大学信息与电气工程学院， 江苏 徐州 221008;2. 中船黄埔文冲船舶有限公司， 广东 广州 510715)

为了提高变压器局部放电信号分类的准确率，提出了基于自回归模型和超球面支持向量机的模式识别算法。该方法对不同放电类型的信号建立自回归模型，将得到的模型系数作为局部放电信号的特征矩阵，输入到超球面支持向量机中对局部放电信号进行分类。由于超球面支持向量机中的惩罚因子和核函数参数对分类的准确率起着重要的作用，因此采用粒子群算法寻找最优的惩罚因子和核函数参数的组合。实验结果表明，基于自回归模型的参数特征，采用优化后的超球面支持向量机对局部放电信号进行分类，其分类准确率比未经优化超球面支持向量机的分类准确率提高了13.33%，比BP神经网络的识别率提高了20%，为局部放电信号的模式识别提供了一种新思路。

局部放电信号； 自回归模型； 超球面支持向量机； 粒子群算法

1 引言

局部放电是变压器绝缘劣化的重要原因和表现形式。不同的放电模式具有不同的放电性能，对变压器绝缘的危害程度也有较大不同。因此，进行变压器局部放电模式识别的研究[1,2]，对保证变压器稳定可靠运行具有重要的现实意义。

在局部放电信号的模式识别中，信号特征类型及模式识别算法对最终判别结果影响较大。

对于局部放电信号提取的特征参数有统计特征[3,4]、分形特征[5,6]、放电图像灰度特征[7]和矩特征[8]，它们均被证明具有良好的辨识能力。然而这些特征均是基于PRPD图谱[9]所提取的，PRPD图谱不是直接对局部放电信号提取特征，而是通过对大量的放电信号进行统计来构造基于放电电量-放电相位的二维图谱和基于放电电量-放电相位-放电次数的三维图谱，从而间接地获取局部放电信号特征，由二维图谱和三维图谱可以获得统计特征和三维表列特征，由二维灰度图谱可以获得分形特征，灰度特征和矩特征。由于不是直接对信号进行特征提取，这样会遗漏一些放电信号的信息，不利于局部放电信号的识别，鉴于此，本文尝试采用自回归模型算法对放电信号直接提取特征，这样保证了所提取信号的信息是最原始、最直接的。

对于局部放电的模式识别，人工神经网络和支持向量机等方法在局部放电的分类中得到了广泛应用。人工神经网络是基于大样本理论建立的，一般来说，样本数目越多，识别效果越好。然而对于局部放电的模式识别，由于制作放电样本的数目是有限的，若采用BP神经网络[10,11]识别局部放电类型，平均识别率能够达到85%，识别率较低。支持向量机[12]是建立在结构风险最小化原则上的一种统计学习模型,其在解决小样本、多种类模式识别问题上占据较多的优势，它的目标是在有限样本的情况下，能够得到较高的识别率，是兼顾经验风险和置信范围的一种思想。支持向量机应用在多个领域，都取得了较好的识别效果，然而局部放电信号特征的分布是不均匀的，经典的超平面支持向量机很难对样本进行准确分类，而超球面支持向量机[13,14]能找到包含某类样本在内的由支持向量支撑的最小超球面，将样本用超球定界，需要的样本集小，分类精度高。因此，本文基于自回归模型算法提取局部放电信号的特征，采用最优超球面支持向量机对局部放电信号进行分类。

2 局部放电信号的特征提取

对局部放电信号进行自回归模型参数估计，如式 (1) 所示：

(1)

式中，ak表示第k个自回归模型参数；v(t)为模型的残差，是均值为零、方差为σ2的白噪声序列；p为模型的阶数。

本文采用日本统计学家Akaike提出的AIC准则[15]来确定模型的阶数p，采用BURG算法[16]确定参数ak，并使ak作为局部放电信号的特征，构成特征向量矩阵。

3 局部放电信号的分类

3.1 超球面支持向量机

对于k>2的分类问题，数学描述为：给定n维空间的集合Am，m=1,2，…,k，每个集合包含lm个样本点，i=1,2，…,lm，对每个集合寻找一个超球(am,Rm)，am为球心，Rm为球半径，并使球半径尽量小，使得该最小超球尽可能包含所有的同类样本点xim。考虑到存在一些孤立点(离球心较远的样本)，应允许这些点落在超球面外，则寻找最小超球的过程可演化为原始的优化问题：

(2)

式中，ξim为松弛变量；C为惩罚因子，控制对错分样本的惩罚程度，实现在超球大小和错分样本数量之间的折衷。

超球面支持向量机的球心为[13]：

(3)

球半径的平方为：

(4)

式中，aim、ajm为Lagrange乘子；xm为第m类样本的任意一个支持向量；K(·,·)为核函数。

在超平面支持向量机中，高斯核函数的训练效果要优于线性核函数和Sigmoid核函数[12]，因此在超球面支持向量机中也采用高斯核函数，如式 (5) 所示：

(5)

式中，δ为高斯核函数的参数，它影响着样本数据在特征空间中的分布复杂度和支持向量之间的关联度。

则可知待测样本y到球心之间距离的平方为:

(6)

最后D2与(Rm)2进行比较，即

(7)

式中，最小值a对应的k就是待测样本所属的类别。

3.2 粒子群优化算法

超球面支持向量机的分类性能是由惩罚因子和核函数参数共同决定的，如图1所示。可以看出，不同的参数组合会得到不同的超球面支持向量机分类器，其分类精度也会有较大的差异，因此，寻找一组最优的惩罚因子和核函数参数组合，构成最优超球面支持向量机，有利于提高分类准确率。由于粒子群优化算法在多个领域表现了其优异的寻优性能[17-19]，故本文采用粒子群算法来寻找最优的超球面支持向量机。

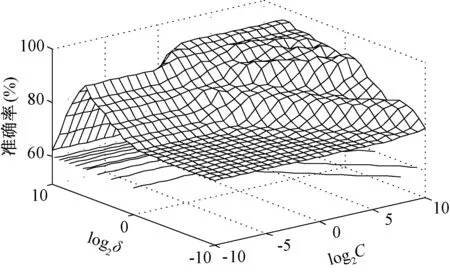
图1 超球面支持向量机参数与其分类精度的关系Fig.1 Relationship of hypersphere support vector machine parameters and its classification accuracy

粒子群优化算法的原理见文献[20]，本文在此不再赘述。本文中惩罚因子C的取值范围为[1/N,1],N为样本的采样信号个数，核函数参数δ的取值范围为[0.001,1000]；w=0.729，c1=c2=1.494；本文设置进化迭代数t=100，种群规模数m=20。

本文选取5折交叉验证分类准确率作为粒子群寻优算法的适应度函数，其表达式为：

(8)

式中，ei为第i次交叉验证分类准确率；k为交叉验证折数；ηe为正确分类样本数；η为总样本数。因此，faccuracy值越大，识别准确率越高，则分类效果越好。

4 基于AM-HSVM的模式识别

局部放电信号模式识别的具体步骤如图2所示。由AIC准则确定自回归模型阶数p，然后利用BURG算法求得每个信号的自回归模型参数，这样就会得到不同放电类型的特征向量矩阵：

(9)

式中，N为每种放电类型信号的个数。

图2 基于自回归模型和超球面支持向量机的局部放电模式识别流程图Fig.2 Partial discharge pattern autorecognition flowchart based on autoregression model and hypersphere support vector machine

将训练的特征向量矩阵输入到超球面支持向量机中，并将5折交叉验证准确率作为适应度函数开始进行粒子群优化，最终会得到最优的参数组合(C,δ)。将该参数组合与超球面支持向量机构成最优超球面支持向量机，利用该向量机对测试样本进行分类。

5 实验验证

试验在高压实验室中搭建的局部放电实验平台上进行，局部放电试验电路图如图3所示。其中，T1为接触调压器(50kV·A，0～400V)；T2为无晕试验变压器(50kV·A，50kV)；C1为电容分压器高压臂；C2为电容分压器低压臂；Ck为耦合电容(990pF)；Cx为试品；R为保护电阻(5kΩ)；Zm为检测阻抗；A为放大器。采用的示波器为安捷伦Infiniium系列示波器，其频率带宽为500MHz且采样率高达1GS/s。

图3 局部放电试验电路Fig.3 Partial discharge tentative circuit

实验室中制作了三种典型的局部放电试验模型，如图4所示，图4(a)为固体绝缘内气隙放电模型，图4(b)为油中电晕放电模型，图4(c)为油中沿面放电模型。

图4 局部放电试验典型模型Fig.4 Typical models of partial discharge tentative

本文制作每种局部放电类型的样本各10个，总共30个样本，每个样本采集50个工频周期的局部放电信号。采样频率为1MHz，背景噪声为20mV。表1为不同类型局部放电的试验条件。

表1 局部放电的试验条件Tab.1 Test conditions of partial discharge

表2～表4分别为气隙放电、电晕放电和沿面放电的5个放电信号的自回归模型参数。

表2 气隙放电的自回归模型参数Tab.2 Autoregression model parameters of gap discharge

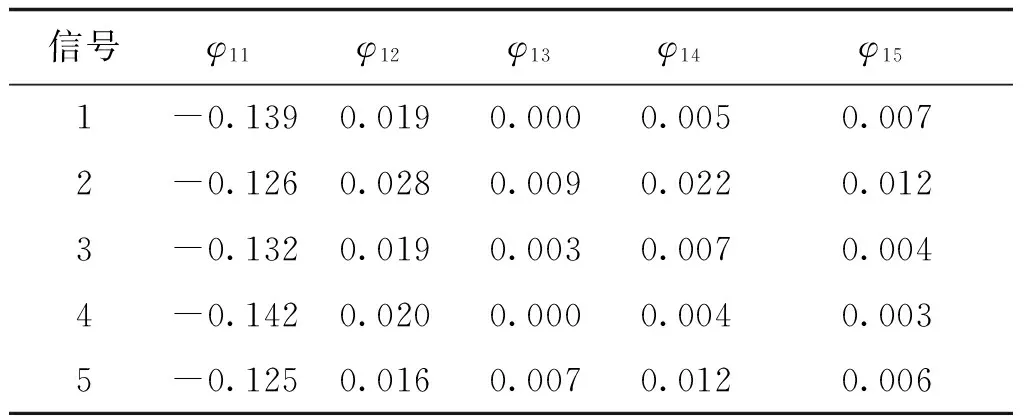
表3 电晕放电的自回归模型参数Tab.3 Autoregression model parameters of corona discharge

表4 沿面放电的自回归模型参数Tab.4 Autoregression model parameters of creeping discharge

为了更好地进行训练和识别，将特征向量矩阵进行归一化处理，然后将归一化的特征向量矩阵输入到超球面支持向量机中进行训练，并利用粒子群优化算法寻找最优的参数组合(C,δ)，寻优过程如图5所示。

图5 准确分类率适应度值Fig.5 Fitness value of accurate classification rate

由图5可知，在粒子群寻优过程中，其平均适应度值维持在85%左右，并且28代及以后最佳适应度值保持稳定，其值为100%，说明有较高的识别率，此时最优的参数组合为(0.132,377.302)。

将超球面支持向量机的惩罚因子设置为0.132，核函数参数设置为377.302，构成最优超球面支持向量机。利用该支持向量机对测试样本进行识别分类，并将分类结果与未经优化的超球面支持向量机和BP神经网络的分类结果进行比较，如表5所示。

表5 不同分类器的分类结果比较Tab.5 Classification results comparison of different classifiers

由表5可知，对于BP神经网络,其局部放电的平均识别率为80%,对于未经优化的超球面支持向量机，其局部放电的平均识别率为86.67%，而经过粒子群优化的超球面支持向量机，其局部放电的平均识别率达到了100%，识别准确率比神经网络提高了20%，比未经优化的超球面支持向量机提高了13.33%。

6 结论

本文首次将自回归模型参数特征应用于局部放电的模式识别中，构成局部放电信号的特征向量矩阵，然后将其输入到经过粒子群优化的超球面支持向量机中进行模式识别，并将识别结果与BP神经网络和未经优化的超球面支持向量机的识别结果进行比较，其识别的准确率分别提高了20%和13.33%。由此可知，基于自回归模型系数，采用最优超球面支持向量机的局部放电模式识别算法对局部放电信号的分类具有一定的指导意义。

[1] 郭少朋, 韩 立, 徐鲁宁, 等 (Guo Shaopeng, Han Li, Xu Luning, et al.). 光纤传感器在局部放电检测中的研究进展综述 (Review of research on fiber optic sensors for partial discharge detection) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2016, 35(3): 47-53.

[2] 李延沐, 袁 鹏, 牟 磊, 等 (Li Yanmu, Yuan Peng, Mou Lei, et al.). 基于自适应神经模糊推理系统(ANFIS)的变压器超高频局部放电模式识别 (Partial discharge of UHF pattern recognition in transformers using adaptive neuro-fuzzy inference system (ANFIS)) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2005, 24(4): 30-33.

[3] 苑津莎, 尚海昆 (Yuan Jinsha, Shang Haikun). 基于主成分分析和概率神经网络的变压器局部放电模式识别 (Pattern recognition based on principal component analysis and probabilistic neural networks for partial discharge of power transformer) [J]. 电力自动化设备 (Electric Power Automation Equipment), 2013, 33(6): 27-31.

[4] 胡文堂, 高胜友,余绍峰, 等 (Hu Wentang, Gao Shengyou, Yu Shaofeng, et al.). 统计参数在变压器局部放电模式识别中的应用 (Application of statistic parameters in recognition of partial discharge in transformers) [J]. 高电压技术 (High Voltage Engineering), 2009, 35(2): 277-281.

[5] 崔晓慧 (Cui Xiaohui). 基于分形特征和统计特征的矿用高压电缆人工缺陷局部放电模式识别方法的研究 (Pattern recognition of partial discharges based on fractal features and statistical features regarding mine high voltage cables with artificial defects) [D]. 太原: 太原理工大学 (Taiyuan: Taiyuan University of Technology), 2014.

[6] 杨眉 (Yang Mei). 基于统计和分形特征的油纸绝缘局部放电模式识别研究 (Research on pattern recognition of PD in oil-paper insulation based on statistical and fractal feature) [D]. 重庆: 重庆大学 (Chongqing: Chongqing University), 2006.

[7] 唐炬, 魏钢, 李伟, 等 (Tang Ju, Wei Gang, Li Wei, et al.). 基于双向二维最大间距准则的局部放电灰度图像特征提取 (Partial discharge gray image feature extraction based on bi-directional two-dimensional maximum margin criterion) [J]. 电网技术 (Power System Technology), 2011, 35(3): 129-134.

[8] 杜杰, 程瑛颖, 周峰, 等 (Du Jie, Cheng Yingying, Zhou Feng, et al.). 油纸绝缘沿面放电小波矩特征信息提取及其过程划分 (Wavelet moment features extraction of surface discharge signals on oil-paper insulation and partition of the discharge process) [J]. 高压电器 (High Voltage Apparatus), 2015, 51(1): 61-66.

[9] 刘通, 薛永刚, 赵煦, 等 (Liu Tong, Xue Yonggang, Zhao Xu, et al.). 变压器内单一局放PRPD谱图统计参量的主成分分析 (Principal component analysis for statistical parameters of phase resolved partial discharge spectra of single partial discharge pattern in power transformers) [J]. 南方电网技术 (Southern Power System Technology), 2014, 8(5): 33-37.

[10] 唐炬, 李伟, 欧阳有鹏 (Tang Ju, Li Wei, Ouyang Youpeng). 采用小波变换奇异值分解方法的局部放电模式识别 (Partial discharge pattern recognition using discrete wavelet transform and singular value decomposition) [J]. 高电压技术 (High Voltage Engineering), 2010, 36(7): 1686-1691.

[11] 律方成, 金虎, 王子建, 等 (Lv Fangcheng, Jin Hu, Wang Zijian, et al.). 基于主成分分析和多分类相关向量机的GIS局部放电模式识别 (GIS partial discharge pattern recognition based on principal component analysis and milticlass relevance vector machine) [J]. 电工技术学报 (Transactions of China Electrotechnical Society), 2015, 30(6): 225-231.

[12] 尚海昆, 苑津莎, 王瑜, 等 (Shang Haikun, Yuan Jinsha, Wang Yu, et al.). 多核多分类相关向量机在变压器局部放电模式识别中的应用 (Partial discharge pattern recognition in power transformer based on multi-Kernel multi-class relevance vector machine) [J]. 电工技术学报 (Transactions of China Electrotechnical Society), 2014, 29(11): 221-228.

[13] 唐炬, 林俊亦, 卓然, 等 (Tangn Ju, Lin Junyi, Zhuo Ran, et al.). 基于支持向量数据描述的局部放电类型识别 (Partial discharge type recognition based on support vector data description) [J]. 高电压技术 (High Voltage Engineering), 2013, 39(5): 1046-1053.

[14] 王自营, 邱绵浩, 安钢, 等 (Wang Ziying, Qiu Mianhao, An Gang, et al.). 基于一类超球面支持向量机的机械故障诊断研究 (Fault diagnosis investigation of machine based on one class hyperspherical SVM) [J]. 振动工程学报 (Journal of Vibration Engineering), 2008, 21(6): 553-558.

[15] Hirotugu Akaike. A new look at the statistical model identification[J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716-723.

[16] 李明, 王晓茹 (Li Ming, Wang Xiaoru). 一种用于电力系统间谐波谱估计的自回归模型算法 (An autoregressive model algorithm for the inter-harmonic spectral estimation in the power system) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2010, 30(1): 72-76.

[17] 陈雁, 孙海顺, 文劲宇, 等 (Chen Yan, Sun Haishun, Wen Jinyu, et al.). 改进粒子群算法在船舶电力系统网络重构中的应用 (Application of improved PSO algorithm in network reconfiguration of shipboard power system) [J]. 电力自动化设备 (Electric Power Automation Equipment), 2011, 31(3): 29-39.

[18] 李鹏, 李涛, 张双乐, 等 (Li Peng, Li Tao, Zhang Shuangle, et al.). 基于混沌二进制粒子群算法的独立微网系统的微电源组合优化 (Combinatorial optimization of micro-sources in standalone microgrid based on chaotic binary particle swarm optimization algorithm) [J]. 电力自动化设备 (Electric Power Automation Equipment), 2013,33(12): 33-38.

[19] 康守强, 王玉静, 杨广学. 等 (Kang Shouqiang, Wang Yujing, Yang Guangxue, et al.). 基于经验模态分解和超球多类支持向量机的滚动轴承故障诊断方法 (Rolling bearing fault diagnosis method using empirical mode decomposition and hypersphere multiclass support vector machine) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2011, 31(14): 96-102.

[20] 黄平 (Hang Ping). 粒子群算法改进及其在电力系统的应用 (Improved particle swarm algorithm and its application in power system) [D]. 广州: 华南理工大学 (Guangzhou: South China University of Technology), 2012.

Partial discharge pattern recognition based on autoregression model and hypersphere support vector machine

ZHANG Jian-wen1， WANG En-jun1， CHEN Huan-xu1，WANG Man1， DING Dong2

(1. School of Information and Electrical Engineering, China University of Mining and Technology,Xuzhou 221008, China; 2. Huangpu Wenchong Shipbuilding Company Limited,CSSC, Guangzhou 510715, China)

This paper proposes the partial discharge pattern recognition method which is based on autoregression model and hypersphere support vector machine in order to improve the accuracy of transformer partial discharge signals classification. The paper builds autoregression models for different types of discharge signals and makes the obtained model parameters as feature matrixes of partial discharge signals input into hypersphere support vector machine for the partial discharge signals classification. Since the penalty factor and the kernel function parameter play an important role on the classification accuracy for the hypersphere support vector machine, this paper makes use of the particle swarm algorithm to find the optimal combination of penalty factor and kernel parameter. The experimental results show that the classification accuracy of the optimized hypersphere support vector machine for partial discharge signals is 13.33% higher than that of the non-optimized hypersphere support vector machine and 20% higher than that of the BP neural network, which provides a new idea for the recognition of partial discharge signals.

partial discharge signal; autoregression model; hypersphere support vector machine; particle swarm optimization

2016-02-20

张建文(1968-)， 男， 宁夏籍， 教授， 博士， 研究方向为电气设备状态监测与故障诊断、 高电压与绝缘检测技术； 王恩俊(1990-)， 男， 山西籍， 硕士研究生， 研究方向为电气设备状态监测与故障诊断。

TM835.4

A

1003-3076(2016)09-0029-06