基于ANSYS的石油井架整体稳定性分析

盛　尹， 熊　峰， 葛　琪

(四川大学建筑与环境学院， 四川成都 610065)



基于ANSYS的石油井架整体稳定性分析

盛尹， 熊峰， 葛琪

(四川大学建筑与环境学院， 四川成都 610065)

【摘要】基于ANSYS对井架进行了线性屈曲分析和非线性屈曲分析，评估NDC-50DBT型石油钻机井架的整体稳定安全性能。论文提出屈曲控制荷载和非线性折减系数的概念，考虑几何和材料双重非线性，引入结构初始缺陷，采用弧长法进行非线性屈曲全过程跟踪。结果表明：对井架结构进行整体稳定分析时，有必要考虑风荷载的影响；相对于线性屈曲分析，非线性屈曲分析的屈曲因子为线性屈曲因子的0.33～0.72倍；考虑几何和材料双重非线性的多工况分析，能够更全面真实的反应井架稳定极限承载能力，为井架的设计和使用提供参考。

【关键词】井架；稳定性；非线性；有限元

石油钻机井架是钻机系统起升设备的重要组成部分，是用于放置天车和悬挂游车、大钩的专用工具，其性能直接关系到整套钻机系统的安全运行[1]。石油工程中使用的各种钻机井架大部分是由细长杆组成的杆系塔桅结构，使用中容易失稳。而钻井工程中发生的井架毁坏事故，往往是由于井架失稳造成的[2]。因此，对井架结构进行整体稳定性分析具有重要的实际意义。

本课题组基于ANSYS软件分析平台，对井架的整体稳定性进行评估，指导NDC-50DBT型石油钻机井架的设计和优化。为准确评价石油井架安全性能，本论文提出了井架屈曲控制荷载和非线性折减系数的概念，结合美国石油协会API规范和安装使用的实际，分析井架可能存在的危险工况，对各工况进行线性屈曲分析，得到结构线性屈曲因子。在此基础上，考虑结构初始缺陷，以线性屈曲模态修正有限元模型，考虑材料、几何双重非线性，对各工况进行非线性屈曲分析，求得非线性屈曲因子，全面评价井架力学性能，指导井架结构的优化改进。

1整体稳定性分析基本原理和方法

结构失稳是指结构在外力作用下平衡状态开始丧失，稍有扰动则变形迅速增大，最终遭到破坏的过程。对于石油钻机井架，就其性质而言，其失稳形式可分为线性屈曲和非线性屈曲[4]。

1.1线性屈曲分析原理

线性屈曲又称分支点失稳或第一类失稳。线性屈曲分析在数学上其可归结为广义特征值问题。对于线弹性构件，荷载-位移关系的矩阵形式为[5]：

(1)

式中：[P0]为施加荷载；[K]为刚度矩阵；[u0]为施加荷载[P0]的位移结果。

因此，增量的平衡方程为：

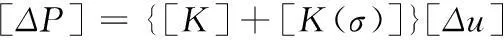
(2)

式中：[K(σ)]为应力状态[σ]下计算的刚度矩阵；[σ]为与[u0]对应的应力。

假设这是一个线弹性行为，则有：

得：

(3)

式中：μ为特征值。

当构件发生屈曲时 [ΔP]=0，则有：

(4)

由式(4)可以求得特征值μ，进而得到结构的临界屈曲荷载Pcr。

尽管线性屈曲只能用于预测理想线弹性结构的理论屈曲强度，对实际井架结构分析只能得到非保守结果，但是该方法计算速度快，有利于初步了解结构的稳定性，分析得到的临界荷载可作为后续非线性屈曲分析的目标荷载，屈曲模态也可作为非线性分析中引入初始缺陷的依据[6]，因此在进行整体非线性屈曲分析前，有必要对井架结构进行线性屈曲分析。

基于ANSYS的Eigen Buckling分析模块，可计算得到井架结构一系列的线性屈曲特征值。其中的最小值μ即为通常所称的线性屈曲因子或线性屈曲安全系数。结构的临界荷载为：

(5)

式中：Pcr为临界荷载；P为施加荷载。

然而，在安装使用过程中，并非所有荷载都对井架结构的屈曲起控制作用(如井架体自重)。把作用在井架上的荷载分为屈曲控制荷载和不变荷载，则式(5)可改写为：

(6)

式中:P1为控制荷载;P2为不变荷载。

由式(6)可以看出，将此处的μ作为井架结构的屈曲因子进行稳定性安全评价并不准确。

本课题组在对井架进行线性屈曲分析计算中，通过命令流不断调整式(6)中的控制荷载P1，使得到的结构最小特征值μ=1，此时式(6)可改写为：

(7)

(8)

将式(8)中的α作为井架的线性屈曲因子，这样能更准确反映井架的线性屈曲安全性能。PX称为施加的目标荷载。

1.2非线性屈曲分析原理

非线性屈曲又称极值点失稳或第二类失稳。非线性屈曲分析属于全过程大挠度弹塑性有限元方法，通过逐级增加荷载，不断修正单元的刚度矩阵，对结构进行非线性静力学分析，在此基础上寻找结构变得不稳定时的临界荷载。该方法能同时考虑结构的几何非线性、材料非线性以及结构初始缺陷。

借助ANSYS中的弧长法能实现石油井架非线性仿真分析。弧长法是一种稳定可靠的迭代控制方法，能有效的对平衡路径全过程跟踪。

在非线性屈曲分析时，本课题组结合改进的线性屈曲分析方法所得到的结果，采用多荷载步增量加载的方式，在0～10-6s时间步长内完成式(7)中不变荷载P2的等量逐步加载，接着在10-6～1 s内对目标荷载PX进行等量逐步加载，直到求解发散，非线性分析停止，得到分析停止时间T。

在分析计算中，ANSYS荷载步中的任意子步将被赋予合适的、线性插值得到的时间值，所以时间就可以作为荷载施加的跟踪参数[7]。井架结构的非线性屈曲因子(非线性屈曲安全系数)按式(9)计算。

(9)

式中：n为非线性屈曲因子；α为相应工况线性屈曲因子；T为ANSYS非线性分析终止时间，可视为非线性折减系数。

该分析过程中考虑结构的几何非线性和材料非线性，同时参考文献[6]中对空间钢结构的分析方法，以结构一阶线性屈曲模态位移值的0.1倍修改原模型节点坐标，作为结构的初始缺陷。

2荷载与工况分析

2.1井架的计算荷载

作用在井架上的荷载可分为恒定荷载、工作荷载和自然荷载，在进行井架结构整体稳定性分析时，考虑如下荷载：

(1)恒载。包括井架体本身的重量以及安放在井架上面的各种附件设备(主要包括井架自重、二层台重量、天车重量、游动系统等)的重量。

(2)最大钩载。即钻机最大起重量,是钻机的一个主参数。

(3)工作绳作用力。在给定的游动系统下，快绳和死绳拉力的垂直分力。

(4)立根荷载。在钻井过程中靠放在钻台上的立根对井架产生的作用力，通过二层台指梁按水平方向作用到井架。

(5)风载。井架结构在环境风作用下所受到的荷载，包括井架体风载和立根风载。

2.2荷载工况

结合API规范和实际安装使用情况，考虑井架生命周期可能出现的平躺、起升、竖直状态，整体稳定性计算工况见表1。

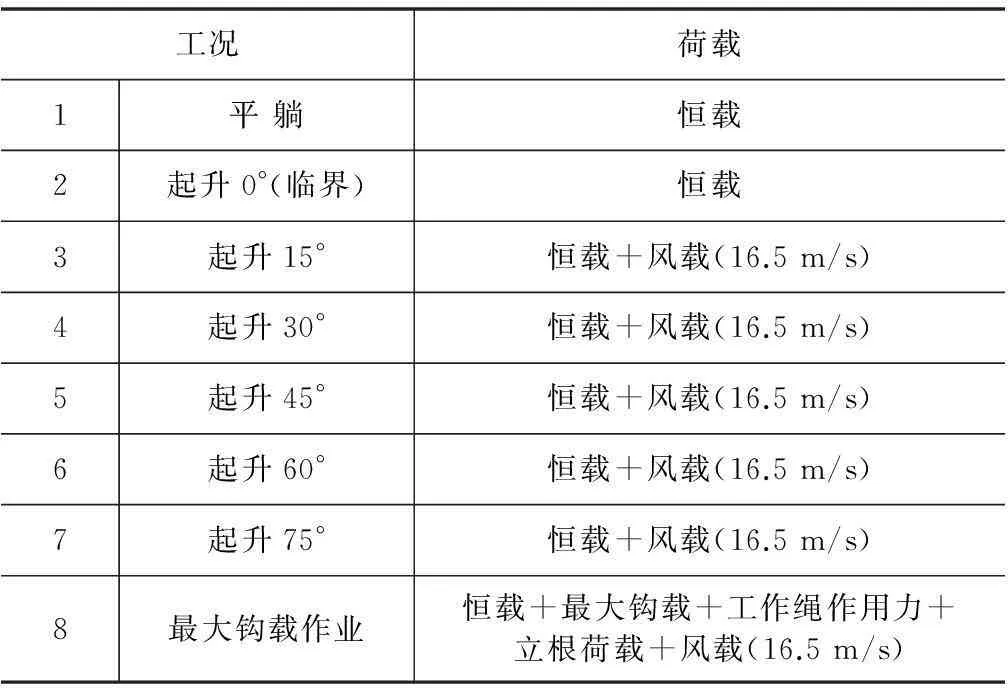
表1　荷载工况

注：①对于计入风载的工况，分别考虑X、Y风向；

②井架安装作业设计抗风能力为16.5 m/s。

3有限元分析模型

3.1模型建立

该井架为前开口型结构，属6×7轮系，最大设计钩载4 500 kN，由上、中、下段组成。在ANSYS中建立模型时，作如下假设简化：井架杆件间连接可靠，为刚性连接；忽略二层台、天车、工作梯及护栏等对井架的刚度影响，只计入其自重荷载。分别建立各状态结构模型，其中井架竖直状态模型如图1所示。

图1　结构模型(竖直状态)

结构构件采用Q345和Q420钢材，材料参数如表2所示。考虑材料非线性时，选用双线性等向强化模型，即材料应力-应变曲线由两段直线组成，包括弹性和塑性两个斜率。弹性段斜率为弹性模量E，塑性段斜率ET取值为0.1E。

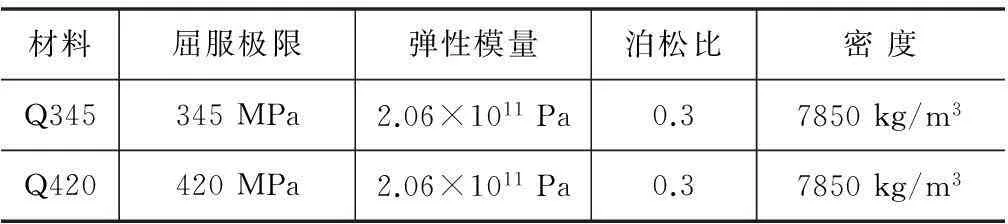
表2　材料参数

选用BEAM189单元进行模拟分析。BEAM189是3D二次有限应变梁单元，非常适用于线性、大角度转动和非线性大应变问题。设置单元属性 KEYOPT(1)=1，添加单元第7个自由度(横截面的翘曲)。综合考虑分析精度和时间内存消耗，模型单元长度设为0.2 m，共4 080个单元，11 396个节点。

3.2荷载施加

对表1中各工况按以下方式分别施加荷载：

(1)井架体自重以惯性力的方式施加。

(2)二层台相关附件重量均分到二层台架体各节点上。

(3)游车、钻井绳及其他附件的重量均分到井架顶端4个节点上。

(4)钩载、工作绳作用力均分到井架顶端4个节点上。

(5)立根水平靠力均分到二层台指梁相应节点上。

(6)风载分配到井架体迎风面节点上。

4结果与分析

4.1线性屈曲

以最大钩载y风向工况为例，选取最大钩载(P1=4 500 kN)作为结构屈曲控制荷载，其余荷载为不变荷载。当施加荷载为(6×控制荷载+不变荷载)时，结构最小特征值为1.003，接近1.0，根据式(7)、式(8)可得结构该工况线性屈曲因子α=6。结构一阶屈曲模态如图2所示。

图2　一阶屈曲模态(放大5 000倍)

同理，对其余工况进行分析，各工况控制荷载P1和线性屈曲因子α如表3所示(括号内为y风向时的结果)。

由表3可得：

(1)各工况线性屈曲因子并不相同，同种工况不同方向风荷载下屈曲因子也不完全相同，因此有必要对井架的安装起升状态进行分析，并考虑风荷载的影响。

(2)井架在各工况中最小线性屈曲因子αmin=6，可初步判定井架整体稳定性良好。

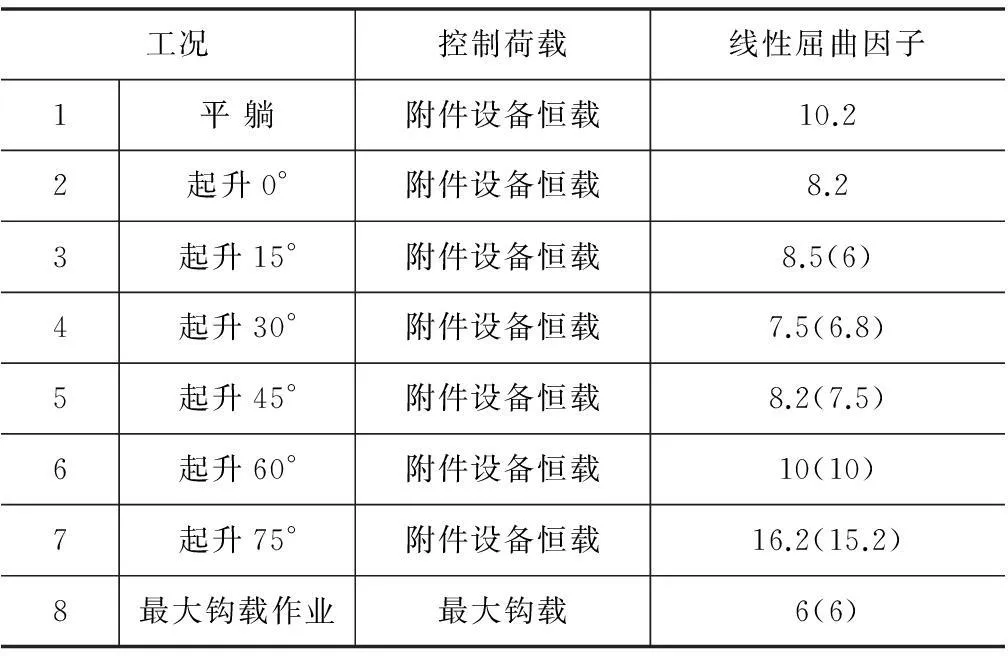
表3　各工况线性屈曲因子

注：附件设备恒载指井架结构除井架体自重外的其他所有恒载。

4.2非线性屈曲

以最大钩载y风向工况为例，根据线性屈曲分析结果，对结构依次等量逐级施加不变荷载P2和目标荷载PX=(6×P1),得到结构非线性折减系数(分析终止时间)T=0.37，由式(9)可得井架非线性屈曲因子n=6×0.37=2.22。

图3为该工况井架顶部节点竖向位移与荷载关系曲线。A点表示结构仅在不变荷载P2作用下顶点竖向位移值。经分析发现，当目标荷载PX达到7 110 kN(1.58倍控制荷载)附近时，井架部分构件开始进入屈服，如图中B点所示。当目标荷载PX达到9 990 kN(2.22倍控制荷载)后，位移值迅速增加，且荷载有减小的趋势，整体结构达到承载极限状态，如图中CD段所示。图中AB段实线与虚线的偏离表明整体结构在材料屈服前因几何非线性效应已表现出明显的非线性现象。

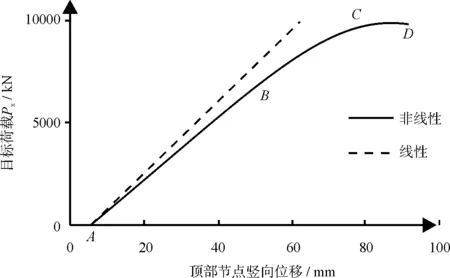
图3　荷载位移曲线

同理，对其余荷载工况进行非线性屈曲分析，各工况非线性折减系数T及屈曲因子n如表4所示(括号内表示y风向时的结果)。

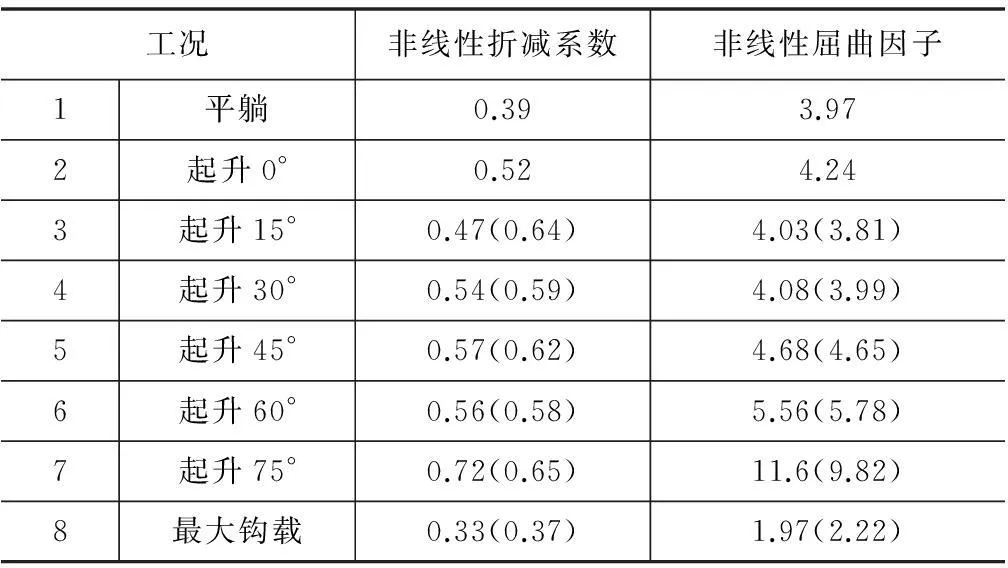
表4　各工况非线性屈曲因子

从表4可以看出：

(1)各工况非线性屈曲因子均明显小于表3中的线性屈曲因子，其值约为线性屈曲因子的0.33～0.72倍。

(2)同种工况不同风向分析结果并不相同，表明在在非线性分析中，风荷载的影响并不能忽略。

(3)井架最小非线性屈曲因子nmin出现在最大钩载x风向工况，大小为1.97。

5结论

通过计算分析可得出以下结论:

(1)线性分析方法会过高地估计结构的极限承载力，要准确评估出作业井架的极限承载力必须同时考虑几何和材料非线性。

(2)相比于线性屈曲因子，非线性屈曲因子折减系数为0.33～0.72。

(3)对井架结构稳定性的安全评估，应考虑风载的作用。

(4)通常情况下，当结构的屈曲因子大于1时，可认为结构是稳定的。文献[2]和文献[8]中提到，井架结构的整体稳定性许用安全系数为2.2，即当屈曲因子大于2.2时井架具有足够的整体稳定性安全裕度和良好的抗失稳性能。在所有工况非线性分析结果中，平躺起升过程的非线性屈曲因子均大于2.2，表明这些工况下结构稳定性是足够安全的；对于最大钩载的极限状况，y方向风荷载时，非线性屈曲因子为2.22，能够满足稳定需求；对于最大钩载x风向时，结构非线性屈曲因子为1.97，大于1，但小于文献中的2.2，即在该极限工况下，其整体稳定性并不能得到足够的保证，应对该结构构件的截面尺寸进行改进设计。

(5)考虑几何和材料双重非线性的多工况分析，能够更全面真实的反应井架稳定极限承载能力，为井架的设计和使用提供参考。

参考文献

[1]熊敏.考虑半刚性节点的塔形井架结构有限元分析[D].大庆:东北石油大学,2013.

[2]张学鸿,刘巨保,王惠德.3 200 m钻机前开口井架整体稳定性分析[J].石油机械,1990,18(5):1-3.

[3]周传喜,郭伟,南利华.海洋修井机井架稳定性计算研究[J].石油机械,2009,37(8):48-50.

[4]张嗣伟.井架总体稳定性的概念与计算原理[J].石油机械, 1978(4):117-132.

[5]高超,郭建生.圆管钢结构稳定性的有限元分析[J].武汉理工大学学报:信息与管理工程版, 2011,33(3):421-423.

[6]陈志华,刘红波,周婷,等.空间钢结钩APDL参数化计算与分析[M].北京: 中国水利水电出版社,2009.

[7]李兵,宫鹏涵.ANSYS14有限元分析自学手册[M].北京:人民邮电出版社,2013.

[8]蒋薇,易先中,胡德祥.JJ225/42-KC型石油钻机井架结构强度分析[J].石油机械, 2012,40(2):22-25.

【文献标志码】A

【中图分类号】TE923; TU311.2

[通讯作者]熊峰(1963～)，女，教授，博士生导师。

[作者简介]盛尹(1992～)，男，在读研究生，研究方向：工程结构分析。

[收稿日期]2015-10-22