预压型钢混凝土柱轴压比推导及轴压比限值分析

张　涛, 张　波

(1. 通用地产长沙有限公司, 湖南长沙 410076; 2. 铁四院(湖北)工程咨询有限公司, 湖北武汉 430000)



预压型钢混凝土柱轴压比推导及轴压比限值分析

张涛1, 张波2

(1. 通用地产长沙有限公司, 湖南长沙 410076; 2. 铁四院(湖北)工程咨询有限公司, 湖北武汉 430000)

【摘要】文章对预压型钢混凝土柱轴压比公式进行了推导，引入了参数预压比并分析了其对轴压比的影响，通过算例对预压型钢混凝土柱轴压比限值进行了分析，并提出了预压型钢混凝土柱轴压比限值，对于工程应用计算有一定的实际意义。

【关键词】预压型钢混凝土柱；预压比；轴压比

近年来，型钢混凝土结构及其结构性能和施工工艺上的众多优点在国内外高层建筑中悄然兴起，成为了高层建筑结构体系中的重要形式。预压型钢混凝土柱是通过施工工艺的改变，将一期轴力单独施加到型钢上，剩余轴力由混凝土和型钢分担，降低了混凝土部分的轴压比。这样就给预压型钢混凝土柱提供了更大的轴压比限值空间,可以提高柱的轴压比限值，充分发挥型钢的作用。

在结构设计中，柱轴压比的取值不仅对结构的抗震性能有很大的影响，同时也是确定柱子的截面尺寸、型钢含量及抗震配筋构造等的重要依据。然而，业内对型钢混凝土柱轴压比的定义有很大分歧，而对其限值则更是没有统一的看法，我国现行的两部SRC结构的行业标准，其适用范围均明确规定为适用于实腹式配钢的SRC柱,而对于预压型钢混凝土柱的轴压比限制的研究尚属少见,很少有相关的参考文献。本文主要是通过对预压型钢混凝土柱轴压比公式进行推导，引入参数预压比并分析其对轴压比的影响，提出了预压型钢混凝土柱轴压比限值，从而为预压型钢混凝土柱结构的推广应用提供理论基础和技术支持。

1型钢混凝土柱轴压比

我国学者叶列平教授首先提出对于型钢混凝土柱应采用轴压力限值系数[1]，不应继续沿用钢筋混凝土柱轴压比限值。因为对于型钢混凝土柱主要配置了型钢，在轴向压力作用下型钢承担了很大一部分轴力，且型钢含量直接影响到型钢混凝土柱承受轴压力的大小和抗震性能，而钢筋混凝土轴压比公式中不含型钢项，因此采用钢筋混凝土柱轴压比公式不妥。型钢混凝土柱轴压比限值推导如下。

对于钢筋混凝土柱，轴压比公式为：

(1)

式(1)可变形为：

N=nfcA

(2)

如果取上式n为轴压比限值，则上式确定的轴压力称为轴压力限值，对于型钢混凝土柱，其轴压力由混凝土和型钢两部分共同承担，可以表示为：

N=ncfcAc+nsfsAs

(3)

其中：nc为混凝土轴力分配系数；ns为型钢轴力分配系数。在设计状态下nc和ns基本相同，为便于计算，将式(3)变形为：

N=n(fcAc+fsAs)

(4)

式中：N为型钢混凝土柱的轴压力限值；n为型钢混凝土柱的轴压力限值系数。

我国《型钢混凝土组合结构技术规程》[2]中定义型钢混凝土柱的轴压比公式为：

(5)

式中：N为轴向压力设计值；fc为混凝土轴心抗压强度设计值；fs为型钢抗压强度设计值；Ac为柱截面中混凝土的面积；As为型钢的截面积。

2预压型钢混凝土柱轴压比公式推导[3-4]

与钢筋混凝土柱相同，预压型钢混凝土柱也以受压区边缘高强混凝土达到极限压应变εcu=0.003，且最外侧受拉纵筋同时达到屈服作为预压型钢混凝土柱大小偏心破坏的界限状态，并由此确定预压型钢混凝土的轴压比限值(图1)。

图1　预压型钢混凝土柱截面

预压型钢混凝土柱在一期和二期轴力作用下的压应变分布及界限状态时截面的应变分布如图2。

图2　截面极限状态的应变分布

图中εso为第一期轴力在钢骨上产生的压应变，假设钢骨与混凝土之间无滑移，则在界限状态时同一位置处钢骨和混凝土之间的应变差仍为εso；ε2为第二期轴力在整个预压型钢混凝土柱截面上产生的压应变；εcu为混凝土的极限压应变，通常取为0.003；εy为最外排受拉纵筋的屈服应变，εy=fy/Es，其中fy是钢筋的屈服强度，Es为钢材的弹性模量；εsy为钢骨的屈服应变，εsy=fs/Es，其中fs是钢骨的屈服强度；εsa为位于混凝土受压区的钢骨翼缘处的压应变；εsb为位于混凝土受拉一侧的钢骨翼缘压应变，可能受压可能受拉；h、h0分别为截面的高度和有效高度，h0=h-as，as为受拉钢筋合力作用点至截面受拉边缘的距离；b为截面的宽度；hw为钢骨腹板的高度；ha、hb分别为钢骨翼缘重心距截面受压、受拉边缘的距离；x0为混凝土实际受压，区的高度；hc为钢骨腹板上应变恰好达到屈服应变εsy的点距截面受压边缘的距离；hd为钢骨腹板上应变为零的点距截面受压边缘的距离。

根据图2所示界限状态时的应变分布，并假定压应变为正，拉应变为负，可分别求出上述参数的表达式，即:

(6)

(7)

hc点处的压应变恰好达到钢骨的屈服应变εsy，所以有:

(8)

(9)

hd点处的压应变为0，所以有:

(10)

(11)

这里需要说明的是:在预压型钢混凝土柱中,钢骨可能全截面受压，钢骨腹板中并不存在压应变等于零的点，这时hd=ha+hw。

另外，由于钢骨截面的高度一般不应小于柱截面总高度的60 %，所以可取ha=hb=0.2h0。

(12)

预压型钢混凝土柱截面处于界限状态时，混凝土承担的轴力为:

(13)

式中：Ac是混凝土的截面面积；α1为混凝土强度系数；ξb为混凝土界限相对受压区高度。

下面给出界限状态时钢骨承担的轴力。钢骨腹板的应力分布(假设翼缘厚度远小于腹板高度)可能有两种情况：

(1)腹板部分截面受拉。此时受拉腹板中高度为c部分的合拉力与反对称的受压腹板的相应部分的合压力抵消，因此合力由腹板受压区中剩下的两部分压力组成，即高度a的受压屈服区部分的压力和高度为d的没有屈服的部分的压力(图3)。

图3　钢骨腹板应力(a)

对于第一种情况有：

2hd+hb-h-hc

(2)腹板全截面受压。整个腹板只存在高度为a的受压屈服区和高度为d的未屈服区两部分(图4)。其中特征参数a为a=hc-ha。

图4　钢骨腹板应力(b)

对于第二种情况，d可以表示为：

d=hw+ha-hc

则钢骨翼缘和腹板的轴力分别为：

(14)

(15)

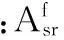
(16)

(17)

在此引入参数η，η=εso/εsy为与预压比m相关的系数，表示第一期轴力与钢骨屈服轴力之比。

(18)

(19)

式中ηb为轴压比限值标准值。

3算例

(第一种情况)

(第二种情况)

(第一种情况)

(第二种情况)

由εsb=(η-1)εsy可以看出，当η≥1时，εsb>0，εsa>0，则钢骨全截面受压，不存在应变为零的点；当η=0(不预压)时，εsa=1.2εsy，说明即使不预压，钢骨受压翼缘也能达到屈服强度。当将上述各项分别对应代入式(16)和式(17)，可得：

(第一种情况)

(第二情况)

综合以上各式，取不同的η值，可以求得预压型钢混凝土柱的Nb,进一步计算轴压比限值nb和对应的预压比m，计算结果见表1。

表1　预压型钢混凝土柱的轴压比限值(标准值)

由此可见，在其它参数相同的情况下，随着预压比的增大，预压型钢混凝土柱的轴压比限值增大。说明采用预压型钢混凝土柱，即使在较大轴力下，预压型钢混凝土柱也会发生大偏心延性破坏。

4结论

(1)轴压比是影响预压钢筋混凝土柱延性的重要因素，轴压比越大则延性越差。

(2)本文计算了一预压型钢混凝土柱随预压比m变化的轴压比限值nb。通过算例分析可知，随着预压比m的增大，预压型钢混凝土柱的轴压比限值也增大，说明了采用预压型钢混凝土柱，可以有效提高柱体的抗震性能。

参考文献

[1]叶列平.钢骨混凝土柱的设计方法[J].建筑结构，1997(5)：8-12.

[2]叶列平，方颚华，周正海，等.钢骨混凝土柱的轴压力限值[J].建筑结构学报，1997,18(5)：40-50.

[3]JGJ 138-2001 型钢混凝土组合结构技术规程 [S].

[4]张涛.低周期反复荷载下预压型钢混凝土柱数值模拟和非线性分析[D].长沙：长沙理工大学,2009.

【文献标志码】A

【中图分类号】TU312

[作者简介]张涛(1983～)，男，研究生，一级注册结构工程师，从事结构设计工作；张波(1981～)，男，本科，国家注册监理工程师，从事工程监理工作。

[定稿日期]2015-09-07