导数应用中“数形结合”的辅助功能



导数应用中“数形结合”的辅助功能

◇甘肃何军海

导数背景下的函数问题,一直是高考数学命题的热点,本文结合自己的教学实际,通过具体例析,谈一谈导数背景下运用数形结合思想的解题策略,以期抛砖引玉．

1函数类不等式的证明问题

f′(x)=1/x+lnx=1/x-ln(1/x).

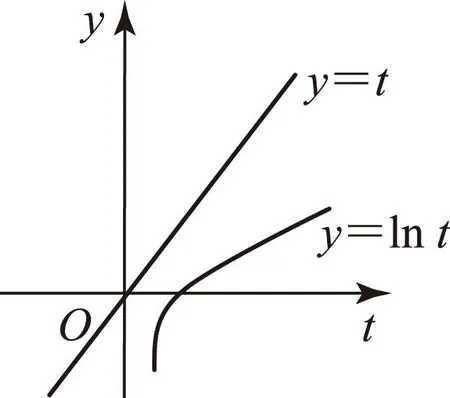
图1

为研究方便,设1/x=t,则h(t)=t-lnt.画出函数y=t和y=lnt的图象(如图1),可以看出函数y=t的图象永远在y=lnt的图象上方,故h(t)=t-lnt>0,因此f′(x)≥0恒成立,说明f(x)=(x+1)lnx-x+1在其定义域上是增函数.

可知,若x-1≥0,x≥1,则f(x)≥f(1)=0;若x-1<0,x<1,则f(x)

综上所述,(x-1)f(x)≥0.

2函数零点个数的判断问题

图2

3函数方程中参数范围的确定问题

图3

(作者单位：甘肃省嘉峪关市第一中学)