小子样定数试验方案设计研究

张志辉

(解放军91404部队，秦皇岛 066001)



小子样定数试验方案设计研究

张志辉

(解放军91404部队，秦皇岛 066001)

摘要：为了使研制方和使用方承担的试验风险计算更为准确、明确，对风险计算方法进行了改进，对定数试验方案设计采用的风险相当原则合理性进行了研究，提出了军用装备验证试验的方案设计原则。

关键词：试验风险；小子样；试验设计

0引言

在当前试验中，由于被试品科技含量的增加，研制生产成本不断攀升，消耗型被试品的试验成本也随之不断增加，对消耗型被试品进行大样本试验已经不可能。如何采用小样本，且科学合理地对成功率、可靠性等概率性指标进行考核将是试验中经常面临的主要问题。本文从风险计算出发，对小样本定数试验方案设计进行研究。

目前，试验风险计算多采用二项分布经典假设检验方法。为方便风险计算方法描述，假设干扰成功率为p，总试验次数为k，可接受成功次数为n，干扰成功率指标为p0。

1二项分布经典假设检验方法计算试验风险

鉴别比定义为：

(1)

式中：p1为不可接收的成功概率。

采用假设检验的方法做如下假设[1]:

(2)

式中：H0为原假设；H1为对立假设。

风险计算[2]：

该方法是没有计算机辅助计算时多采用的一种近似计算方法。事实上，成功率p可能是区间[0,1]内的任一值，但采用此方法做了一个非此即彼的假设，即成功率p被假设为不是p0就是p1，该假设引入了较大误差。同时引入了不确定参数鉴别比，该参数对风险有较大影响。

2风险计算改进方法

为了避免经典假设检验引入的假设误差，针对假设问题进行改进。把公式(2)修改为：

(3)

若存在可使用的先验信息，在计算风险前，应当根据先验信息计算干扰成功率分布；若无任何先验信息或先验信息描述不清楚时，可认为干扰成功率在[0,1]区间均匀分布。

计算时，采用数值法进行计算，干扰成功率在[0,1]区间等间隔取M个点，各点出现概率相同。则：

(4)

同理：

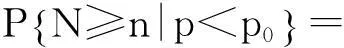
(5)

采用数值法计算同样引入了量化误差，但随着M值的变大，量化误差越来越小，当M值较大时，误差可以忽略。计算时，M一般取10 000，可采用计算机辅助计算，计算量并不大。

以干扰成功率指标P0=0.8、试验次数k=10为例，采用2种方法计算风险的结果如表1所示。

从表1中可以看出，采用二项分布经典假设检验计算方法，不同的鉴别比其研制方风险相同，但使用方风险结果多了1个鉴别比参数。不同的鉴别比，使用方风险相差较大，鉴别比越高，使用方风险越小。这样试验考核采用不同的鉴别比，考核难易程度相差较大，鉴别比值的商定容易成为争执焦点。

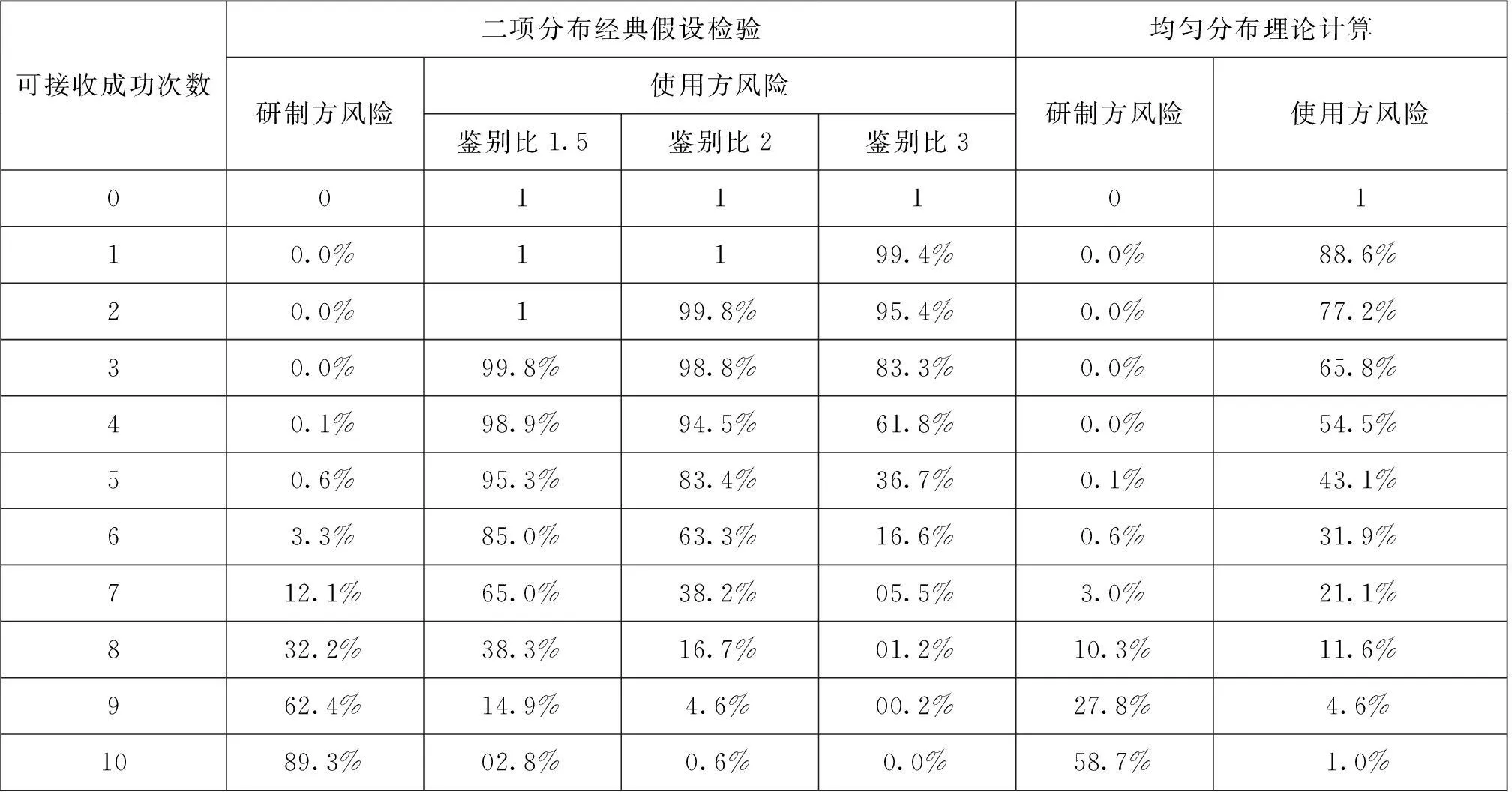
表1　风险计算对照表

从表1中可以看出，与二项分布经典假设检验计算方法相比，风险计算改进方法计算的研制方风险更小，且使用方风险是固定明确的。

综上所述，风险计算改进方法更为合理。

3定数试验方案设计

成功率、可靠性等概率性指标考核，若指标要求规定了置信度，可以根据置信度确定试验样本，相关军标有具体可行方法，本文不再赘述。若指标要求未规定置信度，试验方案设计应当以研制方和使用方承担试验风险为依据。

目前，民品验证性试验多采用风险相当原则，即研制方和使用方选择试验承担的风险相当，可根据双方承担的风险确定样本量。对于民品的研制方和使用方，承担风险的后果相同，风险相当原则较为合理，如GB5080.5-1985 《设备可靠性试验成功率的验证试验方案》等采用了此原则。但军品验证试验过程中，研制方和使用方承担风险后果是有较大区别的，研制方风险仅关系弹药的消耗数量问题，即经济问题；而使用方风险关系战士性命、战争成败，甚至关系国家命运，因此，在军品验证试验时，采用风险相当原则是不合理的。

在军用装备验证试验时，使用方风险应当根据装备的使命任务、价格等综合考虑，这些考虑因素在装配的数量中均有体现，因此应当根据预计装配数量分档选择使用方风险。装配数量越大，选择越小的使用方风险值，建议分档选择对应关系见表2。

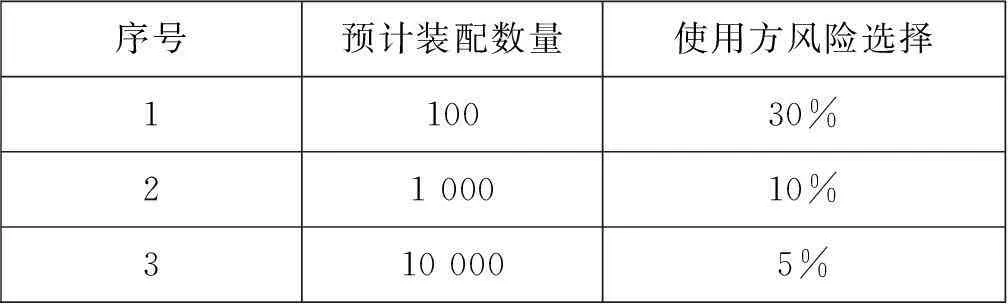
表2　使用方风险选择表

当预计装配数量小于100时，一般为特殊装备，如核弹、火箭等，可发射1枚进行验证；当预计装配数量大于10 000时，应当进行大样本试验，不考虑风险问题；当预计装配数量不是很明确的情况下，一般选择10%。

而研制方风险由研制单位自己选择确定，试验样本数可根据双方确定的风险计算获得。同时，当使用方风险确定后，最小样本量就已经确定。

定数试验方案设计实例：某型弹成功率指标要求为0.6，预计装配数量为1 000枚，使用方风险选择0.1。满足条件的试验样本和试验成功次数见表3。

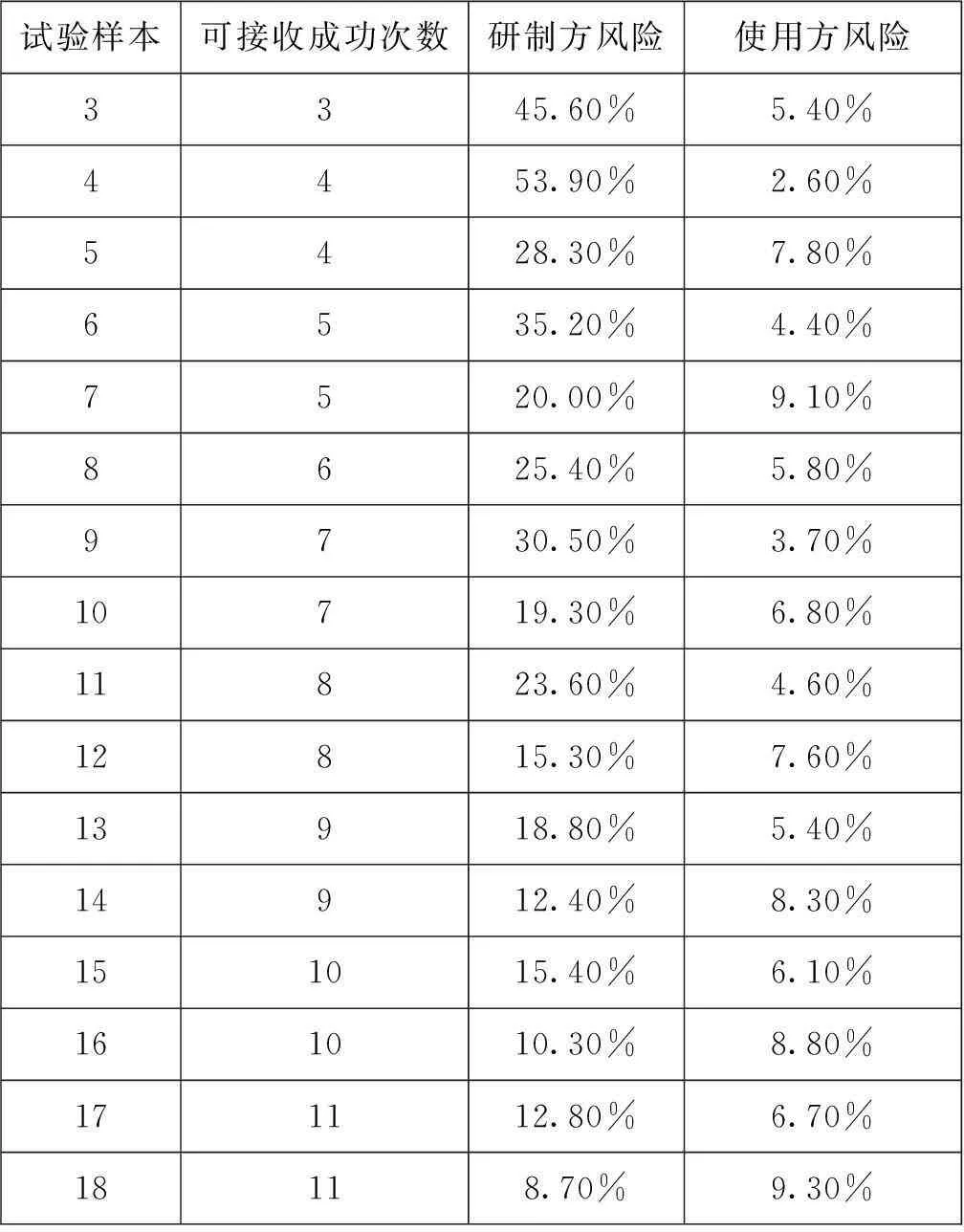
表3　试验样本及试验可接收成功次数

从表3可以看出，研制方根据自身能够承担的样本量选择研制方风险。

研制方选择风险低于30%时，试验选择样本数5，试验可接受成功次数为4。

研制方选择风险低于20%时，试验选择样本数7，试验可接受成功次数为5。

研制方选择风险低于10%时，试验选择样本数18，试验可接受成功次数为11。

研制方选择最小样本数3时，试验选择样本数3，试验可接受成功次数为3。

4结束语

本文对风险计算方法进行了改进，使得计算的研制方和使用方承担的试验风险更为准确、明确，同时对定数试验方案设计采用的风险相当原则合理性进行了研究，根据预计装配数量不同，提出了军用装备验证试验的方案设计原则。

试验设计时，应当仅考虑使用方风险，不考虑研制方风险。当预计装备数量小于100时，可发射1枚进行验证；当预计装配数量大于100时，使用方风险选择10%进行试验设计；当预计装备数量大于1 000时，使用方风险选择5%进行试验设计；当预计装配数量大于10 000时，应当进行大样本试验；当预计装配数量不明确时，一般使用方风险选择10%进行试验设计。

参考文献

[1]姜礼平，吴晓平，戴明强.工程数学[M].武汉：湖北科学技术出版社，2008:374-375.

[2]曲宝忠，孙晓峰.海军战术导弹试验与鉴定[M].北京：国防工业出版社，2005:64-65.

Research into Design Scheme of Small Sample Fixed Number Test

ZHANG Zhi-hui

(Unit 91404 of PLA,Qinhuangdao 066001,China)

Abstract:In order to make the test risk calculation of developer and user more accurately and definitely,the risk calculating method is improved,the rationality of risk correspondence fundamental adopted by fixed number test scheme is studied,the design fundamental of military equipment validation test scheme is put forward in this paper.

Key words:test risk；small sample；test design

DOI:10.16426/j.cnki.jcdzdk.2016.01.019

中图分类号：TJ76

文献标识码：A

文章编号：CN32-1413(2016)01-0089-03

收稿日期:2015-11-26