基于改进型最大信噪比算法的抗压制性干扰研究
2016-04-28王雨
王 雨
(西安电子科技大学,西安 710071)
基于改进型最大信噪比算法的抗压制性干扰研究
王雨
(西安电子科技大学,西安 710071)
摘要:自雷达诞生以来,抗干扰能力一直是评价一部雷达性能的关键性指标,特别是随着战场电磁环境的日益复杂,雷达抗干扰问题变得尤其重要。针对抗压制性干扰,改进了传统意义上基于最大信噪比的盲源分离算法,提出了使用干扰重构算法取代滑动平均处理的方法,获得了比传统方法分离出质量更高的雷达信号,输出信号与源信号相关性更强。
关键词:抗压制性干扰;盲源分离;最大信噪比;干扰重构
0引言
现代战争中,雷达电子对抗的作用日益凸显,雷达抗干扰性能成为衡量一部雷达优劣的重要指标。战场上电磁环境极其复杂,敌方蓄意干扰、友方同频波段、各种工业波段、自然环境中的各种杂波等充斥整个空间,所以研究雷达抗干扰技术是十分有意义的。目前在有源干扰方面,雷达干扰机主要使用压制性干扰和欺骗性干扰两大类,其中压制性干扰主要通过发射大功率的噪声信号来掩盖或吞没敌方雷达荧光屏上的目标回波信号,使敌方雷达无法正常工作[1];压制性干扰主要以噪声调频干扰为主,所以本文主要研究了基于信噪比最大化的盲源分离技术抑制噪声调频压制性干扰的问题。
盲源分离技术是指在源信号和传输通道参数未知的情况下,根据输入信源信号的统计特性,仅由观测信号检测并分离出信源信号中各个独立成分的过程,这一过程又称为独立元分析(ICA)[2]。近年来盲源分离在语音、通信、生物电等信号处理领域的应用日益广泛。它起源于对神经网络的研究,在1985~1989年,法国学者Jutten和Herault考虑了2个源信号的瞬时混叠和分离问题,提出了简单的高阶去相关神经网络方法[3];1994年P.Comon提出了ICA的概念,并给出了相关信息论准则[4];张贤达教授等人提出了一种新的信号盲分离算法,可以系统化地得到全部独立分量[5]。以上算法都是基于自学习循环迭代得到某种目标函数最优化的算法,2001年J V Stone提出了基于时频预测的盲源分离算法,为最大信噪比盲源算法提供理论基础。该种算法在预测源信号的过程中形成了广义特征值问题[6],该问题的特征向量就是混合矩阵的分离矩阵近似,因此该算法具有低复杂度,不需要迭代运算。但文献[7]简单地使用滑动平均算法对源信号进行预测,预测度并不高。本文提出了使用干扰重构算法代替滑动平均,取得了对源信号较好的估计,将此估计作为最大信噪比盲源分离算法中的信号预测,最终分离出较好的源信号。
本文首先对雷达使用的信号模型和干扰模型进行了研究;然后描述盲源分离的数学原理,对混合信号进行去中心化和白化预处理后,采用干扰重构算法得到源信号的预测,采用预测信号与预测信号和源信号之间的误差之比作为信号最优化的判别,求出分离矩阵,再处理分离后的信号得到目标物距离。
1信号模型
1.1雷达发射信号模型
雷达使用的发射信号种类繁多,单从信号的频域波形方面考虑就有:跳频信号、频率分集信号、宽瞬时带宽信号、脉冲压缩信号、频率捷变信号、波形捷变信号、相位编码信号等。本文采用的源信号为典型的线性调频信号,其数学表达式为:
(1)
式中:τ为脉宽;f0为中心频率;μ为调频斜率。
假设目标为静止的,因此雷达回波信号仅仅包含时移τ0=2R/c,即s0(t-τ0),其中R为目标物距离雷达的径向距离,c为光速。
1.2压制性干扰模型
压制性干扰主要分为:噪声调频干扰、射频噪声干扰、噪声调幅干扰以及噪声调相干扰等,其中噪声调频干扰使用最为广泛,所以本文中使用的干扰模型将采用噪声调频干扰,其数学表达式为:
(2)
式中:调制噪声u(t)为零均值的广义平稳随机过程;φ为[0,2π]均匀分布的随机变量,且与u(t)相互独立;噪声调频干扰的振幅Uj、中心频率wj和调频斜率KFM都为常数。
2干扰重构算法
在文献[8]中介绍了一种干扰重构的算法,基本原理就是从回波中得到干扰参数,重构干扰信号,从雷达接收信号中消去重构的干扰信号,达到抑制干扰的作用。这里假设雷达接收信号模型为:
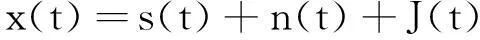
(3)
(4)
式中:s(t)为目标回波信号;n(t)为等效噪声信号;J(t)为噪声调频干扰信号。
因为当干扰功率比较大时等效噪声的干扰效果就会减弱,所以高干信比条件下,可以将等效噪声与目标回波和记为:
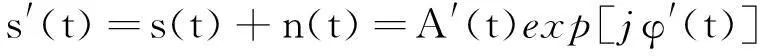
(5)
此时:
(6)
利用噪声调频干扰的恒模特性,可以将上式写为:
(7)
(8)
由上式可得:
(9)
对式子两边同时进行对数运算,并进行一阶泰勒展开得:
ln[x(t)]=ln[J(t)]+ln[1+s1(t)]≈
ln(Aj)+j[φj(t)-2kπ]+s1(t)
(10)
分别取它的实部和虚部,记为Rx(t)和Ix(t),则有:
(11)
(12)
利用目标回波信号和噪声调频干扰信号是零均值的特性,可以估计干扰信号的幅度:
(13)
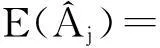
exp{E{mean{lnAj+Re[s1(t)]}}}=
exp{lnAj+E{mean{Re[s1(t)]}}}=Aj
(14)
进而可以得到:
(15)
在|s1(t)|≪1的条件下,干扰信号的估计为:
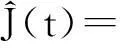
(16)
从接收信号x(t)中消去干扰信号的估计值可以得到目标回波信号的估计:
(17)
这样就可以得到雷达目标回波信号,该算法的缺点是对干信比比较敏感,即大功率干扰下目标回波估计较差,因此单独作为干扰抑制算法效果很差,但作为从雷达接收信号中估测源信号,不仅估测精度比滑动平均处理好而且运算量小,之后通过最大信噪比盲源分离算法处理后,使得分离效果更好。下面介绍最大信噪比盲源分离算法模型。
3改进型最大信噪比的盲源分离抑制干扰算法
盲源分离是在对原始信号的特征了解甚少,甚至不知道混合信号中源信号数目的情况下,从混合信号中分离出原始信号[9]。由于只能得到雷达天线的接收信号以及发射信号副本,且接收信号中包含了大量的干扰成分,所以可以假设如下信号模型:
(18)
式中:x(t)为雷达观测信号矩阵,x(t)=[x1,x2,…,xn]T;s0(t)为纯净的雷达回波信号和单纯的干扰信号构成的矩阵;A为干扰强度、雷达天线、系统噪声等因素决定的混合矩阵。
假设分离矩阵为W,则对源信号的估计信号y(t)为:
y(t)=Wx(t)=WAs0(t)
(19)
在此信号模型中,将抽取源信号和其估计信号的误差:e=s0-y,只要使该误差最小化,则可以将信号y(t)作为源信号s0(t)的估计,进而分离出雷达回波信号,抑制干扰。文献[7]给出了信噪比函数作为误差最小化的计算公式:
(20)
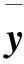
(21)
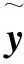
(22)
以F(y)作为目标函数进行自学习,使得输出信号与源信号的误差最小,得到较好的源信号估计。进一步可对目标函数进行如下运算:
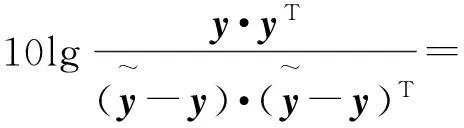
(23)
进而求其关于分离矩阵W的梯度:
(24)
因为在最大信噪比的极值点处该梯度值等于0,于是可以得到:
(25)
4仿真实验与结果分析
为了验证上述理论,设定如下仿真参数:雷达发射信号的脉冲周期T=40 μs,信号带宽B=30 MHz,信号采样率Fs=100 MHz,接收窗口[10 000,15 000]m,目标物与雷达径向距离R=12 000 m。干扰信号为噪声调频信号,调频斜率Kfm=1 000,中心频率f0=15 MHz,干扰带宽=20 MHz,采样点数为4 000,信噪比=10 dB,干信比=30 dB;干扰信号时频图如图1所示,雷达接收机接收到的两路信号如图2所示。
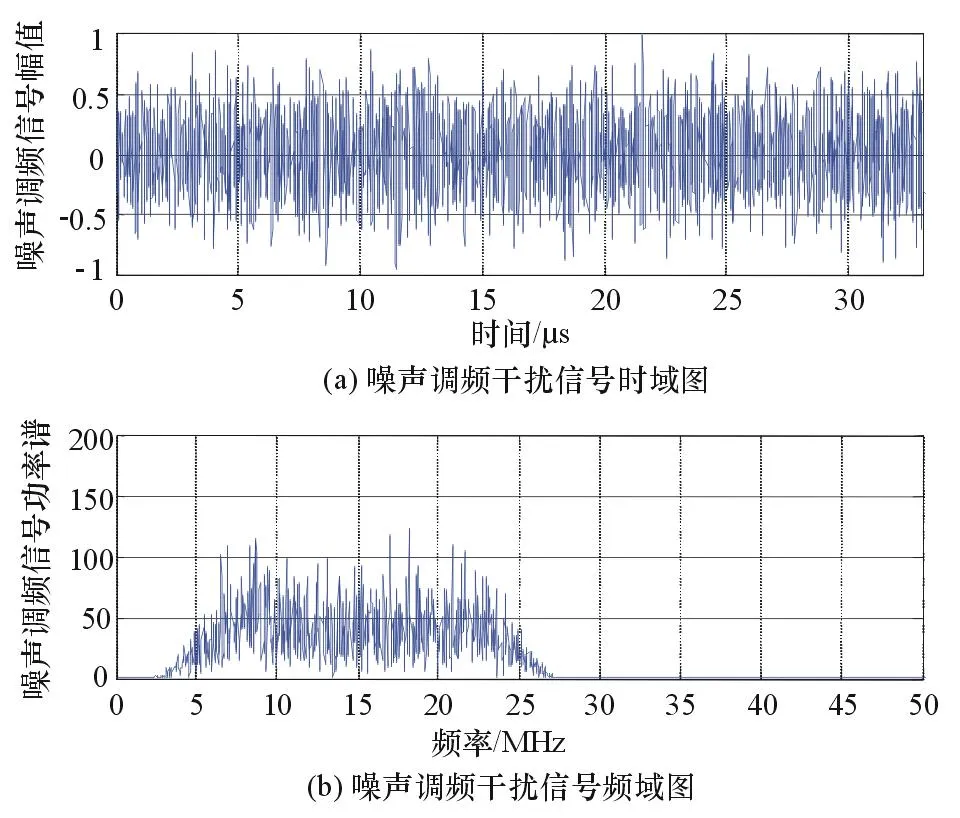
图1 干扰信号时频图
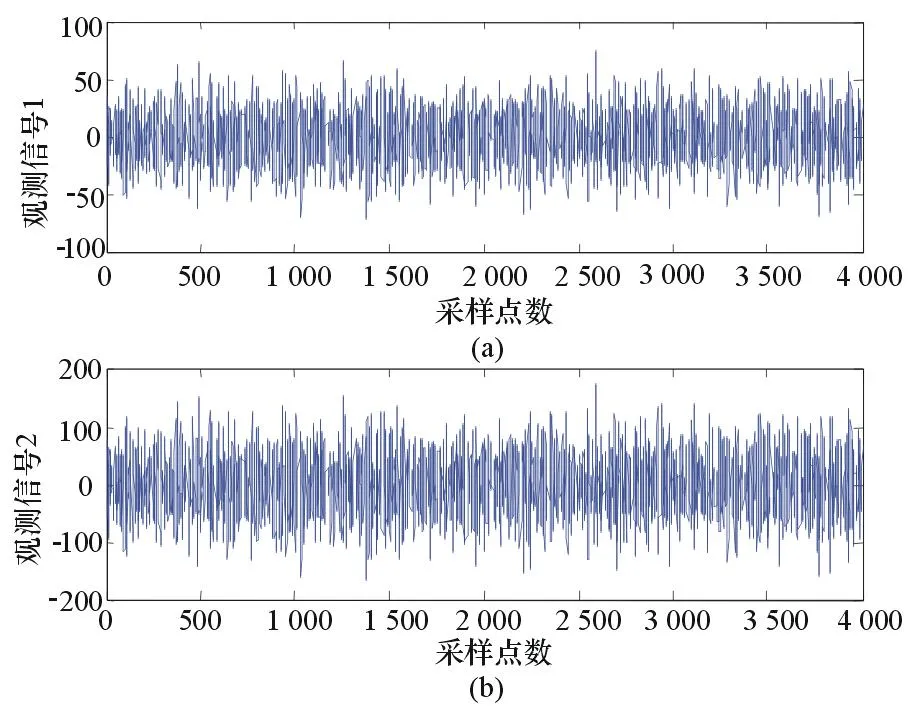
图2 雷达接收机观测信号
在含有噪声以及高功率干扰条件下,目标回波波形失真严重,如不采用相关抑制算法将得到如图3所示的处理效果图,无法得到目标参数。图4将采用传统的基于最大信噪比盲源分离算法进行干扰抑制处理。
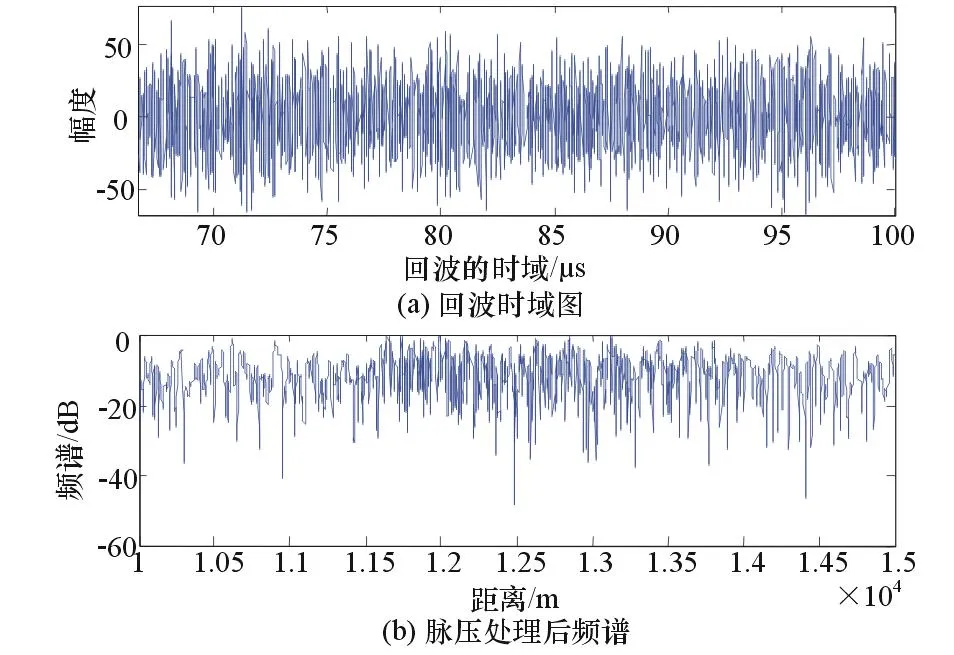
图3 传统算法抑制效果图4最大信噪比盲源分离效果
图4是30dB干信比下,雷达接收机接收到的信号经过最大信噪比盲源分离算法后分离出的2路信号:一路是干扰信号,另一路是目标回波信号,发现经过分离之后的有用信号波形接近时移后的雷达发射波形,为了证明该信号就是目标回波信号,接着进行了脉压处理得到图5。
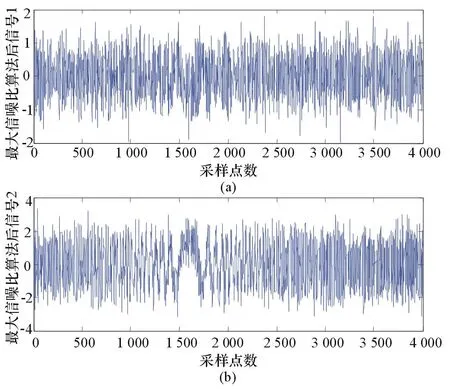
图4 最大信噪比盲源分离效果
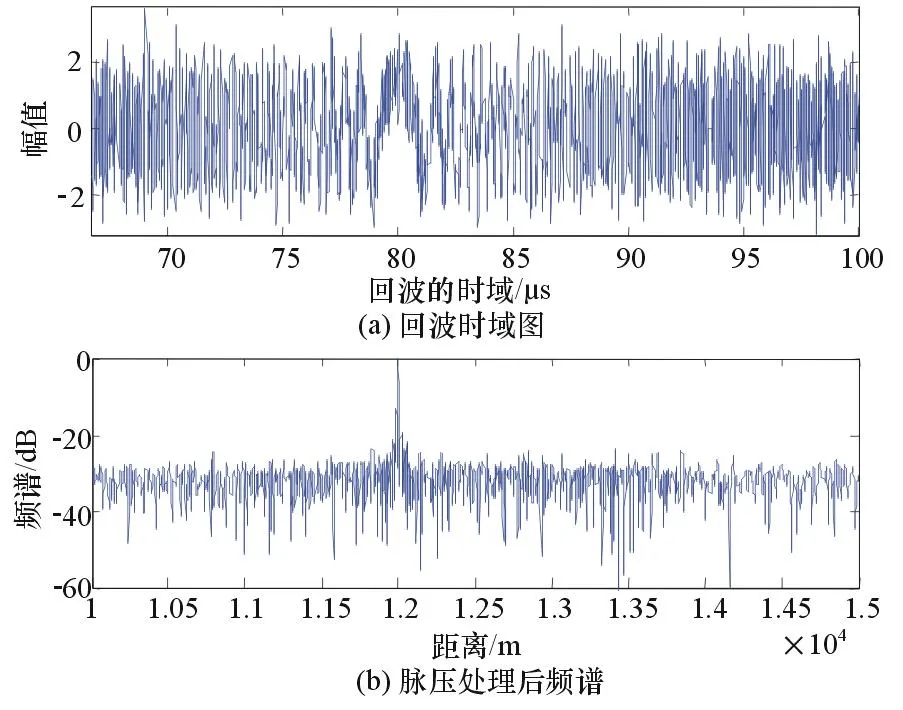
图5 最大信噪比分离后脉压效果
图5是传统的最大信噪比盲源分离算法分离出的结果,噪声起伏较大。图6是经过了改进的基于干扰重构的最大信噪比盲源分离算法,对比图5可以发现波形质量较高,为了定量地比较两算法优劣,引入了相关系数作为参数,比较两者分离出的信号与雷达发射信号的相关程度,仿真如图7所示。
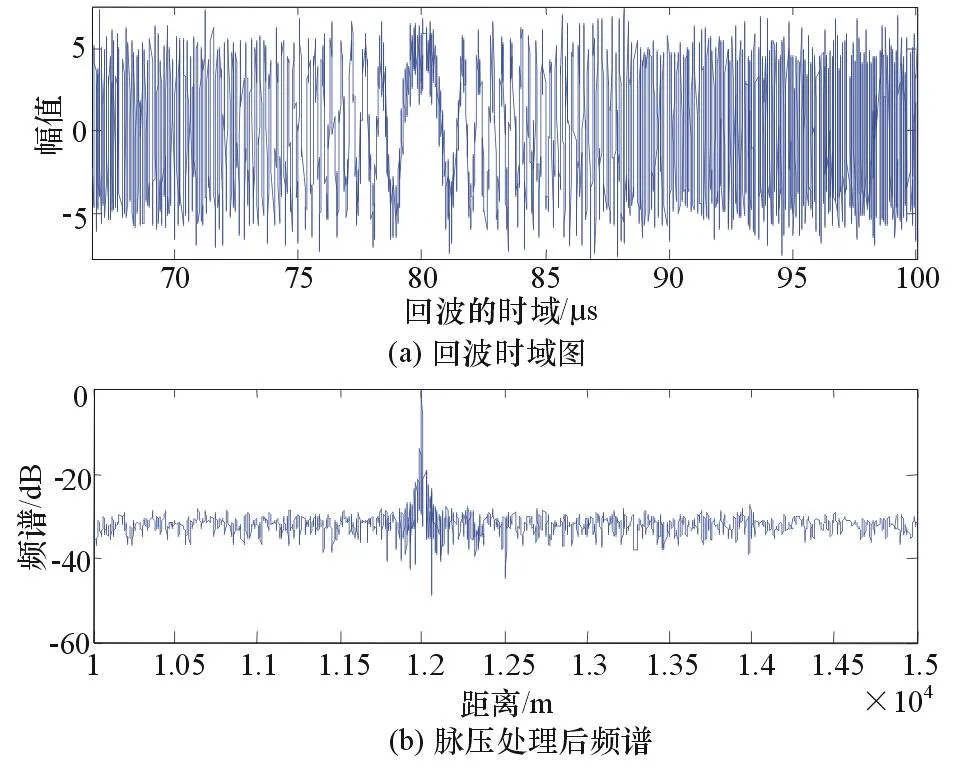
图6 改进后的分离算法脉压效果

图7 算法改进前后相关系数对比
从仿真结果可以得出:基于最大信噪比的盲源分离算法能很好地探测目标物距离为12 000m。但使用干扰重构的最大信噪比分离算法分离出的信号与源信号相关度更大,即分离效果更好;在运算复杂度方面,两者处于同一量级,改进型算法并没有增大运算量。
5结束语
本文提出的使用干扰重构作为最大信噪比盲源分离算法中的源信号估测的方法,使得信号预测比单纯的滑动平均处理效果更好,进而后续分离出的信号质量也更高,与源信号的相似度更大。但本文只选取了噪声调频干扰信号,对其他压制式干扰抑制效果较差,这时可以使用最小均方差(LMS)滤波算法代替滑动平均,能得到相似的结果。
参考文献
[1]赵国庆.雷达对抗原理[M].2版.西安:西安电子科技大学出版社,2012:122-151.
[2]HYVARINENA.独立成分分析[M].周宗潭,董国华,徐昕,等译.北京:电子工业出版社,2014:142- 178.
[3]COMONP.Separationofstochasticprocess[C]//WorkshoponHighorderSpectrumAnalysis.Colorado,1989:174-179.
[4]冯大政.保铮.张贤达.信号盲分离问题多阶段分解算法[J].自然科学进展,2002,12(3):324-328.
[5]HERAULTJ,JUTTENC.Spaceortimeadaptivesignalprocessingbyneuralnetworkmodel[C]//AmericanInsitituteforPhysics:NeuralNetworksforComputingAIPconfProceeding151.NewYork:AmericanInsitituteforPhysics,1986:13-16.
[6]STONEJV.Blindsourceseparationusingtemporalpredictability[J].NeuralComputation,2001(7):150- 165.
[7]张小兵.马建仓.陈翠华.刘恒.基于最大信噪比的盲源分离算法.计算机仿真,2006(10):72-75.
[8]杜东平.雷达压制式干扰抑制算法研究[D].成都:电子科技大学,2008:78-83.
[9]黄高明.盲信号处理及其在无源探测中的应用研究[D].南京:东南大学,2005:1-8.
[10]BORGAM.LearningMultidimensionalSignalProcessing[D].Linkoping,Sweden:LinkopingUniversity,1998.
Research into Anti-blanket Jamming Technology Based on Improved Maximum SNR Algorithm
WANG Yu
(Xidian University,Xi'an 710071,China)
Abstract:Since there are radars,anti-jamming capability is always the key index to evaluate a radar,especially with the increasing complication of battlefield electromagnetic environment,anti-jamming problem of radar becomes particularly important.For anti-blanket jamming,this paper improves the blind source separation algorithm based on traditional maximum signal to noise ratio,presents the method that uses jamming remodelment algorithm to replace the slide average treatment method, then gets the radar signal of better quality than by traditional method,and the correlation between the output signal and the source signal is stronger.
Key words:anti-blanket jamming;blind source separation;maximum signal to noise ratio;jamming remodelment
DOI:10.16426/j.cnki.jcdzdk.2016.01.006
中图分类号:TN974
文献标识码:A
文章编号:CN32-1413(2016)01-0031-05
收稿日期:2015-11-03
