一维Allen-Cahn方程有限差分方法的离散最大化原则和能量稳定性研究
2016-04-27张佳琪侯天亮
张佳琪,侯天亮
(北华大学数学与统计学院,吉林 吉林 132013)
一维Allen-Cahn方程有限差分方法的离散最大化原则和能量稳定性研究
张佳琪,侯天亮
(北华大学数学与统计学院,吉林 吉林132013)
摘要:研究了一维Allen-Cahn方程有限差分方法逼近.空间方向采用中心有限差分格式,而时间方向分别采用带稳定项的一阶线性隐显格式、二阶非线性校正Crank-Nicolson格式和二阶线性Leap-Frog格式.证明了数值格式的离散最大化原则和能量稳定性.
关键词:Allen-Cahn方程;有限差分方法;最大化原则;能量稳定性
【引用格式】张佳琪,侯天亮.一维Allen-Cahn方程有限差分方法的离散最大化原则和能量稳定性研究[J].北华大学学报(自然科学版),2016,17(2):159-164.
1引言
相场模型是由偏微分方程描述的数学模型,具有非常丰富的数学内涵,因其相当复杂,迄今为止我们还没有能够完全了解它们.相场的数值模拟一直是国内外研究的一个热门而重要的领域,并推动微分方程数值解理论乃至其他数学理论的深入发展,具有重要的理论意义与实际意义.
1979年,为了描述晶体中反相位边界运动,Allen和Cahn[1]引入了Allen-Cahn方程.由于此类相场模型没有真解,所以采用不同的数值方法来进行模拟就显得尤为重要.目前关于这些相场模型的数值逼近已有很多工作,包括有限差分方法、有限元方法和谱方法等.文献[2]中,作者针对两种流体的Allen-Cahn 型相场模型提出了一种自适应移动网格方法,数值实验表明移动网格算法在提高分辨率和计算效率方面非常有效;徐玲玲[3]主要考虑一维和二维Allen-Cahn方程Neumann条件边值问题,提出半隐的全离散耗散有限差分格式,并且将其推广到一维 Cahn-Hilliard方程;文献[4]则考虑Allen-Cahn方程的局部间断Galerkin有限元方法,数值试验验证了此方法的有效性;Feng和Prohl[5]提出了Allen-Cahn方程的半离散有限元格式和一阶全离散有限元格式,并获得先验误差估计.据我们所知,针对Allen-Cahn方程的数值逼近,没有严格的数值解的最大模稳定性分析.
众所周知,Allen-Cahn方程满足最大化原则和能量稳定性(参见文献[6]),那么这些性质对数值逼近解是否成立呢? 本文利用有限差分方法求解一维Allen-Cahn方程,给出3种时间离散格式,主要研究两方面内容:一方面是离散最大化原则:如果问题初值被1控制,那么数值解也可以被1控制;另一方面是离散能量稳定性:定义的离散能量递减.
2有限差分逼近
我们研究下面一维Allen-Cahn方程的数值逼近

(1)
u(x,0)=u0(x), x∈Ι,
(2)
(3)
这里I为实数空间中的有界闭区间,u表示二元合金中一个金属部件的浓度,参数ε>0表示接口宽度,非线性项f(u)=u-u3.
首先,空间导数采用二阶中心差分格式离散,令Dh表示相应离散矩阵,表示为
这里N表示空间离散后区间内部节点个数,h表示空间步长.
在空间离散后,接着考虑下面3个时间离散格式:
(ⅰ)稳定的一阶线性隐显格式
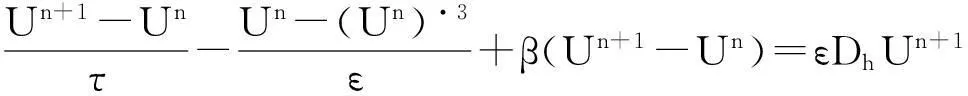
(4)


(ⅱ)稳定的二阶非线性校正Crank-Nicolson格式

(5)
这里


格式(5)等价于
(6)
其中

(ⅲ)稳定的二阶线性Leap-Frog格式
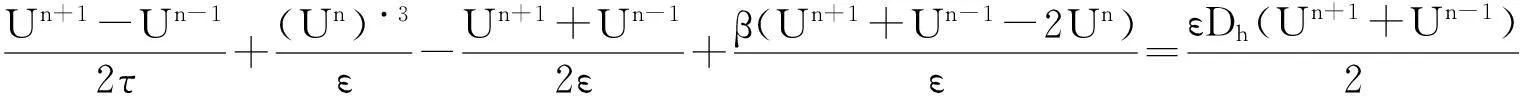
(7)
这里n≥1,β表示稳定项系数.对于时间第一层上的数值解,应用格式(6)进行求解.
3离散最大化原则


由格式(4)知
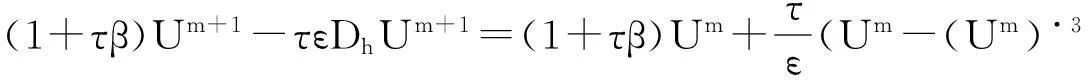
(8)

注意到上式右边项的元素具有下面的函数形式

容易看到


综上可知
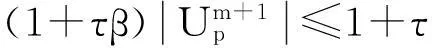
由式(6)整理得

(9)

接下来,类似定理1中的证明,可以推出
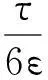
由以上估计可推出

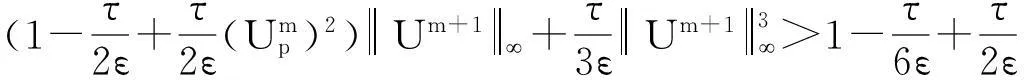
由以上两个式子可以推出
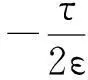
由式(7)整理得
(10)
(11)



(12)
结合式(11)和(12),我们有
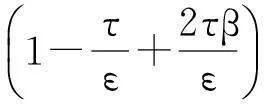
证毕.
4离散能量稳定性
我们定义如下的离散能量:

下面,我们将证明格式(4)和(5)满足离散能量稳定性.
定理4假设定理1中的条件成立,格式(4)求得的数值解可以保证离散能量递减,即
E(Un+1)≤E(Un),n=0,1,….
(13)
证明:将式(4)两边左乘(Un+1-Un)T,得

(14)
把两个时间层上的离散能量相减得
(15)
对任意的a,b∈[-1,1],下面不等式成立:

由于矩阵Dh是对称负定的,容易看到

因此,由上面两个不等式推出

定理5对任意的时间步长τ>0,格式(5)求得的数值解可以保证离散能量递减,即
E(Un+1)≤E(Un),n=0,1,….
证明:在等式(5)两边左乘(Un+1-Un)T,得
因为矩阵Dh是对称的,我们有
(Un+1-Un)TDh(Un+1+Un)=(Un+1)TDhUn+1-(Un)TDhUn.
由上面两个等式以及式(15)可推出

证毕.
参考文献:
[1] S M Allen,J W Cahn.A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening[J].Acta Metall,1979,27:1085-1095.
[2] 成彬,刘波,王冬艳,等.Allen-Cahn型相场模型的移动网格方法[J].河北科技大学学报,2011,32(2):110-114.
[3] 徐玲玲.Allen-Cahn方程Neumann边值问题的的二阶耗散差分格式[D].上海:上海交通大学,2010.
[4] 于春丽.Allen-Cahn方程的局部间断Galerkin有限元方法[D].济南:山东大学,2009.
[5] X B Feng,A Prohl.Numerical analysis of the Allen-Cahn equation and approximation for mean curvature[J].Numer Math,2003,27(99):33-65.
[6] L C Evans,H M Soner,P E Souganidis.Phase transitions and generalized motion by mean curvature[J].Commun Pure Appl Math,1992,45:1097-1123.
【责任编辑:伍林】
Discrete Maximum Principle and Energy Stability of Finite Difference Methods for One-dimensional Allen-Cahn Equations
Zhang Jiaqi,Hou Tianliang
(SchoolofMathematicsandStatistics,BeihuaUniversity,Jilin132013,China)
Abstract:The finite difference approximation for one-dimensional Allen-Cahn equation is studied.Central finite difference scheme is used for spatial discretization,stabilized one-order linear implicit-explicit scheme,second-order nonlinear modified Crank-Nicolson scheme and second-order linear Leap-Frog scheme are used for temporal discretization respectively.Discrete maximum principle and energy stability of these schemes are established.
Key words:Allen-Cahn equation;finite difference method;maximum principle;energy stability
中图分类号:O241.5
文献标志码:A
作者简介:张佳琪(1992-),女,硕士研究生,主要从事偏微分方程数值解法研究,E-mail:zjqss1992@163.com;通信作者:侯天亮(1985-),男,博士,讲师,硕士生导师,主要从事偏微分方程数值解法研究,E-mail:htlchb@163.com.
基金项目:国家自然科学基金项目(11526036).
收稿日期:2015-12-18
文章编号:1009-4822(2016)02-0159-06
DOI:10.11713/j.issn.1009-4822.2016.02.004
