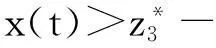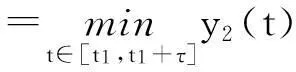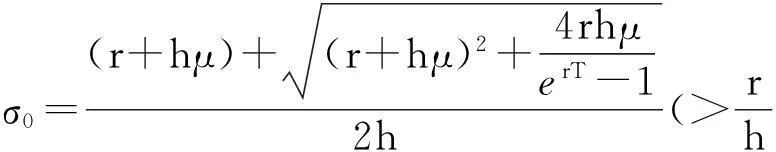一类具有阶段结构且被连续收获的时滞B-D捕食模型
2016-04-27张慧勤贾建文
张慧勤,贾建文
(1.运城师范高等专科学校,山西 运城 044000;2.山西师范大学数学与计算机科学学院,山西 临汾 041004)
一类具有阶段结构且被连续收获的时滞B-D捕食模型
张慧勤1,贾建文2
(1.运城师范高等专科学校,山西 运城044000;2.山西师范大学数学与计算机科学学院,山西 临汾041004)
摘要:研究了一类捕食者具有阶段结构且被连续收获的具有时滞的Beddington-Deangelis捕食模型.应用脉冲微分方程比较定理,获得了捕食者灭绝周期解全局吸引的充分条件以及系统持久的充分条件.
关键词:时滞;阶段结构;脉冲;全局吸引性;持久性
【引用格式】张慧勤,贾建文.一类具有阶段结构且被连续收获的时滞B-D捕食模型[J].北华大学学报(自然科学版),2016,17(2):148-153.
1模型建立
在自然界中,有很多种群的个体的生命历程会经历幼年和成年两个阶段,在研究这些种群时把它们分成两个不同的阶段更加符合实际情况,因此,阶段结构模型引起了人们的极大兴趣[1-2].同时,一个个体从幼年成长到成年也需要一定的时间,因此,时滞也是一个不可忽略的因素[3-4].近些年来,与可持续发展直接相关的可再生资源最优化管理问题已经有很多学者进行了广泛的研究[5-6].
本文研究一类食饵具有脉冲扰动、捕食者被连续收获的具有时滞和阶段结构的Beddington-Deangelis 捕食模型:
(1)
初始条件为


本文中假设幼年捕食者不具有捕食能力.考虑到实际的生物意义,我们仅在D={(x,y1,y2)∈3x,y1,y2≥0}上研究系统(1).
因为系统(1)的第1个方程和第3个方程不包含y1(t),所以我们可以把系统(1)简化为
(2)
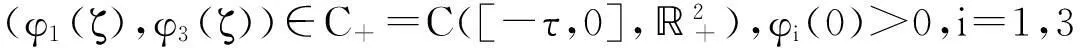
2相关引理
引理1[6]脉冲微分方程
其中a>0,b>0,μ>0,n为正整数,有唯一一个全局吸引的正周期解


引理2[4]考虑方程
x′(t)=ax(t-τ)-bx(t)-cx2(t),
其中a,b,c和τ都是正的常数,并且对任意的t∈[-τ,0],都有x(t)>0.则有如下结论:

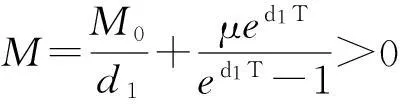
证明:定义 V(t)=λx(t)+y1(t)+y2(t),则
考虑下面的脉冲微分方程

3捕食者灭绝周期解及其全局吸引性

因为
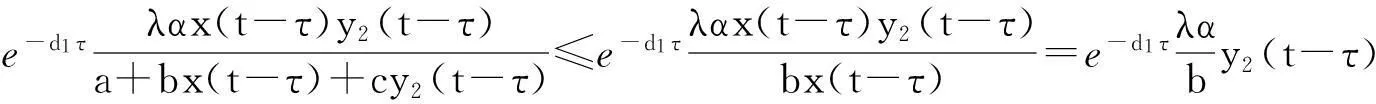
由上式和系统(2)的第2个方程,有
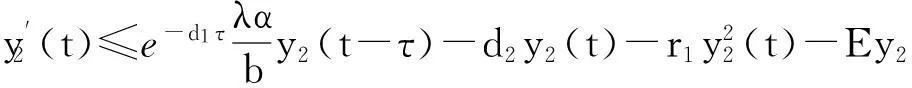
考虑下面的比较方程
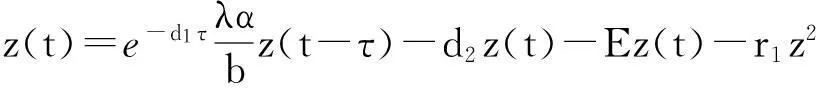
由此可知,对任意的ε1>0,存在T1,使得当t>T1+τ时,有y2(t)<ε1.
结合上面的结论和系统(2)的第1个方程,可得

由此,我们得到z1(t)≤x(t)≤z2(t),并且当t→+时,(t).这里,z1(t)和 z2(t)分别为脉冲方程



4系统的持久性
证明:系统(2)的第2个方程可以写成


根据引理3可以得到
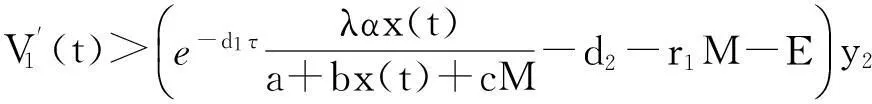
(3)
由定理2的条件可知,我们可以选择足够小的y0>0,ε>0使得
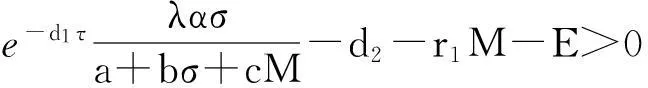
(4)
我们断言:对任意的t0>0,当t≥t0时,y2(t) (5) 因此,由系统(2)的第2个方程及x(t)>σ可得 由此便得出矛盾.从而证明了当t≥t1时,有y2(t)≥y*. 由式(5)和y2(t)≥y*,对任意的t≥t1,有 至此,我们证明了对于任意的t0>0,当t≥t0时,式子y2(t) 根据上述断言,那么就只存在两种情形: (ⅰ)对于充分大的t,有y2(t)>y0. (ⅱ)对于充分大的t,有y2(t)在y0处振动. 此时,存在正的常数t*和δ,使得y2(t*)=y2(t*+δ)=y0,并且当t* 如果δ>τ,则当t* 因为区间[t*,t*+δ]是任意选取的,因此,对于足够大的t,我们有y2(t)>q.证毕. 证明:设(x(t),y1(t),y2(t))是系统(1)的任意解.由系统(1)的第1个方程,得 根据比较定理[7]和引理 1可得:对任意的ε0>0,当t→+时,有,其中 , 结合定理 2可知系统(1)是持久的.证毕. 5生物意义 根据生物资源管理的实际情况,本文我们考虑了捕食者具有阶段结构且被连续收获的具有时滞的B-D捕食模型.其中食饵具有脉冲输入,且对捕食者进行连续捕获.我们分析了系统(1)的捕食者灭绝周期解的全局吸引性,并且得到了系统(1)持续生存的条件.研究结果表明:捕食者的捕获量E和对食饵的脉冲投放量μ对系统(1)的持久性起着重要作用,即其能阻止捕食者的灭绝,可以对生态平衡起到保护作用. 参考文献: [1] Y N Xiao,L S Chen.Global stability a of a predator-prey system with stage structure for the predator[J].Acta Math Sin Engl Ser,2003,19:1-11. [2] S A Gourley,Y Kuang.A stage structure predator-prey model and its dependence on maturation delay and deathrate[J].J Math Biol,2004,49:188-200. [3] J B Bence,R M Nisbet.Space limited recruitment in open systems:the importance of time delays[J].Ecology,1989,70:1434-1441. [4] X Y Song,L S Chen.Optimal harvesting and stability for a two species competitive system with stage structure[J].Math Biosci,2001,170:173-186. [5] J J Jiao,X Z Meng,L S Chen.Harvesting policy for a delayed stage structured Holling II predator-prey model with impulsive stocking on prey[J].Chaos Solutions Fract,2009,41(1):103-112. [6] L Z Dong,L S Chen,L H Sun.Extinction and permanence of the predator-prey system with stocking on the prey and harvesting on the predator impulsively[J].Math Methods Appl Sci,2006,29:415-425. [7] V Lakshmikantham,D D Bainov,P Simronov.Theory of impulsive differential equations[M].Singapore:World Scientific,1989. 【责任编辑:伍林】 A Stage-structured B-D Predator-prey Model with Impulsive Stocking and Continuous Harvesting Zhang Huiqin1,Jia Jianwen2 (1.YunchengAdvancedNormalCollege,Yuncheng044000,China;2.SchoolofMathematicalandComputerScience,ShanxiNormalUniversity,Linfen041004,China) Abstract:A delayed stage-structured B-D predator-prey model with impulsive stocking on prey and continuous harvesting on predator is investigated.Using the comparison theorem of impulsive differential equations,we obtained the sufficient conditions for the global attractivity of the predator-eradication periodic solution and the permanence of the system. Key words:delay;stage-structure;impulsive;globally attractivity;permanence 中图分类号:O175.1 文献标志码:A 作者简介:张慧勤(1983-),女,硕士,讲师,主要从事生态数学研究,E-mail:103724782@qq.com;贾建文(1963-),男,教授,硕士生导师,主要从事生态数学研究,E-mail:jiajw.2008@163.com. 基金项目:山西省自然科学基金资助项目(2013011002-2). 收稿日期:2015-12-25 文章编号:1009-4822(2016)02-0148-06 DOI:10.11713/j.issn.1009-4822.2016.02.002