车辆内轮差问题的优化分析

范朔

【摘 要】由于车辆内轮差的存在而导致的交通事故屡见不鲜。对于大型车辆或是狭窄路况此问题尤为严重。通过建立数学模型，借助MATLAB，可以模拟绘制车辆转弯时前、后内侧车轮的运动轨迹，制作车辆转弯过程动画，分析车辆各参数与内轮差的关系，进而提出由车辆内轮差导致的相关安全问题的解决方案，尽量减少和避免此类事故的继续发生。

【关键词】MATLAB；内轮差；数学建模；事故防范

Optimal Analysis in Difference of Radius Between Inner Wheels

FAN Shuo

（School of Mechanical and Power Engineering， East China University of Science and Technology， Shanghai 200237， China）

【Abstract】Traffic accidents caused by the existence of difference of radius between inner wheels always occur. The problem is particularly severe with large vehicles and narrow roads condition. By establishing mathematics model and with the help of MATLAB， the path of front and back wheels of vehicles when turning can be simulated， the animation of vehicles when turning can also be made， so that relationship between different parameters of vehicles and difference of radius between inner wheels can be concluded. Whats more， solutions which aiming at reducing and eliminating the occurrence of traffic accidents caused by difference of radius between inner wheels can be proposed.

【Key words】MATLAB； Difference of radius between inner wheels； Mathematical model； Prevention of accidents

0 引言

车辆内轮差指车辆转弯时前内轮转弯半径与后内轮转弯半径之差。通常车辆前内轮的转弯半径大于后内轮，这也就意味着如果车辆的车头部分以较小的转弯半径转弯时，车辆的中、后部分会以一个更小的转弯半径转弯，即车辆在转弯的过程中会向圆心方向的空间不断靠近。而这种在转弯过程中的变化通常难以被驾车司机察觉，造成司机的“视觉盲区”。容易理解，倘若在“视觉盲区”内存在行人或是其他机动车辆，事故发生的可能性将大大提高。实际上，由于内轮差的存在而造成的交通事故屡见不鲜。对于大型车辆或是狭窄转弯路况而言，此问题尤为严重。

若结合生活经验定性的思考一下内轮差问题，不难想象对于同一类车型，转弯的幅度越小，内轮差越小，反之相反。而对于不同的车型，当转弯的幅度相同时，轴距大的车型内轮差大，反之相反。但是从经验角度没有办法推出一个具体的内轮差数值概念。本文希望通过建立数学模型，借助MATLAB，定量求解内轮差问题，增加人们对于内论差的认知。在建模的过程中，与其他转弯问题研究一样[1，2]，我们忽略离心力所引起的侧滑与轮胎变形所引起的侧向偏离对运动轨迹的影响。

1 内轮差建模

1.1 模型一

假设1：汽车整体为一刚体，转弯的过程中不会发生变形；

假设2：车辆在转弯过程中，内前轮与内后轮的轨迹均为圆弧，且两圆弧圆心重合。

当rD为车辆的最小转弯半径时，对应的D即为该车的最大内轮差。最小转弯半径的数值可以从车辆参数表中方便的获得，因此利用式（3）可以快速估算车辆的最大内轮差。

但由于真实条件下车辆的转弯轨迹并不是严格的圆弧，因此上述公式实际上计算的是车辆内轮差的近似值。不过有研究表明[3]，利用该公式计算的结果与实测数据的误差小于10%。因此，上述公式不失为快速估算内轮差的好方法。接下来寻找更为精确的建模方法。

1.2 模型二

假设1：汽车整体为一刚体，转弯的过程中不会发生变形；

假设2：汽车内前轮的运动轨迹为圆弧，内后轮的轨迹由前轮的运动而定；

在模型一中我们将内侧前、后轮的轨迹都假定为圆弧，但由于在车辆转弯过程中只有前轮起导向作用，所以实际上后轮的运动轨迹是受前轮带动而被动确定的，并不是按圆弧运动。因此在模型二中我们只假定前轮的转弯轨迹为圆弧，借助其他条件求解后轮的轨迹。

首先，车辆在转弯过程中轴距并不发生改变，即内前轮（A）、后轮（B）之间的距离不发生改变，因此有：

此微分方程系统我们可以借助MATLAB快速求解、绘图。

现假设汽车内侧前轮按xA=7cost；yA=7sint运动，汽车的轴距l为4米。MATLAB给出的转弯轨迹如下：

图2 模型二MATLAB作图结果

从图2中可以看出，内后轮的轨迹并不是圆弧。图中两条曲线所夹区域即为由内轮差造成的转弯过程中车辆发生的偏移区域，也即“视觉盲区”。倘若行人或其他车辆出现在此区域，则事故发生率将大大提高。在MATLAB辅助下，内轮差问题变得形象而直观。前后轮的轨迹方程可以通过MATLAB进行拟合获得，进而可以计算如盲区面积等其他信息。

下面尝试用控制变量的方法，首先控制车辆的转弯半径相同，在同一幅图中绘出不同轴距车辆的内轮转弯轨迹，如图3（a）所示。再控制车辆的轴距相同，在同一幅图中绘出不同转弯半径车辆的内轮转弯轨迹，如图3（b）所示。这两幅图再次说明：内轮差随轴距和转弯幅度的增大而增大。这也从理论上更为形象的阐明了为何如公交车、渣土车等长轴距车更容易在转弯的过程中酿成事故。

（a）不同轴距汽车以相同转弯半径转弯的内轮轨迹图

（b）相同轴距汽车按不同转弯半径转弯的内轮轨迹图

图3

借助模型二，对参数已知的车辆（转弯半径及轴距），我们可以利用MATLAB快速模拟绘制出车辆转弯过程中所形成的“视觉盲区”，拟合轮胎运动轨迹方程，计算盲区面积等。广大车辆驾驶员若能由此建立起转弯过程中的警惕意识，将对事故的预防具有积极的意义。广大群众由此也应得到相应的启示：切忌距离转弯车辆过近，尤其是长轴距车辆或是急转弯车辆。

不过模型二与真实条件相比依然存在缺陷。在模型二中我们假设前轮的运动轨迹为圆弧，但是实际上在转弯的过程中司机通常进行的是“先打轮，再回轮”的操作，也就是说前轮的转弯半径应是先减小而后增大的，并不保持定值。因此在模型三中我们将尝试对模型二进行改进，重新假定前轮的运动轨迹，并验证模型二中建立的微分方程系统是否依然适用。

1.3 模型三

假设1：汽车整体为一刚体，转弯的过程中不会发生变形；

假设2：汽车内前轮的转弯半径按一定规律变化，不保持定值。内后轮的轨迹依然由前轮的运动而定；

根据车辆内前轮在转弯过程中曲率半径先增大后减小的规律，我们在模型二的基础上假定内前轮的运动轨迹为：

经分析可知，该函数在0≤t≤π/4的区间时，随着t的增大，函数的曲率半径逐渐增大，并在t=π/4时达到最大值。当π/4≤t≤π/2时，函数的曲率半径随t的增大而减小。其变化规律与实际汽车转弯曲率半径变化规律一致，因此以该函数作为汽车内前轮的轨迹方程做进一步分析。

图4 模型二与模型三内前轮轨迹对比图

仿照模型二建立微分方程系统，借助MATLAB求解并绘制在该种假设下内侧前、后轮的轨迹图，将其与模型二所绘车轮轨迹进行比较：

图5 模型二与模型三内轮转弯轨迹对比图

理论上模型三所示轨迹更接近于车辆实际转弯过程中的内轮轨迹。模型三的建立也同时说明了模型二中所使用的微分方程系统具有很好的可迁移性。因此，倘若需要实际条件下准确的车辆内轮轨迹，通过记录车辆转弯过程中的车轮位置信息，拟合出内侧前轮的轨迹方程，套用模型二中的微分方程系统，即可实现。

此外，笔者除利用MATLAB模拟绘制了车辆内轮的转弯轨迹外，还借助其动画制作功能制作了内轮差形成的动画。笔者认为通过动画可以更加形象的帮助理解由于内轮差的存在而导致的内侧前、后轮轨迹的形成过程。若未来能将动画或是轨迹图像应用于针对内轮差问题的相关教学中，将会收到很好的效果。

2 总结

文章中所建立的三个内轮差模型各有特点。模型一可方便的对内轮差进行估算，而在MATLAB的辅助下，模型二和模型三则可以更加准确的描述内轮差问题。但需注意的是，本文中的三个模型只针对可视作刚体的车辆。

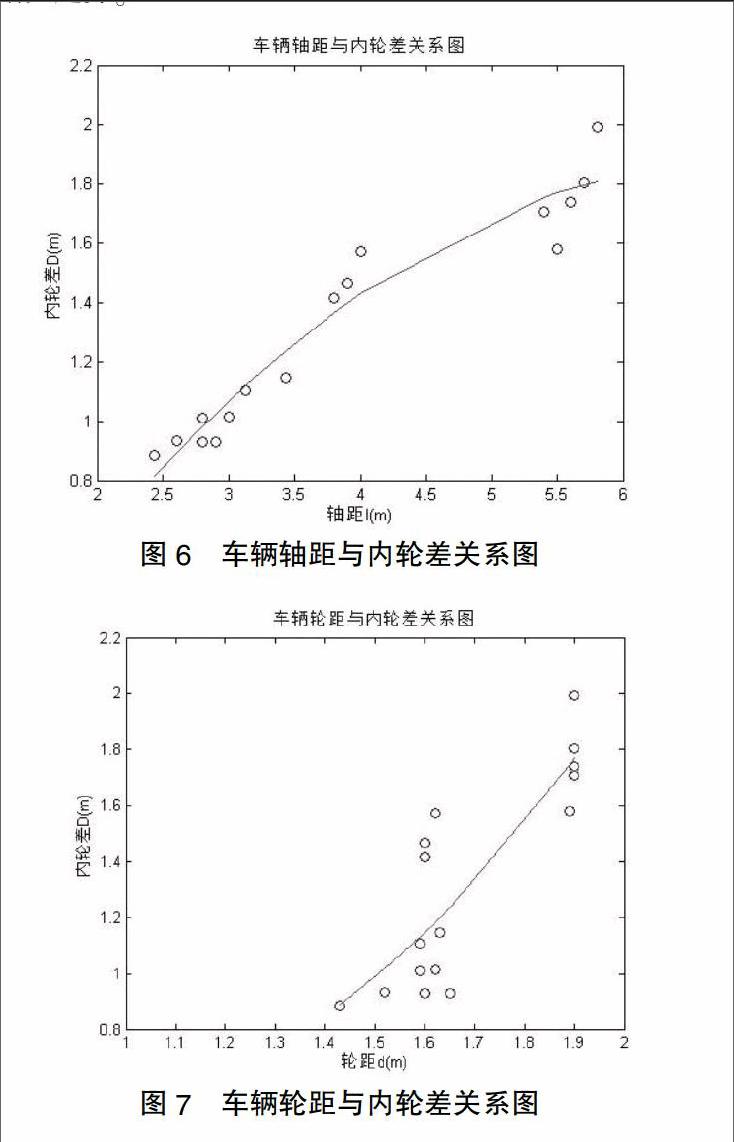
通过查阅几类车型的汽车参数表，利用MATLAB绘制了车辆轴距与内轮差的关系图（图6），从图中可以明显看出：随轴距增大内轮差也增大。同时还绘制了车辆轮距和最小转弯半径与内轮差的关系图（图7、图8），可以看出内轮差随轮距和最小转弯半径的增大也呈现出明显的增大趋势。

图6 车辆轴距与内轮差关系图

图7 车辆轮距与内轮差关系图

对内轮差问题的研究主要是为了更好的预防由于内轮差而引起的交通事故的发生。经估算，对轴距不超过3m的小型车而言，其内轮差一般不会超过1m，约为0.8m至1m；对轴距在3m至5m的中型车而言，其内轮差增大，约为1m至1.5m；对于轴距超过5m的大型车而言，其内轮差则可能达到2m甚至以上。掌握这些数据对避免事故的发生有着重要意义。于行人而言，应尽量远离正在过弯中的车辆，尤其是公交车等大型车辆，并至少保持2m以上的安全距离。于驾驶者而言，应充分考虑到所驾车型轴距，最好估算出所驾车型内轮差，提前观察转弯内侧是否有其他机动车辆或行人活动，控制车的转向角度。尤其是行驶在傍山险路或是临崖路段，若忽视内轮差后果将极为严重，相关事故曾有过记载[4]。此外有研究指出[5]，车速对驾驶者的视野会造成影响：车辆静止状态下，驾驶员双眼的视野范围约210°；40km/h，双眼的视野范围约100°；70km/h，双眼的视野范围约65°；100°km/h，双眼的视野范围只约40°。因此转弯的过程中减速慢行也更有利于驾驶者观察路况，避免交通事故的发生。

图8 车辆最小转弯半径与内轮差关系图

此外，借助该问题的研究，可以发现MATLAB对于求解微分方程系统的极大帮助。不只是运动学，诸多领域中的系统，如生物反应过程、化学反应速率、电子系统等都可以通过微分方程进行描述，这也就意味着可以利用MATLAB辅助研究这些问题。通过计算机编程，不仅可以方便的计算复杂的实际问题，同时可以将结果可视化[6]。因此，MATLAB作为强大的数学软件，无论对于工程实践或是教学都具有很高价值，应当更加普及与推广。

【参考文献】

[1]萧建英.汽车及汽车列车转弯过程的研究[J].汽车技术，1986（08）：25-27.

[2]李相彬.汽车列车转弯过程的分析及其最小转弯半径的确定[J].汽车技术，1981（11）：18-21.

[3]陈思嘉，巫宇霞，杨平.汽车转弯时由内轮差引发的交通事故原因建模与分析[J].数学通报，2013（12）：55-57.

[4]阿仁.内轮差与外轮差[J].汽车驾驶员，1998（8）：15.

[5]万禄义.公交车“内轮差”，不容忽视[J].人民公交，2012（1）：71.

[6]李彤，阚文彬，曹昱彭.学习MATLAB应从大一开始[J].实验技术与管理，2008（8）：102-104.

[7]Holly Moore. MATLAB实用教程[M].高会生，刘童娜，李聪聪，译.北京：电子工业出版社，2010.

[8]王铎.理论力学[M].哈尔滨：哈尔滨工业大学出版社，2003.

[9]张志涌.MATLAB教程R2012a[M].北京：北京航空航天大学出版社，2010.

[责任编辑：汤静]