基于刀盘摩擦扭矩参数的刀具磨损状态识别

左翠凤， 唐德高， 戎晓力， 廖　斌

(解放军理工大学爆炸冲击防灾减灾国家重点实验室， 江苏 南京　210007)



基于刀盘摩擦扭矩参数的刀具磨损状态识别

左翠凤， 唐德高， 戎晓力， 廖斌

(解放军理工大学爆炸冲击防灾减灾国家重点实验室， 江苏 南京210007)

摘要：盾构在砂卵石地层掘进时，刀具磨损量大一直是困扰施工的难题。从土压平衡盾构的工作原理及砂卵石地层特性2方面分析刀盘扭矩的构成，并通过数学和力学分析建立了摩擦扭矩计算模型。以成都地铁3号线红牌楼南站—红牌楼站区间为研究背景，依托盾构施工安全风险监控系统，对计算模型进行验证；分析刀具磨损时，根据地质条件将摩擦扭矩进行分段计算，同时将摩擦扭矩除以总扭矩得到摩擦比例系数，运用比例系数跟踪判断刀具磨损程度。研究结果表明，砂卵石地层中构成刀盘扭矩的主要组分是刀盘正面、背面和侧面上的摩擦扭矩；摩擦扭矩计算模型符合工程实际；得到的摩擦比例系数与换刀形态具有较好的对应性，可定性判断刀具磨损程度，指导工程实践。

关键词：砂卵石地层； 土压平衡盾构； 刀具磨损； 摩擦扭矩； 比例系数

0引言

近年来，盾构法以其对周边居民生活及地面交通影响小、劳动强度低和掘进速度快等优点，成为地铁隧道施工的首选方法。虽然盾构法具有其他工法难以比拟的优越性，但在施工期间依然面临不少问题。成都地铁隧道主要穿越砂卵石地层，其特点是卵石粒径大、摩擦因数大、强度高，并具有高的磨蚀性，导致施工过程中刀具磨损、脱落，换刀频繁。盾构掘进时频繁换刀，会严重影响工程成本和进度，加大施工风险。

以往研究中，学者们主要对岩石地层的盘形滚刀磨损进行了分析。张厚美等[1-3]深入研究了盾构施工中滚刀的损坏机制，并提出利用盾构掘进参数跟踪判断滚刀损坏。杨延栋等[4]基于Rabinowicz磨粒磨损方程和CSM滚刀破岩力模型，通过近似计算和数学推导，建立了滚刀直接磨损的磨损速率和线磨损速率预测模型。针对砂卵石地层施工中所遇到的刀具磨损，主要是从优化刀盘设计和刀具布置角度进行分析[5-6]，很少从施工控制方面进行研究。

盾构在砂卵石地层掘进时刀具磨损后会大大降低其掘进效率，使刀盘的扭矩增大。扭矩作用又会影响到盾构顶进推力、推进速度、刀盘转速及驱动功率等参数[7]。因此，分析砂卵石地层盾构刀具磨损时，刀盘扭矩是关键参数之一。目前，国内许多学者已经进行了不少有关盾构刀盘扭矩的研究[8-10]。

本文在前人研究的基础上，根据砂卵石地层力学特性，分析了土压平衡盾构刀盘扭矩的构成，建立了多层覆土及复合型掌子面工况下的摩擦扭矩计算模型。以成都地铁3号线红牌楼南站—红牌楼站区间为研究对象，对提出的摩擦扭矩计算模型进行验证，并尝试运用刀盘扭矩参数对刀具磨损程度进行定性判断。

1工程背景及实验数据概况

成都地铁3号线1期工程由东北向西南贯穿城市CBD核心区，共设17座车站，线路长20.325 km，全为地下线，平均间距1.227 km。红牌楼南站—红牌楼站(以下简称红红区间)是3号线1期工程的第2个区间，采用盾构法施工。本区间隧道主要覆盖杂填土、粉质黏土、粉土、细砂、松散卵石和稍密卵石，盾构主要在中密卵石和密实卵石土层中穿过。隧道顶面最大埋深21 m，最小埋深14 m。岩土工程勘察报告显示，钻探揭示卵石的最大粒径达200 mm，但可能存在更大粒径的漂石。

目前，在成都地铁项目中研发了盾构施工安全风险监控系统，该系统通过自定义配参功能支持多家盾构进行远程监控，在盾构掘进中自动采集数据并存储于数据库中。本文处理的数据来源于盾构在红红区间左线掘进过程中提取的环号为500—819对应的扭矩值参数。通过对扭矩参数中异常点、缺失点进行分析、清洗，最终得到本文的实验数据。

2施工参数的选择

盾构施工时为保证工程进度和施工安全，人为设定了刀盘转速、掘进速度和螺旋机转速，而刀盘扭矩、推力和贯入度则是人工控制参数设定后的反馈参数。在进行盾构刀盘刀具磨损分析时，主要分析掘进过程中反馈参数的变化。刀具磨损后，掘进效率大大降低，刀盘扭矩增大。扭矩作用又会影响到盾构顶进推力、驱动功率等参数。分析砂卵石地层盾构刀具磨损时，刀盘扭矩是关键参数之一。因此本文选择刀盘扭矩参数对刀具磨损程度进行定性判断。需要说明的是，本文是在渣土改良后的情况下对盾构刀具磨损进行研究，所以分析中并未考虑渣土改良的影响。

成都地铁3号线红红区间选用了面板式土压平衡盾构进行施工。盾构在砂卵石地层掘进时，对其刀盘进行受力分析可知，刀盘总扭矩主要由刀盘正面摩擦扭矩T1、刀盘背面摩擦扭矩T2、刀盘侧面摩擦扭矩T3、刀盘切削扭矩T4、刀盘搅拌扭矩T5和机械阻力扭矩T6组成。江华等[11]选取北京砂卵石地层4个标段作为实例，得出摩擦扭矩是控制刀盘扭矩的主要因素。李潮等[12]的结论： 相同直径下盾构在非黏性土中需要装载更大的扭矩用于克服刀盘各面摩擦阻力。在实际施工中发现，砂卵石地层中滚刀、刮刀并不直接切削破除卵石，刮刀的主要作用是剥落搅拌地层，滚刀则松动原状地层。同时经现场观测，刀盘损坏形式主要为刀盘周边严重磨损、外边缘刀具刀体严重磨损或脱落。砂卵石地层中刀盘刀具磨损主要是因为地层与刀具间挤压摩擦严重，切削扭矩是存在的，但并不是引起扭矩变化的根本原因。因此，根据已有研究、现场观测及砂卵石地层特性，研究刀具磨损，分析刀盘扭矩参数时，应着重掌握刀盘摩擦扭矩的影响。

3刀盘摩擦扭矩计算模型及其验证

吕强等[13]、邓立莹等[14]提出的摩擦扭矩计算模型中，作用于刀盘上的土压力按均质土层取值，而在实际工程中多为复杂地层，经常遇到盾构掌子面为复合土层的情况。本节建立的摩擦扭矩计算模型充分考虑了多层覆土及复合型掌子面情况，使模型更符合并适用于工程实际。

3.1刀盘正面摩擦扭矩T1

盾构掘进、刀盘旋转过程中，刀盘正面与土体间会发生摩擦，产生摩擦扭矩。当掌子面为单一土层时，其计算模型如图1所示。在刀盘上取一微元进行分析，则有

(1)

式中：γi(i=1，2,…,n)为土体重力密度，N/m3；Hi(i=1，2,…,n-1)为各土层厚度；Hn为第n层土界面距盾构轴线距离；Kn为第n层土体的侧压力系数；D为刀盘直径；f为土与钢的摩擦因数。

对于面板式刀盘，实际计算扭矩时要去掉开口部分的面积。则式(1)可修正为

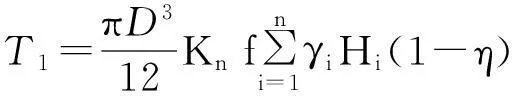
(2)

式中η为刀盘开口率。

如果掌子面为复合型掌子面，这里假设为2种土层，其计算模型如图2所示，计算原理与单一掌子面相同，对第1层、第2层土分别积分，并考虑刀盘开口率的影响，则：

(3)

其中：

(4)

(5)

式(3)—(5)中：σ1v为掌子面第1层土体垂直土压强度；σ2v为掌子面第2层土体垂直土压强度；R为刀盘半径；Kn-1、Kn为相应土层的侧压力系数；f为土与钢的摩擦因数；γi为土体重力密度，N/m3。

图1　单一型掌子面刀盘正面受力模型

Fig. 1Model of force on the front of cutterhead when shield boring in single-component stratum

图2　复合型掌子面刀盘正面受力模型

Fig. 2Model of force on the front of cutterhead when shield boring in complex stratum

3.2刀盘背面摩擦扭矩T2

刀盘背面的摩擦扭矩是否可忽略一直存在争议，卢浩等[15]对该问题进行了详细探讨，证明了刀盘背面的摩擦扭矩是不能忽略的因素。即盾构掘进时，刀盘背面与土仓内的渣土也存在相互摩擦。

T2=kbT1。

(6)

式中kb为与刀盘正面相比刀盘背面摩擦阻力扭矩计算的调节系数，一般取0.6～0.8。

3.3刀盘侧面摩擦扭矩T3

当刀盘外沿超出切口环时，在刀盘转动切削土体的过程中，其侧面与土体发生摩擦，产生刀盘侧面摩擦扭矩。作用于刀盘侧面上的正压力由垂直土压力和侧向土压力组成。为了计算刀盘圆周面的摩擦扭矩，将刀盘侧面的垂直土压力和水平土压力在刀盘圆周面各点分解为垂直于圆周面的正压力，进而求得摩擦阻力。掌子面为单一土层时，刀盘圆周表面受力分析如图3所示。

图3　单一型掌子面作用于刀盘侧面的土压力

Fig. 3Force on side of cutterhead induced by single-component stratum

在图3的圆周侧面上取微面ds进行分析，则作用于ds上的侧向土压力

(7)

作用于ds上的垂直土压力

(8)

将上述2类土压力分解为垂直于侧面的正压力

(9)

(10)

作用在刀盘侧面所产生的摩擦扭矩

(11)

式中W为刀盘圆周侧面宽度。

当掌子面为复合型土层时，刀盘侧面摩擦扭矩计算模型如图4所示，计算公式如下：

(12)

其中：

(13)

(14)

(15)

(16)

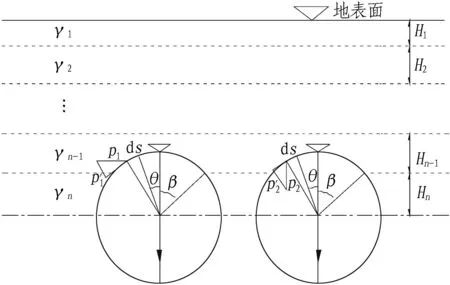
图4　复合型掌子面作用于刀盘侧面的土压力

3.4摩擦扭矩总值Tf

由上述分析可知，刀盘摩擦扭矩总值

Tf=T1+T2+T3。

(17)

3.5摩擦扭矩计算模型的验证

按照推导得出的刀盘摩擦扭矩计算公式，以成都地铁3号线红红区间实际工程为例进行验算，选取第704—742环进行分析。图5为红红区间左线隧道704—742环地质断面详图，表1为盾构的主要相关参数。计算公式中，将计算点选在工程勘探时的钻点，Hi根据断面图计算得出，γi取值参照红红区间岩土工程详勘，刀盘背面摩擦扭矩计算的调节系数kb取0.8，其他参数取值见表1。

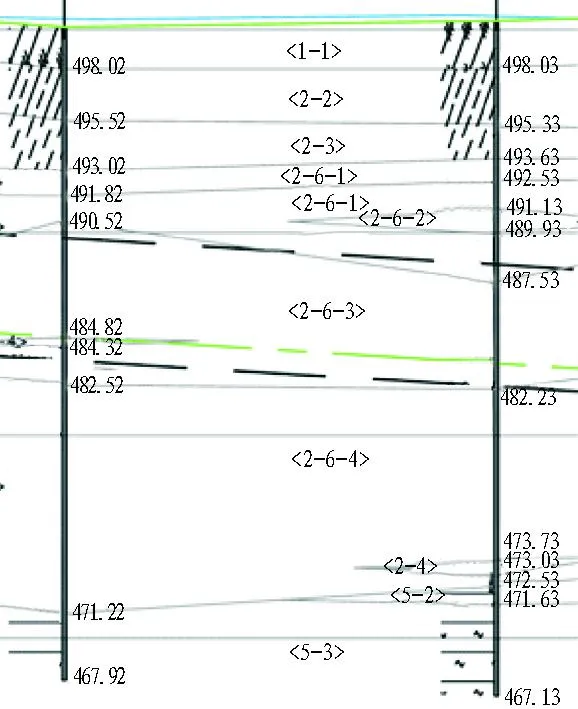
图5　704—742环地质断面详图

Fig. 5Longitudinal profile showing geological conditions of tunnel

表1　盾构及地质参数

(18)

结果表明，砂卵石地层中摩擦扭矩为总扭矩的主要组成部分，这与江华等[11]、李潮等[12]的结论相吻合，也验证了本文中刀盘摩擦扭矩估算模型的正确性。

4运用扭矩参数判断刀具磨损程度

目前，红红区间左线已完工。对该路线施工中换刀点前后刀盘扭矩变化进行统计，如图6所示，对扭矩值取数据库中扭矩最大值进行分析。

图6　扭矩最大值随环号变化曲线

由图6可以看出，随着盾构的掘进，扭矩值在换刀前并未呈增大趋势，换刀点后扭矩降低趋势也不明显，即从图中无法预示刀具磨损，环号增加，扭矩变化较平缓，刀具磨损无明显征兆。

盾构穿越地层时纵向不均匀，有软有硬，变化频次多，同一断面也多为复合地层，因此刀盘扭矩会出现比较大的波动，即地质条件对扭矩有很大影响。由于在砂卵石地层中扭矩主要用于克服刀盘各面摩擦阻力，盾构掘进断面砂卵石磨蚀性越高，刀盘与地层的摩擦阻力就越大，也越容易引起刀具磨损。从摩擦扭矩计算模型可以看出，Tf与地层参数密切相关。因此，在进行刀具磨损分析时，根据地质条件将摩擦扭矩进行分段计算。将摩擦扭矩除以总扭矩得到摩擦比例系数Q，即Q=Tf/T，运用比例系数Q对盾构换刀情况进行分析。统计比例系数Q随环号变化情况见图7。

图7　摩擦比例系数Q随环号变化曲线

比较图6和图7可以看出，比例系数Q波动明显。摩擦比例系数Q换刀前有突变，表明此处刀盘与地层摩擦很大，更易造成刀具磨损，这与实际施工经验一致。表明采用Q值较T值可更好地对刀具磨损做定性预测，与换刀形态具有较好的对应性。工程施工中可运用Q值对刀具磨损、换刀时机进行辅助决策。

5结论与讨论

文章基于刀盘摩擦扭矩参数对刀具磨损问题进行了探讨，取得了一定的成果： 1)建立了充分考虑复合土层情况的刀盘摩擦扭矩计算模型，应用实例验证了其正确性； 2)指出成都地铁砂卵石地层盾构施工中刀盘摩擦扭矩是总扭矩的主要组成部分； 3)分析得出比例系数Q与换刀形态具有较好的对应性，可对刀具磨损进行定性预测，指导工程实践。研究成果可为成都地铁盾构施工中刀具磨损预测提供参考。

由于砂卵石地层的复杂性，盾构施工参数受很多因素影响，各参数关系会相互耦合。本文初步考虑单一因素扭矩与换刀形态的对应关系，得出的比例系数只能定性判断刀具损坏问题。因此，需要探索更加完善的刀具磨损预测模型，进一步提高预测方法的工程应用价值。

参考文献(References)：

[1]张厚美. 盾构盘形滚刀损坏机理的力学分析与应用[J]. 现代隧道技术，2011，48(1)： 61-65.(ZHANG Houmei. Mechanical analysis of TBM disc cutter damage mechanism and its application[J]. Modern Tunnelling Technology, 2011，48(1)： 61-65.(in Chinese))

[2]张厚美. 复合地层中盾构刀具磨损的检测方法研究[C]// 2005上海国际隧道工程研讨会文集. 上海： 同济大学出版社，2005.(ZHANG Houmei. Study on detection method for abrasion of shield cutters in mixed ground[C]// Proceedings of 2005 Shanghai International Symposium of Tunnel Engineering.Shanghai: Tongji University Press, 2005.(in Chinese))

[3]张厚美，区希，易觉. 运用盾构掘进参数跟踪判断滚刀损坏的研究[J]. 现代隧道技术，2014，51(4)：121-126. (ZHANG Houmei, QU Xi, YI Jue. Tracking and determination of cutter damage based on the driving parameters of a shield[J]. Modern Tunnelling Technology, 2014，51(4)： 121-126.(in Chinese))

[4]杨延栋，陈馈，李凤远，等. 盘形滚刀磨损预测模型[J].煤炭学报，2015，40(6)： 1290-1296. (YANG Yandong, CHEN Kui, LI Fengyuan, et al. Wear prediction model of disc cutter [J]. Journal of China Coal Society，2015，40(6)： 1290-1296.(in Chinese))

[5]裴瑞英. 盾构机刀具磨损与布局问题分析研究[D]. 天津： 天津大学，2009. (PEI Ruiying. The analysis and research of cutter wear and its layout for shield machine [D].Tianjin: Tianjin University, 2009.(in Chinese))

[6]刘春花. 砂卵石地层盾构刀盘刀具切削仿真分析[D]. 大连：大连交通大学，2014.(LIU Chunhua. Simulation analysis of cutterhead and cutter cutting of shield machine in sandy cobble stratum[D]. Dalian: Dalian Jiaotong University,2014. (in Chinese))

[7]徐前卫，朱合华，丁文其，等. 均质地层中土压平衡盾构施工刀盘切削扭矩分析[J]. 岩土工程学报，2010，32(1)： 47-54.(XU Qianwei, ZHU Hehua, DING Wenqi, et al. Cutting torque during tunneling process of earth pressure balance shield machine in homogeneous ground[J]. Chinese Journal of Geotechnical Engineering, 2010，32(1)： 47-54.(in Chinese))

[8]王洪新. 土压平衡盾构刀盘扭矩计算及其与盾构施工参数关系研究[J]. 土木工程学报,2009，42(9)： 109-113.(WANG Hongxin. Calculation of cutterhead torque for EPB shield and the relationship between cutterhead torque and shield driving parameters[J]. Chinese Civil Engineering Journal,2009，42(9)： 109-113.(in Chinese))

[9]管会生，高波. 盾构刀盘扭矩估算的理论模型[J].西南交通大学学报，2008，43(2)： 213-217.(GUAN Huisheng, GAO Bo. Theoretical model for estimation of cutter head torque in shield tunneling [J]. Journal of Southwest Jiaotong University, 2008，43(2)： 213-217.(in Chinese))

[10]邢彤，龚国芳，杨华勇.盾构刀盘驱动扭矩计算模型及实验研究[J]. 浙江大学学报(工学版)，2009，43(10)： 1794-1800.(XING Tong, GONG Guofang, YANG Huayong. Torque calculation model of cutting head in shield machine and experimental study[J]. Journal of Zhejiang University(Engineering Science)，2009，43(10)： 1794-1800.(in Chinese))

[11]江华，江玉生，张晋勋，等.北京地铁砂卵石地层土压平衡盾构施工刀盘扭矩研究[J].中国铁道科学，2013，34(3)： 59-65.(JIANG Hua, JIANG Yusheng, ZHANG Jinxun, et al. Research on cutterhead torque during earth pressure balance shield tunneling in sand gravel strata of Beijing Metro[J]. China Railway Science, 2013，34(3)： 59-65.(in Chinese))

[12]李潮，周宏伟，左建平，等.土压平衡盾构刀盘扭矩计算方法与多因素量化分析[J].岩石力学与工程学报，2013，32(4)： 760-765. (LI Chao, ZHOU Hongwei, ZUO Jianping, et al. Torque calculation method of cutterhead in earth pressure balance shield and quantitative analysis of several influencing factors[J].Chinese Journal of Rock Mechanics and Engineering, 2013，32(4)： 760-765.(in Chinese))

[13]吕强，傅德明. 土压平衡盾构掘进机刀盘扭矩模拟试验研究[J].岩石力学与工程学报，2006，25(增刊1)： 3137-3143.(LYU Qiang, FU Deming. Research on torque of cutterhead for earth pressure balance shield with simulating experiment[J]. Chinese Journal of Rock Mechanics and Engineering, 2006，25(S1)： 3137-3143.(in Chinese))

[14]邓立莹，刘春光，党军锋. 盾构机刀盘扭矩及盾体推力计算方法研究[J].矿山机械，2010，38(17)： 13-16.(DENG Liying, LIU Chunguang, DANG Junfeng. Research on method of calculating torque of cutter head of shield machine and thrust of shield [J]. Mining & Processing Equipment，2010，38(17)： 13-16.(in Chinese))

[15]卢浩，王明洋，夏沅谱，等. 土压平衡盾构刀盘扭矩计算模型[J]. 浙江大学学报(工学版)，2014，48(9)： 1640-1645.(LU Hao, WANG Mingyang, XIA Yuanpu, et al. Calculation model of cutterhead torque for earth pressure balance shield[J]. Journal of Zhejiang University(Engineering Science)，2014，48(9)： 1640-1645.(in Chinese))

State Recognition of Cutter Wear Based on Frictional Torque Parameters of Cutterhead

ZUO Cuifeng, TANG Degao, RONG Xiaoli， LIAO Bin

(StateKeyLaboratoryofDisasterPreventionandMitigationofExplosionandImpact,

PLAUniversityofScienceandTechnology,Nanjing210007,Jiangsu,China)

Abstract:The serious shield cutter wear is the key to shield boring in sandy-cobble stratum. In this paper, the composition of shield cutter torque is analyzed in terms of the working principle of earth pressure balance(EPB) shield and the mechanical properties of sandy-cobble stratum. A calculation model of the friction torque is established by means of mathematical and mechanical analysis. The calculation model is verified on the basis of risk monitoring system of shield tunneling; and the cutter wear degree is tracked and recognized by means of proportionality coefficient, combining with the South Hongpailou Station-Hongpailou Station on Line No. 3 of Chengdu Metro as an example. The study results show that: 1) The frictional torques on the front of cutterhead, that on the backside of cutterhead and that on the side of cutterhead are the main components of torque of cutterhead when shield boring in sandy-cobble stratum. 2) The frictional torque model is coincide with the actual construction state. 3) The frictional torque obtained is coincide with the cutter replacing pattern, and can be considered as the recognition reference of cutter wear degree.

Keywords:sandy-cobble stratum; earth pressure balance shield; cutter wear; frictional torque; proportionality coefficient

中图分类号：U 455.3

文献标志码：A

文章编号：1672-741X(2016)03-0344-05

DOI:10.3973/j.issn.1672-741X.2016.03.016

作者简介：第一 左翠凤(1991—)，女，江苏盐城人，解放军理工大学结构工程专业在读硕士，研究方向为地下工程安全风险管理。E-mail: windyzuo1991@163.com。

收稿日期：2015-10-14; 修回日期: 2015-12-18