导流板对海底管线涡激振动的影响

赵恩金，拾兵，曹坤

(中国海洋大学 工程学院，山东 青岛 266100)



导流板对海底管线涡激振动的影响

赵恩金，拾兵，曹坤

(中国海洋大学 工程学院，山东 青岛 266100)

摘要：为了分析在海床冲刷形成浅沟后，自埋现象发生前，海底管线处于悬空状态时，竖向导流板对海底管线涡激振动的影响，在此，通过ANASYS软件对不同导流板高度下，管线周围的流场、压力场等进行了数值模拟分析，得出如下结论：安装导流板后，管线受到的升力系数均值小于0，随着导流板高度与管径之比(h/D)的增加，升力系数幅值不断下降，在高度比h/D为0.375时，基本达到最小值，管线受力总体向下，有利于管线的下沉自埋。在导流板高度与管径比(h/D)为0.25时，发生了涡激振动中的“准周期拍击现象”。拖曳力随着导流板的增大而增加，管线受到的横向作用力增加，其对管线的强度要求增加。

关键词：涡激振动；高度比；升力系数；拖曳力系数；雷诺数；导流板；海底管线

海底油气输送管道是海上油气开发中油气传输的主要方式，是海洋油气生产系统中一个不可缺少的重要组成部分。海底管道经常因水动力因素或者人为因素而遭到破坏，因此管道铺设中经常把管道埋入海床一定深度。埋设后管道在强烈的外界条件下会因局部冲刷而产生裸露和悬空能使裸露在海床的海底管道不能完全自埋。因此国外很早就提出在管道顶部安装导流板以改变水流在管道周边的流态，加速管道底部海床的冲刷，提高管道自埋效果[1]。

Hulsbergen等[2-3]对添加导流板后的冲刷效果进行了试验研究，表明添加导流板后不但可以增加冲刷的深度和宽度，而且还可以加速冲刷过程，添加导流板的管道比没有导流板的管道冲刷速度要快10倍。Chiew[4]通过试验研究了单向流和波浪作用下，管道上安装导流板后对冲刷的影响。Cheng等[5-6]利用数值模拟手段对管道顶部添加导流板后的流场及水动力影响进行了研究，但均没有进行对比试验。任兴月等[7-8]对动床情况下导流板对海底管线的防护功能进行了试验研究。杨兵等[9-10]对近壁面水平圆柱的流向振动进行了研究。李玉成等[11]通过模型试验研究了波浪作用下海底管线受到的升力、拖曳力，他们通过实验分析波浪场中管线周围的流场特性及其对管线受力的影响，为近海管线设计提供了必要的依据。

然而，在带有导流板的海底管线冲刷过程中，极易形成沟而使管线处于悬空状态，此时海底管线在一定的流速下，发生涡激振动，导致管线周围流场和压力场发生变化，对管线本身的受力产生较大的影响，同时对管线的自埋也有一定的影响。本文采用原型管线进行验证，然后选取了不同高度的导流板进行分析和对比，得出相对应的流场分布，压力场分布，拖曳力系数，升力系数等，给出了安装导流板的振动响应对管线自埋的影响程度。

1数值计算

1.1小尺度结构的波流载荷理论

海底管线的流体动力载荷问题十分复杂，在其直径远小于入射波波长时，可以认为构件的存在只在其附近流场引起局部扰动，对波浪绕射作用不明显，采用Morison公式计算水流水平力Fh、垂直的升力Fl：

(1)

(2)

式中：Cd为拖曳力系数；Cm为质量系数；Cl为升力系数；ρ为流体密度，kg/m3；D为管道直径，m；u为来流流速，m/s；∂u/∂t为来流加速度，m/s2。

通过已有的研究可知，拖曳力系数和质量系数随管件振幅变化，前者一般在0.6～1.4变化[12]；升力系数一般在0.25～2.50变化[13]。同时，Reynolds数的计算公式如下:

(3)

式中：μ为流体的粘度，Pa·s；Re为雷诺数，其范围在150～1.5×105时会产生涡街脱落的情况；脱落时，管后交替脱落的漩涡频率[13]为

(4)

式中:f为涡街脱落频率,Hz。f、U、D可组成一无因次系数，用Strouhal数St表示。根据罗斯柯(Roshko A)1955年的实验[14]，在Re=150～1.5×105范围内,St数近似等于常数0.21。

1.2数值建模

安装导流板的海底管线如图1所示。

图1　导流板布置图Fig. 1　Sketch of submarine pipeline with spoiler

利用ANSYS-CFD软件建立3D流场网格分析模型，如图2所示。取30D×20D×5D(D为管线圆柱的直径，D取0.01 m)的空间为计算区域，其中管线在顺流方向上游10D，下游20D，管线上下均为10D的位置处，管线轴线方向取5D。海流入口边界，给定速度值,u=0.02 m/s，v=w=0，压强值p=0；出口边界，沿流线方向各流动参数的导数为零，给定压力和压力梯度P=∂p/∂i=0；i代表3个不同方向，计算区域的上下面均采用滑动墙面设定，壁面剪应力为0，壁面附近的流体速度并不受壁摩擦的影响。左右边界采用对称壁面边界；圆柱壁面采用接触条件。以入口边界条件作为计算的初始条件。

图2　流场网格分析模型图Fig. 2　Fluid mesh analysis model diagram

采用四种不同尺度的导流板，高度用h表示，其高度与管线直径之比(h/D)分别为0.125、0.25、0.375、0.5。如果h/D继续升高的话，导流板上产生的力对管线造成的扭矩对管线的影响占主导地位。模拟工况如表1所示。

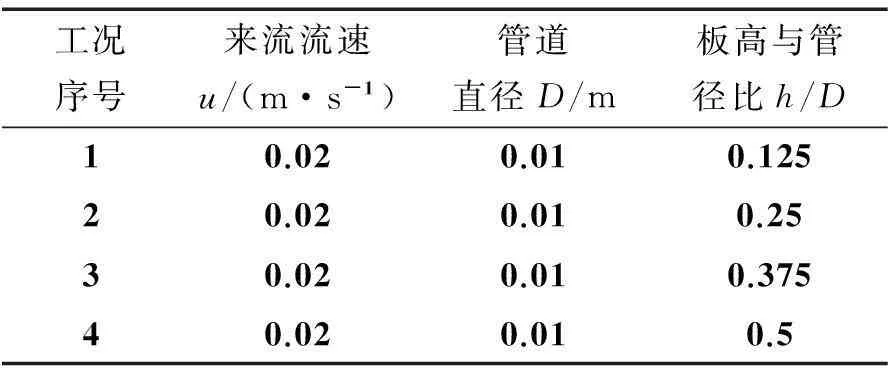
表1　模拟工况

2固定圆柱体绕流分析

为了保证在安装导流板之后，流固耦合模拟的准确性，并且能够和原型管线进行对比，先进行圆柱扰流分析。得出Re=200时固定圆柱绕流升阻力曲线，如图3所示。从图3中可以看出，阻力系数Cd随着时间增加逐渐增大并稳定在1.30左右，升力系数Cl幅值稳定在0.7左右。通过与经典结果[15-19](表2)对比可知，圆柱绕流时有足够的精度，确保了后面流固耦合计算时CFD模拟的精确性。

图3　Re=200时升阻力系数Fig. 3　 Cl and Cd under Re =200

Re=200Cd均值Cl均值St文献[15]1.310.650.19文献[16]1.290.600.19文献[17]1.300.700.19文献[18]1.20N/A0.19文献[19]1.290.740.18本文结果1.300.700.193

3不同高度比导流板数值模拟分析

3.1流场图分析

首先对产生涡激振动的导流板管线周围的流场分析，得出不同高度比的流场云图，如图4所示。

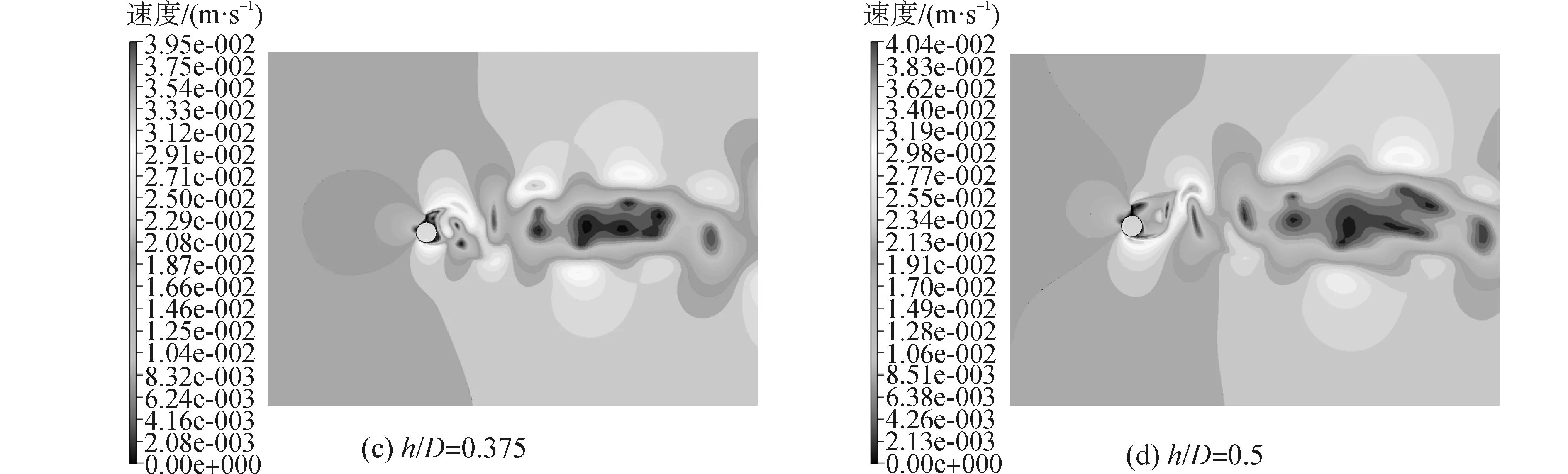
图4　不同导流板高度下管线周围的流场图Fig. 4　Flow fields around submarine pipeline with different height spoilers

通过流场图可以发现，管线上方涡旋的脱落主要集中在导流板的后方，而不存在导流板时，涡旋主要在管线的后方。随着导流板的增高，涡旋的形态发生了变化，由比较规则的对称涡旋向不规则的涡旋过渡，在一定程度上避免了“锁定”现象的发生，管线下方分离点前移，加速了管线下方泥沙的冲刷，对管线的下沉自埋有一定的帮助。当h/D为0.5时，涡激振动现象表现出了上下涡旋脱离管线之后在尾流会合的现象，对管线横向作用力明显加大。

3.2压力场图分析

对导流板管线周围的压力场进行分析，得出了导流板在不同高度比时的压力场云图，如图5所示。

未添加导流板的管线，当流体接近物体前缘时，因受阻碍而压力增大，在管线中心前端壁面处压力最大，流速为零，此点为前驻点，即图1所示180°的位置。通过图5可见，由于竖向导流板的存在使前驻点，即压力最大，流速为零的点上移，在90°～180°位置之间，在此范围内表面压力增大，导流板上的压力同时增加，减小了直接作用在海底管线上的拖曳力。随着导流板的增高，对周围压力场的影响也增大。

图5　不同导流板高度下管线周围的压力场图Fig. 5　Pressure fileds around submarine pipeline with different height spoilers

当流体流过装有导流板的海底管线时，边界层外流体速度在管线上方导流板的顶端和管线下方分离点处发生改变，在导流板顶端点之前区域中沿流动方向速度渐减而压力渐增，顶端点之后沿流动方向速度递增而压力减小，在管线下方分离点前后遵循同样的规律。由于边界层很薄，边界层的压力可认为等于边界层上的流体压力，所以沿圆柱体表面的边界层中，也具有和边界层外流体相同的压力分布规律。因此，流体过了导流板顶端点以后，边界层内流体质点除了受摩擦阻力作用外，还受与流动方向相反的压力差的作用，由于竖向导流板的形状为竖直面，相对于圆形面而言提供的运动方向的力要小的多，因此，存在导流板造成的压力差远远大于圆形截面的压力差，而使流体迅速进入回流状态，在管线上方形成的涡旋主要集中在了导流板的后面，导流板越高后方产生的涡旋越大，同时，管线受到的作用力也渐渐向导流板上过渡，减少了直接作用在管线上的力。

随着导流板的增加，涡激振动产生的交替的压力分布不再表现出规则的对称性，横向水平对称轴逆时针旋转在270°～360°。管线总体受到的水平力的方向为来流方向，垂向受力在一个周期内负的升力渐渐大于正的升力，总体受力有利于管线的下沉。

3.3拖曳力系数及升力系数分析

在此取具有代表性的导流板高度进行了研究，从图6发现，在大约800 s时间步之前，升阻力系数随时间增加而增大，达到峰值后升阻力系数缓慢的降低，直到一个较稳定的值，这个现象体现了涡激振动的自限性，当管线的振动达到一定程度时，对流场的扰动增强，破坏了涡旋的脱落形态，流场的变化又反过来影响管线的振动，但这个特性不会使升阻力系数一直变动，而是最终稳定在某个范围内[20]。从图14可以看出，h/D=0.5时，在800 s时间步之前，也会存在流固耦合阶段且呈现峰值不稳定的情况，当流固耦合到达稳定阶段，由于导流板的严重影响，升力系数和拖曳力系数的峰值也是时大时小，在图中最终节点2 000 s处，Cl数呈现增大趋势，但会重复之前的过程，取图时为了和前面时间同步，起到对比作用，故到此为止。

通过对不同高度导流板产生的对海底管线拖曳力系数和升力系数的分析可知，随着导流板的增高，拖曳力系数逐渐增加，迎流面积也在增加，对海底管线产生的拖曳力增加，对管线的刚度要求增加，产生的周期频率基本不变，但是由于导流板的存在，管线的形状发生变化，不再是对称结构，在导流板上方产生的力和管线下方产生的力的大小不再相等，拖曳力系数的峰值发生了变化。随着导流板高度的增加，平均升力系数的绝对值不断增加，在h/D为0.375时，升力系数的最大值小于0，说明此刻管线竖直方向的周期力全部是竖直向下的，有利于管线的下沉。

在导流板高度与管径比例(h/D)为0.25时，产生了涡激振动中的“准周期拍击”现象[21]，这是在拖曳力系数低频率的振荡为了与升力系数幅值变化步调调整一致造成的，即卡门涡街中多重频率的漩涡脱落频率叠加引起的。当h/D为0.5时，升力系数和拖曳力系数表现出了明显的不规则性，周期也发生了改变，减少了共振产生的危险性。

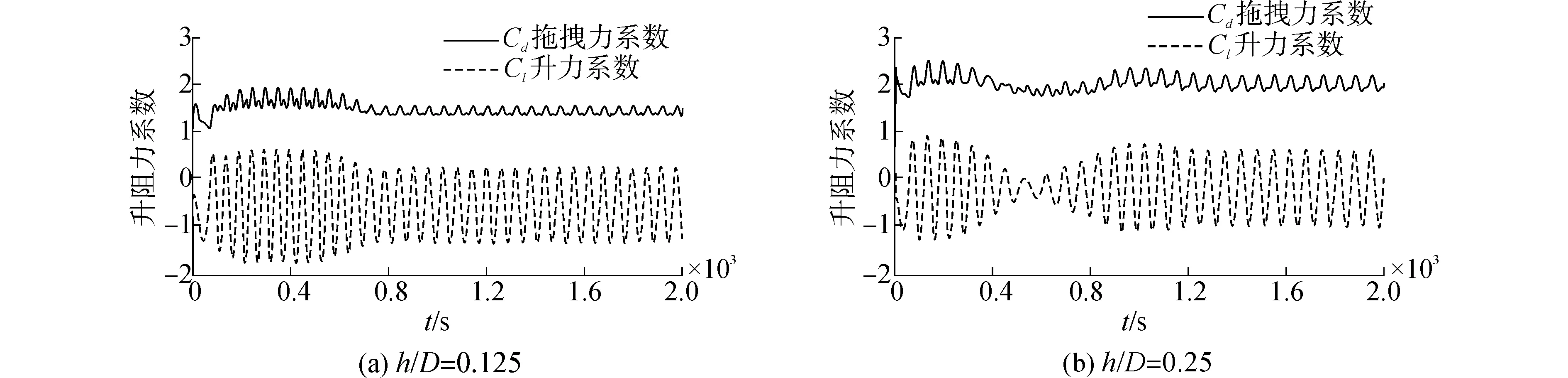
图6　不同导流板高度下的升阻力系数Fig. 6　Cl and Cd under different spoiler heights

通过对升力系数和拖曳力系数整体分析，得出不同高度比的升力系数和拖曳力系数均值，如图7所示。h/D为0.125、0.25、0.375、0.5时，平均拖曳力系数均值为1.549、1.896、2.076、2.080；平均升力系数均值为-0.501、-0.768、-0.828、-0.882。

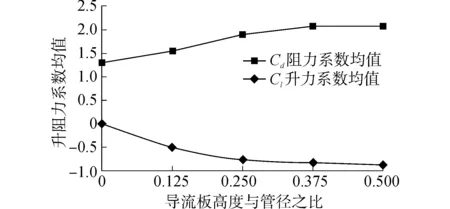
图7　升阻力系数均值随高度比的变化曲线Fig. 7 Cl and Cd various curves under different height ratios

涡激振动中平均阻力系数和平均升力系数随导流板高度的变化而变化，通过图7可知，随着导流板高度的增加平均升力系数不断下降，说明管线受到的竖直方向力的绝对值不断增加；而平均拖曳力系数也不断增大，说明管线受到的水平方向的作用力不断增大。在h/D为0.375和0.5时，对两系数均值进行比较，发现两者的升力系数均值相差不大, 在h/D为0.375时，升力系数均值基本达到最小值，即绝对值达到了最大值。拖曳力系数在h/D为0.5时，该系数的最大值增加，但由于其周期性的值不稳定，而在计算拖曳力系数的均值时并未表现出较大的增加。同时，在h/D为0.5时，增加了迎流方向的面积，使管线受到的拖曳力增加，不利于管线的安全，在此基础上，可以控制高度比h/D为0.375，对管线较有利。在安装导流板时应同时考虑两个方向的受力情况，选取合适的导流板高度与管径的比例。

4结论

本文采用流固耦合方案研究安装不同高度比导流板的海底管线涡激振动特性，得出如下结论：

1)通过数值模拟研究了h/D为0.125、0.25、0.375、0.5时，管线周围流场、压力场、升阻力系数等的变化，并发现了“准周期拍击”的现象。

2)安装导流板后，管线下方的分离点前移，加速了管线下方的冲刷，随着导流板的增高，作用在管线上的竖直方向的周期性作用力逐渐增大，方向也转变成一直竖直向下，在产生涡激振动时，有利于管线的下沉自埋，但是，导流板增高也使拖曳力周期性的增加，提高了对管线的刚度和韧性要求。

3)通过对不同高度比造成的涡激振动升阻力系数的分析可知，当h/D=0.375时，升力系数均值基本达到最小值，而此刻相对较高的导流板而言又是受到拖曳力影响最小的。

本文主要考虑到涡激振动明显的状况，故选取了一种有代表性的流速，让其产生典型的涡激振动的状态。因此，未选取多种流速。今后，对多种流速将做进一步研究。

参考文献：

[1]张芝永, 拾兵, 范菲菲, 等. 导流板对海底管道绕流影响的数值模拟与试验研究[J]. 水动力学研究与进展, 2011, 26(5): 597-605.

ZHANG Zhiyong, SHI Bing, FAN Feifei, et al. Numerical simulation and experimental study on flow around submarine pipeline with spoiler[J]. Chinese journal of hydrodynamics, 2011, 26(5): 597-605.

[2]HULSBERGEN C H. Stimulated self-Burial of submarine pipelines[C]//Proceedings of Offshore Technology Conference. Houston, Texas, 1986: 441-444.

[3]HULSBERGEN C H, BIJKER R. Effect of spoilers on submarine pipeline stability[C]//Proceedings of Offshore Technology Conference. Houston, Texas, 1989: 337-350.

[4]CHIEW Y M. Effect of spoilers on scour at submarine pipelines[J]. Journal of hydraulic engineering, 1992, 118(9): 1311-1317.

[5]CHENG L, CHEW L W. Modelling of flow around a near-bed pipeline with a spoiler[J]. Ocean engineering, 2003, 30(13): 1595-1611.

[6]ZHAO Jianping, WANG Xuechao. CFD numerical simulation of the submarine pipeline with a spoiler[J]. Journal of off-shore mechanics and arctic engineering, 2009, 131(3): 21-27.

[7]任兴月. 海底管线导流技术的数值计算与试验研究[D]. 青岛: 中国海洋大学, 2009: 36-45.

REN Xingyue. Experimental and numerical study on the submarine pipelines with spoiler[D]. Qingdao: Ocean University of China, 2009: 36-45.

[8]韩艳, 拾兵, 任兴月, 等. 导流板对海底管线防护功能的试验研究[J]. 四川大学学报: 工程科学版, 2010, 42(2): 100-106.

HAN Yan, SHI Bing, REN Xingyue, et al. Experimental study on the function of spoilers in protecting submarine pipeline[J]. Journal of Sichuan university： engineering science edition, 2010, 42(2): 100-106.

[9]杨兵, 高福平. 单向流作用下近壁面圆柱的流向振动[J]. 水动力学研究与进展, A辑, 2010, 25(1): 119-125.

YANG Bing, GAO Fuping. Stream-wise vibration of a near-wall cylinder exposed to unidirectional flow[J]. Chinese journal of hydrodynamics, series A, 2010, 25(1): 119-125.

[10]GAO Fuping, LUO Chengcai. Flow-pipe-seepage coupling analysis of spanning initiation of a partially-embedded pipeline[J]. Journal of hydrodynamics, series B, 2010, 22(4): 478-487.

[11]李玉成, 陈兵, 王革. 波浪对海底管线作用的物理模型实验及数值模拟研究[J]. 海洋通报, 1996, 15(4): 58-65.

LI Yucheng, CHEN Bing, WANG Ge. Physical model test and numerical simulation of pipeline under wave action[J]. Marine science bulletin, 1996, 15(4): 58-65.

[12]王贵春. 水流作用下圆柱体的涡激振动分析[J]. 科学技术与工程, 2007, 7(1): 22-25.

WANG Guichun. Analysis of vortex induced vibration of a cylinder in steady flow[J]. Science technology and engineering, 2007, 7(1): 22-25.

[13]CHAKRABARTI S K. The theory and practice of hydrodynamics and vibration[M]. River Edge, NJ, USA: World Scientific, 2002: 150-187.

[14]ROSHKO A. On the wake and drag of bluff bodies[J]. Journal of the aeronautical sciences, 1955, 22(2): 124-132.

[15]BRAZA M, CHASSAING P, MINH H H. Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder[J]. Journal of fluid mechanics 1986, 165: 79-130.

[16]LECOINTE Y, PIQUET J. Flow structure in the wake of an oscillating cylinder[J]. Journal of fluids engineering, 1989, 111(2): 139-148.

[17]SARPKAYA T. A critical review of the intrinsic nature of vortex-induced vibrations[J]. Journal of fluids and structures, 2004, 19(4): 389-447.

[18]ONGOREN A, ROCKWELL D. Flow structure from an oscillating cylinder Part 1. mechanisms of phase shift and recovery in the near wake[J]. Journal of fluid mechanics, 1988, 191: 197-223.

[19]魏志理, 孙德军, 尹协远. 圆柱尾迹流场中横向振荡翼型绕流的数值模拟[J]. 水动力学研究与进展, A辑, 2006, 21(3): 298-308.

WEI Zhili, SUN Dejun, YIN Xieyuan. A numerical simulation of flow around a transversely oscillating hydrofoil in the wake of a circular cylinder[J]. Journal of hydrodynamics, series A, 2006, 21(3): 298-308.

[20]范杰利. 质量比对细长圆柱体涡激振动影响的数值研究[D]. 青岛: 中国海洋大学, 2013: 55-75.

FAN Jieli. Numerical simulation of mass ratio's effect on vortex-induced vibrations of slender circular cylinder[D]. Qingdao: Ocean University of China, 2013: 55-75.

[21]郑婷婷. 螺旋侧板抑制海洋立管涡激振动的机理研究[D]. 镇江: 江苏科技大学, 2013: 23-45.

ZHENG Tingting. Study on mechanism of the influence of spiral side on vortex induced vibration inhibition[D]. Zhenjiang: Jiangsu University of Science and Technology, 2013: 23-45.

Influence of reflectors on vortex-induced vibration of subsea pipelines

ZHAO Enjin, SHI Bing, CAO Kun

(College of Engineering, Ocean University of China, Qingdao 266100, China)

Abstract：In order to analyze the influence of vertical reflectors on the vortex-induced vibration of subsea pipelines after a shallow gully has formed by seabed scouring, before the self-burial phenomenon occurs, and when the subsea pipelines are still suspended, we used ANASYS software to carry out a numerical simulation analysis on the flow and pressure fields surrounding the pipelines at different deflector heights. The following results were obtained: after the installation of the deflector, the average coefficient of the lift force borne by the pipeline was less than zero. With increases in the ratio of the reflector height to the pipe diameter (h/D), the amplitude of the lift coefficient continuously decreased. When the h/D ratio was 0.375, the amplitude of the lift coefficient reached a minimum value, and the force borne by the pipelines was generally downwards, which can help the pipelines to sink and be buried on their own. When the h/D ratio was 0.25, a quasi-periodic slapping phenomenon occurred in the vortex-induced vibration. The drag force increased with the enlargement of the deflector. With an increase of the horizontal force borne by the pipeline, the required strength of the pipeline also increases.

Keywords：Vortex-induced vibration (VIV); ratio of reflector height to pipe diameter; lift coefficient; drag coefficient; Reynolds number; deflector; subsea pipeline

中图分类号：P751

文献标志码：A

文章编号：1006-7043(2016)03-320-06

doi:10.11990/jheu.201411081

作者简介：赵恩金(1986-)，男，博士研究生；拾兵(1961-)，男，教授，博士生导师.通信作者：拾兵，E-mail：bings@ouc.edu.cn.

基金项目：国家自然科学基金资助项目(51279189).

收稿日期：2014-11-26.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160104.1427.008.html

网络出版日期：2016-01-04.