运用环节教学法，激“活”初中数学课堂

吴琼

摘 要：环节教学法是当前初中数学教学领域中出现的新理念，这一理念主张将数学教学过程划分为一个个具体环节，分别落实完成，以实现每个环节的高效运行，从而提升整体教学实效。这一思路为初中数学教师打开了全新的教学视野，作者在实际教学中对这一方法进行了多次实践，效果显著，本文对此进行了简要的总结阐述，希望能对广大初中数学教师们有所启发。

关键词：初中 数学 环节教学

一次完整的初中数学课堂教学可以划分为预习、学习、复习等基本环节。环节的划分使得整个教学过程清晰明了、按部就班，同时，也使得教师可以依据当前学生知识掌握中存在的不足之处，有针对性地对相应环节进行教学设计的调整与完善。这样一来，课堂教学实效可以获得显著提升，数学课堂也能够在一个个环节的巧妙设计中“活”起来。

一、自主学习环节——在预习中发现问题

预习是整个数学课堂教学过程中的第一个环节。然而，预习环节常常得不到教师和学生应有的重视。学生经常跳过预习环节直接进行课堂学习，教师对于学生预习效果的监督与验收力度欠缺，造成很多情况下预习环节“名存实亡”。环节教学法则对预习进行了较为突出的强调。

例如，在初中数学七年级下册第五章第一节的教学内容中，介绍了很多由两条直线相交而出现的角的关系。这些知识点较为琐碎，但难度都不大，如果都放在课堂教学当中逐个罗列讲解，既浪费了有限的课堂教学时间，也会让整个教学过程枯燥乏味。因此，对这部分内容的学习理解比较适合交给学生在预习环节中完成。对于学生预习环节的完成效果，作者主要采取课堂提问的方式进行验收。首先，作者在黑板上画出两条直线AB、CD相交于点O，同时形成四个角。分别将∠AOC标记为∠1，∠BOC标记为∠2，∠BOD标记为∠3，∠AOD标记为∠4。然后，作者要求学生找出该图形中不同位置关系的角，并且使用规范的语言进行表述。学生都能回答出：“∠1与∠3互为对顶角，∠2与∠4互为对顶角，∠1与∠2、∠2与∠3、∠3与∠4、∠1与∠4互为邻补角。”作者根据学生的回答了解到学生对这些角的位置关系的概念掌握得比较到位。随后，作者又要求学生指出这些角之间的大小关系，学生利用“对顶角相等”“邻补角互补”等性质分别做出了正确的判断。通过简单的提问环节，作者就能了解到学生对于这部分知识的预习情况，同时也得以顺利进行接下来的教学内容，大大节约了课堂教学时间。对于不甚复杂的知识，学生是完全可以通过自主学习环节学习掌握的。

预习是十分重要的一个教学环节，不仅可以让学生通过预先学习对知识进行先期接受，使得课堂学习的难度降低，还能够为学生创设一个自主学习的平台，锻炼其独自处理问题的能力。因此，预习环节往往能够达到一举两得的教学效果，不容忽视。

二、合作交流环节——在互动中解决问题

预习过后，便要进入主体学习环节了。这一环节的教学是学生接受、理解知识最为集中的阶段，也一直是教师关注度最高的部分。在课堂教学当中，作者常用的做法是通过小组合作的形式，引导学生对力所能及的问题进行初步的探究。

例如，在初中数学九年级下册第二十七章第二节相似三角形这一部分内容的教学当中，作者就将课堂学习的主动权交给了学生。作者将6～8名学生分为一组，发给每组学生一组相似三角形的模型，不给学生任何提示，要求其通过合作讨论的方式探究出相似三角形所具有的性质。面对互为相似三角形的△ABC与△A′B′C′，学生先是将两个图形变换位置观察，随后通过沟通交流发现，还是以数据来判断最为有效。于是，开始利用直尺和量角器进行测量。通过分别对三角形的三条边进行测量，学生发现，相似三角形三条边的边长满足AB∶A′B′=BC∶B′C′=AC∶A′C′。与此同时，在角度方面还满足∠A=∠A′，∠B=∠B′，∠C=∠C′。相似三角形的性质就这样在学生的合作讨论中被相继发现了。学生如此高效地自主探究出结果，也让作者感到十分意外，作者也及时对大家的灵活思维进行了肯定与鼓励。

由此可见，在小组讨论形式的辅助之下，学生自主解决数学问题的能力还是很强的。在课堂学习环节中，利用小组讨论方式，给学生提供一个相互交流启发的空间，对学生数学学习能力的提升大有益处。

三、精讲点拨环节——在讲解中升华问题

当然，要想掌握初中数学知识仅靠学生的自主学习是远远不够的。对于教材中的重点内容，仍然需要教师的着重点拨与讲解，才能使学生明晰掌握，实现学习效果的飞跃。

例如，在初中数学七年级上册第一章第一节中，学生学习了正数和负数的相关知识。通过观察学生在小组讨论过程中的实际表现，作者发现学生在自主理解正负数的含义时存在两个问题：一是仅仅从数量大小关系上来理解数字的正与负，二是简单地认为，只要数字前面带有“-”，该数字就是一个负数。针对这两个比较严重的概念性问题，作者在课堂教学中进行了重点讲解。首先，作者以存折上的数字为例，“500”代表存入了500元，那么“-500”又代表什么呢？学生反应出是支取了500元的意思。因此可以看出，“-”除了可以表示数字的大小关系以外，还可以表示“相反”的概念。这时再让学生观察等高线的图示，学生便很容易明白“9900”代表高出水平面9900米，而“-990”则表示低于水平面990米。与此同时，对于学生认为只要数字前面带有负号该数字就是负数这一错误概念，作者利用反例向学生进行讲解。在-7.6，-78%这种形式的数字都是负数的基础上判断-a是不是负数呢？当a=-7时，-a=-（-7），它还是负数吗？学生恍然大悟，对于负数的判断要从其实际正负来看，仅从符号上判断是远远不够的。

在课堂教学当中，教师的精讲点拨是整堂课的点睛之笔。要想让精讲点拨能够切中要害，还要求教师对上一个合作交流环节当中学生的探究表现进行细致观察，找到学生存在的知识内容与思想方法上的问题，以便进行有针对性的精讲。

四、有效训练环节——在实践中拓展问题

在预习、学习之后，紧接着的就是复习环节。复习是对所学新知识的回顾与巩固，在重温知识与方法的同时发现新问题，从而在解决这些问题的过程中得到对知识的再认识。因此，课后复习必不可少。

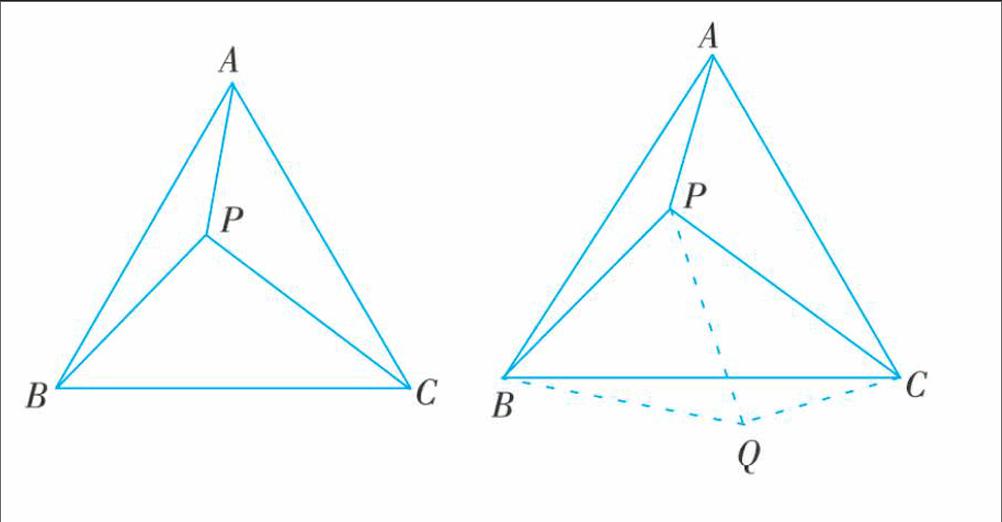
例如，在初中数学九年级上册第二十三章中，学生学习了关于旋转的相关内容。这部分内容看似简单，在实际应用当中却可以非常灵活地命题。在学生掌握了图形旋转与中心对称的基本规则与方法之后，作者利用课后习题的方式对这部分内容的具体应用进行了适度拓展。题目条件很简单：已知，如图（下图左）所示，△ABC是正三角形，P是三角形内一点，PA=3，PB=4，PC=5。求：∠APB的大小。这种命题形式让很多学生顿时没有了思路，不知道该从何处入手，更不知道这和旋转的知识内容有什么联系。针对学生的困惑，作者对这道习题进行了重点讲解。在这道题中，正是由于没有现成的条件，才应该考虑通过旋转的方式，搭建出一些辅助条件。比如可以将△ABP顺时针旋转60°成为△CBQ，连接PQ（下图右）。这样一来，结合旋转与全等三角形的知识，便可以得出△BPQ是正三角形的结论，从而推导出△PQC是直角三角形。接下来就不难求出∠APB=150°了。

课后习题是对数学知识进行有效训练的常用方法。依据不同的训练目标，教师可以选择不同难度与内容的习题供学生练习。在完成习题的过程中，学生不仅能够找到理论学习与问题解决之间的衔接点，还能够通过训练拓宽知识面，提升学习效果。

以上就是作者在教学实践中运用环节教学法进行数学课堂教学的具体做法。在环节教学法中，数学学习中的每一个必要环节都得到了教师与学生的重视。与此同时，通过教师对各个环节的巧妙设计，整个数学课堂被有效激活，学生在每个环节的学习当中都能保持高热情、实现高效率。

参考文献

[1]丁岩.引入生活活水 滋润数学课堂[J].数学学习与研究，2014（12）.

[2]陈冬.数学课堂教学有效性的调控策略[J].现代中小学教育，2008（2）.