处理多介质界面的改进型Front Tracking方法*

童石磊，钟 敏，柏劲松，陈森华

(中国工程物理研究院流体物理研究所，四川绵阳 621999)

1 引 言

多介质界面的数值模拟和界面运动追踪是近年来计算流体力学研究的热点问题，在材料科学、天体物理以及核物理等领域也有着广泛应用。目前，处理多介质界面的数值模拟方法有Level-Set方法[1]、VOF方法[2]和Front Tracking (FT)方法[3]等。其中，FT方法是由James Glimm等人于20世纪80年代提出的，主要思想是通过参数表示的闭合曲线表征界面位置，界面随着表征曲线的运动而运动。一般而言，这组闭合曲线由一些标记点(示踪点)组成，通过记录示踪点的运动即可捕捉到界面的运动情况。FT方法的优点在于能准确地捕捉界面的位置，使用了准确的间断条件，不引入数值扩散，避免原本锐利的界面变得平滑；缺点在于算法比较复杂，难以处理拓扑结构变化，难以向高维推广。Glimm及其团队对FT方法做了许多研究工作，取得了不少有价值的成果[4]，例如二维和三维的复杂数据存储和处理方法、界面拓扑混乱的避免和纠正方法等。为避免和纠正拓扑混乱，Glimm等人[5]采用了Grid Free (GF)、Grid Based (GB)、GF和GB混杂以及Local Grid Based (LGB)等方法。GF方法的主要特点是不依赖辅助坐标系即可删除产生界面拓扑错误的部分，重新调整网格分布和尺寸；GB方法则是引进辅助坐标系来完成这项任务。GF方法的数值扩散较小，调整后的三角形元素形状和尺寸好，计算精度高，但是不能处理拓扑性质复杂的问题；而GB方法的数值扩散大，生成的三角形元素质量差，但是可以改善对复杂拓扑问题的处理效果。混杂方法是周期性地交替使用GF和GB方法，平衡了两种方法的优缺点。LGB方法则是限制GB方法的使用范围。

处理界面拓扑性质复杂的问题时，FT方法出现困难的主要原因在于缺少对边界处理的方法。本研究在经典FT基础上，将边界上的拓扑结构变化通过示踪点组成的线段进行描述，边界运动情况通过示踪点线段的添加、合并、删减自然地表达，产生的新界面则由新的示踪点线段组成。通过这些改进建立一种能够有效处理界面拓扑变化的方法，以期为处理复杂界面问题提供参考。

2 数值分析与数据结构

对于FT方法，界面函数f上的示踪点坐标满足

(1)

界面发展规律可以通过求解(2)式确定

(2)

式中：x为示踪点位移，x0为示踪点的初始位置，v为示踪点的速度，t为时间。

2.1 传统FT方法

传统FT方法将示踪点依次编号，并按编号顺序将示踪点相连组成封闭界面。对于二维问题，通常以二维数组Tx(N,L)和Ty(N,L)表示示踪点坐标，N为材料号，L为示踪点编号。图1为传统FT方法示踪点的分布，其中数字为不同的示踪点编号，A物质位于示踪点走向的左侧。

处理多物质界面相交的问题时，传统FT方法很容易在交界面处产生拓扑混乱。如图2所示，曲线界面走向的左侧为A物质，直线界面走向的左侧为B物质，1、2、3、4、5为曲线界面上示踪点。采用传统FT方法计算时，由于无法保证界面相交之前恰好处于刚刚接触状态，因此，在下一个计算时间内，很可能出现界面直接嵌入的情况(如图2中虚线所示，示踪点3、4、5走向的左侧既含有A物质，也含有B物质)，从而导致拓扑混乱，使计算无法继续进行。拓扑混乱的出现限制了传统FT方法的应用，针对该问题，Glimm等人对传统FT方法进行了改进，使其能够处理界面拓扑结构的变化，但是该方法仍然存在很大的局限性，并且要求问题中不能超过3种物质。此外，为处理界面拓扑结构变化，在界面接触之前，需要对界面示踪点进行一次重新分布，界面相交后，每运行一个时间步，就需要对示踪点进行一次重新分布，计算过程十分繁琐，精度也不高。

图1 传统FT方法示踪点分布Fig.1 Distribution of tracer points in classic FT method

图2 拓扑混乱情况Fig.2 Topological chaos

2.2 改进的FT方法

如图3所示，改进的FT方法用示踪点线段描述界面，采用数组T(s,e,ml,mr)表示示踪点线段，并对线段进行编号，s表示线段的起点坐标，e表示线段的终点坐标，ml表示线段左侧物质的编号，mr表示线段右侧物质的编号。当不同编号的线段具有相同的端点坐标时，认为线段相连，并由相连线段组成封闭界面。改进的FT方法通过数组T即可清楚描述界面相关量，因此线段编号可以任意给定。

针对界面相交时拓扑混乱产生的问题，在已求得界面传播速度的条件下，改进的FT方法通过设定界面Ⅰ上示踪点到达界面Ⅱ的最短时间，来保证界面结构发生拓扑变化前恰好处于接触状态，具体方法如下：首先，通过数组T确定初始时刻的界面位置，再利用界面传播速度求得界面Ⅰ上的示踪点到达界面Ⅱ位置所需的时间，选取其中最短的时间作为界面相交的判定条件，即可保证拓扑变化前界面处于恰好相接触的状态，避免拓扑混乱的产生。

图3 改进FT方法示踪点线段的分布Fig.3 Distribution of segments using improved FT method

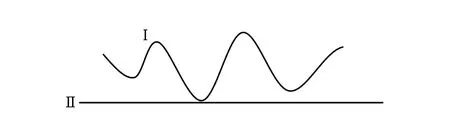
图4 界面恰好接触Fig.4 Interface just in contact

改进的FT方法对界面拓扑结构变化的处理主要通过示踪点线段实现。以两界面相交问题为例，改进的FT方法对界面拓扑结构变化问题的处理如图5所示，其中共包含3种物质，编号分别为0、1、2。选取部分界面进行考察，设定最小距离d，当示踪点间距离小于d时，认为示踪点重合为一点；当示踪点与示踪点线段间距离小于d时，认为示踪点与线段融合，并将线段分成两部分。图5(a)中，示踪点线段A1B1与A2B2两侧的物质不同，当两示踪点线段相互接近至距离小于d时，线段融合产生新的界面A0B0；图5(b)中，线段A1B1与A2B2发生融合后，得到的新线段两侧均为物质1，因此新线段可以直接消去，完成界面拓扑结构的变化。

改进的FT方法处理界面拓扑结构变化问题的计算流程如图6所示。通过以上分析可以发现，改进FT方法采用示踪点线段对界面进行处理十分简便，由此我们可以建立新的界面拓扑结构变化追踪和模拟机制，并进行计算程序编写。

图5 界面拓扑结构变化Fig.5 Topological changes of interface

图6 改进的FT方法处理界面拓扑结构问题流程图Fig.6 Flowchart of the improved FT method

3 数值算例

采取二维算例检验改进FT方法的可靠性，以下物理量均为无量纲量。算例采用一阶格式进行离散并设定误差允许区间，计算结果满足精度要求，在以后的应用中可以采用更高阶离散格式得到更高精度的结果。由于两算例在界面变化过程中均没有进行质量输运，因此满足质量守恒。

3.1 圆柱贯穿靶

本算例主要用于验证改进的FT方法能否有效处理界面拓扑的变化。图7为圆柱物质A贯穿矩形靶板物质B的过程，其中物质A为刚体，物质B为无强度、质量为零的理想可变形体。该模型的特点是排除了状态方程、本构关系等真实物理参数的测量误差对计算结果的影响。C物质为真空，计算区域为[-200,200]×[-150,300]，计算时间为72，速度条件为

(3)

对贯穿过程进行分析可以发现，界面拓扑变化分为以下4个过程。初始状态下，界面如图7(a)所示，A物质与B物质相互独立，有各自的边界；当t=24时，界面位置如图7(b)所示，A物质穿入B物质，两物质之间有一条公共边界，拓扑性质发生第1次变化；当t=48时，界面位置如图7(c)所示，A物质开始部分穿出B物质，B物质被分为两部分，原来的公共边界消失并产生了两条新的公共边界，拓扑性质发生第2次变化；当t=72时，界面位置如图7(d)所示，A物质完全穿出B物质，公共边界消失，B物质被分解为两个完全独立的部分，拓扑性质发生第3次变化，计算终止。

由图7圆柱贯穿靶过程中界面的变形情况可以看出，改进的FT方法在处理界面拓扑结构变化时继承了传统方法的优点，物质界面运动情况能够得到清晰的追踪，界面形状得到了较好的保持，同时保证了界面尖锐部分不会变得圆滑。

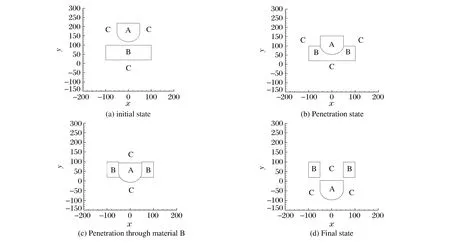
图7 圆柱贯穿靶过程中的界面变形情况Fig.7 Deformation of cylinder-target interface in penetration process

3.2 正向和反向速度场中界面还原测试

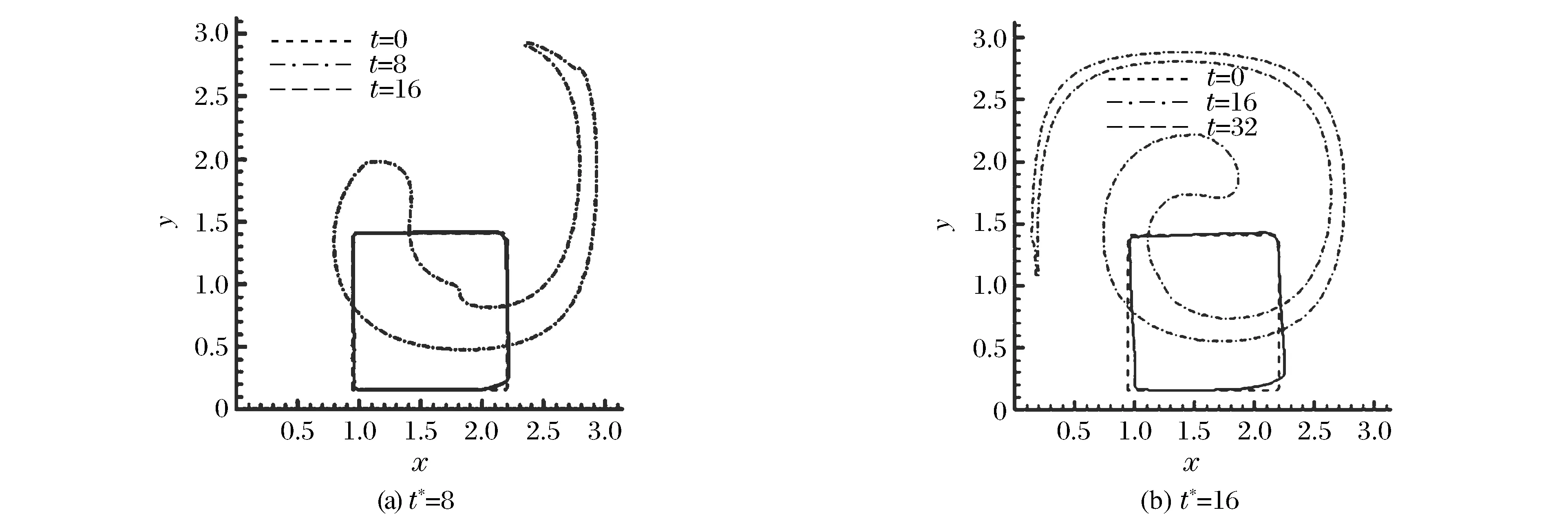
选取矩形在速度场中先正向旋转一段时间后，再反向旋转相同时间回到初始位置作为算例，同时采用改进的FT方法和Level-Set方法对该算例进行计算，通过比较两种方法计算所得旋转前、后矩形边界的变化情况，验证改进的FT方法的精确度。

矩形界面初始位置如图8所示，计算区域为[0,π]×[0,π]，矩形界面所围的区域为[0.3π,0.7π]×[0.05π,0.45π]。令u、v分别为x和y方向速度分量，当t

(4)

当t≥t*时，给定反向速度场为

(5)

式中：t*为速度场反向时刻。

图8 初始时刻界面位置Fig.8 Position of interface at initial time

通过理论分析可知：在t=t*时刻，界面变形最大；在t=2t*时刻，界面应当恢复到初始时刻的形状。在t*=8、t*=16两种条件下，采用改进的FT方法对矩形界面的演化情况进行数值计算，得到0、t*、2t*时刻界面的形状，如图9所示。

由于t*时刻速度场反向，再旋转t*后停止，此时界面恰好还原。因此，通过对计算停止时的界面形状与初始时刻矩形的比较，便能够反映出算法的准确性。从图9可以看出，旋转后界面位置与初始时刻位置基本重合，旋转过程中，界面形状得到了很好的保持，尤其是界面尖锐部分不会被抹平或者丢失。由此可见，改进的FT方法能够得到精度较高的模拟结果。

作为对比，采用Level-Set方法对相同条件下矩形界面的演化情况进行数值计算。计算采用二阶离散格式，在界面尖锐处采用自适应网格加密，每种情况分别给出0、t*、2t*时刻的界面形状，结果如图10所示。通过对图9和图10中结果进行比较可以看出，随着计算时间增加，改进FT方法对界面保持更好，精确度更高。此外，由于改进的FT方法只采用了一阶离散格式，并未采用自适应网格，因此，改进的FT方法耗费的资源更少，并且有进一步提高精度的空间。

图9 改进FT方法得到的不同时刻界面形状Fig.9 Interface shapes at different time using improved FT method

图10 Level-Set方法得到的不同时刻界面形状Fig.10 Interface shapes at different time using Level-Set method

4 结 论

提出了一种新的数据结构处理方法，建立了界面拓扑结构变化的追踪和模拟机制。该方法不但继承了传统FT方法能够准确模拟界面运动的优点，而且能够处理复杂界面拓扑结构的变化。在二维情况下，对2个算例数值模拟的结果显示，改进的FT方法能够准确地处理多物质边界拓扑结构的变化。

[1] OSHER S,SETHIAN J A.Fronts propagating with curvature-dependent speed:algorithms based on Hamilton-Jacobi formulations [J].J Comput Phys,1988,79(1):12-49.

[2] HIRT C W,NICHOLS B D.Volume of fluid (VOF) method for the dynamics of free boundaries [J].J Comput Phys,1981,39(1):201-225.

[3] CHERN I L,GLIMM J,MCBRYAN O,et al.Front tracking for gas dynamics [J].J Comput Phys,1986,62(1):83-110.

[4] GLIMM J,GROVE J W,LI X L,et al.Three-dimensional front tracking [J].SIAM J Sci Comput,1998,19(3):703-727.

[5] GLIMM J,GROVE J W,LI X L,et al.Robust computational algorithms for dynamic interface tracking in three dimensions [J].SIAM J Sci Comput,2000,21(6):2240-2256.