PBX炸药含各向异性损伤的黏弹性统计微裂纹本构模型初步研究*

张延耿，楼建锋，周婷婷，洪 滔，张树道

(北京应用物理与计算数学研究所，北京 100094)

1 引 言

PBX炸药是目前弹药中使用较为广泛的装药之一，其力学性能和安全性能一直受到设计者及使用者的关注。在日常勤务过程中，炸药会产生微裂纹、微孔洞等多种形式的损伤。由于炸药具有结构材料和含能材料双重属性，这些损伤一方面使炸药的力学性能劣化，并可能最终导致材料破坏；另一方面，损伤对“热点”的形成具有重要影响，进而影响炸药的感度、燃烧和爆炸性质。开展PBX炸药含损伤本构模型研究，有利于分析复杂环境中炸药材料力学性能的演化规律，对评估和提高炸药的安全性能具有重要意义。

近年来，人们对炸药材料细观结构变化规律的关注度越来越高，细观损伤模型的研究也越发被国内外研究机构及人员所重视，其中典型的工作是Dienes等人[1-2]提出的统计微裂纹(Statistical Crack Mechanics,SCRAM)模型，以及Bennett等人[3-5]对该模型的改进和发展。SCRAM模型基于微裂纹细观损伤机制，考虑微裂纹面法向的不同取向，能够描述币形裂纹从起裂、剪切、扩展到聚合的整个过程，被广泛应用于材料的动态响应特性分析。Dienes等人[2]结合炸药的宏观弹塑性，开展了PBX9501复合冲击实验数值模拟研究，结果表明，微裂纹的法向对材料的力学行为有重要影响。Bennett[3]和Hackett等人[4]基于Addessio和Johnson[5]提出的各向同性统计微裂纹模型，建立了黏弹性统计微裂纹模型(Visco SCRAM)，可用于描述炸药的宏观黏弹性和细观微裂纹损伤机制。相较而言，SCRAM模型不能描述PBX炸药宏观的黏弹性特征，而Visco SCRAM模型采用微裂纹所在单元压力的正负判断其扩展形式，忽略了微裂纹法向造成的影响，因而不能准确描述复杂应力状态下产生的损伤。

针对上述不足，在Dienes等人[1-2]、Bennett等人[3]及Zuo等人[6]的研究基础上，考虑损伤炸药在宏观上的的黏弹性特征及细观上微裂纹面的方向性，建立含各向异性损伤的黏弹性统计微裂纹本构模型(Aniso-Visco SCRAM模型)。并利用MATLAB数值计算程序，开展单轴加载条件下PBX9501的力学响应研究，分析不同法向微裂纹的扩展规律；根据计算所得不同应变率加载下的压缩和拉伸应力-应变曲线，分析破坏强度、临界应变的拉压异性及其随应变率的变化规律；最后，通过改变微裂纹数密度、初始微裂纹尺寸、微裂纹面摩擦系数和断裂表面能4个参数的取值，考察这些参数对计算结果的影响。

2 Aniso-Visco SCRAM本构模型的建立

Aniso-Visco SCRAM模型与Visco SCRAM模型结构类似，由一个包含多个并联Maxwell体的黏弹性体和一个由SCRAM模型定义的微裂纹损伤体串联而成[3],如图1所示，并采用如下简化：(1) 试件中随机分布着大量不同尺寸、不同法向的微裂纹，假设初始时刻微裂纹数密度各向同性分布，并且随裂纹尺寸的不同按指数规律变化；(2) 忽略微裂纹成核效应的影响；(3) 忽略微裂纹之间的相互作用。

在单个Maxwell黏弹性体模型中，分别采用线性弹性律、线性黏性律描述弹性和黏性[7-8]，具体表达式为

图1 Aniso-Visco SCRAM模型示意图(E为弹性模量)Fig.1 Schematic of Aniso-Visco SCRAM (E is the elasticity modulus)

(3)

式中：上标“ve”表示黏弹性；τ为松弛时间，τ(n)=η(n)/G(n)。

将5个Maxwell体并联，则总应变与分应变相等，总应力等于各分应力之和，即

(4)

(5)

(6)

在计算所有微裂纹扩展产生的应变εc时，由于考虑微裂纹面的法向因素，因此统计方程不再表示为如Addessio等人[5]提出的积分形式，而是不同法向上微裂纹应变分量的叠加求和。由均匀分布、法向矢量为n、半径为c的币形微裂纹引起的应变张量增量Δεc为[2]

(7)

实验结果指出，微裂纹数密度函数ρ(c,n,t)随尺寸不同而近似呈指数分布[9]

(8)

故所有裂纹扩展产生的应变为

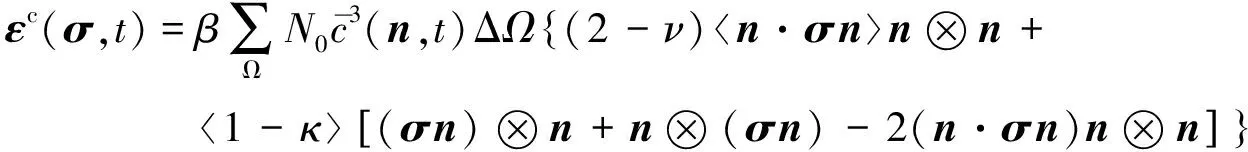
(9)

应变率的形式为

(10)

κ=μ-σn/sn

(11)

该模型以微裂纹尺寸的演化描述材料损伤，为求解上述方程，还需给出微裂纹扩展速度方程。仍采用Dienes等人[2]给出的表达形式，具体描述如下[10-13]

(12)

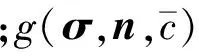
(15)

式中：f(σ,n)为应力函数。f(σ,n)依赖于微裂纹所处的张开或闭合状态，对于张开微裂纹(σn>0)

(16)

对于闭合微裂纹(σn≤0)

f(σ,n)=sn+μσn2

(17)

由上述模型的建立过程可知，材料体元内分布着大量具有不同法向的微裂纹，在远场三维应力σ作用下，可根据微裂纹面法向应力分量σn的正负判断微裂纹所处的状态——张开或闭合，进而由微裂纹扩展方程(12)式～(17)式可知其以不同形式扩展。模型中，微裂纹尺寸的增长表征材料体元的损伤破坏过程，因此随微裂纹面法向而形成了损伤的各向异性分布。采用(7)式～(10)式对不同法向微裂纹扩展而产生的应变叠加求和，得到宏观上全部微裂纹扩展产生的附加应变，通过耦合(4)式所描述的黏弹性变形，就组成了Aniso-Visco SCRAM本构模型的完整表述。

3 单轴应力加载下的计算结果与分析

在单轴加载条件下，假设加载方向沿x轴，则本构模型中(6)式和(10)式展开后为

式中：微裂纹法向矢量n=n1ex+n2ey+n3ez=cosψex+sinψcosθey+sinψsinθez，其中ex、ey、ez分别为x、y、z方向的基矢;H(x)是Heaviside阶跃函数。

由(4)式可知

(25)

(26)

由此可得单轴载荷作用下炸药的应力-应变曲线。

根据上述单轴载荷作用下的本构模型，结合微裂纹扩张方程(12)式～(17)式，采用MATLAB计算程序，开展如下内容研究。炸药材料为PBX9501，模型输入参数如表1所示。根据Dienes等人[2]的讨论，微裂纹面法向分布取值为481个。

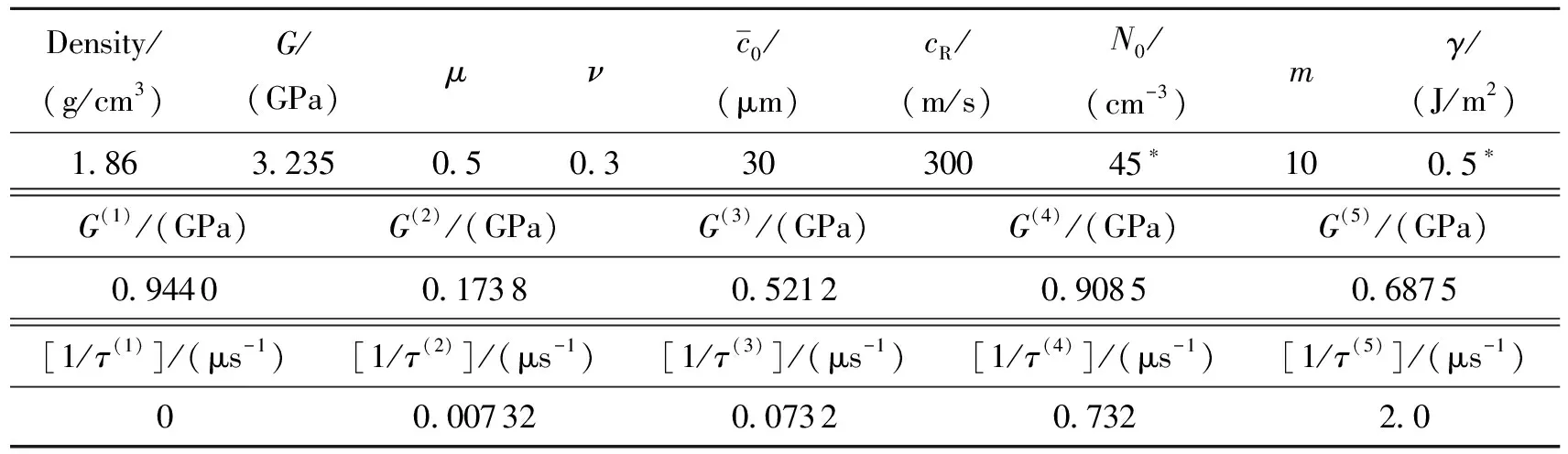
表1 Aniso-Visco SCRAM模型输入参数[2-4]Table 1 Constitutive model parameters for Aniso-Visco SCRAM[2-4]

3.1 微裂纹扩展的各向异性

数值计算中，μ=0.5，压缩和拉伸条件下对应的临界角分别为58°和0°。单轴压缩条件下(应变率为1 000 s-1),不同法向的微裂纹尺寸扩展情况如图2(a)所示，可以看出，最靠近临界角的ψ=57°处，微裂纹最先扩展，ψ=63°、48°及72°处的微裂纹依次紧随其后，而ψ=42°处由于能量释放率较低，微裂纹尺寸扩展很小。单轴拉伸条件下(应变率为1 000 s-1),不同法向的微裂纹尺寸扩展情况如图2(b)所示，可以看出，与加载方向相同的ψ=0°处微裂纹最先扩展，ψ=15°、30°、45°处的微裂纹依次紧随其后，而ψ=60° 处同样由于能量释放率较低，微裂纹尺寸扩展很小。可见计算结果与理论分析所得一致，证明了各向异性损伤模型在理论上的正确性。在Visco SCRAM模型中，所有方向的微裂纹均按同一规律扩展(见图3)，不能合理地描述相同加载条件下不同取向微裂纹的扩展方式，与实际物理机制存在差别；而本研究的Aniso-Visco SCRAM模型考虑了微裂纹面法向矢量的影响，可以清楚地描述微裂纹扩展的各向异性。

图2 具有不同法向的微裂纹尺寸扩展曲线Fig.2 Calculated crack extension curves of different orientations

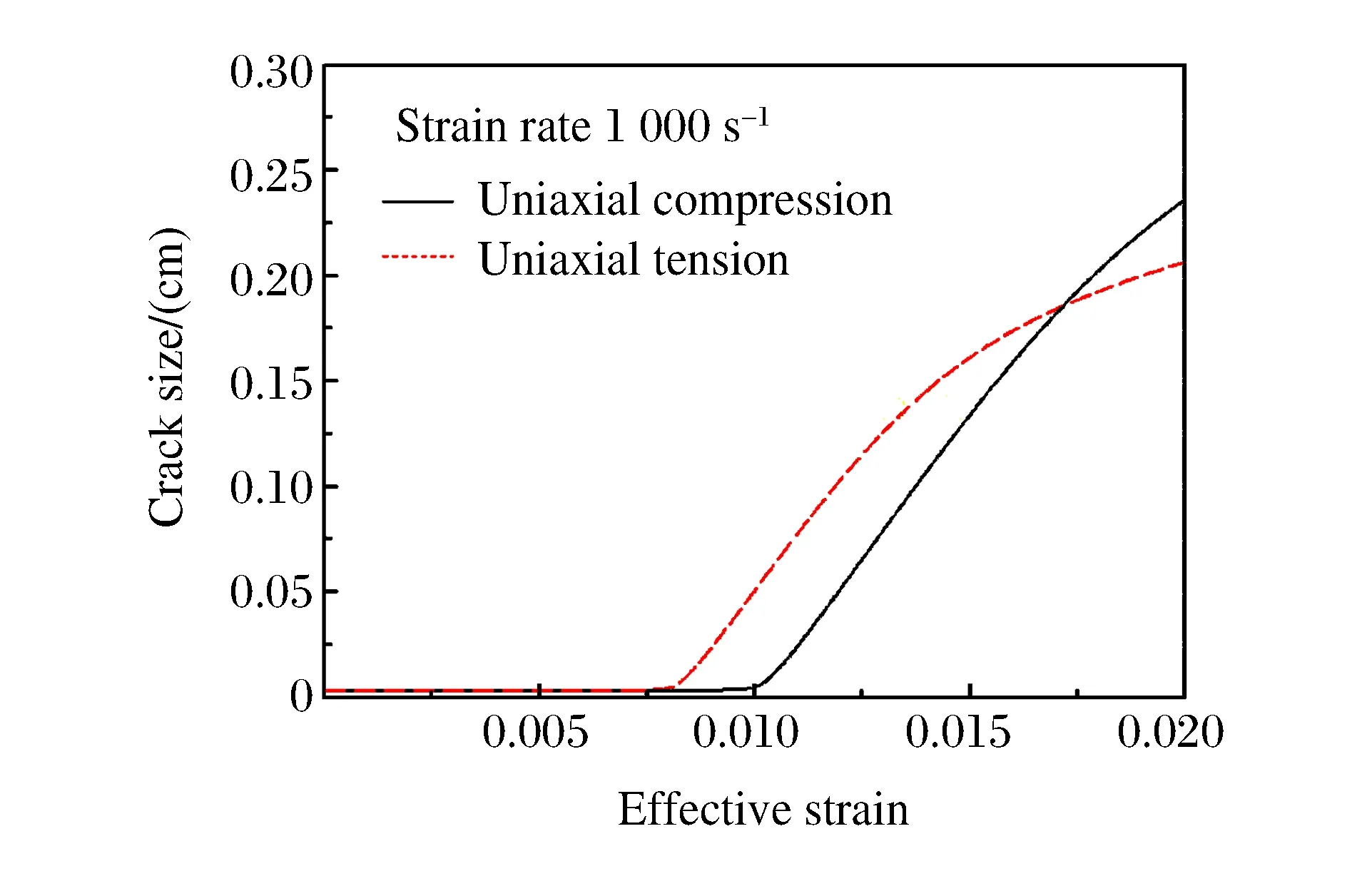
图3 Visco SCRAM模型中微裂纹尺寸扩展曲线Fig.3 Calculated crack extension curves of Visco SCRAM

3.2 应力-应变曲线的拉压异性

细观观测结果表明，在拉伸载荷作用下，PBX炸药以界面脱粘为主要破坏形式，其断面上可以观察到突出的颗粒和颗粒拔出后留下的凹坑；而在压缩载荷作用下，炸药颗粒发生破碎，以剪切破坏为主。不同的细观破坏模式造成炸药的拉伸强度比压缩强度小得多，具有明显的拉压异性[14]。

应变率为1 000 s-1时计算所得拉伸和压缩应力-应变曲线如图4(a)所示。从图4(a)中可以看出，在单轴压缩作用下，炸药的破坏强度(σc)和临界应变(εc)分别为51.0 MPa和0.012，与实验结果[2]相比，强度幅值接近，但临界应变稍小；而在单轴拉伸作用下，炸药的破坏强度(σt)和临界应变(εt)分别为24.1 MPa和0.005，均比压缩载荷下小得多。图4(b)为同等应变率条件下根据Visco SCRAM模型计算所得结果。Visco SCRAM模型中，拉伸和压缩加载条件下采用的等效应力表达形式接近一致，造成压缩曲线与拉伸曲线相差不大，因而不能很好地描述相同应变率下PBX炸药的拉压异性；而Aniso-Visco SCRAM模型根据不同取向的微裂纹所处的张开或闭合状态，采用不同的能量释放率方程描述其扩展规律，可以较好地描述PBX炸药的拉压异性。

图4 单轴拉伸和压缩作用下应力-应变曲线Fig.4 Calculated stress-stain curves under uniaxial tension and compression

3.3 单轴加载下的应变率相关性

不同应变率条件下的Hopkinson杆压缩实验和动态巴西实验结果表明，PBX炸药的模量、破坏强度和临界应变均随应变率的增加而增加，具有很强的应变率相关性。压缩条件下应变率加载范围为400～4 000 s-1时，计算结果如图5(a)所示，可以看出，随着应变率的增加，模量逐渐变大；在该应变率范围内，破坏强度由44.5 MPa增加至82.7 MPa，临界应变由0.011增加至0.018。可见单轴压缩载荷作用下，材料表现出较强的应变率相关性，与Gray等人[15]实验所得的变化规律一致。Visco SCRAM模型所得结果(见图5(b))与Aniso-Visco SCRAM模型的计算结果近似一致，原因是单轴压缩条件下所有微裂纹处于闭合状态，我们采用的叠加统计结果与原模型的积分统计结果趋于一致，进一步证明了新模型的可靠性。

图5 不同应变率条件下单轴压缩应力-应变曲线Fig.5 Calculated stress-strain curves under uniaxial compression at different strain rates

拉伸条件下应变率加载范围为100～1 000 s-1，计算结果如图6(a)所示，可以看出，随着应变率的增加，模量逐渐变大；在该应变率范围内，破坏强度由14.7 MPa增加至24.1 MPa，临界应变由0.004 0增加至0.005 6。在单轴拉伸载荷作用下，材料也表现出较强的应变率相关性，与赵玉刚等人[16]开展的动态拉伸实验所得变化规律一致。Visco SCRAM模型所得破坏强度(见图6(b))也随应变率的增加而增大，但幅值明显大于本研究结果；临界应变的变化不大，但幅值也大于本研究所得，且应变率为100 s-1时临界应变反而较大，初步分析认为，其原因是Visco SCRAM模型中求解等效应力的强度因子不合理。

图6 不同应变率条件下单轴拉伸应力-应变曲线Fig.6 Calculated stress-strain curves under uniaxial tension at different strain rates

3.4 部分参数讨论与分析

由上述建立的模型及数值计算分析可知，Aniso-Visco SCRAM本构模型参数较多，部分参数无法通过实验准确确定，且其取值对模型影响较大。以恒应变率(1 000 s-1)下的单轴压缩为例，分析微裂纹数密度、初始微裂纹尺寸、微裂纹面摩擦系数和断裂表面能4个参数对应力-应变曲线计算结果的影响，初始参数取值如表1所示。

3.4.1微裂纹数密度N0

微裂纹数密度N0的取值范围较宽，Dienes等人[2]取N0=45 000 cm-3，而根据Bennett等人[3]定义的初始缺陷尺寸计算得到N0=15 cm-3，因此我们考虑N0=45～45 000 cm-3范围内微裂纹数密度对计算结果的影响。计算结果如图7所示，随着微裂纹数密度的增加，材料的破坏强度、临界应变逐渐减小；应变软化段的变化规律也不一致，微裂纹数密度越大，材料初始软化段越陡峭，表明材料越容易发生崩溃式的脆性破坏。

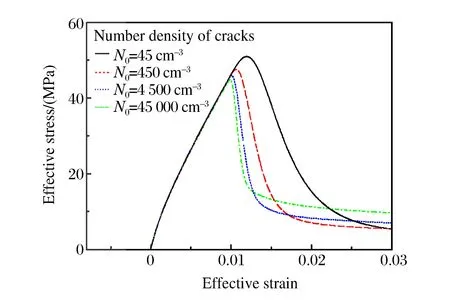
图7 不同微裂纹数密度取值的计算结果Fig.7 Calculated results under uniaxial compression with different number densities

图8 不同初始裂纹尺寸的计算结果Fig.8 Calculated results under uniaxial compression with different initial crack sizes

3.4.3摩擦系数μ

图9 不同微裂纹面摩擦系数的计算结果Fig.9 Calculated results under uniaxial compression with different frictional coefficients

3.4.4断裂表面能γ

断裂表面能γ是微裂纹扩展准则中的阈值参数，它的大小直接影响微裂纹所在单元开始发生劣化的应力水平。Dienes等人[2]给出HMX晶粒的断裂表面能为0.05 J/m2，而粘结剂却高达195 J/m2，但目前还未给出PBX9501的具体数值。我们以实验数据为基础，根据计算结果得到γ=0.5 J/m2。

图10 不同断裂表面能的计算结果Fig.10 Calculated results under uniaxial compression with different surface energies

为分析该参数对计算结果的影响，故考察取值范围γ=0.1～2.0 J/m2，计算结果如图10所示。由(12)式可知，断裂表面能增大，引起材料开始出现损伤劣化的阈值逐渐增加，即黏弹性变形区间变宽，因而造成其强度和临界应变显著增加。

综上所述，微裂纹数密度、初始微裂纹尺寸、微裂纹面摩擦系数和断裂表面能是描述炸药损伤演化过程的4个重要参数，它们的取值对数值计算结果有很大的影响。为更好地描述载荷作用下PBX炸药的力学特性和损伤破坏过程，需要对这些参数准确量化，其中，微裂纹面摩擦系数和断裂表面能可以通过实验测量获得，而微裂纹数密度和初始微裂纹尺寸需要开展讨论和定量分析。

4 结 论

基于PBX炸药宏观上的黏弹性和细观上具有不同法向的微裂纹损伤机制，建立了含各向异性损伤黏弹性统计微裂纹(Aniso-Visco SCRAM)模型，描述低速冲击载荷作用下材料的力学特性和损伤破坏过程，主要得到以下结论。

(1) Aniso-Visco SCRAM本构模型完成了细观各向异性损伤与宏观黏弹性的耦合，可以更好地描述PBX炸药在低速冲击载荷作用下的损伤机理和变形特征；

(2) 简化得到单轴应力加载下的本构模型，利用MATLAB计算程序，以PBX9501为例，计算得到压缩和拉伸条件下的应力-应变曲线，分析了具有不同法向的微裂纹扩展规律、PBX炸药材料破坏强度和临界应变的拉压异性以及应变率相关性，与Visco SCRAM模型相比，该模型更加合理。

(3) 微裂纹数密度、初始微裂纹尺寸、微裂纹面摩擦系数及断裂表面能等参数对具有不同法向微裂纹的扩展演化有很大影响，为更好地描述载荷作用下PBX炸药的力学特性和损伤破坏过程，需要结合实验和数值计算两方面进一步开展定量研究。

[1] DIENES J K.A statistical theory of fragmentation [C]//Proceedings of the 19th US Symposium on Rock Mechanics.Reno,Nevada:University of Nevada,1978:51-55.

[2] DIENES J K,ZUO Q H,KERSHNER J D.Impact initiation of explosives and propellants via statistical crack mechanics [J].J Mech Phys Solids,2006,54(6):1237-1275.

[3] BENNETT J G,HABERMAN K S,JOHNSON J N,et al.A constitutive model for the non-shock ignition and mechanical response of high explosives [J].J Mech Phys Solids,1998,46(12):2303-2322．

[4] HACKETT R M,BENNETT J G.An implicit finite element material model for energetic particulate composite materials [J].Int J Numer Meth Eng,2000,49(9):1191-1209.

[5] ADDESSIO F L,JOHNSON J N.A constitutive model for the dynamic response of brittle materials [J].J Appl Phys,1990,67(7):3275-3286.

[6] ZUO Q H,ADDESSIO F L,DIENES J K,et al.A rate-dependent damage model for brittle materials based on the dominant crack [J].Int J Solids Struc,2006,43(11):3350-3380.

[7] 王礼立.应力波基础 [M].北京:国防工业出版社,2005:148-151.

WANG L L.Foundation of stress waves [M].Beijing:National Defense Industry Press,2005:148-151.

[8] 叶敬棠,柳兆荣,许世雄,等.流体力学 [M].上海:复旦大学出版社,1989:375-379.

YE J T,LIU Z R,XE S X,et al.Fluid mechnics [M].Shanghai:Fudan University Press,1989:375-379.

[9] SEAMAN L,CURRAN D R,SHOCKEY D A.Computational models for ductile and brittle fracture [J].J Appl Phys,1976,47(11):4811-4826.

[10] EVANS A G.Slow crack growth in brittle materials under dynamic loading conditions [J].Int J Fract,1974,10(2):251-259.

[11] FREUND L B.Dynamic fracture mechanics [M].Cambridge:Cambridge University Press,1993.

[12] RICE J R.Comments on “on the stablility of shear cracks and the calculation of compressive strength” [J].J Geophys Res,1984,89(B4):2505-2507.

[13] KEER L M.A note on shear and combined loading for penny-shaped crack [J].J Mech Phys Solids,1966,14(1):1-6.

[14] 陈鹏万,黄风雷.含能材料损伤理论及应用 [M].北京:北京理工大学出版社,2006:25-30.

CHEN P W,HUANG F L.Damage theories and applications of energetic materials [M].Beijing:Beijing Institute of Technology Press,2006:25-30.

[15] GRAY G T Ⅲ,IDAR D J,BLUMENTHAL W R,et al.High- and low-strain rate compression properties of several energetic material composites as a function of strain rate and temperature [C]//The 11th International Detonation Symposium.Snowmass,Colorado:Los Alamos National Lab,1998:76-84.

[16] 赵玉刚,傅 华,李俊玲,等.三种PBX炸药的动态拉伸力学性能 [J].含能材料,2011,19(2):194-199.

ZHAO Y G,FU H,LI J L,et al.Dynamic tensile mechanical properties of three types of PBX [J].Chinese Journal of Energetic Materials,2011,19(2):194-199.