基于差分进化生物地理学算法的经济负荷分配
2016-04-25闫顺林田东旭艾书剑
闫顺林,谷 兵,田东旭,艾书剑
(华北电力大学能源动力与机械工程学院,河北 保定071003)
基于差分进化生物地理学算法的经济负荷分配
闫顺林,谷 兵,田东旭,艾书剑
(华北电力大学能源动力与机械工程学院,河北 保定071003)
针对智能算法在解决经济负荷分配问题时全局搜索能力和局部寻优能力不平衡的缺陷,提出了差分进化生物地理学算法。通过融合生物地理学算法和差分进化算法,并改进了算法中变异操作和替换重复个体策略,实现了的局部利用能力和全局搜索能力的平衡。通过建立求解经济负荷分配模型,兼顾考虑了燃料成本、阀点效应、环境成本以及各种约束条件,对具体案例仿真计算,将优化结果与生物地理学算法、差分进化算法和粒子群算法比较分析。结果表明差分进化生物地理学算法在收敛速度和优化质量方面较优,进而体现了该算法在解决经济负荷分配问题时的有效性和优越性。
经济负荷分配;生物地理学算法;差分进化;约束优化
0 引言
经济负荷分配(Economic Load Dispatch,ELD)问题是在满足各种约束条件下使电力系统经济性最优的约束优化问题。近年来,学者们针对ELD问题开展了大量研究工作,提出了众多数学规划方法和基于人工智能的优化算法,如差分进化、粒子群算法、生物地理学算法等[1,2],提高了ELD问题的计算效率及精确性,极大地推动了厂级节能调度技术的发展。
在利用智能算法优化ELD问题时,存在着一些不足,基于此,学者们对各类算法进行了改进,来弥补算法本身的不足。例如,李绍金[3]等提出了一种基于模糊自修正的粒子群算法以避免其易陷入局部最优;李冬[4]等提出了一种基于更新策略和状态转移规则改进的蚁群算法,避免了加速收敛中的停滞现象;周广闯[5]提出了一种将粒子群算法和单纯形算法相结合的混合算法,提高了局部和全局搜索能力;吴亮红[6]等人提出一种快速自适应差分进化算法,大大提高了收敛速率和鲁棒性。这些改进虽然在一定程度提高了算法能力,但是未考虑到算法的全局搜索能力和局部寻优能力的平衡,使算法计算效率在解决ELD问题时未达到最优状态。
针对不足之处,本文提出了基于差分进化算法(Differential Evolution,DE)改进的生物地理学算法(Biogeography Based Optimization,BBO),即差分进化生物地理学算法(BBO-DE)。BBO-DE算法结合了BBO算法强大的利用能力和DE算法高效率的搜索能力,并对BBO算法中的突变操作和变异策略进行改进,使得算法全局搜索能力和局部利用能力达到平衡。本文利用BBO-DE算法对ELD问题进行优化,并给出了负荷优化分配模型和算法步骤,结合相关算例与其他多种智能算法对比分析,计算结果表明,本文提出的BBO-DE算法是求解ELD问题的有效方法。
1 负荷调度的数学模型
1.1 目标函数
ELD问题是在满足系统运行约束条件下优化各个发电机组的功率,使得系统的总发电成本最小,即经济性最好。其目标函数可表示为:
(1)
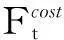
(2)
式中:ai、bi和ci均为发电费用系数。
当汽轮机进气阀突然开启时会出现拔丝现象,在机组的耗量特性曲线上会叠加一个波浪状起伏效果,这就是所谓的阀点效应[7](Valve Point Effect)。阀点效应对发电机组耗量特性曲线的影响不可忽略,需要在(2)式上叠加一个正弦函数。因此,考虑阀点效应的发电机耗量特性为:
(3)
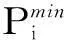
发电机组在发电的同时也会排放污染气体,污染气体主要包括CO2、SO2、NOx等,通过排放量和单位污染费用折算出环境成本[8]。则在单位时间内所产生污染气体排放量(单位为t/h)为:
(4)
式中:αi,βi和γi均为污染排放系数;D为总排放量。污染费用可以表示总排放量D与成本因子ω的乘积来得到:
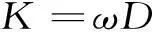
(5)
所以目标函数可表示为:
(6)
1.2 约束条件
(a) 功率平衡约束
功率平衡即发电机发出的有功功率总和与需求电量和总网损之和相等,如式(7)所示:
(7)
式中:PD和PL分别表示需求电量和总网损。
(b) 发电机有功功率约束[9]
(8)

(c) 爬坡速率约束
(9)
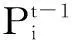
2 BBO-DE算法
2.1 生物地理学算法
BBO算法通过模拟生物物种在不同栖息地间移动和分布的情况来寻找最优解[10]。在BBO算法中,迁移和突变是两个重要的操作。栖息地之间通过迁移和突变操作,增强物种间信息的交换与共享,提高物种的多样性,逐渐向最优解进化。
假定栖息地数量为N,用D维向量表示,栖息地i的物种数量为Si,可能容纳的最大物种数量为Smax,Xij表示第i个栖息地Xi的第j维适应度变量,I和E为可能的最大迁入率和最大迁出率,栖息地Xi的迁入率λi和迁出率μi分别为[8]:
(10)
(11)
BBO算法中的突变操作是模拟栖息地生态环境的突变,使栖息地物种的数量急剧改变,增加了栖息地提供物种的多样性,为算法提供更多的搜索目标。栖息地Xi的变异率为mi,其表达式如下[11]:
(12)
式中:mmax为最大突变率;Pi为栖息地中物种数量对应的概率;Pmax为Pi的最大值。
2.2 DE算法
差分进化算法是一种随机并行直接搜索算法,它从随机群体开始按照变异、杂交、选择等过程不断迭代进化,根据个体适应度值保留优良个体,淘汰劣质个体,从而逐渐逼近最优解。DE算法原理简单,受控参数少,收敛速度快,是一种性能优异的全局优化算法。其中,变异是最重要的一项操作,变异过程中利用2个不同变量之间的差值和第3个变量组合产生相应的变异个体。变异策略有多种,常见的有rand/1、rand to best/1和rand/2,如式(13)~(15)所示[12,13]:
(1) rand/1
(13)
(2) rand to best/1
(14)
(3) rand/2
(15)
式中:r1~r5为[1,N]内互不相等的随机整数;F为变异参数;Yi,j表示第i个变异个体的第j维变量。
2.3 BBO-DE算法
BBO算法在迁移操作中,每个栖息地将自身适应度变量与其它栖息地进行共享,使得自己和其他栖息地的适应度水平得到提升,不断向最优解靠近[14]。但是,在迁移过程中并没有引入新的适应度变量,也就是说,迁移操作只是利用了已有的种群信息,这样便使得种群多样性不足。所以BBO算法的利用能力较强,而搜索能力较弱。而DE算法搜索能力出众,与BBO算法融合后,使算法的搜索能力和利用能力达到平衡,优化能力得以提升。具体融合策略为:种群中所有个体按照生物地理学算法进行更新,而最差的1/3个体还需按照公式(13)、(14)和(15)这3种变异策略进行变异进化。此外,BBO-DE算法与BBO算法相比,还有以下几点改进:
(a) 改进突变操作
在BBO算法中,突变操作是针对所有个体,并且突变后个体是随机产生的。若变异后产生的新的适应度变量为不可行变量,则会减缓寻优速度;对较优的适应度变量Xi,j进行突变操作产生的新适应度变量往往会劣于原适应度变量,反而影响了种群整体的质量。针对该问题,本文提出了基于母体的突变策略,如式(16)所示。
(16)
式中:等号左边的Xi,j为突变后新的个体;等号右边的Xi,j为突变前母体;Xr1,j为给定的范围内随机产生的一个个体;Fa为比例系数,其值在[0.35,1.25]之间。
(b) 改进替换重复个体策略
在标准BBO算法中,每次迭代后需要将系统中重复的个体进行替换,方法是用随机产生的新适应度变量代替重复的个体,若随机产生的个体较差则影响寻优进度,故提出一种改进的替换策略,见公式(17)。
(17)
式中:等号左侧的Xi,j为新适应度变量,等号右侧的Xi,j为原重复个体。这种替换重复个体策略既保证了系统的稳定性,也提升了物种的多样性。
综合2.1~2.3节,BBO-DE算法的流程如图1所示。
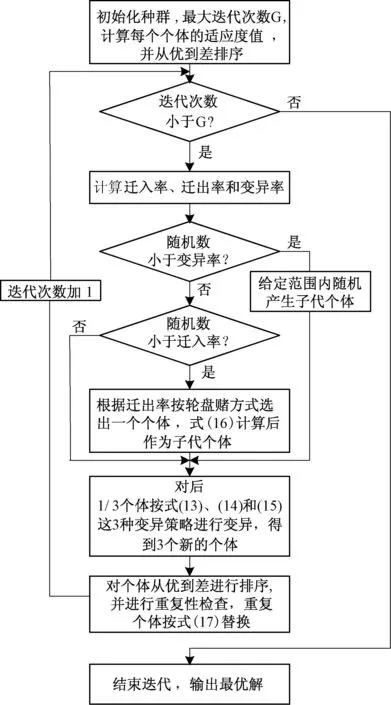
图1 BBO-DE算法流程图
3 算例仿真结果分析
为了验证改进BBO-DE算法的优势,在本节利用MATLAB软件(版本R3013a 8.1.0.604)进行了一系列仿真实验,并将BBO-DE算法与基本BBO算法、DE算法和标准粒子群(PSO)算法进行比较分析。
算例与参数。
以2×600MW+3×300MW系统为例,考虑环境成本,忽略网损。BBO-DE算法参数设置如下:种群规模N=100,最大迁入率I=1,最大迁出率E=1,最大变异率mmax=0.005,F=0.8,Fa=0.5,迭代次数为200。各发电机基本参数见表1,污染成本系数如表2所示,该系统典型日负荷需求如表3所示。
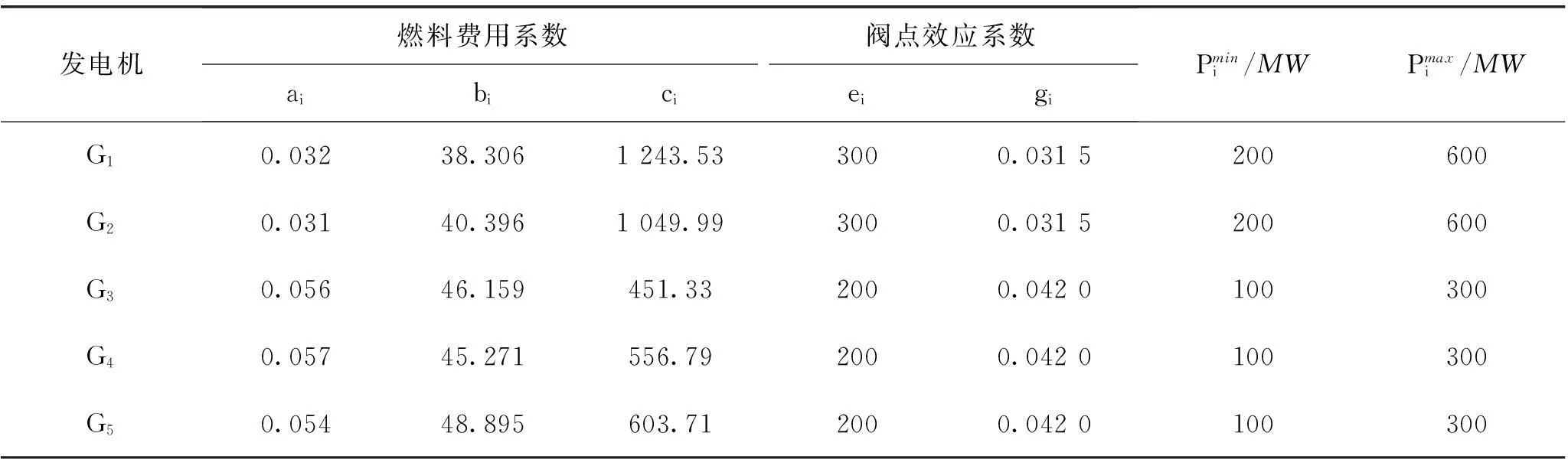
表1 发电机基本参数

表2 污染排放系数

表3 典型日负荷需求
(a) 算法收敛特性对比分析
为了对比明显,选取负荷较大的时段(时段12)进行对比分析,BBO-DE改进算法、BBO算法、DE算法和PSO算法这四种算法优化过程对比如图2所示。
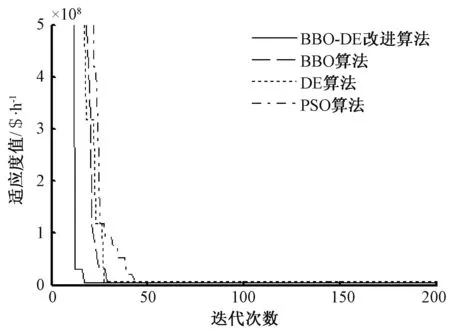
图2 四种算法收敛特性对比
由图2可以看出:(1)BBO算法前期相对于PSO算法具有较快收敛速度,但在进化中后期容易陷入局部最优解,这说明BBO算法具有较强的利用自身信息的能力,但缺乏与之相对应的探索新区域能力;(2)相对于BBO算法和DE算法,BBO-DE算法能够快速跳出局部最优解,以更快的速度收敛于全局最优解。
(b) 算法优化结果对比分析
在同等条件下,分别对四种算法独立计算30次,得到优化结果如图3所示。

图3 30次计算结果分布
由图3可以看出:BBO-DE改进算法优化结果的随机性明显小于其它3种算法优化结果的随机性,这是由于BBO-DE改进算法很容易跳出全局最优解附近的一些局部最优解,从而使优化结果较稳定。对30次独立计算的结果取平均数,可得到各个算法的平均优化总成本,如表4所示。
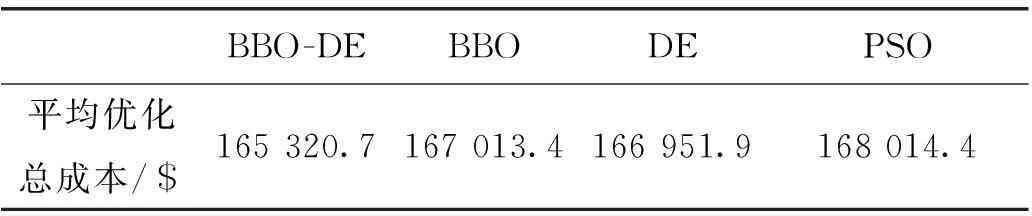
表4 30次独立计算平均优化总成本
从表4可以看出:BBO-DE改进算法所求得的平均优化总成本要比其它3个算法均小,即经济性更好。
(c) 各时间段机组出力分配与总成本
采用BBO-DE改进算法优化ELD问题所得到各个时间段对应的机组负荷分配情况如图4所示,从图中可以看出,不同时间段机组出力不同;各个时间段总费用如图5所示,不同时间段不同需求负荷所产生的费用不同,并且总费用变化趋势与需求负荷大致相同。
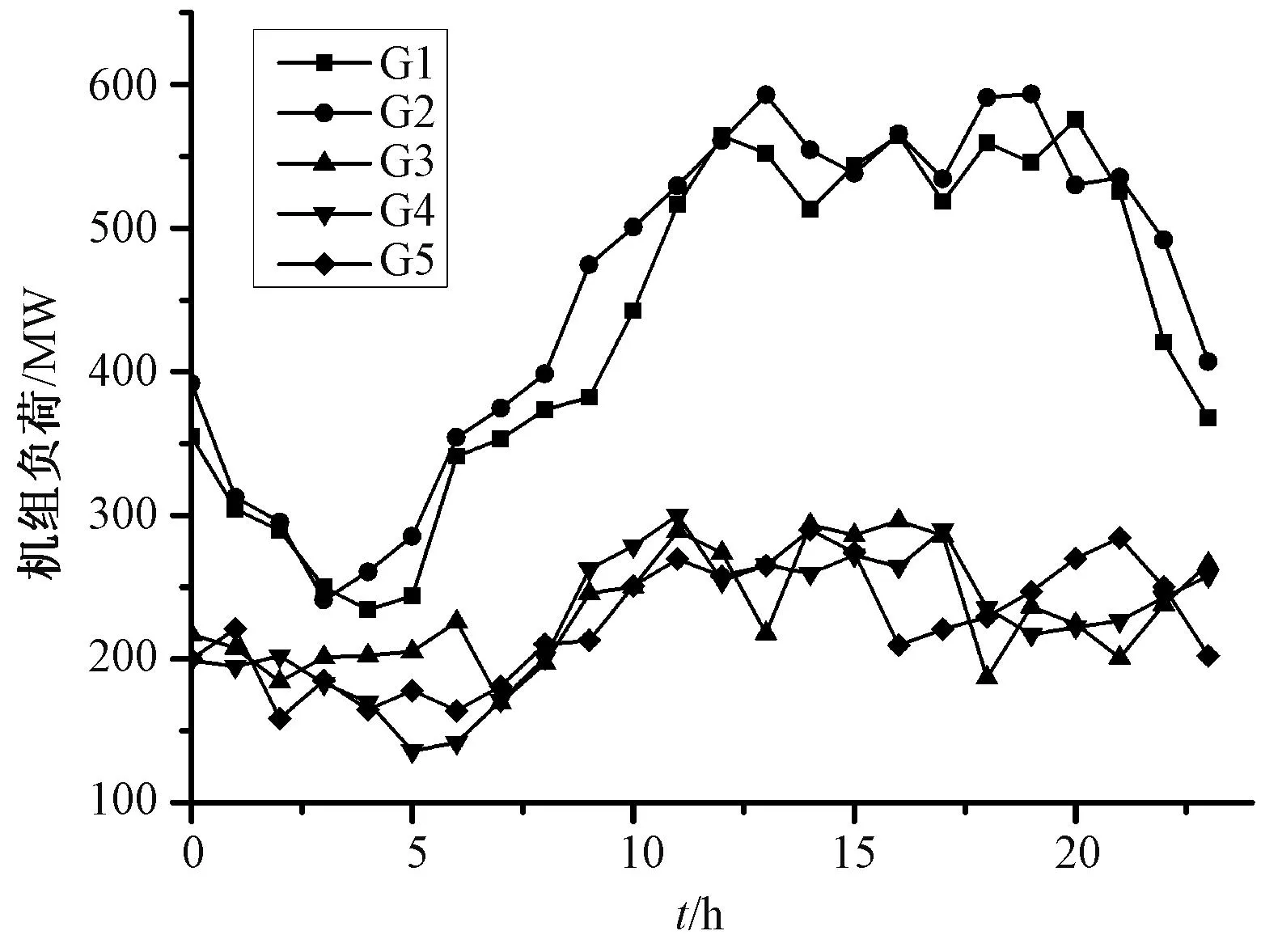
图4 各时间段机组负荷分配情况
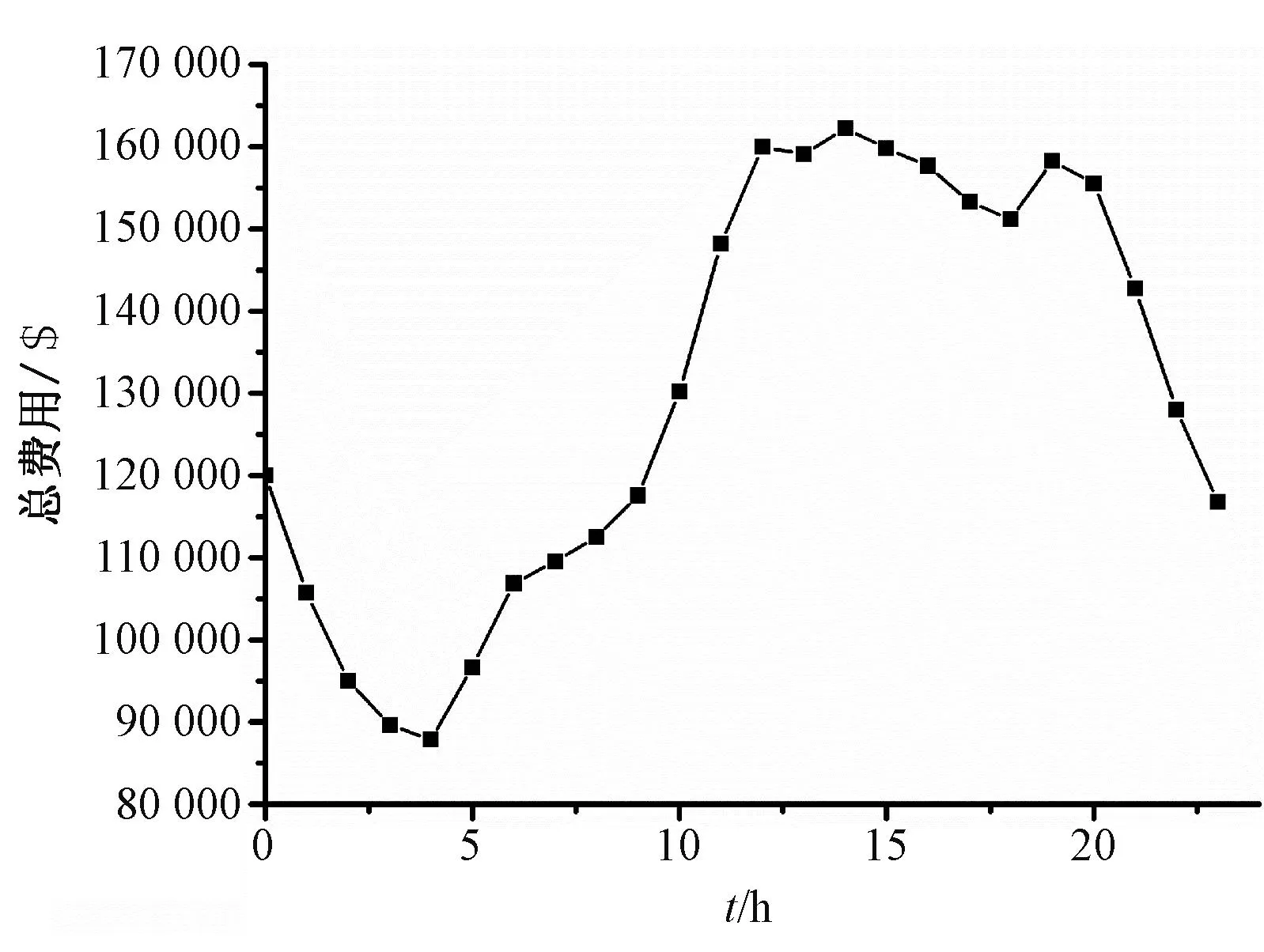
图5 各时间段总费用
4 结论
(1)本文提出的改进BBO-DE算法充分利用了BBO算法局部利用能力和DE算法的全局搜索能力,并且对算法中的变异操作和替换重复个体策略进行了改进,既使算法寻优过程更加可靠又保证了种群的多样性。
(2)在BBO-DE算法的基础上,针对电力系统中的ELD问题,本文将BBO-DE算法与标准BBO算法、DE算法和PSO算法进行了对比仿真计算,结果表明:BBO-DE算法在收敛速度和优化结果精确性方面均优于其它3种算法,进一步凸显了该算法在解决电力系统ELD问题上的优势性。
[1]翟俊义, 任建文, 周明,等. 基于模糊多目标粒子群算法的热电联供型微网环境经济调度[J]. 华北电力大学学报(自然科学版), 2015, 42(5):13-18.
[2]付殿峥, 黄国和. 基于因子交互分析的热电厂经济性优化研究[J]. 华北电力大学学报(自然科学版), 2014, 41(4):101-106.
[3]李绍金, 周任军, 周胜瑜,等. 电力系统环保经济负荷分配的模糊自修正粒子群算法[J]. 电力系统保护与控制, 2014(8):15-21.
[4]李冬, 刘建昌, 谭树彬,等. 改进蚁群算法在热精轧负荷分配优化中的应用[J]. 控制理论与应用, 2014, 31(8):1077-1086.
[5]周广闯, 陈璟华, 郭壮志,等. 基于混合智能算法的电力系统经济负荷分配[J]. 广东电力, 2014(10):41-46.
[6]吴亮红, 王耀南, 袁小芳,等. 基于快速自适应差分进化算法的电力系统经济负荷分配[J]. 控制与决策, 2013(4):557-562.
[7]蒙文川, 邱家驹, 卞晓猛. 电力系统经济负荷分配的人工免疫混沌优化算法[J]. 电网技术, 2006, 30(23):41-44.
[8]方丹. 基于综合效益指数的火电厂经济性分析[D]. 保定:华北电力大学,2011.
[9]闫顺林, 刘小旺, 贾朝阳. 带温度修正的小型分布式能源优化研究[J]. 电力科学与工程, 2015,31(9):7-10.
[10]张国辉, 聂黎, 张利平. 生物地理学优化算法理论及其应用研究综述[J]. 计算机工程与应用, 2015(3):12-17.
[11]徐志丹. 基于生物地理算法的多目标优化理论与应用研究[D]. 哈尔滨:哈尔滨工程大学, 2013.
[12]徐以坤, 余洋, 米增强,等. 基于微分进化的混合生物地理学约束优化算法[J]. 计算机工程与设计, 2015(7):1927-1931.
[13]LIU H, CAI Z, WANG Y. Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization[J]. Applied Soft Computing, 2010, 10(2):629-640.
[14]LEI X H, SHUUAI X X, QUAN Z Q. 1 DE/BBO: A Hybrid Differential Evolution with Biogeography-Based Optimization for Global Numerical Optimization[J]. Computer Engineering, 2010, 15(4):645-665.
Hybrid Biogeography Constrained Optimization for Economic Dispatch
YAN Shunlin, GU Bing, TIAN Dongxu, AI Shujian
( School of Energy Power and Mechanical Engineering,North China Electric Power University,Baoding 071003,China)
In the light of the defect of intelligent algorithms that global search ability and local search capability are imbalance in solving the economic load dispatch problem, a hybrid biogeography based optimization with differential evolution was proposed. By combining biogeography algorithm and differential evolution algorithm and improving balance algorithm mutation as well as replacing duplicate individual strategies, the abilities of local exploitation and global exploration are balanced and improved. The algorithm is used to solve the economic load dispatch problem by taking into account fuel costs, valve point effect, environmental costs and various constraints. It shows that the convergence rate and convergence precision are preponderant through simulation of specific cases, comparing with biogeography based optimization, differential evolution and particle swarm optimization.
economic load dispatch; biogeography based optimization; differential evolution;optimize;constrained optimization
2016-01-18。
闫顺林(1959-),男,教授,主要研究方向为热力系统节能理论及应用,E-mail:hdrd_gb@126.com。
TM73
A
10.3969/j.issn.1672-0792.2016.03.007
