舱段模型频率耦合噪声源的分离量化

李思纯, 宫元彬, 时胜国, 于树华, 韩闯

(1. 哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨 150001；2. 哈尔滨工程大学 水声技术重点实验室，黑龙江 哈尔滨 150001；3. 92677部队，辽宁 大连 116000)



舱段模型频率耦合噪声源的分离量化

李思纯1,2, 宫元彬1,3, 时胜国1,2, 于树华1,2, 韩闯1,2

(1. 哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨 150001；2. 哈尔滨工程大学 水声技术重点实验室，黑龙江 哈尔滨 150001；3. 92677部队，辽宁 大连 116000)

摘要：由于潜艇振动噪声源存在频率相互耦合现象，常规方法难以有效地解决耦合噪声源分离与贡献量化问题。采用一种新型多元统计分析方法-偏最小二乘回归分析方法来实现频率耦合噪声源的分离量化，该方法可同时提取反映输入/输出中最大信息且相关性最大的主成分，并能够在变量间存在多重相关性的条件下进行回归建模。仿真与舱段模型试验表明：当多激励源之间存在频率耦合时，能对噪声源进行分离和贡献量化，从而实现了噪声源对耐压壳体观测点贡献以及噪声源对辐射声场观测点贡献的排序，验证了偏最小二乘回归用于频率耦合源分离量化的可行性，为主要噪声源的控制提供了依据。

关键词：偏最小二乘回归；舱段模型；频率耦合；噪声源分离量化；耐压壳体；辐射声场

潜艇是一个复杂的噪声源分布体，潜艇内部机械设备及环境相互干扰，噪声源之间存在频率相互耦合现象，使多激励源的分离量化难度加大。确定水下声场中各传感器接收到的辐射噪声主要来自于哪些振动噪声源、确定潜艇主要振动噪声源的贡献量，可为潜艇噪声源控制提供依据[1-4]。

噪声源分离量化的方法主要有相关、分部运转和主成分等时域分析方法,以及功率谱、相干和偏相干等频域分析方法[5]。这些方法在分离相互独立噪声源时效果显著，但在实际情况下，传感器接收到的信号为耦合的噪声源信号，因此上述方法用于频率耦合噪声源分离使用受限[6-7]。为有效解决频率耦合噪声源分离量化问题，提出了一种基于偏最小二乘回归(partial least squares regression，PLS regression)[5]的频率耦合噪声源分离量化方法。该方法首先通过同时提取输入和输出中2个相关性最大的主成分，进而建立输入及输出对各自主成分的回归方程；其次利用交叉有效性原则确定是否停止迭代，迭代停止即可得到涵盖输入/输出重要信息的多个主成分；最后实现输出对输入的回归，通过回归方程各输入系数大小即可确定各输入源对输出观测点的贡献大小，从而实现噪声源的分离量化。 PLS法的显著特点体现在提取主成分过程中就已经解决了变量间多重相关性问题，因此对频率耦合噪声源分离有显著效果。

本文建立了多输入/单输出(multiple input single output,MISO)模型以及多输入/多输出(multiple input multiple output,MIMO)模型，对输入间存在频率耦合的噪声源进行了输出观测点到输入源的回归建模仿真研究。仿真结果及舱段模型振动噪声源分离量化试验验证了该方法的有效性。

1偏最小二乘回归理论

1.1基本原理

设自变量(输入变量):

因变量(输出变量):

式中：n为观测样本数，p和q分别为自变量和因变量个数。

为有效建立PLS回归模型，需要提取自变量和因变量中的主成分。分别在X和Y中提取成分t1和u1，需要满足2个条件：

1)t1和u1携带自变量和因变量中尽可能多的变异信息；

2)t1和u1相关性尽可能达到最强。

以上2个条件说明，t1和u1既要最大程度地承载X和Y中的信息，又要保证t1对u1具有很强的解释能力[5]。

PLS回归采用交叉有效性作为迭代停止准则。在第一主成分t1和u1被提取后，如果回归方程已经达到理想的精度，则算法终止；否则，分别从原始矩阵X和Y中减去第一主成分的贡献，之后对剩余输入/输出信息进行第二轮的主成分提取。如此迭代，直到达到理想的精度为止。如果最后对X共提取m个主成分t1,t2,…,tm，则PLS回归将通过施行yk(k=1,2,…,q)对t1,t2,…,tm的回归，然后再表达成yk关于自变量x1,x2,…,xp的回归方程[8]。

1.2偏最小二乘回归算法

PLS回归算法推导过程如下[8]：X和Y经标准化处理后的数据矩阵分别记为

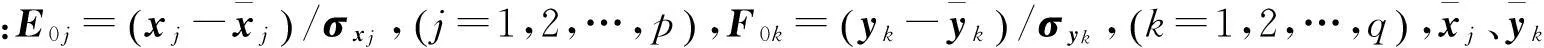
1)记t1是E0的第1个成分，t1=E0w1；w1是E0的第1主轴，是一个单位向量，即‖w1‖=1。

类似地，记u1是F0的第1个成分，u1=F0c1；单位向量‖c1‖=1是F0的第1主轴。

要求t1和u1尽可能地代表自变量和因变量中的数据变异信息，由主成分理论[9]，满足

var(t1)→max，var(u1)→max

同时，要求t1和u1达到最强的解释能力，根据典型相关理论[10]，满足t1和u1的相关性达到最大，即r(t1,u1)→max

在PLS回归中，等价于要求t1和u1的协方差达到最大，即

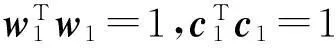
因此，在‖c1‖2=1和‖w1‖2=1的限制条件下，求解w1TE0TF0c1的最大值。采用拉格朗日算法，记

对上式分别求解关于w1、c1、λ1和λ2的偏导，并使偏导等于零，可得

(1)

(2)

(3)

(4)

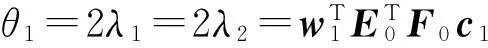
(5)

(6)

将式(6)代入式(5)，得到

E0TF0F0TE0w1=θ12w1

(7)

同理，可得

F0TE0E0TF0c1=θ12c1

(8)

求得w1和c1后，可得到主成分：

t1=E0w1

(9)

u1=F0c1

(10)

然后分别求E0和F0对t1、u1的3个回归方程：

E0=t1p1T+E1

(11)

(12)

F0=t1r1T+F1

(13)

式中:E1、F1*、F1为3个回归方程的残差矩阵，回归系数向量为

2)用E1和F1替代E0和F0后，继续求第2个主轴w2和c2以及第2个主成分t2和u2，即

t2=E1w2

(14)

将式(9)、(11)代入式(14)得

(15)

u2=F1c2

(16)

(17)

因此，可得回归方程为

(18)

(19)

3)同理可推导出第m个主成分tm，m的个数可由交叉有效性准则确定，交叉有效性准则是通过预测误差达到最小来确定提取主成分个数的准则:

(20)

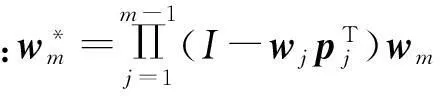
(21)

(22)

将式(9)、(15)、(20)代入式(22)推导出：

(23)

由式(23)可以看出，标准化因变量F0=(F01,F02,…,F0q)n×q可以表示成标准化自变量E0=(E01,E02,…,E0p)n×p的线性组合。

将公式

代入式(23)，即可得q个因变量的偏最小二乘回归方程式：

(24)

2噪声源分离量化仿真

2.1多输入单输出模型频率耦合信号仿真

多输入单输出仿真模型如图1所示，仿真参数设置为：输入信号x1(t)、x2(t)和x3(t)分别通过传递函数H1(t)、H2(t)和H3(t)，n(t)为加性高斯白噪声，得到的输出信号为y(t)。采样频率为4 096Hz，时间长度均为5s。

式中:f1=100 Hz，f2=200 Hz，f3=350 Hz，f4=500 Hz，f5=650 Hz，f6=1 000 Hz，φ1、φ2、φ3、φ4、φ5和φ6是以随机相位的形式出现的，同时引入加性高斯白噪声。由仿真条件可知，x1(t)、x2(t)和x3(t)输入之间都存在频率相互耦合信号，同时可知，x1(t)对输出信号的贡献最大，为最主要的振动噪声源，x3(t)次之，x2(t)的贡献最小。

图1　多输入单输出模型Fig. 1　Multiple-input/single-output model

根据PLS回归原理，分别将输出信号和3个输入信号在特征频率f1、f2、f3、f4、f5和f6上的能量作为观测样本，由偏最小二乘回归可得标准化变量的回归方程为

F=0.781 4E1+0.033 2E2+0.144 0E3

(25)

原始变量的回归方程：

y(t)=1.878 2x1(t)+0.982 1x2(t)+

1.045 4x3(t)+3.238 6

由原始变量的回归方程可知，x1(t)对输出y(t)的贡献最大，为最主要的振动噪声源，x3(t)次之，x2(t)的贡献最小，与仿真条件一致，PLS回归对多输入单输出耦合信号的分离量化的结果是有效的。由于原始变量的回归方程存在残差系数，因此由标准化变量回归方程结果，即式(25)可计算出x1(t)对y(t)的贡献比例为81.51%，x2(t)对y(t)的贡献比例为3.46%，x3(t)对y(t)的贡献比例为15.02%。

2.2多输入多输出模型频率耦合信号仿真

多输入多输出仿真模型如图2所示，仿真参数设置为：输入信号x1(t)、x2(t)和x3(t)分别通过不同的响应函数，代表不同的传递路径，n(t)为加性高斯白噪声，得到的输出信号为y1(t)、y2(t)和y3(t)。采样频率为4 096Hz，时间长度均为5s。

式中:f1=100 Hz，f2=200 Hz，f3=350 Hz，f4=500 Hz，f5=650 Hz，f6=1 000 Hz，φ1、φ2、φ3、φ4、φ5和φ6是以随机相位的形式出现的，同时引入加性高斯白噪声。x1(t)、x2(t)和x3(t)之间相互耦合，由仿真条件可知，x1(t)对y1(t)的贡献最大，x3(t)次之，x2(t)的贡献最小；x2(t)对y2(t)的贡献最大，x1(t)次之，x3(t)的贡献最小；x3(t)对y3(t)的贡献最大，x1(t)次之，x2(t)的贡献最小。

图2　多输入多输出模型Fig. 2　Multiple-input/multiple-output model

由PLS回归原理，分别将三输出和三输入信号在特征频率f1、f2、f3、f4、f5和f6上的能量作为观测样本，由偏最小二乘回归可得标准化变量的回归方程为

F1=1.137 7E1+0.009 6E2+0.170 8E3

(26)

F2=0.524 8E1+1.047 7E2+0.290 5E3

(27)

F3=0.312 7E1+0.003 5E2+1.108 4E3

(28)

原始变量的回归方程：

y1(t)=0.816 2x1(t)+0.058 1x2(t)+

0.261 7x3(t)-2.616 2

y2(t)=0.070 3x1(t)+1.180 3x2(t)+

0.083 1x3(t)-1.173 2

y3(t)=0.120 5x1(t)+0.011 4x2(t)+

0.911 9x3(t)-1.879 5

由原始变量的回归方程结果可知，x1(t)对输出信号y1(t)的贡献最大，为最主要的振动噪声源，x3(t)次之，x2(t)的贡献最小；x2(t)对输出信号y2(t)的贡献最大，x1(t)次之，x3(t)的贡献最小；x3(t)对输出信号y3(t)的贡献最大，x1(t)次之，x2(t)的贡献最小；与仿真条件设置相一致。各输入对各输出的贡献比例可由标准化变量的回归方程式(26)(28)计算出，如图3所示。因此，偏最小二乘回归方法对多输入多输出频率耦合信号的分离量化能够达到较理想的效果。

图3　多输入对多输出贡献直方图Fig. 3　Histogram of multiple input contribution to multiple output

3舱段模型试验研究

为了验证PLS回归算法在振动噪声源分离量化应用中的可行性，进行了舱段模型振动与噪声测试试验研究。振动噪声源分离量化综合试验舱段模型，如图4所示，舱段模型总长18.8m，外直径5.35m。在舱段内不同位置安装了3台振动激励设备A、B、C，分别为主疏水泵、海水泵和机械式激振机[11-13]。测量系统包括振动测量系统和水下声辐射测量系统。

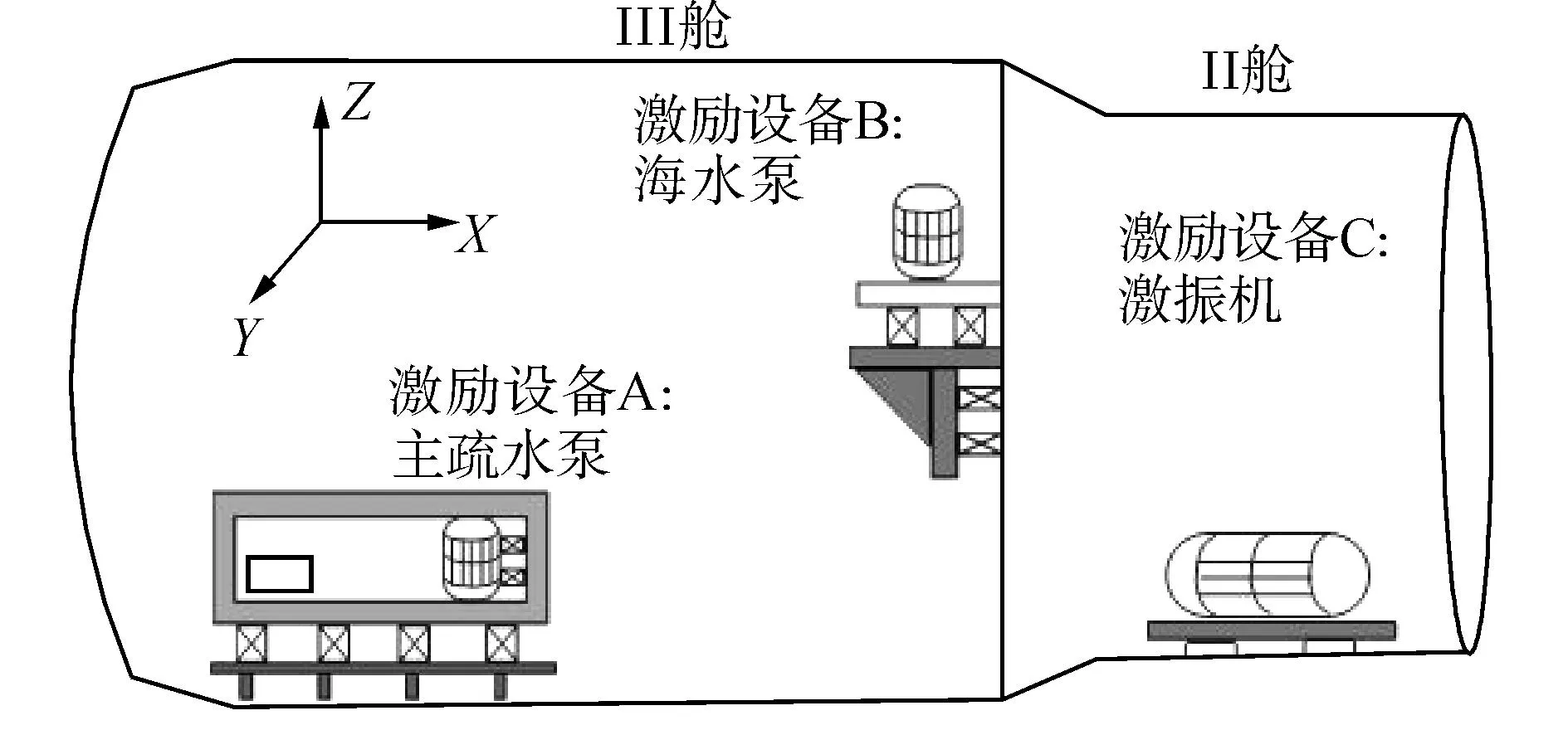
图4　舱段模型示意图Fig. 4　Diagram of cabin model

整个舱段包括2个舱体，II舱和III舱。主疏水泵通过隔振器侧挂在浮筏装置上。海水泵通过双层隔振装置安装在III舱内的II舱和III舱之间的舱壁上，激振机通过基座刚性安装在II舱中部的舱底。

为提取各主要振动噪声源的特征信息，分别在3台激励设备单开和全开的工况下，测量舱段内激励设备、耐压壳体振动信号和水下辐射声场的噪声。

3.1功率谱分析

3.1.1激励设备测点功率谱分析

在设备全开的工况中，对舱段模型中3台激励设备的振动测点进行功率谱分析得到的结果如图5。对主疏水泵上测点分析可知，50Hz为主疏水泵的基频，同时存在电信号的工频干扰。海水泵的测点，其功率谱是由49Hz基频及其倍频组成的，这说明海水泵是辐射声场和其他位置振动测点的49Hz频谱成分及其倍频的主要来源。激振机的振动特征线谱是41Hz，所以激振机是辐射声场和其他位置振动测点的41Hz频谱成分及其倍频的主要来源。激振机测点也存在49Hz和50Hz频谱成分，可见激励设备之间存在频率相互耦合信号。

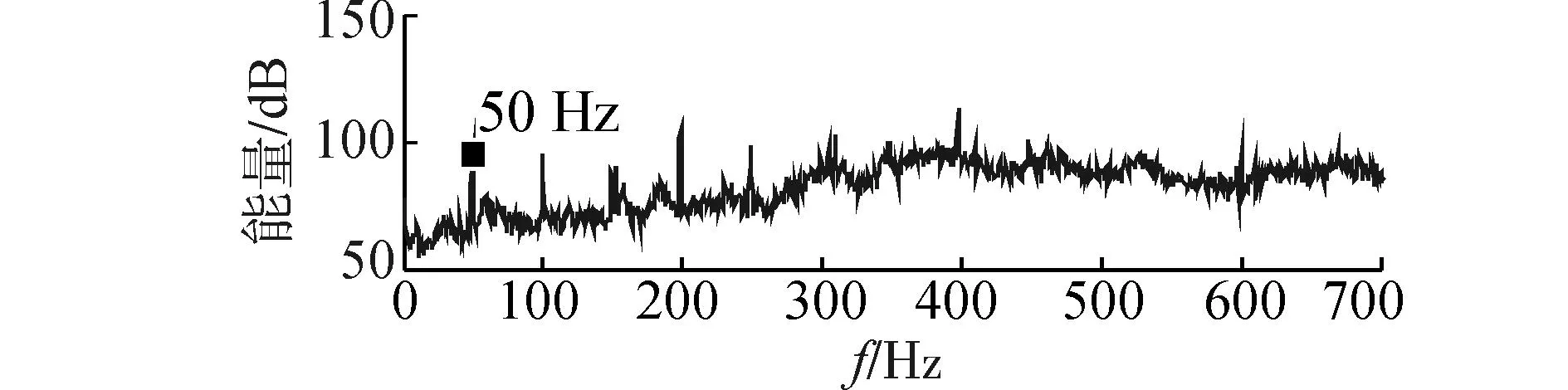
(a)主疏水泵测点功率谱

(b)海水泵测点功率谱

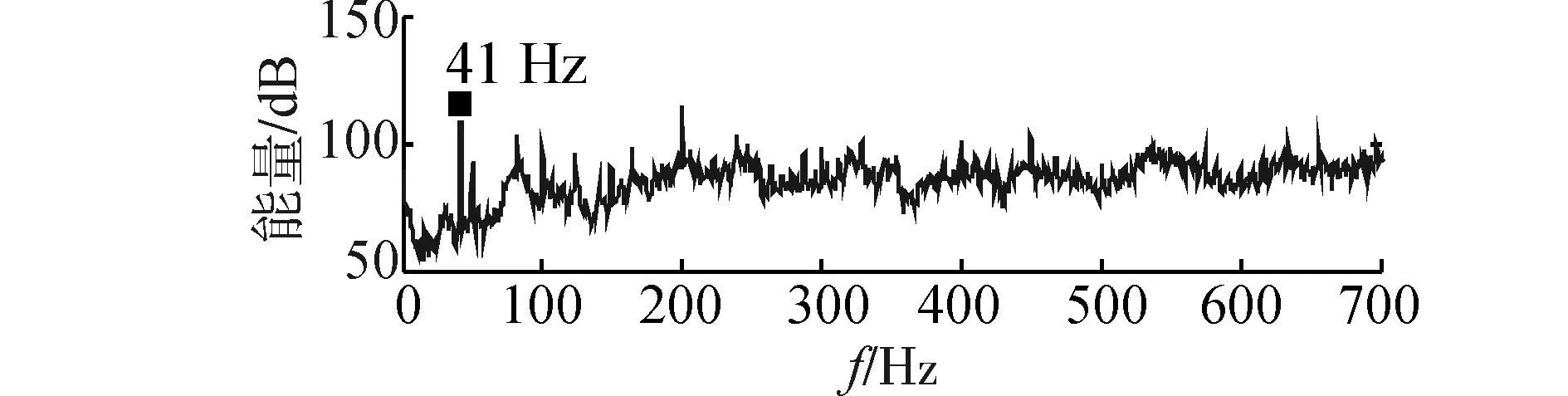
(c)激振机测点功率谱图5　设备全开激励设备测点振动信号功率谱Fig. 5　Power spectra of actuating equipments

3.1.2耐压壳体测点功率谱分析

舱段耐压壳体在主疏水泵、海水泵和激振机的共同作用下产生了振动，壳体测点功率谱如图6，耐压壳体1号测点在50Hz上的特征线谱略高于其他特征线谱，可大致看出主要是受主疏水泵和电信号的影响，而耐压壳体2号测点、耐压壳体3号测点在41Hz上的特征线谱远远高于其他线谱，可以推测主要激振机作用较大。

(a)壳体测点1功率谱

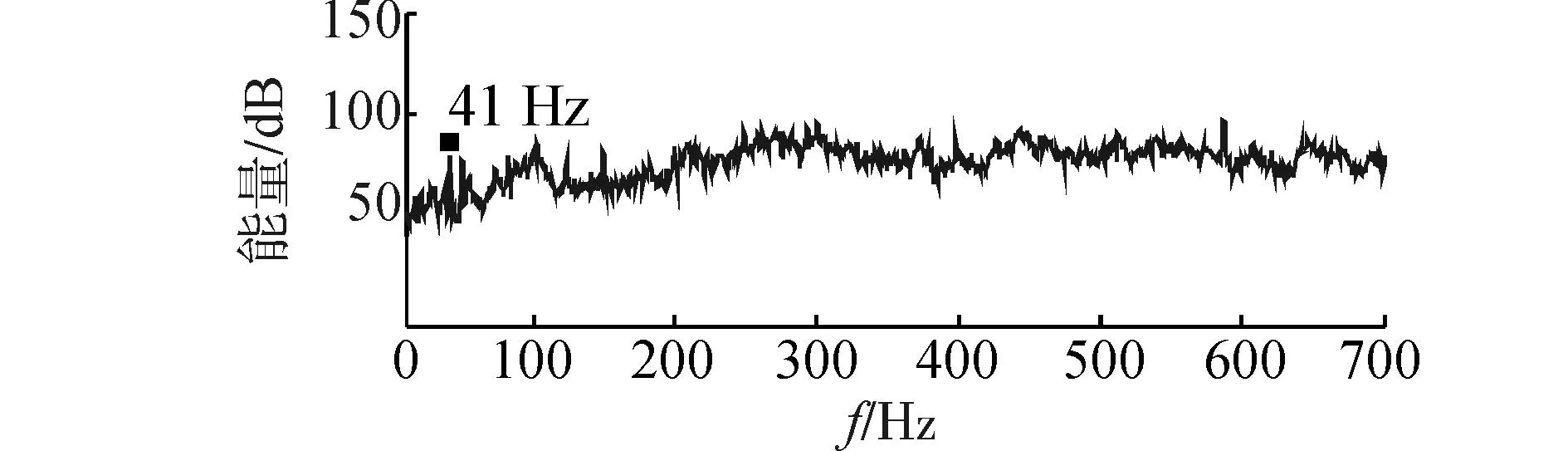
(b)壳体测点2功率谱

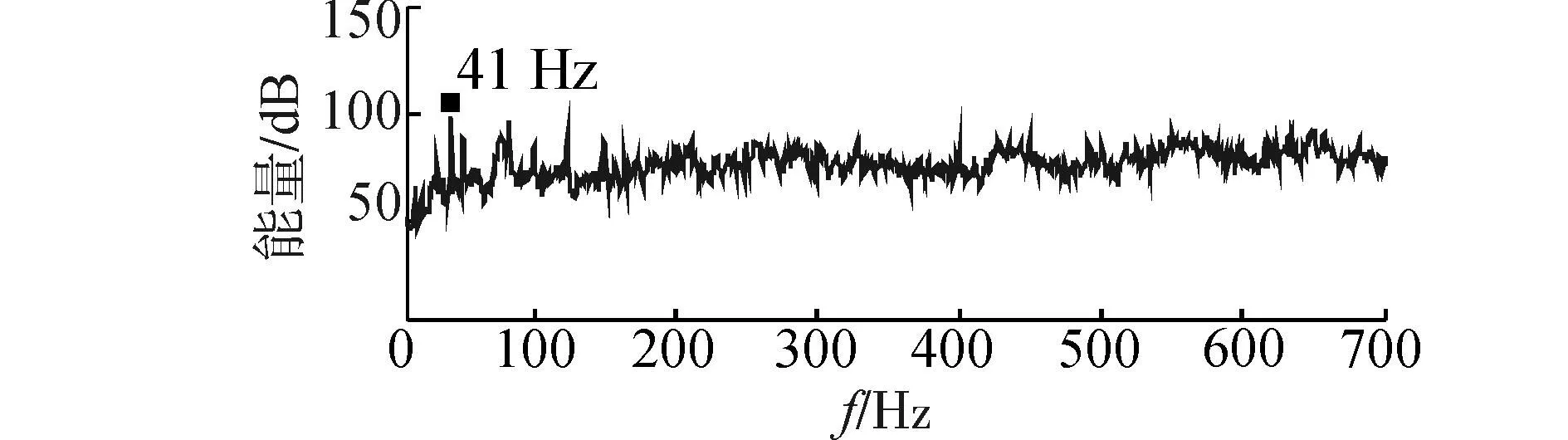
(c)壳体测点3功率谱图6　设备全开壳体测点功率谱Fig. 6　Power spectra of hull measure points

3.1.3水下辐射声场测点功率谱分析

分析舱段模型水下辐射声功率谱，结果如图7。从图7可以看出，功率谱分析可以清晰地展现舱段模型的水下辐射噪声信号的频谱结构特征，主要线谱包括：41、49、50、82、123、150、164、200、300、350、398、550、657Hz，根据各激励设备振动信号的特征信息，可知41、49、50Hz分别是激振机、海水泵和主疏水泵的基频，82、123、164Hz分别为41Hz的二倍频、三倍频和四倍频，150、200、300、350、550Hz是50Hz的倍频，同时50Hz与电信号存在工频干扰。

激振机在特征线谱41Hz上的能量大小明显高于其他设备上测点的特征线谱能量大小，所以可初步判断激振机是舱段模型中最主要的振动噪声源。

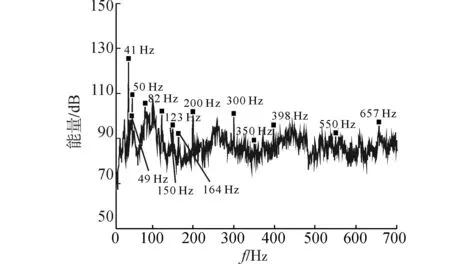
图7　设备全开水下辐射声场测点信号功率谱Fig. 7　Power spectrum of underwater acoustic field

3.2PLS回归分析

根据PLS回归原理，利用PLS回归进行噪声源分离量化，首先对输入信号和输出信号进行功率谱分析，提取输入和输出信号在各频率层内频谱上的能量，再将提取的能量作为偏最小二乘回归模型的数据观测样本矩阵，然后利用PLS进行回归建模，得出输出信号对输入信号的PLS回归方程，进而得出主要噪声源以及贡献大小，量化分离出结果，PLS回归信息处理流程如图8所示。

图8　偏最小二乘回归信息处理流程图Fig. 8　Flow chart of information processing based on PLS

3.2.1耐压壳体测点到水下辐射声场的MISO模型

在3台激励设备同时运转的工况下，将壳体测点1、壳体测点2、壳体测点3作为系统输入y1、y2和y3，将水下辐射声场测点作为系统输出z，建立壳体到声场的多输入单输出PLS回归模型。首先提取各输入和各输出在频率层内线谱上的能量，作为数据观测样本矩阵，然后计算相关系数如表1。

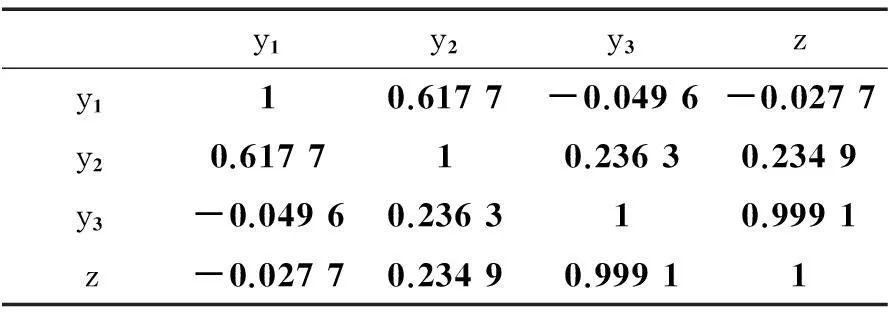
表1　水下辐射声场与壳体的相关系数

由表1可知，输入之间存在一定的自相关性，相关系数最高为0.617 7。输入与输出相关系数最高可达0.999 1，表明辐射声场与壳体存在较高的相关性，因此适合运用PLS回归分析。

根据PLS回归模型，得标准化变量的回归方程：

Z=0.063 8F1+0.010 1F2+0.958 4F3

原始变量的回归方程：

z=30.118y1+51.510 8y2+103.850 3y3-

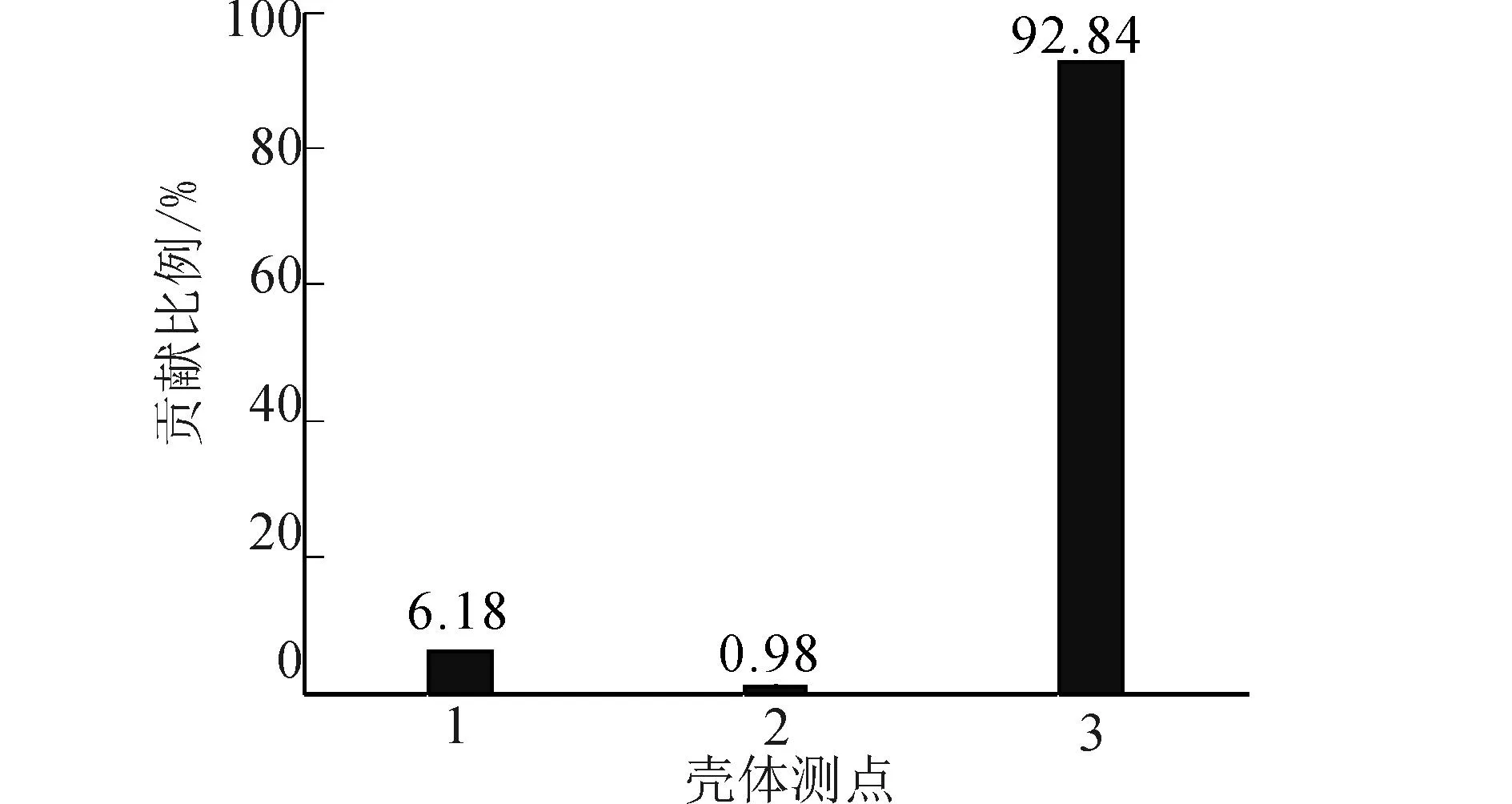
图9　耐压壳体测点对水下辐射声场的贡献直方图Fig. 9　Histogram of hull to underwater acoustic field contribution

由所得的原始变量的回归方程结果可知，壳体测点3对水下辐射声场的贡献最大，壳体测点1次之，测点2最小。测点1、测点2和测点3的布放位置分别是主疏水泵、海水泵和激振机周围耐压壳体上的测点，所得的量化结果与实际测点的位置有一定联系。其贡献比例可由标准化变量的回归方程计算所得，如图9所示。

3.2.2设备测点到耐压壳体测点的MIMO模型

在3台激励设备同时运转工况下，将主疏水泵测点、海水泵测点和激振机测点作为输入x1、x2和x3，将壳体测点1、壳体测点2、壳体测点3作为输出y1、y2和y3，建立激励设备到耐压壳体的多输入多输出PLS回归模型。首先提取各输入和各输出的在频率层内线谱上的能量，作为数据观测样本矩阵，然后计算输出与输入相关系数，如表2。

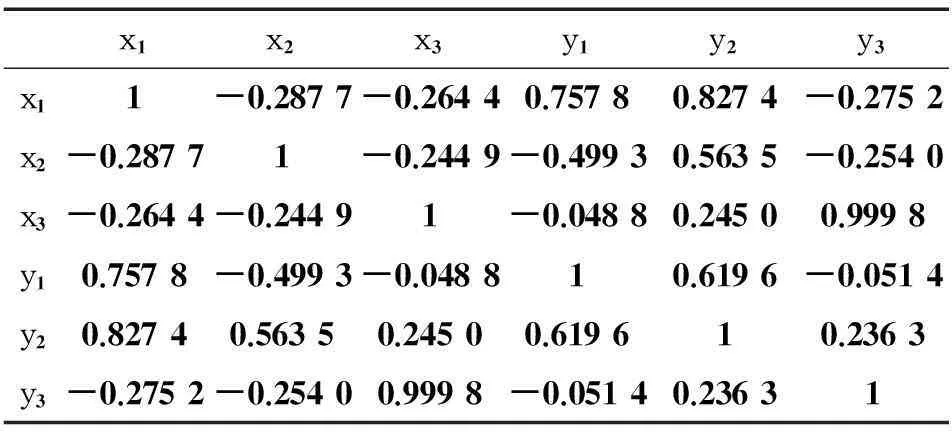
表2　壳体与设备的相关系数

由表2可知，输入之间存在一定的自相关性。输入与输出相关系数最高可达0.999 8，表明激励设备与壳体存在较高的相关性，因此，同样适合运用PLS回归分析。

根据PLS模型，可得标准化变量的回归方程：

F1=0.686 7E1-0.271 4E2+0.043 2E3

F2=0.844 3E1-0.155 2E2+0.359 8E3

F3=-0.015 9E1+0.041 0E2+0.936 5E3

原始变量的回归方程：

y1=

0.026 9x1-0.007 9x2+0.001 0x3+1.966 9×109

y2=

0.003 1x1-0.000 4x2+0.000 8x3+0.109 6×109

y3=

-0.004 9x1+0.005 2x2+0.092 9x3+0.669 8×109

由所得的原始变量的回归方程结果可知，对于耐压壳体测点1和耐压壳体测点2，主疏水泵的贡献最大；而对于耐压壳体测点3，激振机的贡献最大，海水泵次之，主疏水泵最小，其中正负号表示振动的方向。分离结果与功率分析和壳体测点位置相符合。各输入对各输出的贡献比例可由标准化变量的回归方程计算所得，如图10所示。

图10　激励设备对壳体测点贡献直方图Fig. 10　Histogram of equipments to hull contribution

3台激励设备振动噪声主要通过壳体测点传递到辐射声场，如图11所示。

图11　设备振动噪声传递路径示意图Fig. 11　Schematic diagram of noise sources transfer path

如果设备测点到耐压壳体测点的MIMO模型与耐压壳体到辐射声场测点的MISO模型相结合，将MIMO回归方程代入MISO回归模型中，便可以得到辐射声场测点z关于主疏水泵测点x1、海水泵测点x2和激振机测点x3的PLS回归方程。

所得标准化变量的回归方程为

Z=0.037 1E1+0.020 4E2+0.903 9F3

原始变量回归方程为

z=0.461 0x1+0.281 5x2+9.719 0x3+

由标准化方程计算所得的贡献比例如图12所示，主疏水泵、海水泵和激振机对辐射声场的贡献比例分别为3.86%、2.12%和94.02%。

为评估PLS回归算法对振动噪声源分离量化方法的有效性，选择分部运转法，即在主疏水泵、海水泵和激振机分别单开的情况下，分析水下辐射声场声压信号功率谱，得到3台激励设备在特征线谱上能量大小，并分别将每台激励设备的各个特征线谱能量求和得到总能量，从而得到主疏水泵、海水泵和激振机在特征线谱上对辐射声场信号贡献率分别为1.34%、0.98%和97.68%。

由于多源激励系统中各振动噪声源之间存在相干性以及潜艇舱段的复杂性，可能减弱甚至掩盖输入与输出之间的相干性，因此分部运转法分离量化的精度就会受到影响，但是通过PLS回归所得结果，基本与实际相符，激振机贡献最大，主疏水泵次之，海水泵最小。

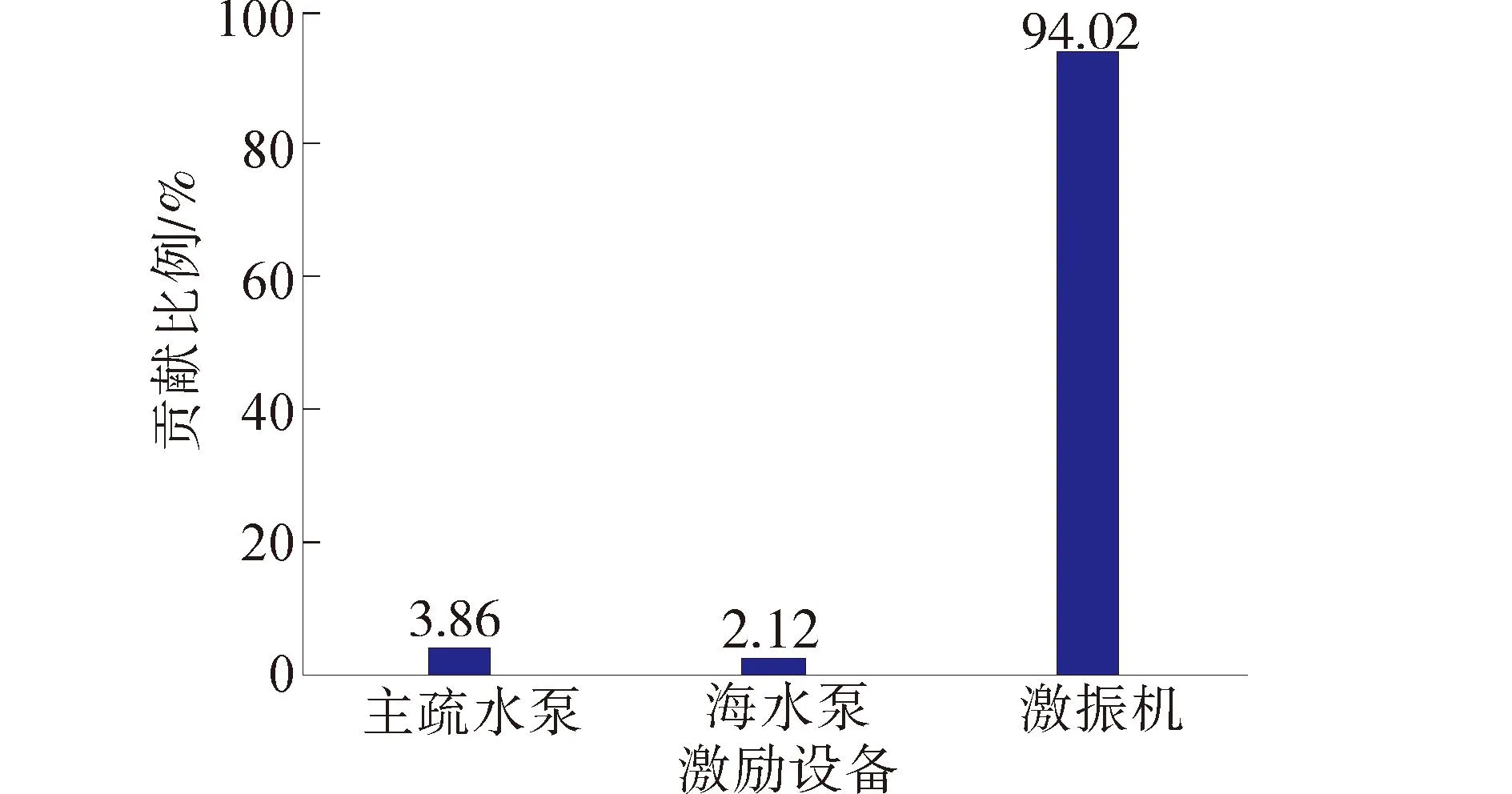
图12　激励设备对水下辐射声场的贡献直方图Fig. 12　Histogram of equipments to underwater acoustic field contribution

4结论

1)针对潜艇舱段模型，分别建立了激励设备到耐压壳体的MIMO模型和壳体到辐射声场的MISO模型，利用PLS回归成功的对其噪声源进行了分离量化。

2)PLS回归能够较好地分离量化潜艇舱段频率耦合噪声源。相对于主成分分析，偏最小二乘回归模型更具有先进性，其计算结果更为可靠，它的模型在实际系统中的可解释性也更强。

3)解决了多源激励系统中频率耦合噪声源的分离量化，为确定水下声场中传感器接收到的强辐射噪声主要来自于哪些振动噪声源及贡献量提供了依据。

参考文献：

[1]俞孟萨, 黄国荣, 伏同先. 潜艇机械噪声控制技术的现状与发展概述[J]. 船舶力学, 2003, 7(4): 110-120.

YU Mengsa, HUANG Guorong, FU Tongxian. Development review on mechanical-noise control for submarine[J]. Journal of ship mechanics, 2003, 7(4): 110-120.

[2]殷学文, 黄捷, 崔宏飞, 等. 潜艇结构振动和声学特性研究进展[J]. 振动与冲击, 2008, 27(4): 85-88.

YIN Xuewen, HUANG Jie, CUI Hongfei, et al. Advances in vibration and acoustic characteristics of a submarine[J]. Journal of vibration and shock, 2008, 27(4): 85-88.

[3]程广福, 刘文帅, 张文平. 舰艇辐射噪声源分离方法研究[J]. 哈尔滨工程大学学报, 2004, 25(5): 563-565.

CHENG Guangfu, LIU Wenshuai, ZHANG Wenping. Study of separation method of naval ship radiated noise sources[J]. Journal of Harbin engineering university, 2004, 25(5): 563-565.

[4]叶剑平. 潜艇主要噪声源分离技术综述[J]. 中国科技信息, 2012(6): 50-51.

YE Jianping. The Summarize on technology of separation of submarine main noise sources[J]. China science and technology information, 2012(6): 50-51.

[5]包研科. 数据分析教程[M]. 北京: 清华大学出版社, 2011.

BAO Yanke. Data analysis tutorials[M]. Beijing: Tsing hua University Press, 2011.

[6]江涌, 何琳, 章林柯. 同频带耦合噪声源的量化识别[J]. 机械工程学报, 2009, 45(8): 58-63.

JIANG Yong, HE Lin, ZHANG Linke. Quantitative identification of coupling noise source of same frequency band[J]. Journal of mechanical engineering, 2009, 45(8): 58-63.

[7]吴海平, 楼京俊, 刘文武. 相干噪声源贡献量排序分析方法[J]. 四川兵工学报, 2012, 33(11): 89-92.

WU Haiping, LOU Jingjun, LIU Wenwu. Sorting analysis of coherent noise sources contribution[J]. Journal of Sichuan ordnance, 2012, 33(11): 89-92.

[8]王慧文, 吴载斌, 孟洁. 偏最小二乘回归的线性与非线性方法[M]. 北京: 国防工业出版社, 2006: 111-115.

WANG Huiwen, WU Zaibin, MENG Jie. Partial Least-squares regression: linear and nonlinear methods[M]. Beijing: Nation Defense Industry Press, 2006: 111-115.

[9]何晓群, 刘文卿. 应用回归分析[M]. 3版. 北京: 中国人民大学出版社, 2011: 188-193.

HE Xiaoqun, LIU Wenqing. Applied regression analysis[M]. 3rd ed. Beijing: Renmin University of China Press, 2011: 188-193.

[10]李卫东. 应用多元统计分析[M]. 北京: 北京大学出版社, 2008: 259-269.

LI Weidong. Applied multivariate statistical analysis[M]. Beijing: Peking University Press, 2008: 259-269.

[11]门丽洁. 复杂机械结构振动传递特性分析方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012: 53.

MEN Lijie. The study of analyze methods for vibration transfer behavior of complex mechanism structures[D]. Harbin: Harbin Engineering University, 2012: 53.

[12]宫元彬, 李思纯, 杨德森, 等. 利用偏最小二乘回归的噪声源分离量化[J]. 声学技术, 2013, 32(6): 203-204.

Gong Yuanbin, LI Sichun, YANG Desen, et al. Noise source separation and quantification based on partial least squares regression[J]. Techincal acoustics, 2013, 32(6): 203-204.

[13]于树华. 潜艇舱段模型振动噪声源分离量化方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2013: 39-40.

YU Shuhua. Research on vibration and noise source separation and quantification of submarine cabin model[D]. Harbin: Harbin Engineering University, 2013: 39-40.

Separation and quantification of frequency coupled noise sources of submarine cabin

LI Sichun1,2，GONG Yuanbin1,3，SHI Shengguo1,2，YU Shuhua1,2，HAN Chuang1,2

(1. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China; 2. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China; 3.PLA 92677, Dalian 116000, China)

Abstract：Traditional methods do not effectively handle separation and quantification of coupled vibration noise sources in submarines. So a new multivariate statistical analysis method, partial least square regression (PLS), is presented, which can be used to separate and quantify frequency coupled noise sources. PLS has the characteristic of simultaneously extracting principal input/output components, including maximum information, correlation of input with output, and regression modeling with multiple correlations among variables. Simulation and cabin model experiments show that, when there is frequency coupling between multiple excitation sources, PLS is capable of sorting among the energy contributions of internal noise sources to submarine hull, submarine hull to underwater acoustic field, and noise sources to underwater acoustic field. The feasibility of PLS for frequency coupled source separation and quantification is proven. The method provides a basis for the control of the main noise sources.

Keywords：PLS regression; submarine cabin; frequency coupling; separation and quantification of noise source; pressure hull; radiated acoustic field

中图分类号：TB53

文献标志码：A

文章编号：1006-7043(2016)03-368-08

doi:10.11990/jheu.201409066

作者简介：李思纯(1963-), 女, 教授, 博士.通信作者：李思纯, E-mail: lisichun@hrbeu.edu.cn.

基金项目：长江学者和创新团队发展计划资助项目(IRT1228).

收稿日期：2014-09-29.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20151027.1100.002.html

网络出版日期：2015-10-27.