大数据的分布式机器学习的策略与原则

Eric P.Xing *, Qirong Ho, Pengtao Xie, Wei Dai

School of Computer Science, Car negie Mellon University, Pittsburgh, PA 15213, USA

大数据的分布式机器学习的策略与原则

Eric P.Xing *, Qirong Ho, Pengtao Xie, Wei Dai

School of Computer Science, Car negie Mellon University, Pittsburgh, PA 15213, USA

article info

Article history:

Received 29 December 2015 Revised 1 May 2016

Accepted 23 May 2016

Available online 30 June 2016

机器学习

人工智能大数据

大型模型

分布式系统

原则

理论

数据并行性

模型并行性

大数据的发展已经引领了对能够学习包含数百万至数十亿参数的复杂模型的机器学习系统的新需求，以保证足够的能力来消化海量的数据集，提供强大的预测分析（如高维潜特征、中介表示和决策功能）。为了在这样的尺度上，在成百上千台的分布式机器集群中运行机器学习算法，关键往往是要投入显著的工程性的努力——有人可能会问，这样的工程是否还属于机器学习的研究领域？考虑到如此“大”的机器学习系统可以极大地从根植于机器学习的统计和算法的理解中受益——因此，机器学习的研究人员应该不会回避这样的系统设计——我们讨论了一系列从我们近来对工程尺度的机器学习解决方案的研究中提炼的原则和策略。这些原则和策略从机器学习的应用连续跨越到它的工程和理论研究，以及大型机器学习的系统和架构的发展，目标是了解如何使其有效、广泛地适用，并以收敛和缩放保证支持。它们关注的是机器学习研究传统上注意较少的四个关键问题：一个机器学习程序怎样能分布到一个集群中去？机器学习计算怎样能通过机器间的交流连接起来？这样的交流是如何被执行的？机器间应该交流的内容是什么？通过揭示机器学习程序所独有的，而非常见于传统计算机程序中的基础性的统计和算法上的特点，并通过剖析成功案例，以揭示我们如何利用这些原则来同时设计和开发高性能的分布式机器学习软件以及通用的机器学习框架，我们为机器学习的研究人员和从业者提供了进一步塑造并扩大机器学习与系统之间的领域的机会。

© 2016 THE AUTHORS.Published by Elsevier LTD on behalf of Chinese Academy of Engineering and Higher Education Press Limited Company.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.引言

机器学习已经成为从原始数据中提取结构化信息和知识，将其转变成为不同应用的自动预测和运用假说的首要机制。这些应用如分析社会网络[1]、推理客户行为[2]；转译文本、图像和视频[3]；确定疾病和治疗方法[4]；操纵无人驾驶汽车[5]；跟踪网络安全异常活动[6]，及其他。机器学习的大多数应用都是由一个中等数量的发达的机器学习方法族系支持，其中，每种方法都体现了从模型设计到对算法的创新，甚至对软件应用的完善这一连串的技术要点，并吸引了来自研究和发展团体的日益增长的创新贡献。这些方法现代的例子包括图形模型[7-9]、正则贝叶斯模型[10-12]、非参数贝叶斯模型[13,14]、稀疏结构模型[15,16]、大幅度方法[17,18]、深度学习[19,20]、矩阵分解[21,22]、稀疏编码[23,24]以及潜在空间建模[1,25]。一个能确保数学合理性和结果可重复性的机器学习的普遍做法，是从业者和研究人员为某种机器学习方式(比如，通过一个卷积神经网络的深度学习模型，提供图像的语义解释)的一个特定应用的实例编写一个机器学习程序(使用任何通用的高级编程语言)。理想的情况是，这个程序预计将依托于各种硬件和云基础设施——笔记本电脑、服务器、图形处理单元(GPU)、云计算和虚拟机、分布式网络存储、以太网和Infi niBand网络(仅举几例)，以得到快速、准确的执行。这样，程序就是硬件无关但机器学习明确的(即无论硬件如何选取，对于数据都遵循相同的数学原理，并获得相同的结果)。

随着感官、数字存储和网络通信技术的进步，传统机器学习的研究与发展——擅长模型、算法和理论的创新——正面临日益盛行的大数据收集的挑战，如每分钟上传到视频共享网站的数百小时视 频①https://www.youtube.com/yt/press/statistics.html，或社交媒体中上亿用户产生的几千万亿字节(PB)数据②https://code.facebook.com/posts/229861827208629/scaling-the-facebook-data-warehouse-to-300-pb/。大数据的兴起也伴随着对包括数百万至数十亿参数的更高维也更复杂的机器学习模型的兴趣的增加，以支持日益复杂的数据，或者为了获得更高的预测精度(比如为客户提供更好的服务和医疗诊断)，支持更智能的任务(比如无人驾驶车辆和视频数据的语义解释)[26,27]。对这样大规模的数据运作如此大型的机器学习模型是超出单一机器的存储和计算能力的。这一差距已经激发了近来越来越多对于分布式机器学习的工作，其中，机器学习程序由研究集群、数据中心和云提供商使用成千上万的机器加以执行。从得到数学上等价的或类似于由单一机器产生的解的意义上说，以机器集群(p个机器)代替一个机器，就可以通过分布式机器学习程序实现几乎p倍的加速；然而，报告过的加速往往还远低于这个限度。例如，即使近来使用最先进的技术对主题模型的实现[28](文本分析的一种常用的方法)，由于在实现中的数学错误(如在文献[25]所示)，也无法用4×机达到2×加速，而利用MapReduce-like系统进行的深度学习，如Spark，也尚未用10×机达到5×加速 [29]。因此解决这种可量测性挑战就是分布式机器学习研究的一个主要目标，以减少运行大型机器学习应用的资本和运营成本。

考虑到大多数——如果不是全部的——主要支撑了当代大规模应用的机器学习算法的迭代收敛性质，一个人在第一眼可能自然地确定两种向可量测性发展的途径：以迭代次数度量的更快的收敛(在机器学习团体中也被称为收敛速度)，和以系统执行一个迭代的实际速度量度的更快的单次迭代时间(也被称为在系统中的吞吐量)。事实上，当前许多分布式机器学习研究者关注的主要焦点是算法的正确性和在大范围的机器学习方法中更快的收敛速度[30,31]。 然而，从算法研究到工业级的实现，由于其在系统上理想化的假设——例如，网络是无限快的假设(即零同步成本)，或所有机器以相同的速率执行算法(意味着没有背景任务，只有一个单一用户的集群，这对于许多用户共享的现实世界的研究和生产集群来说是不切实际的期望)，对于许多“加速”算法都很困难。另外，系统的研究者们聚焦在高吞吐量(每秒更多次迭代)和故障恢复的保证上，或许会选择假设机器学习算法将在非理想的执行模式下正常工作(如完全异步执行)，或者它可以容易地在一个给定的抽象概念上被改写(如MapReduce系统或顶点编程)[32-34]。在机器学习和系统的研究中，来自另一个方面的问题会变得简单化，从而可能会反过来掩盖降低分布式机器学习的资本成本的新机会。在本文中，我们提出了一个将以机器学习为中心和以系统为中心的想法相结合，并将机器学习算法(数学属性)和系统硬件(物理性能)的细微差别汇集起来，以让思想和设计从两端各自协力工作，并彼此增强的策略。

现有的许多通用的大数据软件平台提供了一种在正确性、执行速度和机器学习应用编程难易中特有的折衷方式。例如，数据流系统，如Hadoop和Spark[34]是建立在一个MapReduce系统的抽象概念上[32]，并提供了一个易于使用的编程接口，但较少关注机器学习性能，如容错、细粒度计算排序和加快机器学习程序的通信。因此，它们提供正确的机器学习程序执行，编程容易，但比机器学习的专业平台速度慢[35,36]。这种(相对的)速度欠缺可部分归因于用于Hadoop和Spark中的批量同步并行(BSP)的同步模型，其中，被分配给一组任务的机器必须等待最慢的机器完成，再进行任务的下一组程序(例如，所有程序必须在减速器开始前完成)[37]。其他的例子包括以图形为中心的平台，如GraphLab和Pregel，它们依存于一个为机器学习程序划分、计算排序、灵活的一致性控制开辟了新机会的基于图形的“顶点编程”的抽象概念；因此，它们通常对于机器学习来说较为准确、快速。然而，机器学习程序通常不被视为顶点程序(相反，它们在数学上表示为迭代收敛的定点方程)，需要通过不平凡的努力将其重写成顶点程序。在少数情况下，图像的抽象化可能会导致不正确的执行或达不到最佳的执行速度[38,39]。最近报告中介绍了参数服务器模式[28,36,37,40,41]，其为编写分布式机器学习程序提供了一个完全的“设计模板”或思考模式，但这不是一个像Hadoop，Spark，GraphLab和Pregel的编程平台或工作分配系统。考虑到为具体应用的实例编写机器学习程序的普遍机器学习实践，对机器学习从业者来说，一个有用的软件平台(作为替代)可以提供两种应用：①一套准备好的机器学习工具的实施，如随机近下降算法[42,43]、坐标下降算法[44]，或马尔可夫链蒙特卡罗算法[45]——可以在不同的机器学习算法族系中重复使用；②以及分布式机器学习集群操作系统，跨多种硬件分区和执行以支持这些工具的实施。这样的软件平台不仅降低了分布式机器学习研究的资本成本，而且通过更容易使用的编程库和集群管理接口降低了大型应用程序的人力成本(科学家和工程师的工作时间)，从而对研究有所促进。

随着对数据驱动的知识提炼、决策制定和持久学习越来越多的需要——这些是机器智能领域有代表性的标志——在未来几年中，计算大数据方面工作负载的主要形式可能会经历一个从用于确定性存储、索引和查询的数据库风格的操作，到机器学习风格的操作，如概率推理、约束优化和几何变换的快速转变。为了最好地完成这些计算任务，必须进行大量的数据传递，解决高维的数学程序，有必要重新审视传统系统架构中的原则和策略，并探讨在正确性、速度、可编程性和可配置性中达到最佳平衡的新设计。指导这样的探索所必需和关键的洞察力是：理解机器学习程序是以优化为中心，经常允许迭代收敛算法的解决方案，而不是一步或封闭形式的解决方案。此外，机器学习程序具有三个特性：①容错性，这使得机器学习程序能抵御中间计算中有限的错误；②动态结构的依存关系，其中，在模型参数间变化的相关性必须得到说明，以实现高效、近乎线性的并行加速比；③非一致收敛，其中，每10亿(或万亿)的机器学习参数都可以在大不相同的迭代次数下收敛(通常情况下，一些参数将收敛在2～3次迭代，而另一些则需要数百次)。这些性能可以与传统程序(如排序和数据库查询)相比，即传统程序以处理为中心，并且仅能保证如果每一步都是在原子正确的情况下进行，才能正确执行[32,34]。在本文中，我们将基于这些特性推导出分布式机器学习系统的独特设计原则；这些设计原则在机器学习正确性、速度和可编程性(同时通用于几乎所有机器学习程序)之间取得更高效的平衡，并组织成以下四个部分：①如何分配机器学习程序；②如何将机器学习计算和通信连接起来；③如何通信；以及④通信的内容。在深入探讨这些原则之前，首先让我们回顾一些关于机器学习迭代收敛算法的必要背景信息。

2.背景：机器学习迭代收敛算法

在存在少数特例的情况下，几乎所有的机器学习程序都可以被看作是以优化为中心，并固定为一个通用的数学形式的程序：

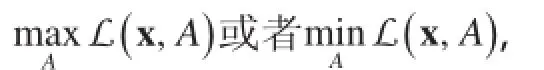
在本质上，一个机器学习程序尝试将N个数据样本(已标记或未标记，由实际应用决定)以表示(其中，yi只有在已标记的数据样本中出现)，代入由A表示的模型中。这种代入通过优化(最大化或最小化)一个综合目标函数L而实现，它由两部分组成：一个是损失函数f，用来描述数据如何适应模型；另一个是结构诱导函数r，通过给参数θ施加限制或者惩罚因子，将特定领域知识的预期应用具体化。方程(1)的简单性掩盖了函数f和r潜在的复杂结构及数据x和模型A潜在的巨大规模。此外，机器学习算法族系往往是由其中f，r，x和A的特点所定义。例如，用于图像分类的一种典型的深度学习模型，如文献 [20]中介绍的，模型A中会包含千万至十亿计的矩阵型模型参数，而损失函数f具有深度递归结构用来学习类似人类视觉皮层的图像分层表示。用于识别遗传疾病标志的结构化稀疏回归模型[4]可以使用重叠结构诱导函数+…，其中，Aa, Ab和 Ac是A的重叠子集，以遵守染色体重组的复杂过程。图形化的模型，尤其是主题模型，通常出现在数十亿的文件x中，即 N≥109，这数量很容易由社交媒体诸如脸谱网和推特产生——并且可能涉及数万亿的参数θ，以在如此多的数据中捕捉丰富的语义概念[26]。

除了指定方程(1)，还必须找到能够优化L的模型A参数。这通过在诸如随机梯度下降[42]、坐标下降[44]、马尔可夫链蒙特卡罗(MCMC)[45]和变分推理(仅举几例)等算法技术中选取一种算法来完成。将所选择的算法技术应用于方程(1)来产生一组迭代收敛的方程，其由机器学习从业者编写的程序代码实现，并可重复，直到收敛或满足停止准则(或常常是直到超出一个固定的计算预计值)。迭代收敛方程有以下一般形式：

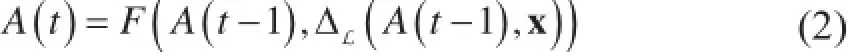
式中，t表示迭代次数。这个一般形式利用先前的迭代中的一个A(t - 1) 和数据x，产生下一个迭代的模型参数A(t)，其中使用了两个函数：①计算执行数据x和之前的模型状态A(t - 1)，并输出中间结果的更新函数ΔL(添加目标L)；以及②之后将这些中间结果组合产生A(t)的聚合函数F。为了符号的简单化，我们之后将从Δ的下标中省去L——毫无疑问本文中谈及的所有机器学习程序被认为具有一个明确的损失函数L(而不是缺乏这样一个损失函数的启发式算法或程序)。

现在让我们来看方程(1)和方程(2)这两个具体的例子，它们对于理解机器学习程序的独特性质将很有用。我们会特别关注任何机器学习程序的四个关键部分：①数据x和模型A；②损失函数f(x, A)；③结构诱导函数r(A)；以及④可用于这个程序的算法技术。

(1) 套索回归。套索回归[46]也许是结构化稀疏回归机器学习算法族系中最简单的例子，被用于以给定的向量值特征xi(即回归，它使用已标记的数据)预测响应变量yi——但基于在xi中只有几个维度或特征为yi提供信息的假设。作为输入，套索回归给出了N个训练样本x，以的形式，其中的特征都是m维向量。我们的目标是找到一个由权重向量A参数化的线性函数，这样，① ATxi≈yi，②m维参数是稀疏的(大多数要素都是零)：

或者更简洁的矩阵表示：

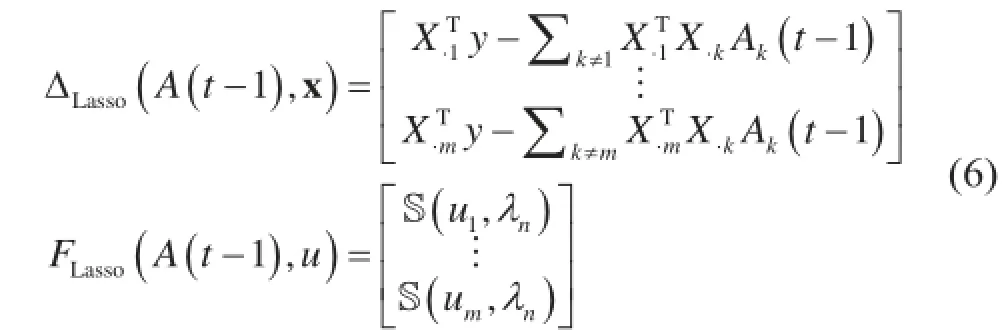
(2) 隐含狄利克雷分布主题模型。隐含狄利克雷分布(LDA)[47]是图形模型机器学习算法族系中的一员，也因其在一个文本文件的大型语料库中确定常见主题的能力，而被称为一个“主题模型”。作为输入，LDA是给定N个未标记的文件，其中，每个文件xi含有Ni个单词(在LDA文书中简称“记号”)，表示为xi=xi1,…,xij,…,xiNi。每个记号xij∈｛1,…,V ｝ 为一个整数，用来表示词汇集合V中的一个单词——例如，“机器学习算法”这个短语可以表示为xi=xi1,xi2,xi3=25,60,13(单词和整数之间的对应关系是任意的，且对LDA算法的精度没有关系)。

其中，

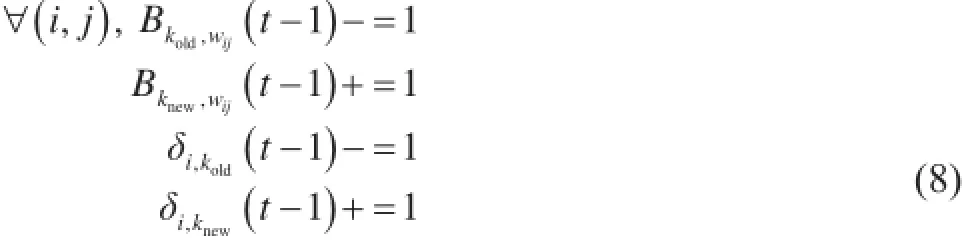
其中，+=和-=是自增、自减运算符(即δ，B和z都被原位修正)；～ P( )的意思是“抽样分布”，是给定现有值的zij的条件概率。更新在两个阶段进行：①在所有文件记号xij上执行方程(8)；②输出集合FLDA(A(t - 1), …)仅为恒等函数。

2.1.机器学习程序的独特性

为了在一个分布式的集群中加快执行大规模的机器学习程序，我们希望通过着眼于其如何通知分布式机器学习系统的设计来理解它们的属性。先了解机器学习程序“不”是什么会很有帮助：让我们考虑一个传统的、非机器学习的程序，比如用MapReduce排序。该算法首先随机在一个M映射集中分配要素进行排序x1,..., xN。映射将每个要素xi散列成键值对 (h(xi), xi)，其中，h是一个满足h(x) ＞ h(y)(如果 x ＞ y)的“保序”哈希函数。其次，对每一个独特的键a，MapReduce系统发送所有键值对(a, x)至标记“a”的减速器。然后每个减速器对其接收的值x运行顺序排序算法，最后减速器轮流(按键的升序排列)输出自己的排序值。

关于MapReduce排序要注意的第一件事，就是它是单通和非迭代的——只有单一Map和单一Reduce步骤是必需的。这与迭代收敛和重复方程(2)多次的机器学习程序相反。更重要的是，MapReduce是以操作为中心和确定性的，不能容许个人操作的错误。例如，如果一些映射器输出一个MIS散列对(a, x)，而a ≠ h(x) (作为讨论的基础，我们可以说这是由于断电恢复不当)，之后的最终输出将是错序的，因为x将在错误的位置输出。正是因为这一原因，Hadoop和Spark(支持MapReduce的系统)通过鲁棒容错系统提供强大的、可操作的正确性保证。这些容错系统当然需要额外的工程，需要额外更多基于硬盘的检查点和谱系树的形式的运行时长费用[34,49] ——但这些对不通过容错系统就可能无法正确执行的以操作为中心的程序是必要的。

这就引出机器学习程序的第一个属性：容错。不像MapReduce排序的例子，机器学习程序对中间计算的小错误通常是稳定的。在方程(2)中，即使有限数量的ΔL更新没有被正确计算或发送，机器学习程序仍然可以在数学上保证收敛模型参数A*达到最佳的设置——也就是说，机器学习算法能以正确的输出终止(尽管这样做可能需要更多的迭代)[37,40]。一个很好的例子是随机梯度下降(SGD)，这是很多机器学习程序常用的一种主力算法，应用范围从深入学习到矩阵分解和逻辑回归[50-52]。执行一个使用SGD的机器学习程序时，即使一个小的随机向量ε在每次迭代后添加到模型中，即A(t) = A(t) + ε，收敛仍有保证；直观地说，这是因为SGD总是为更新ΔL计算出最佳的A*的正确方向，所以移动A(t)会简单地以重新计算以适配的方向结束[37,40]。这个属性对分布式系统设计有重要的影响，因为系统不再需要保证完美的执行、机器间的通信，或从失败中恢复(这需要大量的工程开销和长运行时间)。进行近似的执行往往更便宜，特别是在资源被约束或限制的情况下(如有限的机间网络带宽)[37,40]。

除了容错，由于依存结构不是在对目标L或更新函数ΔL和F一次粗略的审视就能明确的，机器学习程序实际上比以操作为中心的程序更难执行。而依存结构出现在以操作中心的程序中就肯定是这样：在MapReduce排序中，减速器必须等待映射完成，否则排序将不正确。为了看看是什么使机器学习的依存结构独特，让我们在方程(3)中考虑套索回归的例子。乍一看，这个ΔLasso更新方程(6)可能看起来可以并行执行，但这只是部分正确。更仔细的审视

表明，对于第j个模型参数Aj，其更新取决于(t - 1)。换句话说，潜在的每个其他参数Ak都是可能的相关因素，因此模型参数A的更新顺序对机器学习程序的进程甚至正确性都会产生影响[39]。甚至还有一个在以操作为中心的程序中不存在的额外的细微差别：套索参数的相关因素不是二进制的(即不仅是“上”或“下”)，但可以通过机器学习程序状态和输入数据进行软赋值和影响。注意，如果= 0 (即数据列j与列k之间没有相关性)，则Aj和Ak互相不存在相关性，并且可以安全地并行更新[39]。同样，即使＞ 0，只要Ak= 0，那么Aj就不取决于Ak。这样的依存结构不受机器学习程序所限；对LDA主题模型更新方程(8)的仔细审视可以表明，吉布斯采样器更新xij(文档i中的单词记号j)取决于：①所有其他文件i中的单词记号，和②其他文件a中代表相同单词(即xij= xab)的所有其他单词记号b[25]。如果这些机器学习程序的依存结构没有被遵守，结果或者是用额外的机器(如用4×同样的机器得到＜ 2×加速)达到次理想的缩放比例[25]，甚至是压倒机器学习程序固有误差的完全的程序失败[39]。

机器学习程序的第三个特性是不均匀收敛，观察发现并非所有的模型参数Aj都将在相同数量的迭代后收敛至其最佳值Aj*——一种在单通道算法如MapReduce排序中出现的特性。在套索例子的方程(3)中，r(A)项促使模型参数Aj正好为零，实证发现，一旦参数在算法的执行过程中成为零，那它是不可能恢复到一个非零的值[39]。换句话说，成为零的参数已经(以虽然不是100%的高概率)收敛。这表明，通过对参数更频繁地执行ΔLasso，计算可能更优先向其仍然非零进行——这个策略的确降低了机器学习程序完成所花费的时间[39]。类似的不均匀收敛已在PageRank——另一种迭代收敛的算法中得到观察和利用[53]。

最后，值得注意的是，机器学习程序的一个子集具有紧凑的更新，经过仔细审视，发现更新ΔLasso比矩阵参数|A|的尺度明显缩小。在套索[方程(3)]和LDA主题模型[47]中，更新ΔLasso由于数据中的稀疏结构，通常只接触到模型参数的一小部分。另一个突出的例子是“矩阵参数化”模型，其中，A是一个矩阵(就像在深度学习中一样[54])，但个别更新ΔLasso可以被分解成几个小的载体(一种所谓的“低等级”的更新)。如果分布式机器学习系统在设计中将它考虑进去，那么这种紧凑可以大大减少存储、计算和通信成本，带来数量级上的加速[55,56]。

2.2.论数据与模型并行性

对于涉及百万兆字节数据、拥有上至数万亿模型参数的复杂机器学习程序的机器学习应用，使用单一的台式机或笔记本电脑来执行往往需要数天或数周时间[20]。这种计算瓶颈促使了许多机器学习程序用集群并行执行的分布式系统的发展[33-36]。机器学习程序通过在数据x或模型上A细分更新ΔL来并行执行——分别称为数据并行性和模型并行性。

需要注意的是，这两种类型的并行分别是互补和非对称互补的，因为同步数据和模型并行性是可能的(在某些情况下甚至是必要的)和非对称的，而数据并行性一般可应用于任何在数据样本x1,..., xN中具有独立同分布(i.i.d.)假设的机器学习程序。这样独立同分布的机器学习程序(从深度学习到逻辑回归、主题建模和其他许多方面)占据了大部分的实际机器学习使用，很容易通过目标L中的数据指标i求和验证[如套索方程(3)]。因此，当一个主力算法技术(如SGD)应用于L，得到的更新方程ΔL也将对i求和，这可以很容易地用多台机器并行处理，尤其是当数据样本数量N达到数百万或数十亿时。相反，模型并行性需要特殊注意，因为模型参数Aj并不总是能符合这种方便的独立同分布假设(图1)——因此，哪些参数Aj是并行更新的，以及更新ΔL所发生的顺序，可以导致多种结果：从用P台机器达到接近理想的P次加速，到没有用额外的机器带来额外的加速，甚至彻底的程序失败。先前讨论的套索依存结构(2.1部分)是模型参数的非独立同分布性质的一个很好的例子。现在让我们分别讨论数据和模型并行的一般数学形式。

(1)数据并行。在数据并行机器学习执行中，数据x = {x1,...,xN} 被划分和分配到并行计算的执行器或机器上(按p = 1,..., P索引)；我们可以用xp表示第p个数据分区。如果更新函数ΔL对数据样本i求最外层的总和(与平常的对数据独立同分布假设的机器学习程序一样)，我们就可以将ΔL进行数据子集的划分，并获得数据的并行更新方程，其中,ΔL(A(t - 1), xp)由第p个并行执行器执行：

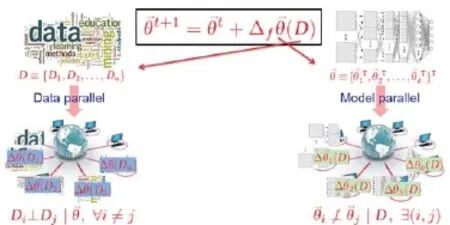
图1.数据和模型并行性之间的差异：数据样本总是有条件独立的给定模型，但有一些模型参数不是相互独立的。

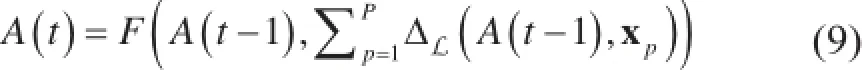
(2)模型并行性。在模型并行的机器学习执行中，模型A被划分和分配给执行器/机器p = 1,..., P，并通过运行并行更新函数ΔL在其中更新。与数据并行性不同，每个更新函数ΔL也需要调度或选择函数Sp,(t-1)，这也就限制了ΔL对一组模型参数A子集的操作(一个基本的用途是为了防止不同的执行器试图更新同一些参数)：

其中，我们省略了数据x，因为它没有被划分。Sp,(t-1)输出一组指数{j1, j2,...}，所以ΔL只在Aj1, Aj2,...执行更新；我们将这样的模型参数选择称为调度。模型参数Aj在一般情况下都不是相互独立的，可以确定的是模型并行算法只有当每个迭代并行更新被限制为一组相互独立(或弱相关)参数的子集时，可由Sp,(t-1)表示，才是有效的 [39,57-59]。

套索块坐标下降更新[方程(6)]能够以一个简单模型并行形式被容易地编写。在这里，Sp,(t-1)为执行器p在每次迭代选择同一组固定参数，我们称为 jp1,..., jpmp：

总之，划分数据样本和模型参数(xi, Aj)的空间成不相交的块，同时数据和模型并行性也是可能的。为了用P机器达到几乎完美的加速，LDA主题模型的吉布斯抽样方程[方程(8)]可以用这样一种块方式被划分(图2)[25]。

3.机器学习系统设计原则

机器学习程序的独特性质，再加上数据和模型并行性的互补策略，相互作用下会产生超出了由一般迭代收敛的更新方程(2)代表的理想数学观的设计考虑的复杂空间。在这种理想的观点下，我们希望Δ和F函数简单地需要平衡方程式(之前给出的套索回归数据和模型并行方程)来实现，然后由一个广泛目的的分布式系统执行——例如，如果我们选择了一个MapReduce抽象，就能编写Δ作为地图，F作为Reduce，之后再使用一种系统，如Hadoop或Spark来执行它们。然而，现实是最高性能机器学习的实现并非是建立在这样一种朴素的方式上；此外，它们还往往出现在机器学习的专业系统中，而不是广泛目的的MapReduce系统中[26,31,35,36]。原因是，高性能的机器学习远远超过了理想化的类MapReduce观点，并涉及并非在数学方程中显而易见的众多因素：对诸如用于数据并行性的数据批量大小，如何出于模型并行性进行模型划分，何时在执行器之间同步模型视图，算法的步长梯度选择，甚至是执行Δ更新的顺序等的考虑。

对机器学习性能空间的考虑即使对资深从业人员来说也可能是有难度的，我们的观点是，一个并行机器学习的系统接口是必要的，既便于对机器学习注意事项的组织性、科学性的研究，也能将这些注意事项安排到一系列开发新的分布式机器学习系统的高层次原则。作为安排这些原则的第一步，我们会将其根据四个层次的问题进行划分：如果一个机器学习程序方程[方程(2)]告诉系统“计算什么”，然后系统就必须考虑：①如何分配计算；②如何将计算与机器之间的通信连接起来；③机器之间如何通信；还有④通信的对象是什么。通过系统地解决在每一个问题上机器学习的注意事项，我们认为建立彼此补充和增益，并组装成一个在机器学习程序执行时间上获得数量级加速的完整分布式机器学习系统的子系统是可行的。

图2.LDA主题模型中同步数据和模型并行性高水平的说明。在这个例子中，三个并行的执行器在数据/模型块 在迭代1中操作，然后在迭代2中转移到块等。

3.1.如何分配：调度和平衡工作负载

为了并行化一个ML程序，我们首先必须确定如何最好地将其划分成多个任务——也就是说，我们必须将方程(2)中的单片Δ按照数据并行的形式[方程(9)]或模型并行的形式[方程(11)]，划分为一组平行的任务——甚至一种更复杂的混合形式。之后我们为了在有限的P执行器或机器池上执行，必须安排和平衡这些任务，那就是：①决定哪些任务并行在一起(更重要的是，其任务不应该被并行执行)；②决定任务将被执行的顺序；以及③同时确保每台机器分配的工作负荷均衡。

这三个决定已在以操作为中心程序的背景下经过了仔细研究(如MapReduce排序的例子)，带来了如Hadoop和Spark中使用的调度系统[34]。这样的以操作为中心的调度系统或许与不同的执行计划相结合——决定①～③的结合——取决于集群的配置、现有的工作负荷，甚至机器故障；然而更重要的是，它们确保以操作为中心的程序结果是完全一致，且每次是可重复的。然而，对于机器学习迭代收敛的程序，目标不是完美可重复的执行，而是模型参数A收敛至目标函数L的最优(即A以一个小的距离ε接近最佳值A*)。因此，我们要制定一个调度策略，其执行计划允许机器学习程序可以每次以同样的收敛性终止——我们把这个称为对于机器学习程序的“正确执行”。这样的策略之后可以被实现为一个调度系统，它能够创建不同于以操作为中心的机器学习程序执行计划。

(1)机器学习程序中的依存结构。为了产生一个对于机器学习程序正确的执行计划，有必要了解机器学习程序有着怎样的内部依存关系，以及如何通过单纯的并行化打破或违反这些依存关系以减缓收敛。不同于以操作为中心的程序比如排序，机器学习程序具有容错性，并能自动地从数量有限的违反函数依赖的数据中恢复，但太多的违反会增加收敛所需要的迭代数量，使并行机器学习程序利用P机器的加速未达最佳标准、达不到P次阶。让我们通过套索和LDA主题模型的实例程序，了解这些依存关系。在套索模型的并行版本[方程(12)]，每个并行执行器p∈{1,…, P}执行一个或更多(t - 1)形式的ΔLasso计算，之后可以用于更新Aj。注意到这个计算通过(t - 1)项依存于所有其他参数Ak, k ≠ j ，依存关系的量级与第j项和第k项的数据维度之间的相关性，以及参数 Ak(t - 1)的当前值成正比。在最坏的情况下，相关性和Ak(t - 1)都可能很大，因此顺序更新Aj, Ak(即在两个不同的迭代中t, t + 1)会导致与并行更新(即同时在迭代t中)不同的结果。文献[57]指出，如果相关性大，则并行更新将比顺序更新需要更多的迭代收敛。它直观地表明，我们不应该“浪费”计算来试图并行更新高度相关的参数；相反，我们应该寻求为并行更新调度非相关的参数组，同时对相关参数进行顺序更新[39]。

对于LDA主题模型，让我们来回忆一下ΔLDA更新[方程(8)]：对于每个单词记号wij(在文件i的位置j)，LDA吉布斯采样器更新模型参数B、δ(A的一部分)的四个要素：Bkold,wij(t - 1) - =1，Bknew,wij(t - 1) + =1，δi,kold(t - 1) - =1，以及δi,knew(t - 1) + =1，其中，kold= zij(t - 1)且 knew= zij(t - 1)～ P(zij|xij, δi(t - 1), B(t - 1))。这些方程产生不同单词记号wij和 wuν之间的依存关系。其中一个明显的依存关系出现在wij= wuν，导致了它们将更新与B相同要素的可能(这发生在kold或knew对于两个记号相同时)。此外，在条件概率P(zij|xij, δi(t - 1), B (t - 1))中还有更复杂的依存关系，为了使本文保持在一个适当的高度，我们可以总结指出元素在列B·,ν中是相互依存的，而在δ行即δi,·要素，也是互相依存的。由于这些错综复杂的依赖关系，高性能并行LDA主题模型需要同步数据和模型并行策略(图2)，其中，单词记号wij必须由其值ν = wij和文件i仔细分组，以避免违反在B和δ中列/行的依存关系[25]。

(2)机器学习程序中的调度。根据这些依存关系，我们如何在尽可能避免违反依存结构(注意由于机器学习的容错性，我们并非必须避免所有的依存关系)的程度上调度更新Δ——然而同时，难道由于缺乏任务或负荷的不平衡就不留下任何的P执行器机器闲置吗？这两种考虑会对机器学习程序执行时间有不同但互补的影响：避免违反依存关系，防止每次机器学习程序的迭代相比于顺序执行的降级(即该程序将不需要更多的迭代收敛)，而保持执行器机器完全从事有用的计算，能够确保来自P机器的迭代吞吐量(每秒执行的迭代)是单一机器的接近P倍。总之，近乎完美的P次机器学习加速来自于将每次迭代(相当于顺序执行)近乎理想的进程与近乎理想的迭代吞吐量(P倍顺序执行)结合起来。因此，我们希望有一个达到这两个目标的理想的机器学习调度策略。

为了解释理想化的调度是如何实现的，我们回到运行套索和LDA的例子。在套索例子中，Aj和Ak这两个参数相互依存的程度是由在第j个和第k个特征维度之间的相关性影响——我们把这个和其他类似的操作称作一种依存关系的检查。对于一个小的阈值κ，如果＜ κ，那么Aj和Ak会彼此影响不大。因此，理想的调度策略是找到所有满足＜ κ的参数对(j, k)，之后划分参数指标j∈{1,..., m}为独立子集A1, A2,...——其中，Aa和Ab两个亚子集被认为是独立的，如果任何j∈Aa而任何k∈Ab，我们就会有＜ κ。这些子集A之后可以被安全地分配到并行执行器机器(图3)，而每台机器将顺序更新参数j∈A(这样防止违反依存关系)[39]。

至于LDA，仔细审视可以发现，对于单词记号wij[方程(8)]，更新方程ΔLDA可能触及列B·,wij的任何要素以及行δi,·的任何要素。为了防止并行执行器机器在同一行/列B和δ上操作，我们必须将单词{1,..., V}的空间(对应列B)划分至P子集V1,..., VP，也要划分文件{1,..., N}的空间(对应行δ)至P子集D1,…, DP。我们现在可以进行理想的数据和模型并行化如下：首先，我们把文件子集Dp从P机器中分配至p机器；然后，每台机器只有吉布斯采样单词记号wij，使得i∈Dp,wij∈Vp。一旦所有的机器完成工作，它们彼此轮换单词子集Vp，从而p机器现在可以吉布斯采样wij，使得i∈Dp，wij∈Vp+1(或对于P机器，wij∈V1)。这个过程一直持续到P次轮换完成，此时迭代完成(每个单词记号已采样)[25]。图2说明了这个过程。

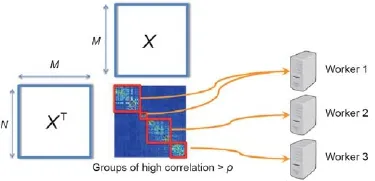
图3.理想的套索调度图解，其中的参数对(j, k)被分为子集(红色块)且不同子集中参数之间的相关性低。多个子集可以被多执行器机器并行更新，这就避免了违反依存结构，因为执行器顺序更新每个子集中的参数。

在实践中，如以上所描述的理想的调度可能并不切实可行。例如，在套索中，为所有O(m2) 对(j, k)进行的计算对于有较大m(数百万到数十亿)的高维问题十分棘手。在介绍感知结构的并行化(SAP)——一种可以被快速计算的接近理想的可行调度策略时，我们很快就会回到这个问题。

(3)机器学习程序中的计算优先化。因为机器学习程序表现出非均匀参数收敛，一个机器学习调度器就有机会优先慢收敛参数Aj，从而促进机器学习算法的每次迭代过程(即因为它需要更少的迭代收敛)。例如，在套索中，经验观察到稀疏性诱导的l1范数[方程(4)]使大多数参数Aj几次迭代后完全变为零，而之后它们不太可能再变为非0。剩下的参数，通常是一小部分，则需要更长时间来收敛(如超过10倍的迭代)[39]。

一个通用但有效的优化策略是以其平方变化率的概率比例[Aj(t - 1) - Aj(t - 2)2+ ε，其中，ε是一个保证固定参数仍有机会被选择到的很小的常数]来选择参数Aj。根据快收敛和慢收敛参数的比例，此优化策略可以导致套索回归需要进行的收敛次数呈数量级地减少[39]。类似的策略已经应用到另一个迭代收敛算法PageRank中[53]。

(4)在机器学习程序中平衡工作负荷。在用分布式集群执行机器学习程序时，为了交换参数更新，它们可能不得不停止，即同步——例如，在Hadoop和Spark中的Map和Reduce阶段结束时。为了减少花在等待上的时间，对每台机器上的工作进行负荷平衡是可取的，以使得它们继续以接近相同的速度推进。这对于可能会出现扭曲的数据分布的机器学习程序尤其重要；例如，在LDA主题模型中，单词记号wij以幂律方式分布，其中一些单词会出现在许多文件里，而其他大多数单词会很少出现。一个典型的机器学习负荷均衡策略可以应用在计算机科学中的经典装箱算法(每个执行器机器都是要包装的“箱”之一)，或任何其他以操作为中心的分布式系统如Hadoop和Spark工作的策略。

然而，不太起眼的第二个挑战是，机器的性能可能由于微妙的原因，诸如改变数据中心温度、机械故障、背景工作或者其他用户等在实际集群中发生波动。因此，预定在一次迭代开始的负荷均衡策略，会经常遭遇落后者，即随机变得比集群的其他部分慢的机器，当一次迭代结束、运行参数同步时其他所有的机器必须等待这些机器[37,40,60]。解决这个问题的一个简单方法是应用慢速执行器的不可知论[38]，即系统直接利用机器学习算法的迭代收敛性，并允许更快的执行器在等待落后者赶上来的时候重复其更新Δ。这不仅解决了落后者的问题，甚至可以纠正不完美均衡的工作负荷。我们注意到的另一个解决方案是使用有界的异步执行(而不是同步的MapReduce式执行)，在3.2中将更详细地讨论这一方案。

(5)结构感知并行化。调度、优先次序和负荷均衡彼此互补又相互缠结；参数Aj优先级的选择会影响依存关系需要执行哪些调度，反过来，调度产生的“独立子集”可使负荷均衡问题变得更困难或更简单。这三个功能可以被组合成一个单一的编程抽象概念，作为机器学习分布式系统的一部分被实施。我们称这种抽象概念为结构感知的并行化(SAP)，其中，机器学习程序员可以指定如何：①优先处理参数来加快收敛速度；②对这些参数执行依存关系检查，并安排其至独立子集中；③在执行器机器中对独立子集进行负荷均衡。SAP提供了一个简单的MapReduce类编程接口，机器学习程序员能在接口上实现三个功能：①“调度()”，其中，一小部分参数被优先考虑，之后接触到依存关系检查；②“推()”，在执行器机器上并行执行ΔL；③“拉()”，执行F。负荷均衡是由SAP执行通过结合经典装箱算法和慢速执行器不可知论自动处理。

重要的是，SAP 调度()不单纯执行O(m2)依存关系检查；相反，一些参数A是首先通过优先考虑(当A＜＜m)而被选择。之后对A进行依存关系检查，由此产生的独立子集通过推()和拉()被更新。这样，SAP每次调度()，推()和拉()的迭代都只更新几个参数Aj，而不是完整的模型A。这个策略被证明对于一类广泛的模型并行性机器学习程序来说接近理想化。

定理1(改编自参考文献[35])：SAP接近了理想化的执行。考虑形式的目标函数是可分的，A∈Rd和f在下列意义上有 β-Lipschitz 连续梯度：

设X = [x1,...,xd]是重新表示为d个特征向量的数据样本。W.l.o.g.（不失一般性），我们假设每个特征向量xi归一化，即因此，对于所有的i和j，

假设我们想通过模型并行坐标下降尽量减少L。设Sideal()是总能提出零相关的P随机特征的Oracle(即理想化)的调度。设作为它的参数轨迹，并设为SAP调度的参数轨迹。那么，对常数C，m，L和Pˆ：

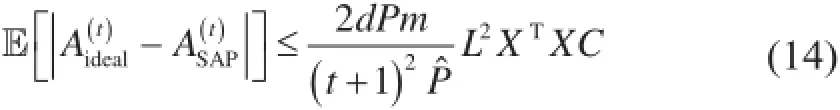
这个定理说明SSAP()参数预测ASAP与理想Oracle预测Aideal之间的差异会以一个快速的1/(t + 1)2= O(t-2) 比率迅速消失。换句话说，谁也不能做得比SSAP()调度好很多——它已经接近最优了。

SAP的慢速执行器不可知论负荷均衡还带来一种理论性能保证——它不仅保留正确的机器学习收敛，还会促进单纯调度下每次迭代的收敛。

定理2(改编自参考文献[38])：SAP慢速执行器不可知论促进了每次迭代的收敛。设模型中当前的方差(直观地说就是不确定性)是Var (A)，设np＞ 0是由执行器p进行更新的数量(包括由于慢速执行器不可知论的附加更新)。在np更新后，Var (A)降低至其中，ηt＞0，是当t→∞时接近零的步长参数；c1, c2, c3＞ 0，是特异性问题的常数；L是该机器学习目标函数L的随机梯度；CoVar(a, b)是a和b之间的协方差；O(cubic)代表迅速向零收缩的三阶或更高的项。

一个较低的方差Var (A)表明，机器学习程序接近收敛(因为参数A已经快速地停止变化)。上述定理表明，额外的更新np确实降低了方差——因此，机器学习程序的收敛得到了加速。为了理解为什么是这样的情况，我们注意到第二和第三项总是为负；此外，它们是O(ηt)，所以支配了为正的第四项[即O(并因此更快地缩小到零]以及为正的第五项(第三阶甚至比第四项收缩更快)。

根据经验，SAP系统能够在非调度、非均衡的分布式机器学习系统上实现数量级的速度提升。一个例子是转换系统[39]，它实现了多种算法的SAP调度，比如套索回归、矩阵分解，以及LDA主题模型，并且相比于其他系统实现了出色的收敛次数(图4)。

3.2.如何连接计算和通信：桥连模型和有限异步性

许多并行程序要求执行机器可以互相交换程序状态。例如，诸如Hadoop的MapReduce系统接受由所有Map(映射)执行器产生的键值对 (a, b) ，然后将所有拥有键a的键值对传给同一个Reduce(归约)执行器。对于以操作为中心的程序来说，这一步的执行必须准确无误。回想MapReduce分类的例子(第二部分)，由于键传给了不同的Reducer，结果导致了分类错误。BSP并行编程中的操作准确性这一概念由BSP模型支撑[61,62]。BSP模型是一种桥连模型，它抽象地展示了并行程序计算是如何与执行器间的通信相交错的。采用BSP桥连模型的程序在计算阶段和通信阶段或同步栅栏(synchronization barrier)(图5)间切换，且在下一个同步障碍完成前，每个计算阶段的影响对执行机器是不可见的。

由于BSP模型清楚地分离了计算阶段和通信阶段，许多在BSP下运行的并行机器学习程序是可序列化的。也就是说，它们等同于顺序机器学习程序。序列化BSP机器学习程序可以保证所有顺序队列的正确性，这使得BSP成为颇受以操作为中心的程序以及机器学习程序欢迎的桥连模型[32,34,63]。BSP的一个缺点是，执行器必须互相等待进入下一个同步栅栏。这意味着高效的BSP执行对负载均衡有严苛的要求。但是，即使是非常均衡的工作负载也会成为一些“问题机器”的牺牲品——这些机器变得比其余机器缓慢，这是随机和不可预测的[60]，是由于真实世界的一些条件，诸如数据中心的温度波动、网络拥塞以及其他用户的程序或后台任务。发生这种情况时，为了配合最慢的机器，程序的效率就会降低——而在拥有上千部机器的机群里，这样的问题机器可能有许多。第二个缺点是，执行器间的通信不是瞬时的，所以同步栅栏本身需要大量的时间。例如，LDA(Latent Dirichlet Allocation)主题模型在BSP下运行于32台机器上时，同步栅栏所需时间至多可以达到迭代的6倍[37]。由于这两个缺点，BSP机器学习程序的迭代吞吐量很低，即P台机器并不能带来P倍吞吐量的增加。

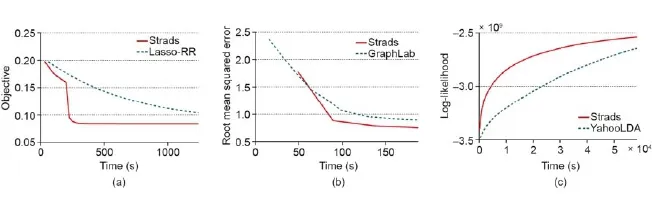
图4.三种机器学习程序目标函数L的进展的时间图表比较——(a) 套索回归(1亿条特征、9台机器)，(b) 矩阵分解(MF)(80个秩、9台机器)，(c) 隐含Dirichlet分配(LDA)主题建模(250万词汇、5 000个主题、32台机器)——在实现了结构感知并行化系统(SAP)的抽象概念的系统Strads下执行。通过使用SAP促进机器学习算法每次迭代的过程，Strads相比其他通用和专用目的的实施工具——套索-RR(又名猎枪算法)、GraphLab和YahooLDA实现了更快的收敛时间(更陡峭的曲线)。改编自参考文献[39]。

作为在BSP上运行机器学习程序的一种替代，人们又研发了异步并行执行模型(图6)[28,33,52]。在这一模型中，执行机器无需互相等待，而是在每次迭代进程中交换模型信息。异步执行可以获得近乎理想的P倍吞吐量增加。但是和BSP(能够确保可序列化性以及机器学习程序准确性)不同，异步并行每个迭代的收敛进程会减弱。原因是异步通信会使模型信息变得延后或过时(因为机器不需要互相等待)，这反过来会造成Δ和F计算的错误。错误的大小随信息的延后而增加。如果不仔细约束这些延迟，会导致收敛极其缓慢，甚至错误[37,40]。在某种意义上，没有“免费的午餐”——模型信息的通信必须在执行器间及时进行。

BSP和异步执行在实现理想化的P倍机器学习程序加速中面临着不同的挑战——从经验出发，BSP机器学习程序难以实现理想化的P倍迭代吞吐量增加，而异步机器学习程序则很难保持顺序机器学习程序中每个迭代的理想化进程[25,37,40]。有限异步执行有望解决这一问题，在该模型中异步执行被加以限制。为了更好地探索这一想法，我们展示了一种在BSP基础上提升而来的桥连模型，称为“过时同步并行”(stale synchronous parallel / SSP)[37,64]。

图5.整体同步并行(bulk synchronous parallel, BSP)桥连模型。在机器学习程序中，执行机器等在每次迭代结束时，在同步栅栏阶段中交换参数A的信息。

图6.异步并行执行模型。运行机器学习程序的机器无需互相等待。模型参数Aj的信息交换在执行器间异步持续进行。由于执行器无需等待，所以存在一个风险，即某台机器可能多次迭代、结束得比其他机器缓慢，这可能会给机器学习程序带来不可恢复的错误。而BSP系统由于其同步栅栏而不会发生这种情况。

过时同步并行(SSP)是一种有限异步桥连模型，它拥有与常见的BSP桥连模型相似的编程接口。一个直观高端的阐释如下：我们有P个并行执行器或机器以迭代的方式进行机器学习计算Δ和F。在每次迭代t结束时，SSP 执行器发出信号告知它们已完成迭代。在这一节点上，如果执行器是在BSP下运行，同步栅栏就会启动进行机器间的通信。但是，SSP则不会发生同步栅栏，而是以其认为合适的方式选择停止或允许执行器继续进行下去；更具体地说，如果该执行器有多于s个迭代先于其他执行器，SSP就会停止它，这个s称为过时阀值(staleness threshold)(图7)。

更正式一点的说法是，在SSP下，每个执行机器都有一个迭代计数t和模型参数A的本地视图。SSP执行机器“提交”它们的更新Δ，然后调用一个clock() 函数，该函数：① 发出信号告知迭代已结束，② 增加迭代计数t，③通知SSP系统将Δ信息传送给其他机器，这样它们就可以更新关于A的本地视图。这个clock() 和BSP的同步栅栏类似，不同的是，来自一个执行器的更新不需要立即传递给其他执行器——这就使执行器即使只收到更新的部分子集，也可以继续工作。这意味着，如果一些更新尚未接收，A的本地视图可能变得过时。给定一个用户选择的过时阀值s ≥ 0，SSP实现或系统至少会强制执行以下有限过时条件：

(1) 有限clock差值：最慢的执行器和最快的执行器之间的迭代计数差值必须≤ s，否则SSP会强制最快的执行器等最慢的执行器赶上来。

(2) 加上时间戳记的更新：每次迭代结束时t[就在调用clock()前]，每个执行器提交一个更新Δ，该更新用时间戳记t进行标记。

图7.过时同步并行(SSP)桥连模型。和BSP相比，运行机器学习语言的执行机器可以互相领先，直至相隔s个迭代(这里s被称为过时阈值)。领先太多的执行器会被强制停止，直到落后的执行器赶上来。和异步并行执行模型一样，模型参数Aj的信息交换在执行器间异步持续进行(加进来一些附加条件以保证机器学习收敛的正确性)，无需进行同步栅栏。SSP的优点是它大多数时间是像异步并行执行一样运行，但却可以根据需要停止执行器以保证机器学习执行的正确性。

(3) 模型状态保证：当一个执行器以clock t计算Δ时，保证其关于A的本地视图包含所有时间戳记≤ t - s - 1。本地视图可能包含也可能不包含其他机器时间戳记＞ t - s - 1的更新Δ。

(4) 自我写入读取：每个执行器会一直将自己的更新Δ包含进A的本地视图中。

因为最快的执行器和最慢的执行器相隔≤ s个clock，迭代t时执行器的A本地视图会包含所有时间戳记在区间[0, t - s - 1]内的执行器的更新，以及部分(也有可能没有)时间戳记在[t - s, t+ s - 1]范围的更新。注意，SSP是BSP模型针对机器学习程序的一种严格泛化：当s = 0时，第一个范围就变成了[0, t - 1]，而第二个区间则空了，这就和一个机器学习程序的BSP执行完全一样了。

因为SSP总是会限制任意两个执行器间的最大过时值s，所以它理论上可以强有力地保证数据并行执行和模型并行执行的收敛。为此我们给出下面两个互补定理。

定理3(改编自参考文献[40])：SSP数据并行收敛定理。考虑凸目标函数L = f (A) =f (A)，其中,单个t组件ft也是凸的。在SSP下，我们通过在各个组件ft上进行数据并行SGD算法寻找一个最小值A*，过时参数为s，共P台机器。使数据并行更新为Δt∶= -ηttft(At)，其中，ηt=。在适当的条件下[ft为利普希茨连续，且有届散度D（AA′）≤F2]，我们可以获得以下收敛速度保证：

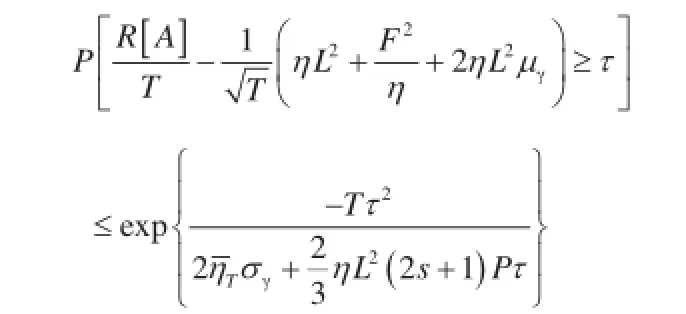
该数据并行SSP定理具有两个含义：首先，SSP下的数据并行执行是准确的(就像BSP一样)，因为R[A]/T(SSP参数的估值和实际最优值之间的差值)依指数尾界的概率收敛至O(T-1/2)；其次，重要的是要使实际过时值和异步性尽可能小，最大过时值越小，执行器经历的平均过时值μγ和过时方差σγ越小，收敛的界就越紧。由于这一原因，朴素异步系统(如Hogwild! [31] 和 YahooLDA [28])在复杂生产环境中的收敛性可能较差，机器可能由于其他的任务或用户暂时变慢，这就使最大过时值s和过时方差σγ变得任意大，进而导致较差的收敛速度。

定理4(出现于2016年)：SSP模型并行渐进相合性。考虑使用一个保持集中“全局视图”A(如在键值存储上)以及每台执行机器上的过时视图Ap的模型并行近侧梯度下降过程，来最小化目标函数L = f(A, D) + g(A)，其中，A∈Rd。如果下降步长满足η ＜ 1/(Lf+ 2Ls)，则全局视图A和本地视图Ap满足：

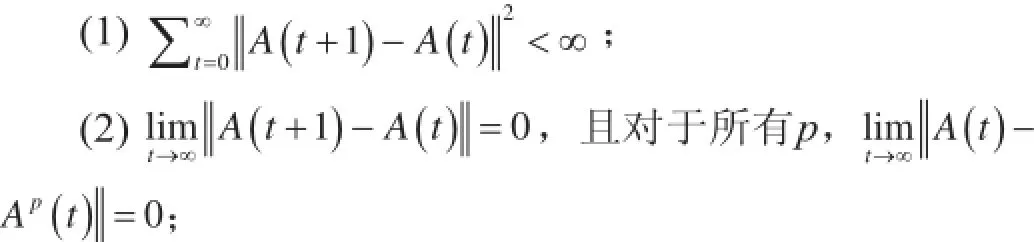
(3) {A(t)}的极限点和{Ap(t)}极限点一致，且两者都是L的临界点。

(1)和(2)意味着全局视图A会逐渐停止改变(即会收敛)，过时本地执行器视图Ap会收敛至全局视图；换句话说，SSP模型并行执行会终止于一个稳定的结果。(3)则进一步保证了本地和全局视图Ap(t)和A(t) 会取得L的最优解；换句话说，SSP模型并行执行输出的是正确的解决方案。若给定其他的技术条件，我们可以进一步健全，使SSP模型并行执行以速度O(t-1)收敛。

上述两个定理证明，SSP下的数据并行和模型并行机器学习程序都能够实现每次迭代近乎理想的收敛(接近BSP和顺序执行)。例如，Bösen系统[37,40,41] 利用SSP达到了相比于BSP桥连模型短十倍的收敛时间——而和异步执行不同，选取了合适过时值的SSP不会出现不收敛的情况(图8)。总之，如果能有效地执行和调节SSP，它几乎可以在两方面达到最佳：接近BSP的近乎理想的每次迭代进程，以及类似于异步执行的近乎理想的P倍迭代吞吐量，因此可以实现机器学习程序执行时间近乎理想的P倍加速。

3.3.如何通信：管理通信和拓扑

为了保证机器学习程序的正确执行，刚刚讨论的桥连模型(BSP和SSP)会在发生关于将更新Δ传递给模型参数A的机器学习计算时，进行约束。但是，在由桥连模型设定的约束内，仍然存在空间来规定如何或者以什么顺序在网络中传递更新Δ。考虑MapReduce类的例子在BSP桥连模型下运行：各Mapper需要将带有同一键值a的键值对 (a, b) 传给同一个Reducer。这可以通过二分拓扑结构进行，但也可以采用星型拓扑结构，第三组机器首先收集各个Mapper的所有键值对，然后将它们传递给各个Reducer。

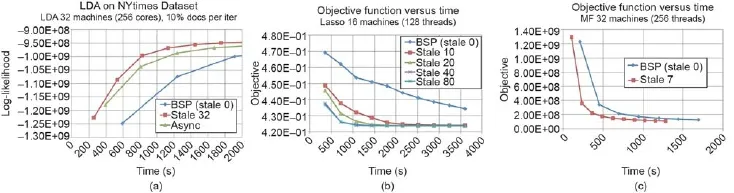
图8.三种机器学习程序下目标函数L进程和时间曲线图—— (a)LDA主题建模，(b)套索回归，(c)矩阵因子分解(MF)—— 在Bösen系统下执行，Bösen系统实现了SSP桥连模型。通过使用SSP(选取不同的过时值)提高机器学习算法的迭代吞吐量，Bösen实现了比BSP桥连模型(在Hadoop和Spark中使用)和完全异步执行模式都要快的收敛(陡峭的曲线)。尤其是，完全异步执行在套索回归和矩阵因子分解中没有成功收敛，因此没有画出它们的曲线。改编自参考文献[37]。

SSP桥连模型下的机器学习算法则具有更广阔的设计空间：因为SSP只要求更新Δ“不晚于s个迭代到达”，我们可以选择先传送更重要的更新，如果直觉告诉我们这一定可以提高每个迭代的算法进程。这些考虑是非常重要的，因为每个机组或数据中心都有它自己的物理交换机拓扑以及沿各个环节的可用带宽。选择正确的通信管理策略可以大大改善机器学习算法每次迭代的进程和提高迭代吞吐量，我们会以这一观点来讨论这些问题。现在我们来讨论几种可以将通信管理应用于分布式机器学习系统的方法。

连续通信。在SSP桥连模型的首次实现中，所有机器间的通信发生在每次迭代结束时[也就是说，在SSP clock()命令之后][37]，大多数时间下网络则是闲置的(图9)。由此产生的通信突发(千兆字节到兆兆字节)可能会引起同步延迟(如果更新到达目的地所需的时间比预期要长)，而这可以通过采用连续式通信优化掉，系统会等正在进行的更新完成传输后才开始新的更新传输[41]。

连续通信可以通过一个速度限制器在SSP过程中实现，该限制器让发送的通信列队等候，直到前面的通信完成后才将其发出。重要的是，不论该机器学习算法是数据并行还是模型并行，连续通信都仍然可以维持SSP的有限过时条件——因此，它还是会有和SSP一样的每次迭代最糟糕的收敛进程问题。此外，因为管理通信减少了同步延迟，它会略微加速(两至三倍)整个收敛时间，部分要归因于每个迭代进程的提升(延迟减少同时也意味着本地参数视图A的平均过时值降低；因此，SSP每个迭代的进程会根据定理3提升)。

免等待反向传播。机器学习模型的深度学习家族由于其高度分层结构，为连续通信提供了一个特别的机会。两个观察结果特别突出：① “反向传播”梯度下降算法——常用于训练诸如卷积神经网络(CNN)的深度学习模型——以分层模式进行；② 典型CNN(如AlexNet[20])层次的模型大小高度不对称，要求进行反向传播计算——通常，顶部完全连接层有大约90%的参数，底部卷积层负责90%的反向传播计算[56]。这就允许了一个特殊类型的连续通信，我们将其称作免等待反向传播：在顶层执行完反向传播后，系统会在执行底部反向传播时传递参数。这使计算和通信以最优的方式展开，本质上就是“90%的计算和90%的通信重叠”。

图9.整个计算过程中，SSP下的管理通信均匀地分布在网络通信中，而不是在迭代边界后就马上传递所有的更新。

更新优先化。另一种通信管理策略是划分可用带宽的优先级，传递对收敛贡献最大的更新(或部分更新)Δ。这一概念与3.1节中讨论的SAP有很紧密的联系。SAP优先计算更重要的参数，而更新优先化则确保这些重要参数的改变可以很快地传播给其他执行机器，感受到它们的影响。举一个具体的例子，在使用SGD的机器学习算法(如逻辑回归和套索回归)中，目标函数L随参数Aj按比例变化，因此变化最快的参数Aj通常对求解质量贡献最大。

因此，SSP的实现可以通过一个优先器进一步增强，该优先器重新排列速度限制器中的传出队列，这样更重要的更新会首先传出。优先器可以支持下列策略。

(1) 绝对参量优先化：根据Aj最近累积的变化 |δj| 重新排列Aj，这非常适用于使用SGD的机器学习算法。

(2) 相对参量优先化：和绝对参量一样，只是排序标准是|δj|/Aj，即用实时参数值Aj标准化积累的变化|δj|。根据经验，这些优先化策略可以产生25%的加速，在SSP和连续通信之上[41]，并且仍有潜力探索出为特殊机器学习程序量身定制的策略(类似为套索设计的SAP优先化标准)。

参数存储和通信拓扑结构。第三种通信管理策略是考虑通过网络放置模型参数A(参数存储)，以及参数更新Δ的通信路径网络路由(通信拓扑结构)。参数存储的选择会大大影响可用通信拓扑结构，这反过来影响参数更新Δ在网络中传递的速度(以及过时值)。因此，我们接下来开始讨论两种常见的存储模型参数的范例(图10)。

(1) 集中存储：参数A的“全局视图”通过一组服务器进行分区存储，而执行机器则保留参数的本地视图。通信在以下意义上是不对称的：更新Δ从执行器传到服务器，执行器从服务器接收到最新版本的参数A。

(2) 分散存储：每个执行器保持自己的参数本地视图，没有一个集中的服务器。通信是对称的：执行器互相传递更新Δ，以使它们的本地视图A达到最新状态。

主从式拓扑结构可以支持集中存储式范例(图11)，机器以二分图形式排列，一边为服务器，另一边为执行器；而分散存储式范例可以通过对等(P2P)拓扑结构(图12)来支持，每个执行机器向其他执行机器进行传播。主从式网络拓扑结构的一个优势是它减少了需要通过网络被传递的信息的数量：执行器只需要将更新Δ传送给服务器，服务器使用F聚合它们，然后更新参数A的主视图。接着，更新后的参数可以作为一条单独的信息传输，而不是作为单个更新Δ的集合。总的来说，只需要传递O(P)条信息。而P2P拓扑结构每次迭代必须发送O(P2)条信息，因为每个执行器必须将Δ传递给其他所有执行器。

但是，如果δ结构紧凑或可压缩——例如，深度学习之类矩阵参数化机器学习程序中的低秩性，或者套索回归中的稀疏性——与主从拓扑结构相比，P2P拓扑结构可以大大节省通信。通过以一种更低秩或稀疏的形式压缩或再呈现Δ，O(P2)条 P2P消息中的每条消息可以变得比O(P)条主从式消息更小，因为主从式消息不允许压缩(因为消息是由实时参数A组成，而不是可压缩的更新Δ)。此外，可以通过将完全P2P转换成部分连接Halton序列拓扑结构(图13)，减少O(P2)条 P2P消息[65]，在该结构中，每个执行器只和执行器的一个子集通信。执行器可以通过经中间节点路由消息，与其他机器通信。例如，路由路径1→2→5→6是将消息从1号执行器传递至6号执行器一条路。中间节点可以将要发送至同一目的地的消息结合在一起，这样就减少了每次迭代消息的数量(并进一步减少了网络负载)。但是，Halton序列的一个缺点是，路由增加了消息到达目的地的时间，这就增大了SSP桥连模型下参数的平均过时值。例如，消息从1号执行器传递到6号执行器过时三次迭代。但是，Halton序列拓扑结构对于P2P带宽受限的大型机组网络仍然是一个非常好的选择。

通过结合“如何通信”的不同方面——连续通信，更新优先化，以及参数存储和通信拓扑结构的合理结合——我们可以设计一个拥有各方面速度优势叠加的分布式机器学习系统，获得相比SAP(如何分布)以及SSP(桥连模型)几乎是数量级的速度提升。例如，Bösen SSP系统可以获得比连续通信和更新优先化高达额外四倍的加速，如图14和图15所示[41]。 3.4.通信的对象

图10.参数存储的两种范例。注意，两种范例的通信模式不同：集中存储将更新Δ从执行器传递到服务器、实时参数A从服务器到执行器；分散存储只在执行器间传递更新Δ。

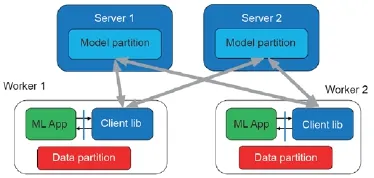
图11.集中参数存储的主从(二分)网络拓扑结构。服务器只和执行器通信，反之亦然。没有服务器间或执行器间的通信。

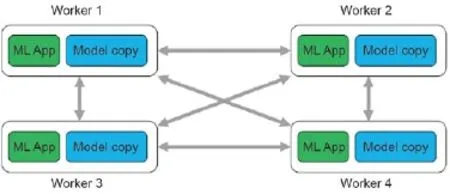
图12.分散参数存储的对等(P2P)网络拓扑结构。所有执行器与其他执行器通信。

图13.分散参数存储的Halton序列拓扑结构。执行器通过中间机器与其他执行器进行通信，例如，1号执行器可以通过将更新Δ转交给2号执行器来与5号执行器通信。

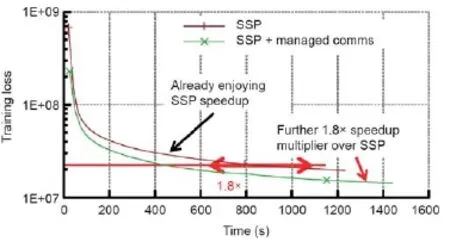
图14.矩阵分解：连续通信加SSP，其收敛时间比单用SSP提升了1.8倍。实验设置：网飞(Netflix)公司数据集，400秩，8台机器(每台16核)，千兆以太网(GbE)。改编自参考文献[41]。

图15.LDA主题模型：连续通信加SSP，其收敛时间比单用SSP提升了三倍。而且，如果同时采用更新优先化，收敛时间还能再减少25%。实验设置：NYTimes数据集，1 000个主题，16台机器(每台16核)，千兆以太网。改编自参考文献[41]。

除了在执行器机器之间如何存储和传递更新Δ，我们还会问在每次更新Δ时需要通信“什么”。尤其是有没有什么方法可以减少发送Δ需要的字节数，从而进一步缓解分布式机器学习程序中的交流瓶颈[55]？这个问题与以操作为中心的项目中无损压缩的思想有关，如Hadoop MapReduce能够压缩键值对(a，b)来降低从映射器到减速器的传输成本。对于数据并行机器学习程序，一种常用的降低Δ消息大小的策略是利用F内可加结构[就像套索数据并行的例子，方程(10)]，在网络传输前将其聚合(即总计)。这种早期的聚合是为了从服务器到执行器交流完整的参数A[37,40]的集中参数存储模式服务，我们很自然要问是否还有其他或许可以更好地适应不同存储模式的策略。

要回答这个问题，我们可以审视一下机器学习参数A的数学结构，及其更新Δ的性质。许多流行的机器学习程序都有矩阵结构的参数A(我们使用传统的粗体字以区别于一般的A)。例子包括多类Logistic回归(MLR)、神经网络(NN)[60]、距离度量学习(DML)[66]，以及稀疏编码[23]。我们把这些称为矩阵参数化模型(MPMS)，要注意A在目前的应用可以是非常大的：在一个MLR对维基百科的应用中[67]，A是一个包含数十亿条目(几十兆字节)的325K-by-10K矩阵。值得指出的是，典型的计算机集群网络最多可以在两台机器间每秒传送几个字节；因此，这样单纯不同步的矩阵A及其更新Δ就不是瞬时性的。由于参数同步在一个迭代收敛的机器学习程序的寿命中会发生很多次，同步所需的时间就可以成为一个巨大的瓶颈。

更正式地说，MPM是一种特殊形式的机器学习目标函数如下：

其中，模型参数是一个K-by-D矩阵A∈RK×D；每个损失函数fi被定义在A上，数据取样为。具体来说， fi必须取决于结果Aui(而不是单独地由A或ui决定)。r(A)是一种像正则化矩阵一样的结构诱导函数。方程(16)一个著名的例子就是MLR，用于涉及成千上万种类K(如网络数据的集合，像维基百科)的分类问题。在MLR中，A是权重系数矩阵，ui是数据样本i的D维特征向量，vi是一个表示数据样本i的类标签的K维特征向量，损失函数fi由一个交叉熵误差函数和一个Aui的Soft-Max映射组成。MPM的一个关键性质是，每个更新Δ是一个低秩矩阵，可分解成被称为充分因素的小的向量，通过网络发送较为便宜。

充足因素传播(SFB)。为了利用MPM充足因素的性质，让我们仔细观察更新Δ。机器学习目标函数方程 (16)还可以通过随机梯度下降(SPGD)[37,52,60,65]或随机双坐标上升(SDCA)[68-72]算法技术解决。例如，在SPGD中，更新函数Δ可以被分解为向量 biciT的总和，其中，ci= ui；SDCA更新Δ也允许类似的分解[55]。作为发送(总大小KD)的代替，我们可以发送个别矢量bi和ci[总大小S(K + D)]，其中S是样本数据在当前迭代处理的数量)，并在目标机上重建Δ。

这种充足因素传播(SFB)策略适合于分散式存储模式，其中，只有更新Δ是在执行器之间传播。它也可以被应用到集中存储的模式，不过只用于从执行器到服务器的传输；服务器到执行器的工作方向发送不再具有充足因素属性的完整矩阵A[60]。在这一点上，我们很自然要问分散存储和SFB的组合如何与SSP桥连模型相互作用，机器学习算法仍然会在这样的P2P设定下输出正确的答案吗？下面的定理提供了一个肯定的答案。

定理5(改编自参考文献[55])：在SSP下的SFB收敛定理。设对于在与过时的s连接的SSP模型下被SFB解决的方程(16)中的机器学习目标函数L(假设r ≡ 0)，Ap(t), p = 1,…, P, A(t)分别是本地执行器视图和一个“参考”视图。在温和的假设下，我们有

直观地说，定理5表明本地执行器视图Ap(t)最终收敛到目标函数L的稳定点(局部极小值)，即使更新Δ在高达s次迭代后是过时的。因此，分散式存储下SFB在SSP桥连模型下是稳健的——对于比如Halton序列的加快了更新过时速度以交换较低带宽的拓扑结构尤其有效。

根据经验，SFB可以大大降低MPM的通信成本：图16显示了对于各种MPM使用BSP桥连模型达到一个固定函数值所花费的时间。在SFB下运行的MPM要比在发送全面更新Δ(称为“全矩阵同步”或FMS)的集中式存储模式下运行收敛更快。我们也把在SFB下运行的MPM比作包括Spark v1.3.1的基线的实现(不是所有被评估的MPM都可在Spark上使用)。这是因为SFB具有更低的通信成本，所以更大比例的算法运行时间就花在了计算而不是网络等候上。我们用图17表示，图上绘制了在BSP一致性和不同Minibatch大小下，MLR每秒处理的数据样本(即迭代吞吐量)和每个样本的算法处理(即每次迭代的处理)。图17(b)显示SFB每秒处理的样本比FMS会多很多，而图17(c)显示SFB和FMS在BSP下每个样本得到完全相同的算法处理。

要了解SFB在Δ通信成本上的影响，让我们看看图18，显示了在一系列的SSP过时值上的总计算时间以及SFB和FMS收敛所需的网络通信时间。一般来说，更高的Δ通信成本和较少的过时会增加机器学习程序花在等待网络通信上的时间。对于所有的过时值，SFB需要更少的网络等待(因为SFB比FMS中的全矩阵要小得多)。SFB的计算时间比FMS略长，因为：①更新矩阵Δ必须在每一个执行器上重建，以及②SFB比起FMS需要更多的迭代来进行收敛，这是因为相比于FMS，SFB参数过时平均值稍高。总的来说，SFB在网络等待上减少的时间远远超过增加的计算时间，因此SFB胜过了FMS。

图16.(a)多类Logistic回归(MLR)、(b)距离度量学习(DML)和(c)L2- MLR的收敛时间与模型大小对照。

图17.(a)MLR任务与运行时间对照；(b)样本与运行时间对照；(c)任务与样本对照。

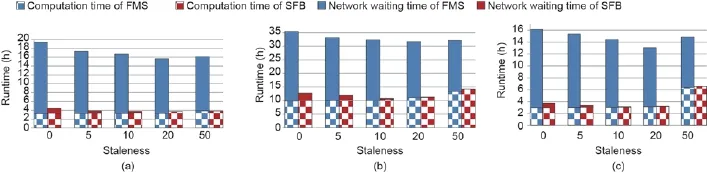
图18.计算时间与网络等待时间对照：(a) MLR；(b) DML； (c) L2- MLR。

最后一点，有些情况自然要求SFB和完整Δ传送的混合。一个很好的例子是使用卷积神经网络的深度学习(先前在3.3节中讨论了免等待反向传播的话题)：一个典型CNN的顶层被完全连接起来，使用了包含数百万要素的矩阵参数，而底层是卷积的，并涉及至多几百个要素的小矩阵。由此得出结论，应用SFB到顶层的更新[传输成本为S(K + D)KD，因为K和D很大程度上与S相关]、传输之前聚合(总计)底层的更新[成本为KD S(K + D)，因为S很大程度上与K和D相关] [56]，这两种方法都会更加有效。

4.Petuum：一种机器学习系统设计原则的实现方式

我们通过指出机器学习系统设计的四条原则已经由一些高度专用于一个或多个机器学习程序的系统部分实现，来对本文做出总结[28,31,36,58,60]。这就为机器学习从业人员提供了在上述的专、精但高性能的“塔”(需要大量的工程作业以进行维护、升级的专业化系统)，与更通用但速度也更慢的“平台”，如Hadoop和Spark(相对易于部署和维护)之间的选择。为了解决这种对立，我们已经得出了机器学习系统设计在Petuum分布式机器学习框架[35]中的原则，其结构如图19所示。Petuum蕴含的目的是为进行大数据运算的机器学习算法提供一种通用的分布式系统，通过从ML程序员那里提取系统的实施细节和设计的四个原则，ML程序员得到释放之后可以专注于对机器学习的关键函数L、Δ和F进行编程。

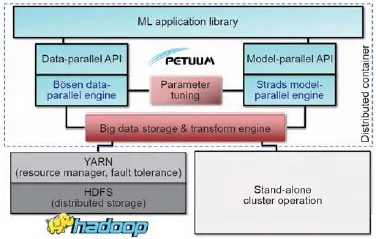
图19.Petuum结构，一种为大数据和大模型工作的分布式机器学习系统。

相比于对于以操作为中心的程序通用的分布式编程平台(如Hadoop和Spark)，Petuum利用迭代收敛机器学习程序的独特性能——容错性、依存结构、非一致收敛、紧凑更新——以提高机器学习算法的收敛速度和每次迭代的时间，从而用P台机器实现接近理想化的P倍加速。Petuum运行集群计算和云计算，以几十到数千台机器进行支持，并提供C++和Java的编程接口，同时也支持另一种资源协调者(YARN)和Hadoop分布式文件系统(HDFS)在现有的Hadoop集群上执行。Petuum的基础为以下两大系统(图 19)。

(1)Bösen，一种为数据并行机器学习编程服务的有限异步分布式关键值存储。Bösen使用SSP一致性模型，它提供优于MapReduce的异步类性能和整体同步执行，也并不牺牲机器学习算法的准确性。

(2)Strads，一种为模型并行机器学习编程服务的动态调度。Strads进行细粒度的机器学习更新操作调度，优先计算机器学习程序中最需要计算的部分，同时避免可能会导致ML程序不收敛的危险的并行操作。

目前，Petuum描画出了一个含有超过10种随时可以运行的算法的机器学习库(在Bösen和Strads之上实现)，包括经典算法诸如Logistic回归、K-均值、随机森林，以及更新颖的算法，比如监督学习的主题模型(MedLDA)、深度学习、距离度量学习以及稀疏编码。尤其是Petuum深度学习系统Poseidon[56]，充分体现了Petuum“平台”的性质：Poseidon以有效但单机的Caffe项目①http://caff e.berkeleyvision.org/，并通过用Bösen分布式关键值存储的分布式共享内存编程接口来更换在Caffe中的内存访问例程，把它变成一个分布式图形处理单元(GPU)系统。这个平台方式最大的好处是熟悉性和可用性——现有的Caffe用户不必为了利用GPU在整个集群中的分布就要学习一个新的工具。

展望未来，我们想象Petuum可能会成为为机器学习应用程序用户或程序员提供单机或笔记本电脑类经验的机器学习分布式集群操作系统的基础，同时充分利用由成千上万的机器的数据中心规模的集群所提供的计算能力。要实现这一愿景，肯定还需要开发新的系统，比如集装箱化、集群资源管理和调度，以及待开发的用户界面，这些都是减少数据中心环境中大规模应用的大量的人力或运营成本部署的必要步骤。通过在以机器学习为中心的Petuum平台上建立这样的系统——使其能够用更少的机器运行得更快，以降低机器学习应用的资本成本——我们可以因此准备好将最终的大数据计算从数据库风格的操作转变为机器学习风格的操作。

Compliance with ethics guidelines

Eric P.Xing, Qirong Ho, Pengtao Xie, and Dai Wei declare that they have no conflict of interest or financial conflicts to disclose.

[1] Airoldi EM, Blei DM, Fienberg SE, Xing EP.Mixed membership stochastic blockmodels. J Mach Learn Res 2008;9:1981-2014.

[2] Ahmed A, Ho Q, Eisenstein J, Xing EP, Smola AJ, Teo CH.U nified analysis of streaming news.In: Proceedings of the 20th International Conference on World Wide Web; 2011 Mar 28-Apr 1; Hyderabad, India; 2011.p.267-76.

[3] Zhao B, Xing EP.Qua si real-time summarization for consumer videos.In: Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2014 Jun 23-28; Columbus, OH, USA; 2014.p.2513-20.

[4] Lee S, Xing EP.Leve raging input and output structures for joint mapping of epistatic and marginal eQTLs.Bioinformatics 2012;28(12):i137-46.

[5] Thrun S, Montemerlo M, Dahlkamp H, Stavens D, Aron A, Diebel J, et al.Stanle y: the robot that won the DARPA Grand Challenge.J Field Robot 2006;23(9):661-92.

[6] Chandola V, Banerjee A, Kumar V.Anomaly detection: a survey.ACM Comput Surv 2009;41(3):15:1-15:58.

[7] Wainwright MJ, Jordan MI.Graphica l models, exponential families, and variational inference.Hanover: Now Publishers Inc.; 2008.

[8] Koller D, Friedman N.Probabil istic graphical models: principles and techniques.Cambridge: MIT Press; 2009.

[9] Xing EP.Probabilistic graphical models [Internet].[cited 2016 Jan 1].Available from: https://www.cs.cmu.edu/～epxing/Class/10708/lecture.html.

[10] Zhu J, Xing EP.Maximum entropy discrimination markov networks.J Mach Learn Res 2009;10:2531-69.

[11] Zhu J, Ahmed A, Xing EP.MedLDA: maximum margin supervised topic models for regression and classication.In: Proceedings of the 26th Annual International Conference on Machine Learning; 2009 Jun 14-18; Montreal, Canada; 2009.p.1257-64.

[12] Zhu J, Chen N, Xing EP.Bayesian i nference with posterior regularization and applications to innite latent SVMs.J Mach Learn Res 2014;15(1):1799-847.

[13] Griffiths TL, Ghahramani Z.Infinite latent feature models and the Indian buffet process.In: Weiss Y, Schölkopf B, Platt JC, editors Proceedings of the Neural Information Processing Systems 2005; 2005 Dec 5-8; Vancouver, Canada; 2005.p.475-82.

[14] Teh YW, Jordan MI, Beal MJ, Blei DM.Hierarchical d irichlet processes.J Am Stat Assoc 2006;101(476):1566-81.

[15] Yuan M, Lin Y.Model selection and estimation in regression with grouped variables.J R Stat Soc B 2006;68(1):49-67.

[16] Kim S, Xing EP.Tree-guided group lasso for multi-response regression with structured sparsity, with applications to eQTL mapping.Ann Appl Stat 2012;6(3):1095-117.

[17] Burges CJC.A tutorial on support vector machines for pattern recognition.Wires Data Min Knowl 1998;2(2):121-67.

[18] Taskar B, Guestrin C, Koller D.Max-margin Markov networks.In: Thrun S, Saul LK, Schölkopf B, editors Proceedings of the Neural Information Processing Systems 2003; 2003 Dec 8-13; Vancouver and Whistler, Canada; 2003.p.25-32.

[19] Hinton G, Deng L, Yu D, Dahl GE, Mohamed A, Jaitly N, et al.Deep neural netw orks for acoustic modeling in speech recognition: the shared views of four research groups.IEEE Signal Proc Mag 2012;29(6):82-97.

[20] Krizhevsky A, Sutskever I, Hinton GE.ImageNet classificati on with deep convolutional neural networks.In: Pereira F, Burges CJC, Bottou L, Weinberger KQ, editors Proceedings of the Neural Information Processing Systems 2012; 2012 Dec 3-8, Lake Tahoe, USA; 2012.p.1097-105.

[21] Lee DD, Seung HS.Learning the parts of o bjects by non-negative matrix factorization.Nature 1999;401(6755):788-91.

[22] Salakhutdinov R, Mnih A.Probabilistic matrix fac torization.In: Platt JC, Koller D, Singer Y, Roweis ST, editors Proceedings of the Neural Information Processing Systems 2007; 2007 Dec 3-6; Vancouver, Canada; 2007.p.1257-64.

[23] Olshausen BA, Field DJ.Sparse coding with an ov ercomplete basis set: a s trategy employed by V1? Vision Res 1997;37(23):3311-25.

[24] Lee H, Battle A, Raina R, Ng AY.Efficient sparse coding algorithms.In: Schölkopf B, Platt JC, Hoffman T, editors Proceedings of the Neural Information Processing Systems 2006; 2006 Dec 4-7; Vancouver, Canada; 2006.p.801-8.

[25] Zheng X, Kim JK, Ho Q, Xing EP.Model-parallel inference for big topic models.2014.Eprint arXiv:1411.2305.

[26] Yuan J, Gao F, Ho Q, Dai W, Wei J, Zheng X, et al.LightLDA: big topic models o n modest compute clusters.2014.Eprint arXiv:1412.1576.

[27] Coates A, Huval B, Wang T, Wu DJ, Ng AY, Catanzaro B.Deep learning with COTS HPC systems.In: Proceedings of the 30th International Conference on Machine Learning; 2013 Jun 16-21; Atlanta, GA, USA; 2013.p.1 337-45.

[28] Ahmed A, Aly M, Gonzalez J, Narayanamurthy S, Smola AJ.Scalable inference in latent variable models.In: Proceedings of the 5th International Conference on Web Search and Data Mining; 2012 Feb 8-12; Seattle, WA, USA; 2012.p.123-32.

[29] Moritz P, Nishihara R, Stoica I, Jordan MI.SparkNet: training deep network s in spark.2015.Eprint arXiv:1511.06051.

[30] Agarwal A, Duchi JC.Distributed delayed stochastic optimization.In: Shawe-Taylor J, Zemel RS, Bartlett PL, Pereira F, Weinberger KQ, editors Proceedings of the Neural Information Processing Systems 2011; 2011 Dec 12-17; Granada, Spain; 2011.p.873-81.

[31] Niu F, Recht B, Re C, Wright SJ.HOGWILD!: a lock-free approach to parallelizing stochastic gradient descent.In: Shawe-Taylor J, Zemel RS, Bartlett PL, Pereira F, Weinberger KQ, editors Proceedings of the Neural Information Processing Systems 2011; 2011 Dec 12-17; Granada, Spain; 2011.p.693-701.

[32] Dean J, Ghemawat S.MapReduce: simplified data processi ng on large clusters.Commun ACM 2008;51(1):107-13.

[33] Gonzalez JE, Low Y, Gu H, Bickson D, Guestrin C.PowerGraph: distributed graph-parallel computation on natural graphs.In: Proc eedings of the 10th USENIX Symposium on Operating Systems Design and Implementation; 2012 Oct 8-10; Hollywood, CA, USA; 2012.p.17-30.

[34] Zaharia M, Chow dhury M, Das T, Dave A, Ma J, McCauley M, et al.Resilient distributed datasets: a faul t-tolerant abstraction for in-memory cluster computing.In: Proceedings of the 9th USENIX Symposium on Networked Systems Design and Implementation; 2012 Apr 25-27; San Jose, CA, USA; 2012.p.2:1-2:14.

[35] Xing EP, Ho Q, Dai W, Kim JK, Wei J, Lee S, et al.Petuum: a new platform for distributed machine learning on big data.IEEE Trans Big Data 2015;1(2):49-67.

[36] Li M, Andersen DG, Park JW, Smola AJ, Ahmed A, Josifovski V, et al.Scaling distributed machine learning with the parameter server.In: Proceedings of the 11th USENIX Symposium on Operating Systems Design and Implementation; 2014 Oct 6-8; Broomfi eld, CO, USA; 2014.p.583-98.

[37] Ho Q, Cipar J, Cui H, Kim JK, Lee S, Gibbon s PB, et al.More effective distributed ML via a stale synchronous parallel parameter server.In: Burges CJC, Bottou L, Welling M, Ghahramani Z, Weinberger KQ, editors Proceedings of the Neural Information Processing Systems 2013; 2013 Dec 5-10; Lake Tahoe, USA; 2013.p.1223-31.

[38] Kum ar A, Beutel A, Ho Q, Xing EP.Fugue: slow-worker-agnostic distributed learning for big models on big data.In: Kaski S, Corander J, editors Proceedings of the 17th International Conference on Artificial Intelligence and Statistics (AISTATS) 2014; 2014 Apr 22-25; Reykjavik, Iceland; 2014.p.531-9.

[39] Lee S, Kim JK, Zheng X, Ho Q, Gibson GA, Xing EP.On model parallelization and scheduling strateg ies for distributed machine learning.In: Ghahramani Z, Welling M, Cortes C, Lawrence ND, Weinberger KQ, editors Proceedings of the Neural Information Processing Systems 2014; 2014 Dec 8-13; Montreal, Canada; 2014.p.2834- 42.

[40] Dai W, Kumar A, Wei J, Ho Q, Gibson G, Xing EP.High-performance distributed ML at scale through parameter server consistency models.In: Proceedings of the 29th AAAI Conference on Artificial Intelligence; 2015 Jan 25-30; Austin, TX, USA; 2015.p.79-87.

[41] Wei J, Dai W, Qiao A, Ho Q, Cui H, Ganger GR, et al.Managed communication and consistency for fast data -parallel iterative analytics.In: Proceedings of the 6th ACM Symposium on Cloud Computing; 2015 Aug 27-29; Kohala Coast, HI, USA, 2015.p.381-94.

[42] Bottou L.Large-scale machine learning with stochastic gradient descent.In: Lechevallier Y, Saporta G, editors Proceedings of COMPSTAT’2010; 2010 Aug 22-27; Paris France.New York: Springer; 2010.p.177-86.

[43] Zhou Y, Yu Y, Dai W, Liang Y, Xing EP.On convergence of model parallel proximal gradient algor ithm for stale synchronous parallel system.In: Gretton A, Robert CC, editors Proceedings of the 19th International Conference on Artificial Intellige nce and Statistics (AISTATS) 2016; 2016 May 7-11; Cadiz, Spain; 2016.p.713-22.

[44] Fercoq O, Richtárik P.Accelerated, parallel and proximal coordinate descent.SIAM J Optim 2013;25(4):1997-2023.

[45] Gilks WR.Markov Chain Monte Carlo.In: Encyclopedia of bios tatistics.2nd ed.New York: John Wiley and Sons, Inc., 2005.

[46] Tibshirani R.Regression shrinkage and selection via the lasso.J R Statist Soc B 1996;58(1):267-88.

[47] Blei DM, Ng AY, Jordan MI.Latent dirichlet allocation.J Mach Learn Res 2003;3:993-1022.

[48] Yao L, Mimno DM, McCallum A.Effcient methods for topic model inference on streaming documen t collections.In: Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2009 Jun 28-Jul 1; Paris, France; 2009.p.937-46.

[49] Dean J, Ghemawat S.MapReduce: simplified data processing on large clusters.In: Proc eedings of the 6th Conference on Symposium on Operating Systems Design & Implementation-Volume 6; 2004 Dec 6-8; San Francisco, CA, USA; 2004.p.137-50.

[50] Zhang T.Solving large scale linear prediction problems using stochastic grad ient descent algorithms.In: Proceedings of the 21st International Conference on Machine Learning; 2004 Jul 4-8; Banff , Canada; 2004.p.116.

[51] Gemulla R., Nijkamp E, Haas PJ, Sismanis Y.Large-scale matrix factorization with distributed stochastic gradien t descent.In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2011 Aug 21-24; San Diego, CA, USA; 2011.p.69-77.

[52] Dean J, Corrado G, Monga R, Chen K, Devin M, Mao M, et al.Large scale distributed deep networks.In: Pereira F, Burges CJC, Bottou L, Weinberger KQ, editors Proceedings of the Neural Information Processing Systems 2012; 2012 Dec 3-8, Lake Tahoe, USA; 2012.p.1232-40.

[53] Low Y, Gonzalez J, Kyrola A, Bickson D, Guestrin C, Hellerstein JM.GraphLab: a new framework for parallel machine learning.In: Proceedings of the 26th Conference on Uncertainty in Artificial Intelligence (UAI 2010); 2010 Jul 8-11, Catalina Island, CA, USA; 2010.

[54] Hinton GE, Salakhutdinov RR.Reducing the dimensionality of data with neural networks.Science 2006;313(5786):504-7.

[55] Xie P, Kim JK, Zhou Y, Ho Q, Kumar A, Yu Y, et al.Distributed machine learning via suffi cient factor broadcasting.2015.Epri nt arXiv:1409.5705.

[56] Zhang H, Hu Z, Wei J, Xie P, Kim G, Ho Q, et a l.Poseidon: a system architecture for effcient GPU-based deep learning on multiple machines.2015.Eprint arX-iv:1512.06216.

[57] Bradley JK, Kyrola A, Bickson D, Guestrin C.Parallel coordinate descent for L1-regularized loss minimization.In: Proce edings of the 28th International Conference on Machine Learning; 2011 Jun 28-Jul 2; Bellevue, WA, USA; 2011.

[58] Scherrer C, Tewari A, Halappanavar M, Haglin D.Feature clustering for accelerating parallel coordinate descent.In: Pereira F, Burges CJC, Bottou L, Weinberger KQ, editors Proceedings of the Neural Information Processing Systems 2012; 2012 Dec 3-8, Lake Tahoe, USA; 2012.p.28-36.

[59] Low Y, Gonzalez J, Kyrola A, Bickson D, Guestrin C, Hellerstein JM.Distributed GraphLab: a framework for machine learning and data mining in the cloud.In: Proceedings of the VLDB Endowment; 2012 Aug 27-31; Istanbul, Turkey; 2012;5(8): 716-27.

[60] Chilimbi T, Suzue Y, Apacible J, Kalyanaraman K.Project Adam: building an efficient and scalable deep learning training system. In: Proceedings of the 11th USENIX Symposium on Operating Systems Design and Implem entation; 2014 Oct 6-8; Broomfi eld, CO, USA; 2014.p.571-82.

[61] Valiant LG.A bridging model for parallel computation.Commun ACM 1990;33(8):103-11.

[62] McCo ll WF.Bulk synchronous parallel computing.In: Davy JR, Dew PM, editors Abstract machine models for highly parallel computers.Oxford: Oxford University Press; 1995.p.41-63.

[63] Malewicz G, Austern MH, Bik AJC, Dehnert JC, Horn I, Leiser N, et al.Pregel: a system for large-scale graph processing.In: Proceedings of the 2010 ACM S IGMOD International Conference on Management of Data; 2010 Jun 6-11; Indianapolis, IN, USA; 2010.p.135-46.

[64] Terry D.Replicated data consistency explained through baseball.Commun ACM 2013;56(12):82-9.

[65] Li H, Kadav A, Kruus E, Ungurean u C.MALT: distributed data- parallelism for existing ML applications.In: Proceedings of the 10th European Conference on Computer Systems; 2015 Apr 21-25; Bordeaux, France; 2015.Article No.: 3.

[66] Xing EP, Jordan MI, Russell SJ, Ng AY.Distance metric learning with application to clustering with side-information.In: Becke r S, Thrun S, Obermayer K, editors Proceedings of the Neural Information Processing Systems 2002; 2002 Dec 9-14; Vancouver, Canada; 2002.p.505-12.

[67] Partalas I, Kosmopoulos A, Baskiotis N, Artieres T, Paliouras G, Gaussier E, et al.LSHTC: A benchmark for large-scale text classification.2015.Eprint arX-iv:1503.085 81.

[68] Hsieh CJ, Chang KW, Lin CJ, Sathiya Keerthi S, Sundararajan S.A dual coordinate descent method for large-scale linear SVM.In: Proceedings of the 25th International Conference on Machine Learning; 2008 Jul 5-9; Helsinki, Finland; 2008.p.408-15.

[69] Shalev-Shwartz S, Zhang T.Stochastic dual coordinate ascent methods for regularized loss.J Mach Learn Res 2013;14(1): 567-99.

[70] Yang T.Trading computation for communication: distributed stochastic dual coordinate ascent.In: Bur ges CJC, Bottou L, Welling M, Ghahramani Z, Weinberger KQ, editors Proceedings of the Neural Information Processing Systems 2013; 2013 Dec 5-10; Lake Tahoe, USA; 2013.p.629-37.

[71] Jaggi M, Smith V, Takac M, Terhorst J, Krishnan S, Hofmann T, et al.Communication-efficient distributed dual coordinate ascent.In: Ghahramani Z, Welling M, Cortes C, Lawrence ND, Weinberger KQ, editors Proceedings of the Neural Information Processing Systems 2014; 2014 Dec 8-13; Montreal, Canada; 2014.p.3068-76.

[72] Hsieh CJ, Yu HF, Dhillon IS.PASSCoDe: parallel asynchronous stochastic dual co-ordinate descent.In: Bach F, Blei D, editors Proceedings of the 32nd International Conference on Machine Learning; 2015 Jul 6-11; Lille, France; 2015.p.2370-9.

* Corresponding author.

E-mail address: epxing@cs.cmu.edu

2095-8099/© 2016 THE AUTHORS.Published by Elsevier LTD on behalf of Chinese Academy of Engineering and Higher Education Press Limited Company.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

英文原文: Engineering 2016, 2(2): 179-195

Eric P Xing, Qirong Ho, Dai Wei, Pengtao Xie.Strategies a nd principles of distributed machine learning on big data.Engineering,

http://dx.doi.org/10.1016/J.ENG.2016.02.008