具有N策略和负顾客反馈抢占型排队系统状态空间的完备性分析

周学良

（新疆工业职业技术学院，新疆 乌鲁木齐 830022）

具有N策略和负顾客反馈抢占型排队系统状态空间的完备性分析

周学良

（新疆工业职业技术学院，新疆 乌鲁木齐 830022）

将N策略与具有反馈抢占、负顾客到达的、重试这些服务规则结合在一起，然后运用补充变量方法描述具有N策略和负顾客的反馈抢占型M/G/1重试可修排队系统模型。在此基础上，研究具有N策略和负顾客的反馈抢占型M/G/1重试可修排队系统的状态空间和共轭空间的完备性。

反馈抢占型；排队系统；Banach空间；共轭空间

1 重试可修排队系统模型研究现状

在具有多通路的远程通信网络系统中，由于网络信号强弱的原因，客户端的数据传输就有可能出现中止、错误等现象，这就需要等待数据的再次传输。有关学者研究了具有反馈、启动失效的重试可修排队系统。然而在一些排队服务系统中，要完成一个服务可能需要选择几个阶段的服务，即被称为初步服务和主要服务。并且在进行初步服务时，顾客具有优先权可以抢占服务，但在进行主要服务时，顾客不会被优先权高德抢占。因此，吴锦标等［1］将N策略、具有反馈抢占、负顾客到达的、重试这些服务规则结合在一起，然后运用补充变量方法描述具有N策略和负顾客的反馈抢占型M/G/1重试可修排队系统模型，并且得到了该排队系统稳态解存在的充分必要条件。杜绍安等［2］对该模型进行了动态分析，他们首先引入系统的状态空间，算子和算子的定义域，将该模型转换为抽象的Cauchy问题，接着运用泛函分析中的线性算子半群理论证明了该模型存在唯一的正时间依赖解，然后当失效率函数为常数时，得到该模型时间依赖解的渐进行为。

此外，通过查阅文献资料，至今仍未发现关于此模型的其他任何结果。由于杜绍安等［2］研究中模型的状态空间涉及到Banach空间，但是没有给出具体详细的证明。本文沿用已有研究［3，4］的证明过程方法，运用泛函分析中线性算子的有关理论和知识来证明该系统状态空间的完备性。

2 主要结果

一类具有N策略和负顾客的反馈抢占型M/G/1重试可修排队模型偏微分方程组描述详见杜绍安等［2］的研究。其中，（x，t）∈［0，∞）×［0，∞）；p1（t）表示系统在时刻t处于待机状态的概率；p2（x，t）dx表示系统在时刻t正在接受初步服务的顾客已经耗去的服务时间在区间［x，x+dx）内的概率；p3（x，t）dx表示系统在时刻t正在接受主要服务的顾客已经耗去的服务时间在区间［x，x+dx）内的概率；p4（x，t）dx表示系统在时刻t正处于修理的状态，并且已经用去的服务时间在区间［x，x+dx）内的概率；用λ+表示正顾客的到达概率；用λ-表示负顾客的到达概率；用θ表示接受主要服务的概率；δ表示重试概率；α表示抢占服务的概率；μ（x）表示主要服务的失效率函数；η（x）表示初步服务的失效率函数；ψ（x）表示修理时间的失效率函数。

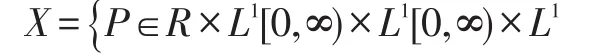
取状态空间为：

2.1 定理1——具N策略和负顾客反馈抢占型排队系统状态空间X是Banach空间

可设{gk}={pk}为空间X中的Cauchy序列，那么对，这里又因为ps-pk∈X，所以可根据状态空间中的范数定义得：

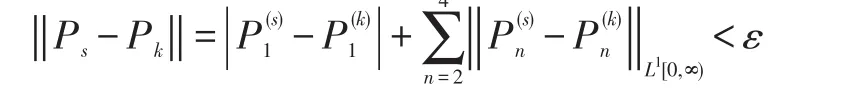
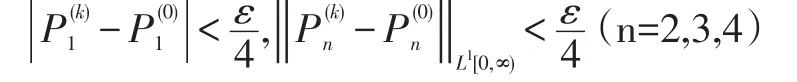
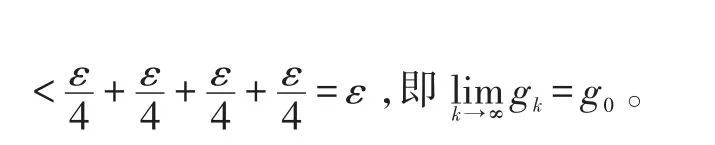
2.2 定理2——具有N策略和负顾客反馈抢占型排队系统状态空间X的对偶空间X∗是Banach空间

利用2.1同样的证明过程可以得到定理2。仍沿用杜绍安等［2］研究中的符号，且系统状态空间和对偶空间完备性的前提下，具有N策略和负顾客反馈抢占型排队系统得偏微分方程组可改写为Banach空间X中的抽象Cau⁃chy问题：

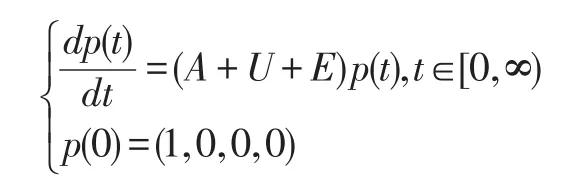
其中，线性算子A、算子U和算子E的表达式详见杜绍安等［2］研究中的符号表达，从而可以运用泛函分析中的线性算子相关理论、定理和方法进一步研究一类具有N策略和负顾客的反馈抢占型M/G/1重试可修排队系统时间依赖解的渐进行为及其他一些可靠性指标，具体研究资料方法详见周学良等［5］的证明过程。

［1］吴锦标，尹小玲，刘再明.具有N策略和负顾客的反馈抢占型M/G/1重试可修排队系统［J］.应用数学学报，2009（2）：323-335.

［2］杜绍安，艾合买提·卡斯木.具有N策略和负顾客的反馈抢占型M/G/1重试可修排队模型研究［J］.新疆大学学报（自然科学版），2010（1）：37-50.

［3］阿力木·米吉提，蔡玲霞.第二种服务可选的M/M/1排队模型状态空间及对偶空间的完备性［J］.新疆师范大学学报（自然科学版），2012（2）：72-76.

［4］周学良，吕元新.具有三种状态可修排队系统状态空间的完备性［J］.科技信息，2013（2）：133.

［5］周学良，艾尼·吾甫尔.一类具有三种状态的可修排队系统研究［J］.应用泛函分析学报，2010（2）：149-159.

Analysis of the Completeness of the State Space of Preemptive Queueing System with N Strategy and Negative Feedback

Zhou Xueliang
（Xinjiang Industrial Vocational and Technical College，Urumqi Xinjiang 830022）

The N strategy was combined with a feedback preemption,a negative customer arrival,and retry service rules,then a M/G/1 retrial repairable queueing system model with the N strategy and negative customer feedback by using the method of supplementary variable was described.On this basis,the completeness of state space and conju⁃gate space of the M/G/1 retrial repairable queueing system model with the N strategy and negative customer feedback was studied.

feedback type grab；queuing system；Banach space；conjugate space

O226

A

1003-5168（2016）09-0025-02

2016-08-25

周学良（1982-），男，硕士，讲师，研究方向：可靠性模型的动态分析。