不同浪向下脐带缆与主平台回接过程中的动力学响应

张大朋，朱克强，牛天鑫，朱艳杰，陈　凯，汤志臣，荆　彪，杨然哲

(宁波大学 海运学院，浙江 宁波315211)



不同浪向下脐带缆与主平台回接过程中的动力学响应

张大朋，朱克强*，牛天鑫，朱艳杰，陈凯，汤志臣，荆彪，杨然哲

(宁波大学 海运学院，浙江 宁波315211)

摘要:参考文昌油气田的脐带缆截面设计及具体工作环境参数，利用水动力分析软件OrcaFlex建立了文昌缆与主平台回接过程中的动力学响应模型，计算了在不同浪向下脐带缆在与主平台回接过程中的水动力响应。通过水动力分析结果可知：绞车的牵引速度和浪向的改变对脐带缆的牵拉过程有很大影响；脐带缆发生明显弯曲的部位von mises应力也会发生明显变化，但应力仍小于API 2RD的允许应力，可满足工程安全要求。

关键词:脐带缆；OrcaFlex；水动力分析；不同浪向

0引言

脐带缆是由多种功能单元螺旋缠绕组成的复合结构，用于连接上部浮式设施与水下生产系统，是海洋油气开发水下生产系统的重要装备。在安装与在位运行过程中，脐带缆在浮体运动、波浪、海流等环境因素影响下，势必受到拉伸、弯曲等荷载作用,而在脐带缆的牵拉入位操作过程中，各阶段脐带缆的张力、滑速及水中空间位形时刻在变化，且受海流及母船周围流场的影响，这些变化更加难以预测[1-3]。在此过程中，脐带缆容易被母船甲板、船身和船底缠绕或磨损，因此需要对脐带缆与主平台回接过程进行进一步的水动力分析。

本文运用国际大型水动力软件OrcaFlex建模，通过时域耦合动力分析方法计算了在不同浪向下，文昌脐带缆与主平台牵拉回接过程中的水动力响应，并结合水动力性能计算结果给出了一些指导性建议。

1项目背景及工作环境

1.1项目地点

文昌9-2/9-3/10-3油气田群位于南海西部海域。文昌9-2油气田距离海南省文昌市东海岸145 km(距岸最近距离)，距广东省湛江市区约262 km；文昌9-3油气田位于文昌9-2油气田东南约5 km处；文昌10-3油气田位于文昌9-2油气田东偏北25 km处。文昌9-2油气田所在海区水深为110～130 m，文昌9-3油气田所在海区水深约为123 m。

1.2海洋水文动力环境

工程海域潮汐类型属于不正规全日潮。各层潮流为不正规半日潮流。工程海域主浪向是NE向。百年一遇有效波高为11.6 m，最大波高为20.8 m；一年一遇有效波高为7.3 m，最大波高为12.5 m。百年一遇最大流速为2.088 m/s,十年一遇最大流速为1.500 m/s，一年一遇最大流速为1.005 m/s。全年平均风速为2.3 m/s，每年10月至次年3月以偏NE向风为主，5至8月盛行偏S向风，4月和9月为季风转换季节。常风向为NE向，频率为15%，次常年风向为ENE向和SSE向，频率分布分别为11%和10%，强风向为N向，最大风速达27 m/s，风玫瑰图如图1所示。

2脐带缆主要参数

脐带缆需要根据用户实际需求进行针对性设计[4-5]。文昌脐带缆最外层采用聚合物护套保护，其内则由多个功能构件以一定螺旋角度缠绕中心钢管组成，包括9根钢管(即图2b中标号为1～9的9根钢管)、4根电缆(即图2b中标号为10、11的电缆和填充物T1、T2之间所夹电缆及填充物T3和钢管9之间所夹电缆)及填充物(即图2b中的T1、T2和T3)。管单元具体组成为(包括中心管单元和外部管单元)：中心4根1寸管中1根为甲醇输送管，1根为液压返回管，1根为环孔管，还有1根为备用管；外部5根1/2寸管中4根为液压传动管，1根为阻垢剂输送管。电单元组成为：内部为3根铜芯导体，外部为绝缘层和填充层，其余为填充物，如图2a所示。具体尺寸如图2b所示，R表示圆钢管半径，单位为mm。

图1　工程海域风玫瑰图Fig.1　The wind rose diagram of engineering sea area

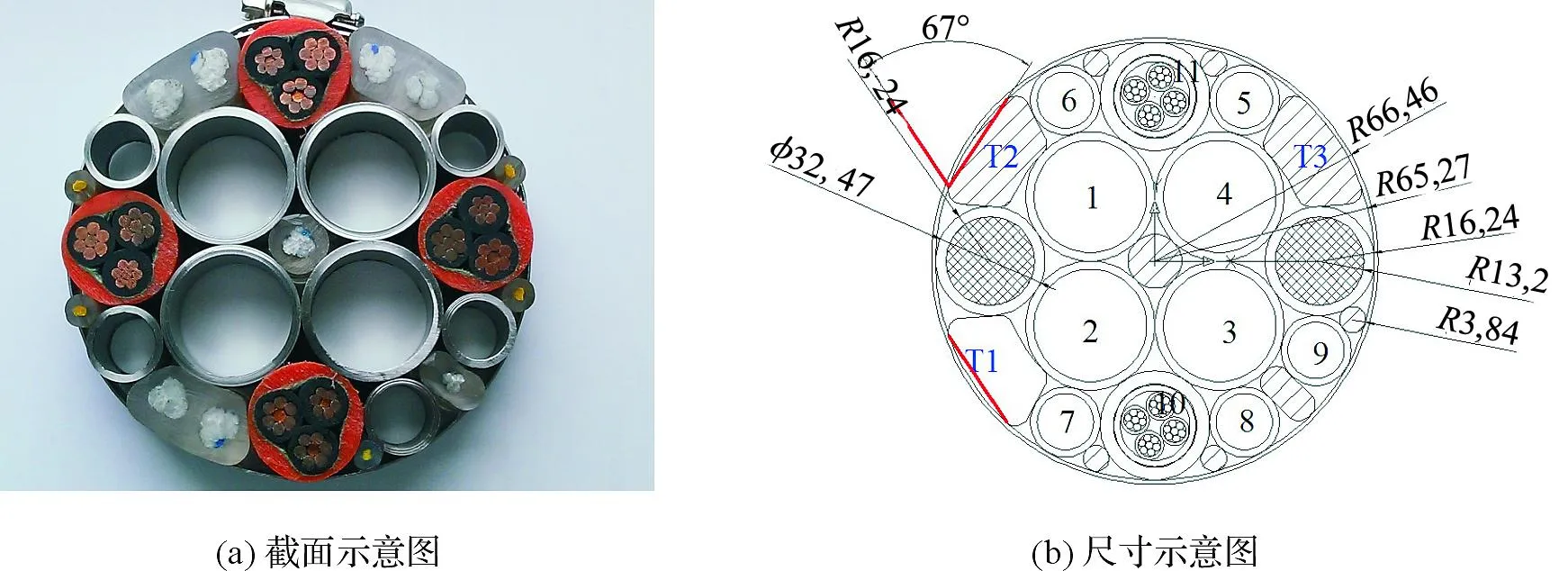
图2　文昌脐带缆截面(a)及尺寸(b)示意图Fig.2　The section(a) and size(b) of Wenchang umbilical cable cross-section

经等效计算后，脐带缆的等效弯曲刚度为14.4 kN·m2，等效轴向刚度为509 MN，扭转刚度为45 kN·m2, 最小破断力为1 067 kN。

3OrcaFlex的理论基础及基于OrcaFlex的模型建立

3.1OrcaFlex理论基础

OrcaFlex软件中坐标分为整体坐标和局部坐标，但两者均采用右手坐标系统。整体坐标的原点设在海平面上，Z轴方向垂直向上，X和Y方向满足右手定则。在画模型时，一般采用局部坐标，在确定整体模型位置时，采用整体坐标。本研究建立的模型中，平台的图形参考局部坐标给出，整个模型的位置确定参考整体坐标来确定[6]，如图3所示。

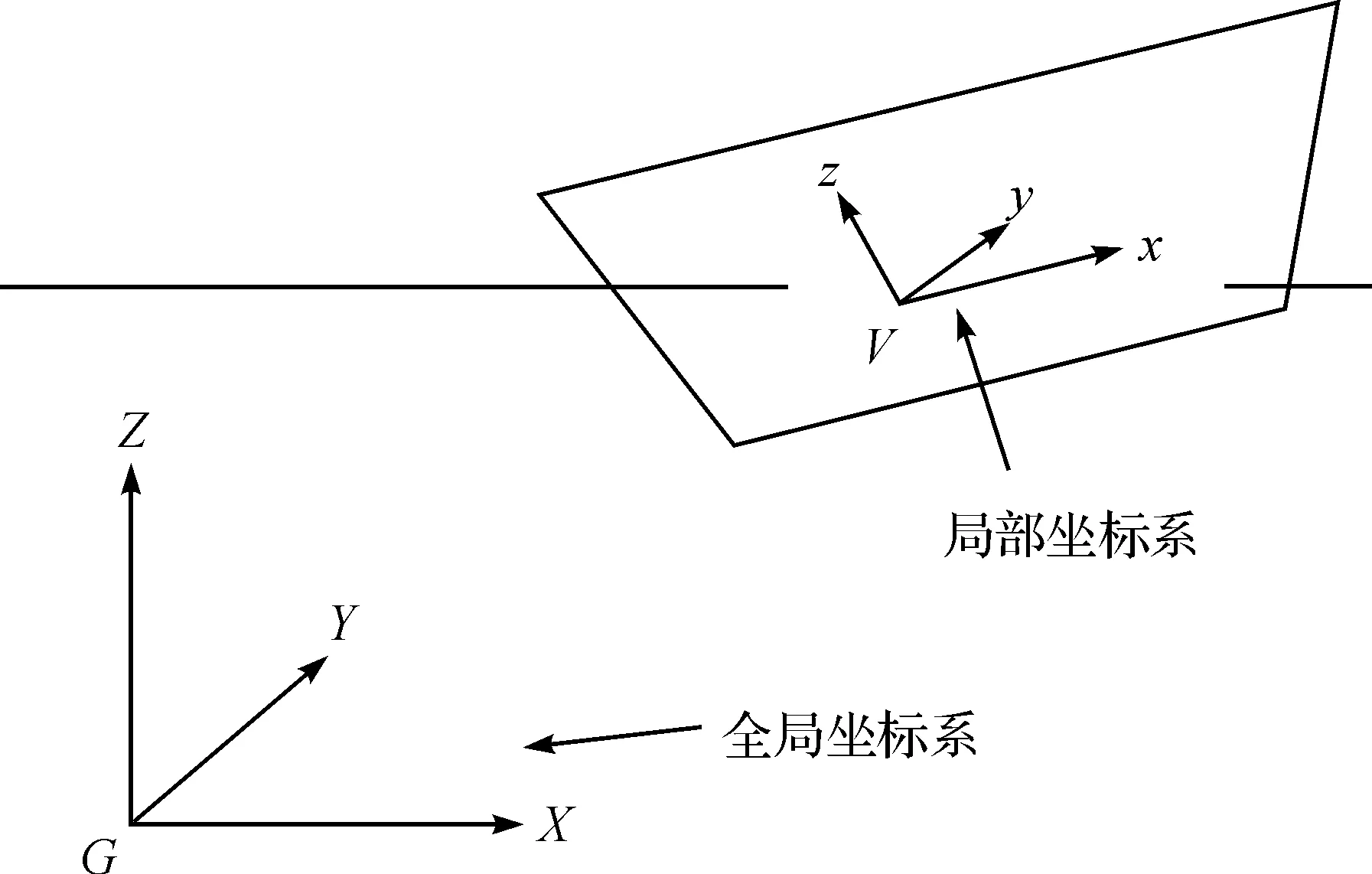
图3　全局及局部坐标系示意图Fig.3　The sketch map of global and local coordinate system

在对脐带缆进行计算分析时，假定其为挠性结构，计算分析的内容主要包括脐带缆承受的轴向张力、环境载荷作用以及整个系统的耦合动态响应。采用凝集质量法进行建模，脐带缆的性能相当于一个非线性弹簧[7]，离散为凝集质量模型[8]，由若干个连续的、无质量分段和处于各分段中点处的节点组成，将其模拟为轴向、旋转弹簧和阻尼器的组合体。节点集中了两个相邻分段各一半的质量，力和力矩都作用于节点上，这也正是OrcaFlex中对脐带缆张力建立模型的数学基础[9-10]。

对于海洋管线这类细长挠性构件，可忽略结构本身对波浪的影响，所受到的波浪力F通常用Morison公式计算。在OrcaFlex 中拓展后的Morison 公式为：

(1)

式中：Δ=ρv，为排开的水的质量，在此处ρ取为1 024 kg/m3；aw为流体对地加速度；ar为流体相对于结构物的加速度；vr为流体相对于结构物的速度；Cm为惯性力系数，CD为拖曳力系数；A为阻尼面积。Cm和CD据API (American Petroleum Institute)规范分别选取为1.2 和1.8，而波浪计算则采用线性波理论。目前波浪理论大致可以分线性波浪理论和非线性波浪理论。DEAN et al[11]指出在各种水深线性波浪理论都可以给出不错的结果，随着水深的增加，海浪基本控制方程中的非线性项的影响逐渐降低，因此本文在OrcaFlex的建模过程中选用线性波浪理论。

在OrcaFlex中脐带缆有效张力用以下公式计算：

1.2.2 肩痛穴平衡针灸治疗方式 在应用肩痛穴平衡针灸治疗方式时，主治医师需要协助患者保持坐姿，并将膝盖伸直，针灸角度选择直刺角度，并以提插的针灸手法对针进行刺入，在进行刺入操作前，需要对患者的针刺部位进行消毒处理，本次针灸治疗选择的是长度为5 cm的无菌毫针，刺入的深度为1.5寸。针灸的穴位有肩痛穴，位于人体足三里穴位的下方3寸位置处，在实际针灸过程中需要避开腓浅神经，因此要应用交叉取穴的方式，保持每10分钟行针1次的频率[4-6]。

Te=Tw+PoAo-PiAi

(2)

(3)

式中：Te表示有效张力；Po表示外部压力；Tw表示壁面张力；EA是缆轴向刚度；ε=(L-λL0)/λL0是总的轴向平均应变，λ是分段伸长系数，L0是分段原长；v是泊松比；Pi和Po分别为内、外部压力；Ai和Ao分别为脐带缆内、外部的横截面面积，对于脐带缆而言，其内部横截面积为0；e为管线阻尼系数，一般忽略不计，在本文中e取为0；dL/dt是长度增加的速率。

至于弯曲应力、曲率、von mises应力以及strouhal频率的计算在OrcaFlex中和一般教科书中的计算原理完全相同，此处不再详述。

模型的上边界限制条件主要取决于它所连接的船体的运动情况。而船体的运动取决于RAO。RAO，即Response Amplitude Operator，在船舶或者浮体设计领域，RAO是一个工程统计的概念，可以用来计算船舶在海中工作时的行为。船体RAO一般可以通过船舶的水池模型实验或者CFD计算机程序来获得。通常需要计算浮体在各种波浪情况下的船体运动，其本质是一个由波浪激励到船体运动的传递函数。在OrcaFlex中，一旦船体的RAO确定，那么船体的运动就将确定。本文根据实际船体主尺寸在OrcaFlex软件建的模型中船长为103 m，型宽为16 m，型深为13.32 m，设计吃水为6.66 m，横稳性半径为1.84 m，纵稳性半径为114 m，排水量为8 800 t，水面上正面投影为191 m2，水面上侧面投影为927 m2，方形系数CB为0.804，首摇转动惯性矩为5.83×109 kg·m2。本研究中船的RAO、波浪漂移QTFs、附加质量系数及阻尼系数的数据均来自一个103 m长的船舶在400 m水深水池的NMIWave衍射分析。

OrcaFlex整个水动力分析包括静态和动态两部分。本研究中静态分析部分主要有2个作用：(1)分析系统结构在重力、浮力和水流粘滞力作用下是否达到静态平衡；(2)为动态分析提供一个初始状态。

动态分析是从静态分析提供的稳定状态开始进行运动模拟，它包括自建阶段和模型保持分析阶段。自建阶段是波和船舶运动由0逐渐增加到所给值的阶段，这个阶段一般需要一个波长的时间。自建阶段过后，模型就可以进入保持分析阶段。动态模拟计算，采用显式和隐式两套计算方法，二者都是在每个时间步长计算系统的几何形态，充分考虑了几何非线性因素，包括波浪载荷和接触载荷等的空间变化。运动方程的求解采用定步长显式向前Euler积分，初始模型参数通过静态分析获得，计算每个自由体和节点的力和力矩，其中力和力矩包括: 重力、浮力、水动力和空气阻力、水动力附加质量、张力和剪切力、弯矩和扭矩、海底作用力及摩擦力、物体接触力、铰链和绞车施加的力等。

运动方程为：

M(p,a)+C(p,v)+K(p)=F(p,v,t)

(4)

式中：M(p,a)是系统惯性载荷，C(p,v)是系统阻尼载荷，K(p)是系统刚度载荷，F(p,v,t)是外部载荷，p是位置，v和a分别指速度和加速度，t是模拟时间长度。

3.2OrcaFlex中脐带缆与主平台回接模型的建立

脐带缆连接到重力基座或是导管架平台时，必须拉入到专用通道，该通道就是J型管。J型管一端用塞子塞紧，防止水渗入造成腐蚀。脐带缆与主平台连接时所用的J型管连接方法是：当铺管船到达平台附近时用深水遥控机器人ROV对海床和J型管入口进行可视化探查，考察J型管的物理条件和海床条件以及J型管的路线剖面。平台上的绞车牵引缆索沿着J型管下放，使其在铺管船甲板上与脐带缆的一端连好，平台上的绞车收回牵引缆索。当牵引缆索在J型管喇叭口的挡板处时，要用很大的张力才能通过。平台绞车将脐带缆拉起直到脐带缆悬挂头到达平台铺板标高处，连接于平台上控制终端。把脐带缆系统安装到船上时，脐带缆自船上垂入水中通过斜槽，斜槽是一个刚性圆弧形的支撑导向结构，以确保脐带缆在入水时的弯曲半径大于最小弯曲半径，在OrcaFlex中运用弹塑性固体模块结合实际参数来构建斜槽。在船上还有一个张紧器，对船上管线进行夹持，保持预张力。

根据具体环境参数及工作条件，在OrcaFlex中建成如图4所示模型。

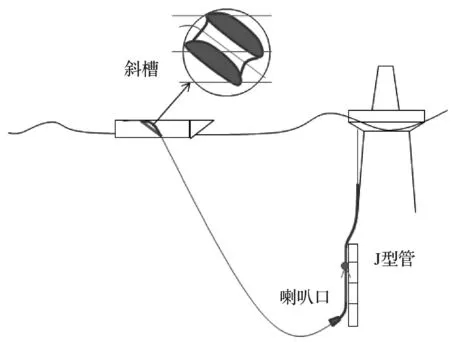
图4　文昌脐带缆与主平台回接操作示意图Fig.4　The schematic model of Wenchang umbilical cablepull-in the main platform through J-tube

4计算结果

对于管线的牵拉来说，波浪是其所承受的最重要的外部载荷，浪向的改变会使管线承受的动载荷发生很大的改变。因此，必须进行不同浪向下的动力学分析以确保整个操作过程的安全性和稳定性。为简化模型，节省计算时间，本文中暂时不考虑流载荷作用和风载荷作用。浪向取为0°～180°，每隔15°取1个浪向。在模拟过程中，船上张紧器对脐带缆的牵引点为A，即沿缆长方向长度的0 m点；水下绞车对脐带缆的牵引点为B，即沿缆长方向长度的300 m点。

4.1不同浪向下脐带缆有效张力和拉伸应变的水动力分析结果

图5为沿缆长方向脐带缆有效张力最大值、最小值和平均值的变化情况，图6为沿缆长方向拉伸应变最大值、最小值和平均值的变化情况。对比观察两幅图可知，在不同浪向时，沿缆长方向有效张力的最大值、最小值及平均值,拉伸应变的最大值、最小值及平均值在距离牵引点A 0～91 m之间除了一些有一定的斜率变化外基本各自都维持在1个近似恒定的正值(60°～120°浪向除外，此时有效张力和拉伸应变的最小值出现负值)，虽然各自有小幅度起伏，但变化不大，说明在这段缆长范围内脐带缆处于被拉伸状态。在模拟中发现，当浪向为60°～120°时，由于此时浪向接近横向浪向90°，此时波浪的作用会使船体产生大幅度的横荡和横摇，若绞车牵引速度为0.1 m/s(在0°～60°和120°～180°浪向角时绞车的牵引速度)，脐带缆在船体上的部分会产生较为剧烈的抖动和扭转，甚至会脱离船体上的牵引槽(90°浪向时)。为了使脐带缆在横浪情况下可以依然沿着斜槽较为顺利地牵引到海面以下，将绞车的牵引速度提高到了0.2 m/s，随着牵引速度的增加，单位时间内停留在船体上的脐带缆长度大大减少，降低了船体上的脐带缆发生抖动和扭转的可能性。但随着牵引速度的改变也使得这一浪向范围内，距离牵引点A 0～91 m之间的脐带缆有效张力变化情况和其他浪向时有极大的不同。由此可知，当不得不在横浪条件下施工时，可以在允许范围内增加绞车的牵引速度。

图5　沿缆长方向脐带缆有效张力变化Fig.5　The change of effective tension of the umbilical cable along the length direction

观察图5发现，有效张力的平均值和最小值均未超过脐带缆的最小破断力(1 067 kN)；在浪向为90°和105°时在距离牵引点A 225 m处出现了急剧的有效张力突变现象，此时有效张力急剧增加到一个极大值，然后沿缆长方向趋于稳定，且最大有效张力(1 600 kN和1 700 kN)均已超过了脐带缆的最小破断力，因此应该尽量避免在这两种浪向下进行施工。且经观察发现，浪向角之和为180°的2个浪向的有效张力图像形态在一定程度上呈现一定的相似性，这和理论分析的结果相一致。

图6　沿缆长方向脐带缆拉伸应变变化Fig.6　The change of direct tensile strain of the umbilical cable along the length direction

4.2不同浪向下脐带缆弯曲应力和曲率的水动力分析结果

图7为沿缆长方向脐带缆弯曲应力最大值、最小值和平均值的变化情况，图8为沿缆长方向脐带缆曲率最大值、最小值和平均值的变化情况。对比观察2幅图可知，在弯曲应力集中发生突变的地方也是曲率较大、弯曲较为严重的地方，曲率和弯曲应力的图像在形态上呈现出一定的相似性，弯曲应力突变和曲率突变发生的位置也基本相同。同时图7也说明在距离牵引点A 87.5 m处的弯曲应变和弯曲程度明显远远大于其他位置，此处的弯曲应力最大值为120 000 kPa，曲率最大值为0.75 rad/m；随着水深和缆长的继续增加，脐带缆弯曲程度开始减缓，并逐渐趋近被拉直状态；在距离牵引点A 235 m处骤然发生小幅度弯曲，随后弯曲程度迅速减缓并趋于稳定，并在脐带缆尾端被拉直，弯曲应力和曲率都变为0。且经观察发现，浪向角之和为180°的2个浪向的弯曲应力图像形态在一定程度上呈现出相似性；浪向角之和为180°的2个浪向的曲率图像形态在一定程度上也呈现出相似性，这和理论分析的结果相一致。

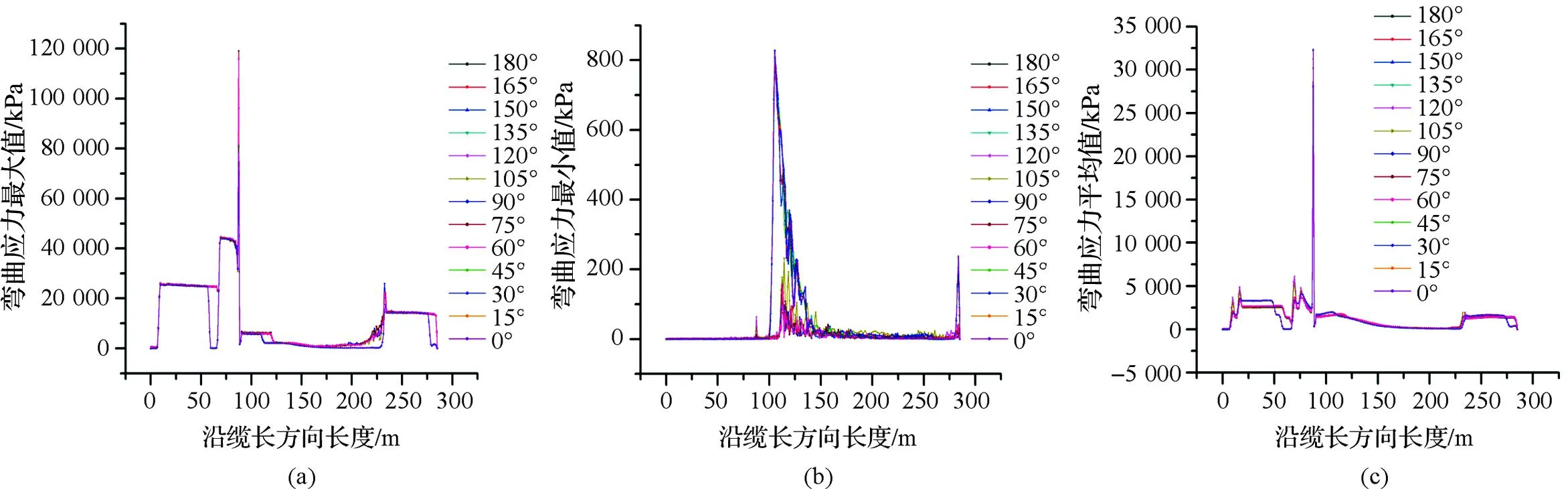
图7　沿缆长方向脐带缆弯曲应力变化Fig.7　The change of bending stress of the umbilical cable along the length direction

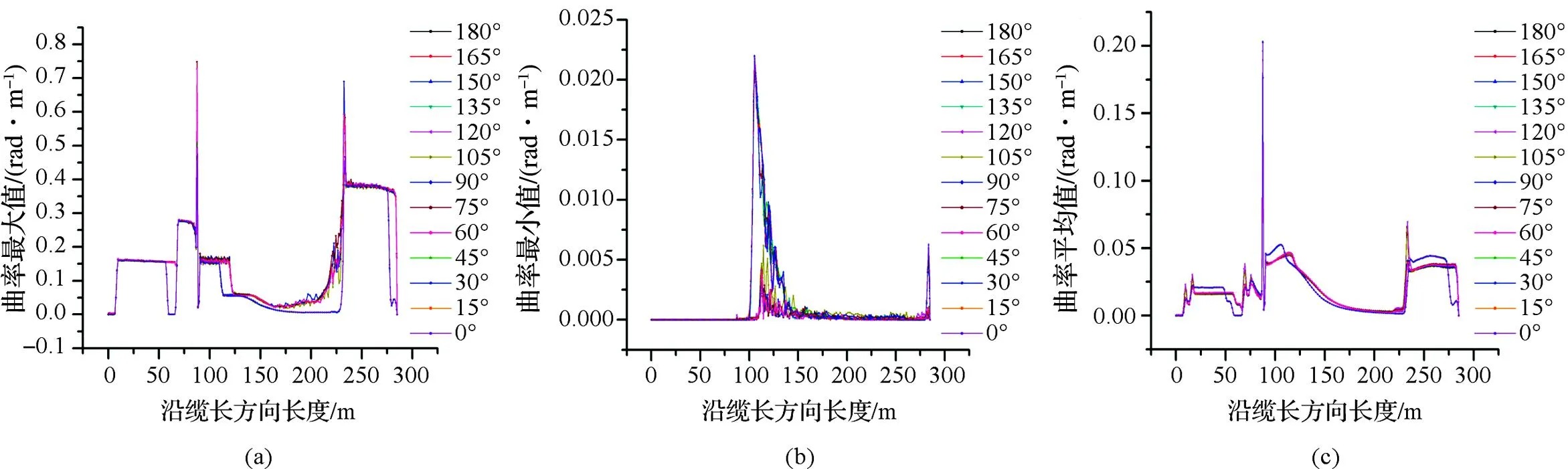
图8　沿缆长方向脐带缆曲率变化Fig.8　The change of curvature of the umbilical cable along the length direction

4.3不同浪向下脐带缆剪力的水动力分析结果

图9为沿缆长方向脐带缆剪力最大值、最小值和平均值的变化情况。由图可知，各浪向下沿缆长方向剪力的最大值和最小值及平均值在距离牵引点A 0～87.5 m之间基本为零，虽然各自有小幅度的起伏，但变化不大，说明在这段缆长范围内的脐带缆不承受剪切应力的作用。在距离牵引点A 87.5 m处会发生剪力突变现象，剪力由0急剧变为1个较大值(最大值为22.5 kN,平均值为4 kN)，然后开始沿着缆长方向降低到一个较小值(最大值为10 kN左右，平均值为1.0 kN左右)，并在距离牵引点A 87.5～122.5 m处保持不变，不同的浪向时这段区域会有小幅度的改变，但总体变化不大；随着缆长和水深的增加，在距离牵引点A 227.5 m处再次发生剪力突变现象，由较小值再次急剧增大到1个较大值(最大值为120 kN,平均值为7.5 kN)，然后再次沿缆长方向降低到一个较小值并在这个值附近发生小幅度波动直至脐带缆末端，并在脐带缆末端再次产生剪力突变，再次骤然增加。由图9b可知，沿缆长方向剪力在整条脐带缆上任意一处(脐带缆末端除外)都曾出现过为0的情况，而在脐带缆末端一直会出现剪力急剧增大的现象。这些出现剪力突变的地方也是会出现应力集中的部位，在安装的过程中应采取相关措施以便将安装过程中的损失降低到最低限度。且经观察发现，浪向角之和为180°的2个浪向的剪力图像形态在一定程度上呈现一定相似性，这和理论分析结果一致。

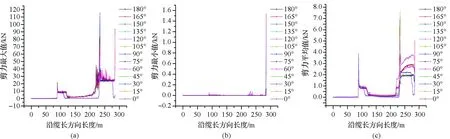
图9　沿缆长方向脐带缆剪力变化Fig.9　The change of shear force of the umbilical cable along the length direction

4.4不同浪向下脐带缆strouhal频率的水动力分析结果

图10为沿缆长方向脐带缆strouhal频率最大值、最小值和平均值的变化情况。根据strouhal频率的定义可知，在管线的直径一定时，它的数值越大，说明流体相对于管线的速度越大。通过观察图10a和图10c发现，在靠近船体部分和靠近水下绞车牵引处的脐带缆strouhal频率较大，也就是说这些部位的相对流速较大，而其他部位相对而言较小。分析产生这种现象的原因为：在靠近船体部位的脐带缆受船体运动影响较为明显，船体的运动带动脐带缆的运动使得靠近船体部位的相对流速比其他部位大；而靠近水下绞车部位的脐带缆由于水下绞车的牵引作用使得绞车附近的脐带缆的速度相对较大，也使得这一区域的相对流速较大。进一步观察发现，在距离牵引点A 87.5 m处的strouhal频率远远大于其他处，分析产生这种现象的原因为：一方面此处距离船体较近，受船体运动影响较大，使得此处的相对流速较大；另一方面，通过上文分析已知，在此处的弯曲应力和拉伸应变远大于其他部位，这也就使得此处的管线直径远比其他部位小，这两方面的原因使得此处的strouhal频率远远大于其他处。而随着水深和缆长的增加，其他部位的脐带缆运动受到水阻力影响和自身重力的影响越来越大，使得相对流速的增加变得较为困难，这也是其他部位strouhal频率较小的原因。且经观察发现，浪向角之和为180°的2个浪向的strouhal频率图像形态在一定程度上呈现一定的相似性，这和理论分析的结果一致。

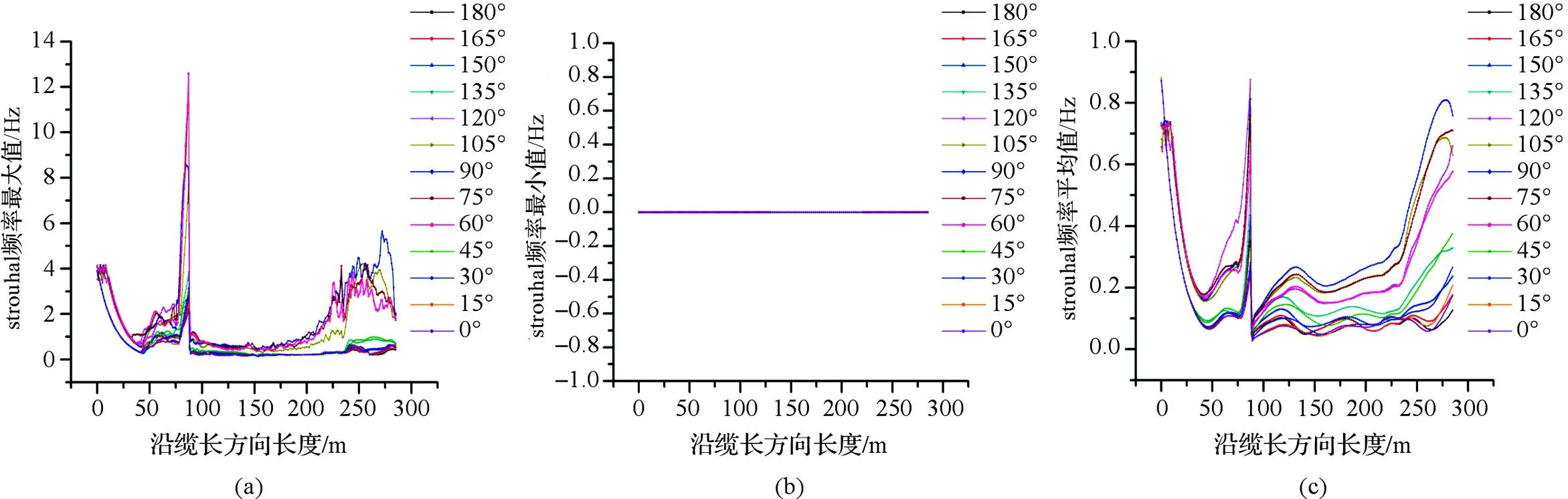
图10　沿缆长方向脐带缆strouhal频率变化Fig.10　The change of strouhal frequency of the umbilical cable along the length direction

4.5不同浪向下脐带缆von mises 应力的水动力分析结果

图11为沿缆长方向脐带缆von mises应力最大值、最小值和平均值的变化情况。由图可知，von mises应力在距离牵引点A 87.5～237.5 m处基本为0，或是在0 m附近发生小幅度波动，但总体变化不大。靠近船体的脐带缆因为受船体运动影响明显，发生了不同程度的弯扭，有明显的von mises应力变化；而在靠近水下绞车的部分脐带缆因绞车的牵引和水流的联合作用，也发生了不同程度的弯扭，但弯扭程度并没有靠近船体附近的脐带缆弯扭程度剧烈。但此时的von mises应力远小于API 2RD允许的允许应力，可满足工程要求。且经观察发现，浪向角之和为180°的2个浪向的von mises应力图像形态在一定程度上呈现一定的相似性，这和理论分析的结果相一致。

图11　沿缆长方向脐带缆von mises应力变化Fig.11　The change of von mises stress of the umbilical cable along the length direction

5结论

(1)不同浪向下，沿缆长方向有效张力和拉伸应变在距离牵引点A 0～91 m之间基本各自都维持在一个恒定的正数数值(60°～120°浪向除外，此时有效张力和拉伸应变出现负值)，虽然各自有小幅度的起伏，但变化不大，说明在这段缆长范围内脐带缆处于被拉伸状态。在浪向为60°～120°时，波浪作用会使船体产生大幅度的横荡和横摇，若绞车牵引速度为0.1 m/s(在0°～60°和120°～180°浪向角时绞车的牵引速度)，脐带缆在船体上的部分会产生较为剧烈的抖动和扭转，甚至会脱离船体上的牵引槽。且经模拟发现，在牵拉上平台的过程中脐带缆所承受的最大有效张力(特殊浪向除外)远远小于该脐带缆设计的最小破断力，能满足工程安全要求。在浪向为90°和105°时脐带缆的最大有效张力超过了该脐带缆设计的最小破断力，无法保证施工的安全，故而此时应改变船体的相对浪向或是避免在此种浪向下施工。

(2)如横浪条件下工作不可避免，可在允许范围内通过提高绞车的牵引速度，进而使得单位时间内停留在船体上的脐带缆长度大大减少，可降低船体上的脐带缆发生抖动和扭转的可能性；然而随着绞车牵引速度的增加，牵引绞车会受到较大载荷和冲击，会缩短绞车的使用寿命，也增加了脐带缆和J形管之间的磨损。

(3)由于船体运动和绞车牵引的影响，在靠近船体和水下牵引绞车的脐带缆部位相对流速较大，进而使得strouhal频率较大。另外，发生轴向拉伸和弯曲较严重部位的管线直径相对其他位置大大减小，而且这些位置离船体较近，相对流速也较大，因此这些部位的strouhal频率发生突变，远远大于其他位置。

(4)在发生明显弯扭的部位von mises应力也会发生明显的变化，但小于API 2RD的允许应力，可满足工程安全要求。

(5)浪向角之和为180°的2个浪向的水动力分析结果在一定程度上呈现相似性，这和理论分析的结果一致。

参考文献(References)：

[1] International standard13628-5 Petroleum and natural gas industries -Design and operation of subsea production system -Part 5: Subsea umbilicals [S].2002.

[2] SWANSON R C, RAO V S, VENKATARAMAN G. Metal tube umbilicals-deepwater and dynamic considerations[C]. Offshore Technology Conference. Houston, Texas, OTC 7713,1995.

[3] WILLIAMS V T, PATON K M. Malampaya deep water gas-to-power project: Subsea umbilical challenge[C]. Offshore Technology Conference. Houston, Texas,OTC 14042,2002.

[4] SAEVIK S, EKEBERG K I. Non-linear stress analysis of complex umbilical cross-sections[C]//Proceedings of 21st international conference on offshore mechanics and arctic engineering. Oslo, Norway, OMAE2002-28126,2002.

[5] SUN Jing-jing. Present situation and tendency of deepwater umbilical cable installation technology[J]. Oil Field Equipment,2011,40(12):1-5.

孙晶晶,深水脐带缆安装技术发展现状与趋势[J].石油矿场机械,2011,40(12):1-5.

[6] ORCAFLEX help file and user manual[M/OL].http://www.oricina.com.

[7] ZHU Ke-qiang, ZHENG Dao-chang, ZHOU Jiang-hua, et al. Station-keeping dynamic response of a moored production barge with multi-point mooring system[J]. Navigation of China,2007,71(2):6-9.

朱克强,郑道昌,周江华,等.生产驳船多点系泊定位动态响应[J].中国航海,2007,71(2):6-9.

[8] ZHU Ke-qiang, CAI Ying，YU Chun-ling, et al. Nonlinear hydrodynamic response of marine cable-body system undergoing random dynamic excitation[J]. Journal of Hydrodynamics,2009,21(6):851-855.

[9] YANG Bing-ka, ZHU Ke-qiang, ZHU Yan-jie, et al. Dynamic response of towed line array [J]. Journal of Hydrodynamics, Ser B,2013,25(4):616-619.

[10] ZHU Yan-jie, ZHU Ke-qiang, YANG Bing-ka, et al. Dynamics modeling and emulation technique of the marine cable considering tension and compression bending torsion deformation[J]. The Ocean Engineering,2014,32(1):112-116.

朱艳杰,朱克强,杨冰卡,等.基于凝集质量法的海洋缆索动力学建模与仿真技术[J].海洋工程,2014,32(1):112-116.

[11] DEAN R G, PERLIN M. Intercomparision of near-bottom kinematics by several wave theories and field and laboratory data [J]. Coastal Engineering,1986,9:399-437.

Dynamic response in the process of umbilical cable pull-in main platform through J-tube under different wave directions

ZHANG Da-peng, ZHU Ke-qiang*, NIU Tian-xin, ZHU Yan-jie, CHEN Kai, TANG Zhi-chen,

JING Biao, YANG Ran-zhe

(FacultyofMaritimeandTransportation,NingboUniversity,Ningbo315211,China)

Abstract:A dynamics response model are established using hydrodynamic analysis software OrcaFlex and referring to cable cross section design of Wenchang umbilical cable and operation environmental parameters to simulate the dynamic response of J-tube pull-in installation of the main platform for the umbilical cable under different wave directions. Finally, some instructive notices and mechanical properties during umbilical tie-back were put forward based on related modeling results. The hydrodynamic analytical result shows that the speed of the winch and the change of wave directions have very important effects on the process of umbilical cable pull-in through J-tube; the position where umbilical cable bends badly is where the von mises stress changes obviously as well, but the stress is still less than that permitted by API 2RD, and it can satisfy the request by the engineering safety.

Key words:umbilical cable; OrcaFlex; hydrodynamic analysis; different wave directions

Doi:10.3969/j.issn.1001-909X.2016.01.009

中图分类号:TV131.2；U674.38

文献标识码:A

文章编号:1001-909X(2016)01-0067-09

作者简介:张大朋(1987-)，男，山东临清市人，助理研究员，主要从事船舶与海洋工程结构物动态响应方面的研究。*通讯作者：朱克强(1956-)，男，教授，主要从事船舶与海洋工程结构动态响应方面的研究。E-mail: zhukeqiang@nbu.edu.cn

基金项目:长江学者和创新团队发展计划项目资助 (IRT0734); 国家自然科学基金项目资助(11272160); 国家高科技发展计划(“863”计划)项目资助(2014AA09A224)

收稿日期:2015-05-25修回日期:2015-06-08

张大朋，朱克强，牛天鑫，等.不同浪向下脐带缆与主平台回接过程中的动力学响应[J].海洋学研究,2016,34(1):67-75,doi:10.3969/j.issn.1001-909X.2016.01.009.

ZHANG Da-peng, ZHU Ke-qiang, NIU Tian-xin，et al. Dynamic response in the process of umbilical cable pull-in main platform through J-tube under different wave directions[J]. Journal of Marine Sciences, 2016,34(1):67-75, doi:10.3969/j.issn.1001-909X.2016.01.009.

E-mail: 1214265737@qq.com