复阻抗法验证凸极同步电机双反应理论研究
2016-04-23谢宝昌
谢宝昌
(上海交通大学 电子信息与电气工程学院, 上海 200240)
复阻抗法验证凸极同步电机双反应理论研究
谢宝昌
(上海交通大学 电子信息与电气工程学院, 上海 200240)
摘要::本文从同步电机电感和电枢反应磁势出发,推导单相交流供电在转子静止且无励磁时纯直轴、纯交轴,以及一般电枢反应状态下的电压方程和复阻抗,确定验证双反应理论的复阻抗关系,从而通过实验测量验证双反应理论的有效性。该方法也可以作为同步电机电感参数测量方法,有助于深入理解双反应理论和同步电机运行规律。
关键词:磁势; 电感; 双反应理论; 复阻抗
0引言
“电机学”是电气工程与自动化专业的重要基础课程,凸极同步电机是其重要内容,分析该类电机的核心是双反应理论。但“电机学”讲授时仅仅阐述该理论,没有通过实验来验证该理论,学生在学习过程中难以深入的理解[1-4]。
本文主要根据转子静止且无励磁状态下,凸极同步电机定子采用不同连接方式施加单相交变电压,在电机中形成直轴和交轴电枢反应脉振磁场,通过实验测量电枢电流和外施电压,计算输入复阻抗,并通过比较复阻抗来验证双反应理论的有效性。
1双反应理论
凸极同步电机由于转子气隙不均匀,使得气隙磁导在交轴和直轴不同,电枢磁势在空间产生的磁场与磁势波形不同。为了分析电枢磁势产生的磁场,Blondel提出了双反应理论,即将电枢磁势分解为直轴和交轴磁势两个分量,然后分别确定这两个分量产生的磁场,再将两个磁场合成为电枢磁场,从而得到电枢感应电势。由于双反应理论采用叠加原理,因此磁路必须是线性的。

图1 电枢磁势及其直轴和交轴分量
图1给出了电枢磁势基波(粗实线)及其直轴和交轴分量(细实线)波形和时空矢量分解。图2给出了直轴和交轴磁势分量产生的气隙磁场(实线)及其基波磁场(虚线)波形。
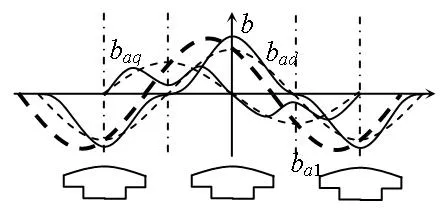
图2 电枢磁场直轴和交轴分量及其基波
不考虑转子励磁,图3给出了利用双反应理论产生电枢绕组磁链的过程。

图3 电枢磁势、磁场和磁链关系
2同步电机电感
三相对称运行时,同步电机任意一相的电压方程为
us=Rsis+dψs/dt
(1)
其中,us为外加相电压,is为电流,ψs为磁链,Rs为电阻。
由图3得到不考虑转子励磁时的一相磁链ψs包括电枢漏磁链ψσ和电枢反应磁链ψa:
ψs=ψσ+ψa
(2)
漏磁链由一相绕组自漏磁链和其它两相绕组对该相绕组的互漏磁链组成,前者与自漏电感和自身电流有关,后者则与互漏电感和它相绕组电流相关,由于三相对称绕组的互漏电感相同,因此一相绕组的漏电感Lσ等于自漏电感Lsσ与两相绕组互漏电感Lmσ之差
Lσ=Lsσ-Lmσ
(3)
三相对称绕组对称电流幅值Im产生的基波磁势幅值Fa称为电枢反应磁势幅值[5]。
Fσ=1.5K1Im
(4)
其中K1为一相绕组单位电流产生的基波磁势幅值。
当电枢反应磁势幅值位于直轴或交轴时,可以得到相应的直轴或交轴电枢反应电感
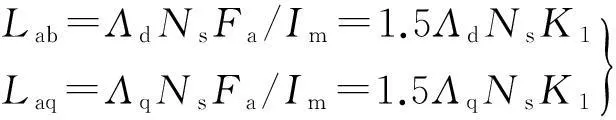
(5)
其中直轴和交轴磁路每极磁导分别为Λd和Λq,每相绕组有效串联匝数为Ns。
直轴(交轴)同步电感等于直轴(交轴)电枢反应电感与漏电感之和
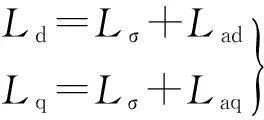
(6)
电枢反应磁链与直轴和交轴电枢反应磁势有关,设直轴超前定子相绕组电角为θ,则该相电枢反应磁链为
ψa=ΛdNsFadcosθ-ΛqNsFaqsinθ
(7)
3实验原理
忽略磁滞与涡流效应,电枢电流产生的磁场不会使静止转子励磁绕组损坏,更不会使电机饱和,保证磁路是线性的,这样就可以采用叠加原理,满足双反应理论应用的基本条件。
3.1直轴电枢反应实验原理
转子绕组开路,电枢绕组(星形连接)将B相和C相短接,再与A相构成串联电路,两端施加单相交流电压,测量A相电流和两端输入电压u1,如图4所示。
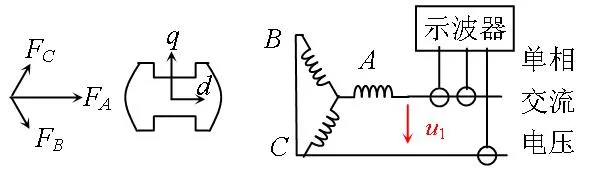
图4 直轴电枢反应实验示意图
由图4可知,uB=uC,u1=uA-uB,iA=-(iB+iC),转子直轴将与A相绕组轴线重合。由对称性得iB=iC=-iA/2。于是,电枢反应合成磁势必定位于直轴方向
Fad=1.5FA=1.5K1iA
(8)
电枢反应磁场只有直轴分量,根据式(3)、(5)、(6)、(7)和(8)可以得到三相绕组的磁链
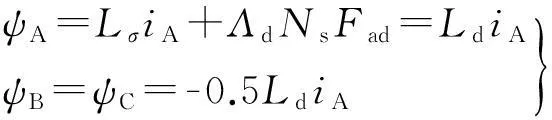
(9)
输入电流i1=iA,由式(1)和(9)得输入电压u1:
u1=1.5(Rsi1+Lddi1/dt)
(10)
式(10)用相量形式表示的正弦稳态电压方程为
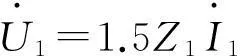
(11)
其中直轴同步电抗为Xd,复阻抗Z1=Rs+jXd。
3.2交轴电枢反应实验原理
直轴电枢反应实验结束后,锁定转子使直轴保持与A相绕组轴线重合,A相开路,B相和C相两端施加单相交流电压,测量输入电流和电压,如图5所示。
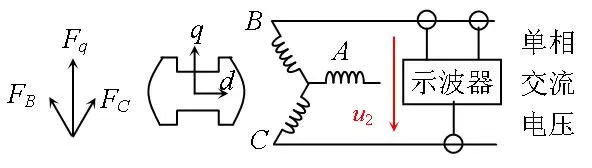
图5 交轴电枢反应实验示意图
由图5可知,u2=uB-uC,iA=0,iB=-iC,电枢磁势位于交轴,电枢反应是纯交轴性质,电枢合成磁势
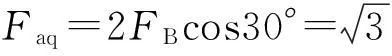
(12)
电枢反应磁场只有交轴分量,B相和C相磁链由式(3)、(5)、(6)、(7)和(12)得到
ψB=-ψC=LqiB
(13)
输入电流i2=iB,由式(1)和(13)得电压u2
u2=2(Rsi2+Lqdi2/dt)
(14)
式(14)用相量表示的正弦稳态电压方程
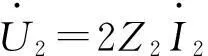
(15)
其中交轴同步电抗为Xq,复阻抗Z2=Rs+jXq。
3.3一般电枢反应实验原理
转子仍然锁定,B相开路,A相与C相两端施加单相交流电压,测量输入电流和电压,如图6所示。
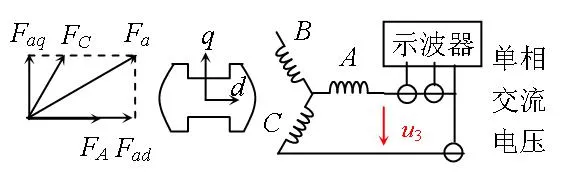
图6 直轴电枢反应实验示意图
图中u3=uA-uC,iB=0,iA=-iC,电枢磁势同时存在直轴和交轴分量,不妨设直轴与A相轴重合
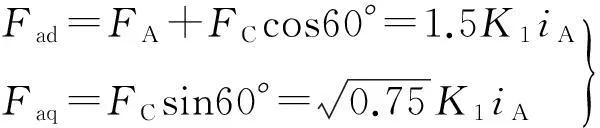
(16)
电枢反应磁势分别在A相和C相绕组的磁链

(17)
输入电流i3=iA,由式(1)和(17)得电压u3:

(18)
当直轴超前A相轴线θ=60°电角时,式(18)变为
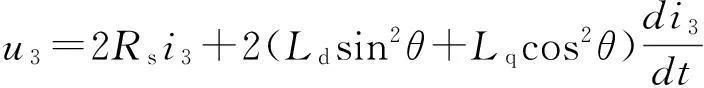
(19)
式(19)用相量表示的正弦稳态电压方程
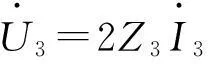
(20)
其中复阻抗Z3=Rs+jXdsin2θ+jXqcos2θ=Z1sin2θ+Z2cosθ。
4实验结果与分析
本实验在我校BMEL-IIA电机系统实验平台上进行,同步电机型号为TF(D)21/10.5-4,为了使励磁绕组感应电压不超过允许值,实验过程监测励磁绕组感应电压不超过110 V,功率表读数保留两位有效数字,实验测得每相绕组电阻为3.69 Ω。
先按图4施加直流电压使得转子直轴与A相轴线对齐,再改为施加交流电压,测量输入电压Ua、电流Ia、功率Pa和励磁绕组感应电压Uf,结果如表1所示。
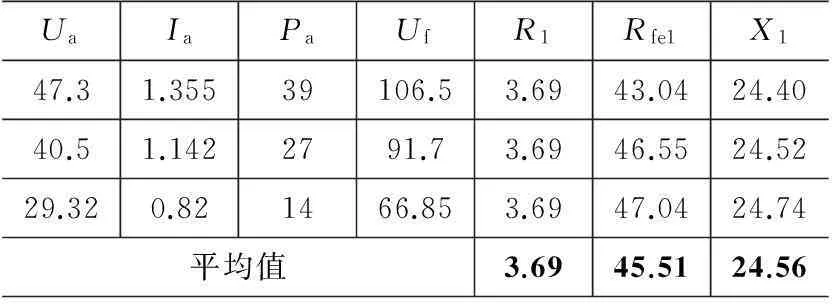
表1 直轴电枢反应实验结果
由于时变磁场在定转子中产生磁滞与涡流损耗,因此采用图7所示的统一形式的等效电路
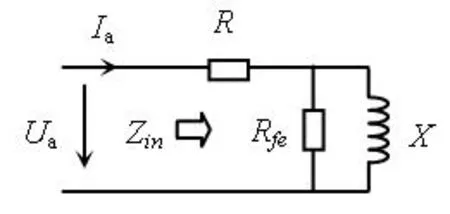
图7 等效电路
由等效电路得到输入复阻抗
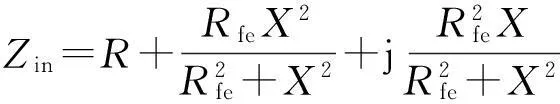
(21)
由图4和表1计算Zin,图7中的电阻R=1.5Rs=1.5R1,Rfe=1.5Rfe1,X=1.5X1=1.5Xd。不考虑铁耗时的输入复阻抗Zin=R+jX=1.5Z1。
由式(11)计算复阻抗Z1=Zin/1.5,结果如表1所示,不考虑铁耗时的复阻抗Z1=R1+jX1=3.69+j24.56 Ω。
转子锁定,由实验图5测量输入交流电压Ua、电流Ia、功率Pa和励磁绕组感应电压Uf,计算复阻抗Zin/2,结果如表2所示。励磁绕组存在很小的感应电压是因为直轴与A相绕组轴线没有完全对齐。
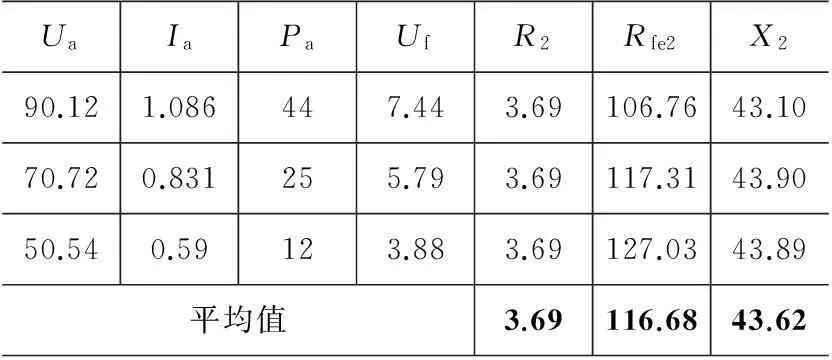
表2 交轴电枢反应实验结果
由图5和表2计算输入复阻抗Zin,图7中的电阻R=2Rs=2R2,Rfe=2Rfe2,X=2X2=2Xq。不考虑铁耗时的输入复阻抗Zin=R+jX=2Z2。
由式(15)计算复阻抗Z2=Zin/2结果如表2所示,不考虑铁耗时的复阻抗Z2=R2+jX2=3.69+ j43.62 Ω。
转子仍锁定,由实验图6测量输入交流电压Ua、电流Ia、功率Pa和励磁绕组感应电压Uf,图7中的电阻R=2Rs=2R3,Rfe=2Rfe3,X=2X3。不考虑铁耗时的输入复阻抗Zin=R+jX=2Z3。
由式(21)计算Zin/2,结果如表3所示,不考虑铁耗,复阻抗Z3=R3+jX3=3.69+j26.89 Ω。
最后按照式(22)计算复阻抗相对误差
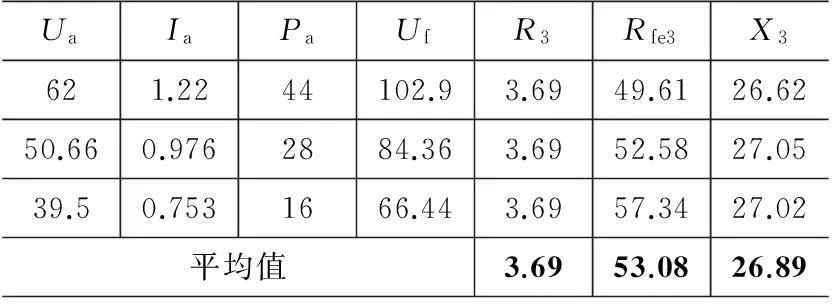
表3 一般电枢反应(θ=60°)实验结果
(22)
理论上磁路线性且没有铁耗时的相对误差应该为零,但考虑到测量因素和系统本身磁滞与涡流等非理想状态,会存在一定误差。将θ=60°和复阻抗计算结果Z1、Z2和Z3代入式(22)得到相对误差δz=8.97%。
5结语
本文通过对单相交流供电凸极同步电机在转子静止且无励磁状态下,就纯直轴、纯交轴和一般状态这三种情况下电枢反应实验得到的脉振磁势进行电磁分析,揭示了三种实验电路内在复阻抗的关系,获得验证双反应理论的复阻抗比较法,该方法也可作为同步电机电枢电感参数测量方法,这些内容将有助于深入理解凸极同步电机电感参数和运行规律。
参考文献:
[1]许实章,电机学[M],北京:机械工业出版社,1982年
[2]周顺荣,电机学[M],北京:科学出版社,2007年
[3]孙旭东,王善铭,电机学[M],北京:清华大学出版社,2006
[4]汤蕴璆,电机学[M],北京:机械工业出版社,2014年
[5]谢宝昌,交流电机绕组的气隙磁势与电势计算[J],南京:电气电子教学学报,第36卷,第2期,2014
Research on Complex Impedances to Verify Double Reaction Theory of Salient Synchronous Machines
XIE Bao-chang
(SchoolofElectronicInformationandElectricalEngineering,ShanghaiJiaoTongUniversity,Shanghai200240,China)
Abstract:Based on inductance parameters and magneto-motive forces of synchronous machines, voltage equation and its complex impedance forms are derived for the pure d-, q-axis and general armature reactions under single-phase power supply and stationary rotor without field current. Complex impedance relationship is determined to validate the double reaction theory. Complex impedance tests can verify its effectiveness and can also be used to get inductance parameters of salient synchronous machines, which will help us to deeply understand the theory and operations of salient synchronous machines.
Keywords:agneto-motive force; inductance; double reaction theory; complex impedance
文献标识码:A
文章编号:1008-0686(2016)01-0060-04
作者简介:谢宝昌(1965-),男,博士,副教授,主要从事电机与电器的教学与研究工作,E-mail:bcxie@sjtu.edu.cn
收稿日期:2014-09-01;修回日期:2015-10-12
中途分类号:TM31
