铁路混凝土工程钢筋机械连接螺纹接触应力分析

陈　强，谷　牧，钟志强，徐先俊(.蒙西华中铁路股份有限公司，北京　0007;.中国铁道科学研究院铁道建筑研究所，北京　0008;.安徽金星预应力工程技术有限公司，安徽合肥　5)



铁路混凝土工程钢筋机械连接螺纹接触应力分析

陈强1，谷牧2，钟志强3，徐先俊3
(1.蒙西华中铁路股份有限公司，北京100073;2.中国铁道科学研究院铁道建筑研究所，北京100081;3.安徽金星预应力工程技术有限公司，安徽合肥231135)

摘要:选取3种典型直径(φ16，φ25，φ32)的钢筋，每种钢筋选取3种螺距，开展了钢筋直螺纹连接组件接触有限元分析，系统地研究了直螺纹连接接头组件的变形、螺牙尖角应力及接触应力分布特征。结果表明:在设计连接接头长度下，采用不同的螺距时，连接接头组件的静力受力性能均满足钢筋连接的强度及变形要求，但考虑到受力的均匀性、钢筋几何尺寸特点、加工难易程度及可行性，建议φ16，φ25，φ32钢筋机械连接采用的螺距分别为2.0，2.5，3.0 mm;拉伸荷载作用下，螺牙接触对均在一侧密贴，另一侧分离，螺牙接触面分离量在首尾螺牙处最大;除首尾螺牙的尖角应力较大外，其余螺牙的应力迅速降低并较为均匀，即螺牙数目越多(螺距越小)，螺牙承受荷载的均匀程度越好，但加工越困难;连接组件的螺牙尖角应力与钢筋直径、螺距大小有关;螺牙接触对的接触点最大应力在螺牙的尖角处，而向螺纹中径则迅速衰减并稳定，即螺纹连接组件的牙体荷载传递区域主要在中径附近。

关键词:机械连接接触应力螺距有限元分析

现浇混凝土施工中，绑扎法是粗钢筋连接最为常见的方法之一，也是国内外最早采用的传统方法。该法具有施工简便、对工人的技术熟练程度要求低、不受气候影响等优点，但同时存在浪费钢材、钢筋偏心连接会产生附加剪应力等缺点。为解决上述问题，美国、日本、德国在20世纪70年代中期，研制出机械连接技术，如冷挤压连接、锥螺纹连接、直螺纹连接等技术，并制定了相应的国家标准，广泛应用在公路桥梁、地铁、核电站、大跨度抗震结构中。对粗钢筋而言，机械连接技术已经取代了传统的焊接绑扎工艺，在公路桥梁、水坝等大型重点建筑工程中得到了广泛应用［1-2］。刘永颐等［3］在钢筋机械连接技术规程编制方面所做的大量工作引领了中国机械连接方式的潮流。中国建科院结构所［4］测试了套筒挤压接头的抗疲劳性能与套筒挤压道次的关系，为套筒挤压接头应用到动载结构作出了一定的铺垫。邢怀念等［5］开展了直螺纹套筒连接性能试验研究。对于锥螺纹连接技术，江苏省建科院给出了一系列的螺纹牙距推荐值，并取得了良好的实际效益［6］。在众多国内外学者试验、研究成果的基础上，国内相关部门组织编写了相应的规范(或规定)，作为钢筋机械连接技术应用的指导性标准［7-9］，极大地促进了其应用。

已有的研究文献大多以试验性的探索为主，侧重于连接接头工艺改进［10-11］，缺乏系统的理论及试验研究。近年来，由于铁路工程的快速修建，对大量应用的粗钢筋均须采用机械连接技术以保证钢筋连接的有效性和经济性。原铁道部组织编写了《铁路混凝土工程钢筋机械连接技术暂行规定》［12］，并通过设立科研课题开始系统地研究铁路混凝土工程用钢筋机械连接技术。本文基于“等强度连接”原则，采用常用的3种直径的钢筋，选定不同的螺距，对设计出的连接接头开展了理论研究，验证连接接头设计的准确性，进一步优化合理的螺距规格，以促进钢筋机械连接技术在铁路混凝土工程中的应用。

1　钢筋直螺纹连接接触应力分析有限元模型

钢筋直螺纹连接是通过直螺纹连接接头和钢筋丝头螺纹旋合在一起来实现连接的，属于典型的接触问题。这种接触使整个接头构件表现出一种与状态相关的高度非线性行为，计算过程中需要较大的计算资源。接触问题分析存在2个难点:①在求解问题之前，接触区域是未知的，表面之间是接触还是分开随载荷、材料、边界条件和其它因素而变化;②大多的接触问题需要计算摩擦力，而摩擦力的非线性特性会使整个问题求解的收敛变得非常困难。直螺纹连接接头钢筋丝头螺纹与套筒的接触面是一个空间螺旋曲面，其模型的建立十分复杂。由于螺纹的升角一般在2°30'左右，建模时可以忽略升角的影响。考虑到钢筋本体、连接接头和连接组件都是轴对称的，而且拉压过程中外加荷载也是对称于其中心轴线的，假定套筒和钢筋滚丝头是标准的圆形，没有椭圆度，因此力学分析模型可以作为轴对称问题来处理。利用MIDAS-FEA中的静接触分析功能，主要采用平面四边形单元、平面三角形单元模拟钢筋及连接接头本体，采用线接触单元模拟螺牙之间的接触，连接接头及钢筋的材料本构模型均采用Von-Mises模型(屈服准则)。详细的接触理论可参阅MIDAS理论有关手册。需要说明的是，本次接触有限元分析的目的是优选螺牙牙距及定性分析连接接头的力学特性，主要关注钢筋丝头螺牙、连接接头螺牙的受力分布，承担荷载的比例，连接接头组件的力学特性，接触压力及组件的变形特性。模型中不考虑螺纹预紧力，而对屈服后的连接接头组件的受力及变形特性亦不作深入研究。钢筋直径及螺纹规格见表1。

表1　钢筋直径及螺纹规格

1.1连接接头接触力学分析模型尺寸

由于接触分析的重点是螺牙，而三角形螺牙的螺距最大仅为3.5 mm，因此模型尺寸以钢筋直径为基准，连接接头壁厚取实际值，连接接头以外的钢筋长度统一取80 mm。有限元模型尺寸见图1。

图1　有限元模型尺寸

1.2有限元模型说明

对于同一种直径的钢筋连接接头有限元模型而言，其几何尺寸完全相同，而螺牙的数量、螺牙网格尺寸、接触面的数量及钢筋网格数量不同。为了便于提取计算结果，模型划分时，将螺牙(三角形区域)映射网格均分为8等分，这意味着牙距不同时，网格尺寸略有不同。钢筋上的螺牙与连接接头上的螺牙接触面均定义为接触对。

模型材料主要有HRB335和45#优质碳素钢2种。HRB335材料特性参数:弹性模量为2.0×1011N/m2，泊松比为0.2，质量密度为7.8×103kg/m3，材料本构模型取Von-Mises模型，屈服强度fskb=335 MPa。45#优质碳素钢的材料特性参数:弹性模量为2.1×1011N/m2，泊松比为0.26，质量密度为7.89×103kg/m3，屈服强度取值fsks= 355 MPa;接触的截面非线性定义为刚性接触(滑移但不允许穿透);接触组的刚度比例因子取1.0，静态摩擦系数取0.15。

根据求解问题的特点，有限元计算边界条件及加载方式见图2，即钢筋一端固定，钢筋中心线竖向(Y向)约束。考虑接触滑移计算求解收敛性，假定套筒边界竖向约束。荷载取钢筋0.9fskb时对应的荷载，根据套筒受力净面积换算成面荷载，进而转化成线荷载。根据计算结果，3种连接组件的线荷载集度均约为217 N/mm。

典型的有限元模型网格划分见图3。

图2　有限元计算边界条件及加载方式

图3　典型的有限元模型网格划分

2　直螺纹连接组件有限元计算结果及分析

2.1变形计算结果及分析

直螺纹连接组件变形计算结果见表2。可见，在0.9倍钢筋屈服应力的荷载作用下，φ16的钢筋连接接头长度范围内的X向(拉伸)变形为0.009 8～0.010 5 mm，平均应变约为(245～263)×10－6;φ25的X向变形为0.011 3～0.018 5 mm，平均应变约为(188～308)×10－6;φ32的X向变形为0.012 4～0.020 2 mm，平均应变约为(165～269)×10－6。总体来说随着钢筋直径的增加，连接接头的长度增加，长度范围内的变形也相应增加。钢筋直径相同的条件下，由于连接接头的长度相同，长度范围内的拉伸变形相差不大，与螺距大小的关系并不明显。分析螺牙接触面的分离距离可知，接头范围内的首、尾螺牙接触面的分离距离最大，而中间部分螺牙的分离距离较为均匀，且数值较首、尾螺牙迅速衰减，表明首、尾螺牙的受力最大。这与连接接头试验过程中的断裂现象基本吻合(试件断裂位置为第1个螺纹处)。

表2　直螺纹连接组件变形计算结果

图4为3种直径钢筋部分螺距时连接组件X向变形等值线云图。

图5为3种直径钢筋部分螺距时螺牙接触面分离距离变化曲线。

图4　3种直径钢筋部分螺距时连接组件X向变形等值线云图

图5　3种直径钢筋部分螺距时螺牙接触面分离距离变化曲线

2.2机械连接组件应力计算结果及分析

直螺纹连接组件最大应力计算结果见表3，试验荷载作用下连接组件应力等值线云图见图6。可见，在0.9倍钢筋屈服应力的荷载作用下，螺牙尖角的应力分布很不均匀，由于受应力集中的影响，首、尾螺牙尖角处的应力最大，且大部分应力值均超过了钢筋及连接接头材料的屈服应力，而中间螺牙的尖角应力则迅速降低，如φ16(P = 2.0 mm)，φ25(P = 2.5 mm)， φ32(P = 3.0 mm)的连接接头除首尾螺纹以外的平均应力分别约为195 MPa(套筒螺牙)、225 MPa(钢筋螺牙)，210 MPa(套筒螺牙)、200 MPa(钢筋螺牙)，120 MPa(套筒螺牙)、120 MPa(钢筋螺牙)。这说明首、尾螺纹的尖角处最先出现塑性变形，其他螺牙则近乎均匀地传递荷载。这种螺牙应力的分布状态较好地解释了连接组件静力及疲劳试验过程中断裂失效为何总发生在第1圈螺纹处，与试验破坏特征基本吻合。

表3　直螺纹连接组件最大应力计算结果

图6　试验荷载作用下连接组件应力等值线云图

2.3螺牙的接触应力分布特征分析

为了准确掌握螺牙的应力沿钢筋长度方向的分布特征以及螺牙接触点压力沿螺牙高度的变化特点，从有限元分析结果中提取了每一种钢筋的3种螺纹规格的尖角应力及接触点压力并绘制其变化曲线。仍以φ16(P = 2.0 mm)，φ25(P = 2.5 mm)，φ32(P = 3.0 mm)为例加以分析。

图7(a)为φ16，P = 2.0 mm时螺牙尖角Mises应力沿试件长度方向的变化曲线。可见，钢筋螺牙尖角Mises应力普遍高于套筒螺牙应力，首尾2个螺牙的接触点应力均较大，钢筋体和连接接头上的螺牙尖角应力分布均从两边向中间衰减，总体上较1.5 mm螺距的螺牙应力略微平缓，尾螺牙尖角处Mises应力小于套筒螺牙尖角应力。图7(b)为φ16，P = 2.0 mm时螺牙接触点应力沿钢筋长度方向的分布曲线，除首尾2个螺牙的接触点应力变化较为明显外，其他的螺牙接触点应力分布均较均匀。

图7　φ15，P = 2.0 mm时螺牙应力沿钢筋长度方向分布曲线

图8为φ25，P = 2.5 mm时螺牙应力沿钢筋长度方向分布曲线。可见螺牙尖角Mises应力及接触点应力仍然具有首尾螺牙应力较大、中间螺牙应力较小的特点，首螺牙钢筋体螺牙尖角应力高于连接接头螺牙尖角应力，而尾螺牙处连接接头螺牙尖角应力大于钢筋体螺牙尖角应力，螺牙平均应力约230 MPa;同一高度螺牙接触点应力变化则较为平缓，首尾螺牙的接触点应力稍大于中间螺牙接触点应力，尾螺牙的应力普遍高于首螺牙应力。

图9为φ32 mm，P = 3.0 mm时螺牙应力沿钢筋长度方向分布曲线。可见钢筋体首螺牙尖角应力最大，约303.74 MPa，而后迅速减小并基本保持在约110 MPa。套筒首螺牙的应力较小，约为85 MPa，并逐渐增大，至尾螺牙处尖角应力约为155.57 MPa。首螺牙处钢筋应力大于连接接头应力，尾螺牙处连接接头应力高于钢筋体应力。而对于同一高度而言，首螺牙的接触点应力较大，而后迅速减小，其余螺牙的接触点应力基本上较为均匀，螺牙的荷载传递效果良好。

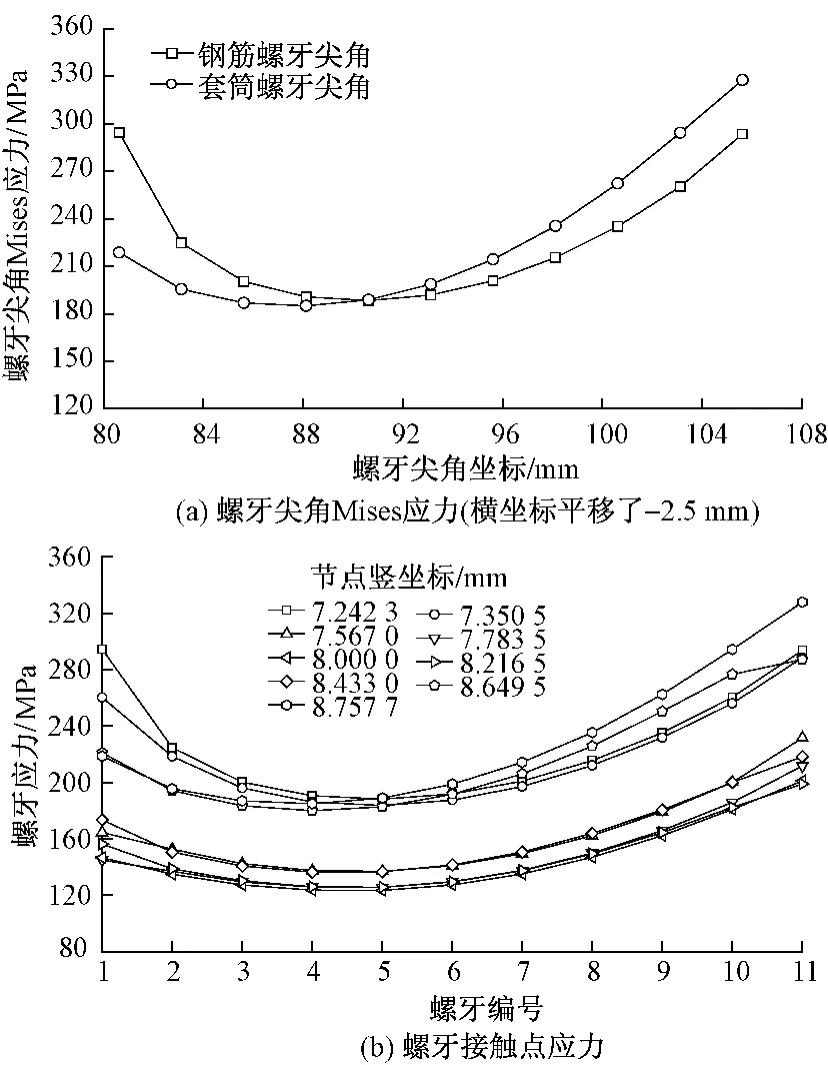
图8　φ25，P = 2.5 mm时螺牙应力沿钢筋长度方向分布曲线

图9　φ32，P = 3.0 mm时螺牙应力沿钢筋长度方向分布曲线

图10为φ16(P = 2.0 mm)，φ25(P = 2.5 mm)，φ32(P = 3.0 mm)3种连接接头螺牙接触点应力沿高度方向的分布曲线。可知，除首尾两个螺牙的接触点应力变化较为明显外，其他的螺牙接触点应力分布较为均匀，但总体上仍然有从尖角向螺牙中径变小的趋势，中径70%螺牙高度范围内应力相对较为均匀，表明中径范围螺牙承担主要的荷载传递功能，螺牙承担荷载的效果良好。

图10　3种连接接头螺牙接触点应力沿高度方向分布曲线

3　主要结论

通过φ16(P = 1.5，2.0，2.5 mm)，φ25(P = 2.5，3.0，3.5 mm)，φ32(P = 2.5，3.0，3.5 mm)连接接头组件的接触有限元分析，系统地研究了直螺纹连接接头组件的变形、螺牙尖角Mises应力及接触点应力分布特征。主要结论如下:

1)不论采用何种螺距，所设计的连接接头组件的静力受力性能均能满足钢筋连接的强度及变形要求，但从受力的均匀性、钢筋几何尺寸特点、加工难易程度及可行性而言，建议φ16，φ25，φ32钢筋机械连接采用的螺距分别为2.0，2.5，3.0 mm。

2)拉伸荷载作用下，螺牙接触对均在一侧密贴，另一侧产生分离;螺牙接触面分离距离均在首尾螺牙处最大。

3)除了首尾螺牙的尖角Mises应力较大外，其他螺牙的应力水平迅速降低，螺牙数目越多(即螺距越小)，螺牙承受荷载的均匀程度越好，但加工越困难;不同直径、不同螺距连接组件的螺牙尖角Mises应力水平不同。

4)螺牙接触对的接触点最大应力在螺牙高度的尖角处，向螺纹中径范围内迅速衰减并稳定，螺纹连接组件的牙体荷载传递区域主要在中径附近。

参考文献

［1］王治群.钢筋直螺纹连接技术在桥梁工程中的应用［J］.湖南交通科技，2005，31(3):59-62.

［2］龚万江，刘维娟.用于土木工程中的钢筋机械连接技术［J］.交通科技，2005(3):107-108.

［3］刘永颐，徐有邻.钢筋等强直螺纹连接［J］.施工技术，1998(6):30-31.

［4］中国建筑科学研究院结构所.带肋钢筋套筒连接挤压接头性能研究［J］.施工技术，1994(6):6-8.

［5］邢怀念，张小鹏，刘增利，等.钢筋滚轧直螺纹套筒连接性能试验研究［J］.工业建筑，2009，39(增):846-849.

［6］陶咏，刘晓章.钢筋锥螺纹连接接头螺纹牙距研究［J］.建筑机械化，1999(1):33-34.

［7］中华人民共和国住房和城乡建设部.JGJ 107—2010钢筋机械连接技术规程［S］.北京:建筑工业出版社，2010.

［8］中华人民共和国建设部.JGJ 108—1996带肋钢筋套筒挤压连接技术规程［S］.北京:建筑工业出版社，1996.

［9］中华人民共和国建设部.JGJ 109—1996钢筋锥螺纹接头技术规程［S］.北京:建筑工业出版社，1996.

［10］吴弘，孙广垠.浅析钢筋连接的发展及其在施工中的质量控制［J］.科技情报开发与经济，2007，17(4):262-263.

［11］郑文俊，潘江波，宁英杰，等.钢筋机械连接质量问题原因分析及处理措施［J］.交通标准化，2009(10):174-176.

［12］中华人民共和国铁道部.铁建设［2010］41号铁路混凝土工程钢筋机械连接技术暂行规定［S］.北京:中华人民共和国铁道部，2010.

(责任审编李付军)

Analysis of Thread Contact Stress in Rebar Mechanical Connection in Railway Concrete Engineering

CHEN Qiang1，GU Mu2，ZHONG Zhiqiang3，XU Xianjun3

(1.Mengxi－Huazhong Railway Co.，Ltd.，Beijing 100073，China;2.Railway Engineering Research Institute，China Academy of Railway Sciences，Beijing 100081，China;3.Anhui Jinxing Prestressed Engineering Technology Co.，Ltd.，Hefei Anhui 231135，China)

Abstract:T he contact FEM analysis was carried out with three types of rebar diameter(φ16，φ25，φ32)and three types of thread pitch for each rebar diameter，and deformation，stress of screw tooth cusp and contact stress distribution were researched in detail.Results show that with designed mechanical connection length and different thread pitch，static performance of all the rebar mechanical connection assembles meets the deformation and strength requirements of code.T he proposed thread pitches of rebar with diameters of φ16，φ25 and φ32 are 2.0，2.5，3.0 mm based on comprehensive consideration of stress uniformity，geometry dimension of rebar，process difficulty and feasibility.W ith the stretching load，contact pairs are closed at one side and separated at other side.T he maximum amount of separation existed at the first thread and last thread.Stresses of middle threads decreased rapidly and tend to uniformity except larger stresses of the first and last thread sharp angle.Uniformity of thread load transference become better with more threads(smaller thread pitch)，but process becomes more difficult.Stress level of thread sharp angle is related to rebar diameter and thread pitch.T he maximum contact stress is located at thread sharp angle，decreases rapidly to the direction of thread mean diameter and tend to uniformity，it means that the load transferring part of thread is mainly mean diameter range.

Key words:M echanical connection;Contact stress;T hread pitch;FEM(Finite Element M ethod)

作者简介:陈强(1972—)，男，教授级高工，工学博士。

基金项目:南广铁路公司科技研究开发计划(南广合201107号)

收稿日期:2015-12-22;修回日期:2016-01-29

文章编号:1003-1995(2016)03-0150-07

中图分类号:TU511.3

文献标识码:A

DOI:10.3969/j.issn.1003-1995.2016.03.36