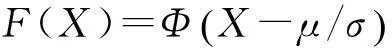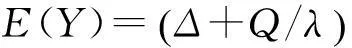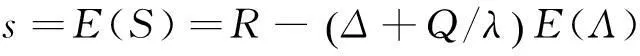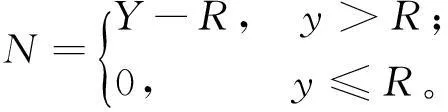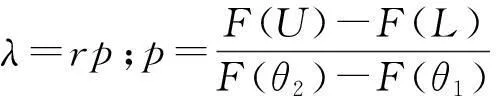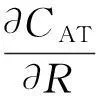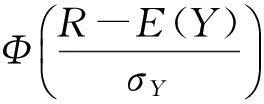随机库存模型中最优过程均值选择研究

吴燕燕,　袁建明

(合肥工业大学 管理学院,安徽 合肥　230009)



随机库存模型中最优过程均值选择研究

吴燕燕,袁建明

(合肥工业大学 管理学院,安徽 合肥230009)

摘要:通常过程均值的选择和生产-库存控制的决策是分开确定的,但是过程均值的确定会影响不合格品出现的概率,从而影响生产-库存的决策。文章讨论了在需求是随机的且质量特征服从截尾正态分布的情况下最优过程均值和生产-库存模型相应决策变量联合确定的问题。在该模型中, 允许缺货发生且缺货量完全延期供给,同时给出了模型的凸性证明和应用实例。通过灵敏度分析,研究了各参数及截尾方式对过程均值和生产-库存决策的影响。

关键词:截尾正态分布;过程均值;需求不确定;库存控制

在生产过程中,过程均值的选择在很多领域被广泛关注。最优过程均值的确定非常重要,因为它直接影响到过程的零缺陷率、材料耗费成本、报废或返修成本以及产品质量特性偏离顾客目标值产生的质量损失等。而在库存控制中则要研究何时订货或组织生产以及订购多少货物或生产多少产品,以使得库存系统的总支出最少或总利润最大。通常过程均值的选择和生产-库存控制的决策是分开确定的,但是过程均值的确定会影响不合格品出现的概率,从而影响生产-库存的决策。为了减少整条供应链中的总成本,特别是为了控制生产和库存的总成本,过程均值和生产-库存决策应该同时决定。

国内外研究者对此开展了卓有成效的研究。文献[1]讨论了过程受控但不满足规格限时过程均值的优化设计问题;文献[2]在质量特征分别服从正态分布、对数分布和指数分布的情况下,讨论了单边规格限时的最优过程均值的确定问题;文献[3]考虑了在截尾正态分布的情况下最优过程均值的确定问题;文献[4]研究了时变需求下变质性物品的随机生产库存问题;文献[5]考虑了多个产品生产过程中的最优过程均值确定问题;文献[6]建立了一个同时确定最优过程均值、规格限制和生产质量的模型；文献[7]考虑了生产多种产品时同时确定最优过程均值和生产控制限的问题;文献[8]考虑了质量特征服从正态分布时,随机库存模型最优过程均值的选择问题。在很多有关过程均值问题的文献中,都假定总体分布是正态的,然而在有些情况下质量输出不可能取负值,也不可能为无穷大,而是在某个范围内取值[3]。例如,食品包装的净含量、钢材锻件的长度等。本文在假定需求是随机的且质量特征服从截尾正态分布的情况下,讨论了最优过程均值的确定和生产-库存决策,并研究了过程参数、截尾方式及成本参数对最优过程均值和生产-库存决策的影响。

1模型的假定与记号

本文的主要假定和参数如下:

(1) 假设质量特征变量X服从截尾正态分布,即X～N(μ,σ2),且X∈[θ1,θ2],其中μ为过程均值,σ为单位产品所需原材料的标准差。

(2) 不合格产品或报废产品没有残值。

(3) 需求是随机的,Q为总订货量,Λ为每单位时间需求的随机变量,σΛ为单位时间需求的标准差,E(Λ)为平均需求率,且E(Λ)<∞,从而单位时间期望的订货次数为E(Λ)/Q。

(4) 缺货允许发生且短缺量全部延期供给。

(6) 装配费为A,原材料固定订货成本为Ar,单位时间单位产品的库存费为h,单位时间单位原材料的库存费为hr,单位产品的缺货损失费为π,固定生产成本为b(b>0),增值因子为α(α>0),每单位原材料成本为c,Φ为标准正态分布累积分布函数,L(μ)为标准损失函数。

(7)R为产品在再订货点时的库存量,S为安全库存随机变量,s为期望安全库存,s=E(S),N为缺货次数随机变量,n为期望缺货次数n=E(N),CAT为单位时间的期望平均费用。

2数学模型

设F(x)和f(x)分别是均值为μ、方差为σ2的正态分布的分布函数和概率密度函数,即

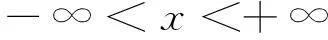
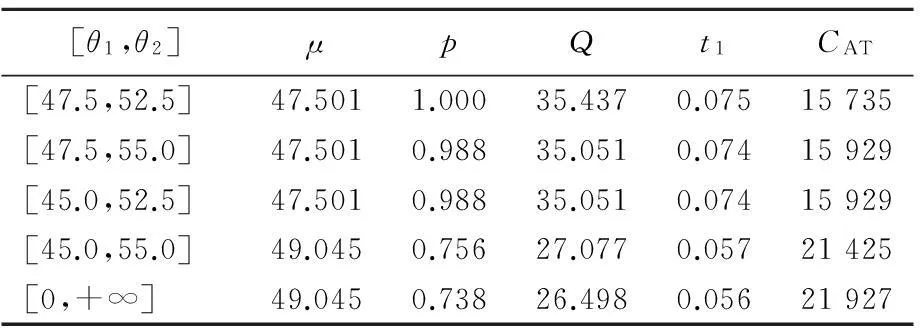
(1)

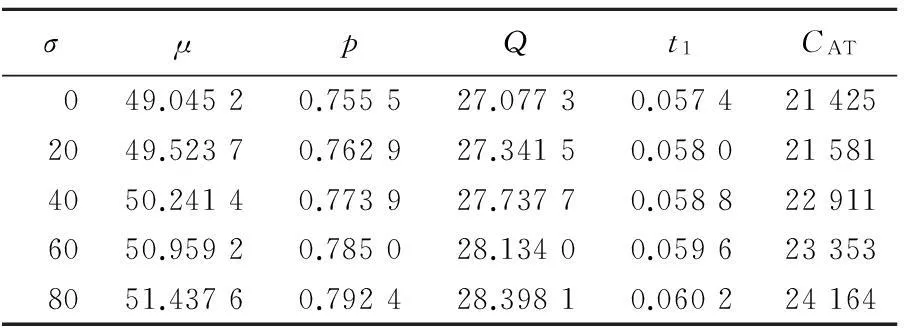
由于假定质量特征变量X服从均值为μ和方差为σ2的正态分布,其中μ是不随时间变化而变化的,即过程均值不会随时间漂移，且X不会小于某个值θ1,同时也不会大于某个值θ2,同时产品合格时需要满足一定的范围,即当L≤X≤U时产品是合格品,其中θ1

(2)

概率密度函数为:

(3)

于是,产品的合格概率为:

(4)

图1　合格产品和原材料的库存水平变化示意图

在推导模型的总成本时,采用了经典的周期模型,下面由图1给出与模型相关联的几项费用。

(1) 装配成本。由于单位时间的组装次数为E(Λ)/Q,从而单位时间的装配费为:

(5)

(2) 库存保管费。图1a描述了合格产品库存随时间变化而变化的过程。在一个周期[0,T]内,库存从S+Q开始到S结束,其中S为安全库存。由于期望需求率是一个常数,从而现有的期望库存的变化是线性地从S+Q变到S,其均值为S+Q/2,从而单位时间的期望库存费为h(s+Q/2),其中s为期望安全库存。同时在库存建立期[T-τ,T],库存水平的增加率为λ,直到有Q个合格品生产出来用于满足需求。在库存建立期每单位时间期望库存费为h[E(Λ)τ]/2=[hQE(Λ)]/2λ。从而单位时间总的期望库存成本为:

(6)

(7)

将(7)式代入(6)式得:

(8)

(3) 短缺量引起的缺货费。缺货费只有当前置时间需求量大于再订货点的量时才会发生,设缺货的量为N,则N满足以下关系式:

从而每周期的期望缺货量n(R)为:

(9)

其中,L(μ)为标准正态损失函数,其表达式为:

其中,Φ为标准正态分布累积分布函数;φ为标准正态分布的概率密度函数。

从而单位时间的期望缺货费用为:

(10)

(4) 原材料控制成本。原材料控制成本包括原材料订购成本和原材料库存成本。当生产商向供应商订购原材料时要支付一个固定的订购费Ar,而当原材料用于生产时,它以rμ的速度减少,从而在t(t≤τ)时,原材料的库存为:

(11)

将τ=Q/λ代入(11)式,得到每周期原材料的库存成本为:

从而每周期单位时间原材料总控制成本为:

(12)

(5) 直接生产成本。假设产品的直接生产成本为原材料成本的一个线性函数[8-9],其表达式为:h(X)=b+αcX,其中α≥1。从而每周期生产Q个合格产品所需的期望总成本为:

同时每周期生产Q个合格产品的期望原材料成本为:

从而每周期单位时间总的期望生产成本为:

(13)

从而可得库存系统中单位时间期望平均费用为:

(14)

3理论结果及求解方法

现在的问题是寻求Q、R和μ的最优值,使得系统每单位时间期望平均费用CAT达到最小。为此,下面给出系统每单位时间期望平均费用CAT的相关性质。

定理1对于一切的Q>0,λ≥E(Λ),CAT为Q的下凸函数。

证明对于任意的Q>0,λ≥E(Λ),由(14)式两边对Q求偏导可得:

(15)

再由(15)式可得:

从而CAT是Q的下凸函数。证毕。

由定理1可知,令∂CAT/∂Q=0可得Q的最优值为:

(16)

与定理1类似的方法,易证以下定理2。

定理2对于一切的Q>0,λ≥E(Λ),CAT是R的下凸函数。

(17)

由上述的分析可知,在模型的求解过程中可先令Q0为经济订购批量，则有：

(18)

将(18)式代入(17)式求得R0,然后将Q0、R0代入(14)式求出过程均值μ0的最优值,再利用μ0求出相应的p和λ,将其代入(16)式求出Q1的值,将所求得的Q1代入(17)式中求出R1值,以此类推,直到所求得的2个连续CAT(Q,R,μ)值的误差小于给定的精度δ为止。具体的求解步骤如下。

(1) 令i=1,CAT0→∞,且有：

(3) 通过(14)式计算CAT的最小值求得相应的μi。

(4) 令CATi=CAT。

(5) 如果CATi

(6) 如果|CATi-CATi-1|>δ,则令i=i+1,转步骤(7),否则转步骤(8)。

(7) 通过(16)式求出Qi,转步骤(2)。

(8) 停止。

需要指出的是在步骤(3)中可以使用任何一种一维搜索算法来求出相应的最优过程均值,例如二分法、斐波那契法和0.618法等，本文采用的是0.618法。而μ的搜索范围为[L,L+zσ],其中z为一个预定的实数,而L为最低质量限制。值得注意的是,当μ=L时生产过程的产品合格率仅为50%,因而在现实的生产库存系统中,应尽量避免这种情况的发生,来减少产品的零缺陷率、材料耗费成本、报废或返修成本,提高企业的盈利能力。

4数值例子

设某工厂生产钢材,钢材长度X是一个连续性随机变量,服从截尾正态分布。其上下质量限制U、L分别为52.5 m和47.5 m;钢材长度不短于45 m(即θ1=45),但又不长于55 m(即θ2=55),钢材生产时的标准差σ=2 m,平均需求率E(Λ)=300根/a,单位时间需求的标准差σΛ=0根/a,生产率r=500根/a,装配费A=50千元,原材料订货成本Ar=20千元,产品的年库存费h=4 千元/根,原材料年库存费hr=1 千元/根,产品年缺货费π=7 千元/根，固定生产成本b=1千元/根,增值因子α=1,原材料成本c=0.5千元/m,固定前置组件时间Δ=0。通过Matlab 7.10软件和0.618法进行计算可得当正态分布截尾与不截尾时的生产-库存模型相应的决策变量,见表1所列。

由表1可知,如果质量输出分布的截尾性被忽略时,虽然最优过程均值的值是相同的,但是产品的合格率将会被低估,产品每次的生产批量和库存周期均减少,同时导致生产-库存系统的单位时间期望平均费用增加。

表1　正态分布截尾与不截尾时生产-库存模型相应的决策变量

5灵敏度分析

由于产品生产时所用原材料的量不一定都是关于目标值对称波动的,从而导致截尾的方式不一样;同时过程参数σ、σΛ和成本参数c、h、A也将会对生产-库存的决策产生影响[10]。在上例的基础上,单位产品所需原材料的标准差、单位时间需求的标准差、成本参数及截尾方式对生产-库存决策模型的影响见表2～表5所列。

由表2可知,随着单位产品所需原材料的标准差的增大,最优过程均值也随之增大,产品的合格率、生产批量逐渐减小,但却导致每周期单位时间期望的平均费用逐渐增加。因而厂商在生产过程中应尽量降低单位产品所需原材料的标准差,来减少产品生产过程中所造成的不必要的原材料浪费,从而降低生产成本,提高盈利能力。

表2　原材料的标准差σ的影响

由表3可知，当单位时间需求的标准差增大时,最优过程均值、产品的合格率和生产批量及每周期单位时间期望平均费用均逐渐增大。

表3　单位时间需求的标准差σΛ的影响

由于成本参数c、h、A只会对生产-库存模型中的决策变量产生影响,故当成本参数发生变化时,并不会对产品的最优过程均值这一生产参数产生影响。下面只考虑成本参数对每周期单位时间期望的平均费用的影响,并对其进行灵敏度分析。由表4可知,生产-库存决策系统每周期单位时间的期望平均费用均会随着成本参数c、h、A的增加而增加。

表4　成本参数c、h、A的影响

由表5可知,随着截尾方式上下限的逐渐放大,最优过程均值也随之增大,产品的合格率和产品的生产批量逐渐减小,但每周期单位时间的期望平均费用却逐渐增加。

表5　正态分布截尾方式的影响

6结束语

过程均值的选择是质量工程学中一个重要的命题,它对于生产效率的提高、产品质量的改进等具有重要的影响。传统的过程均值选择都是在质量特征服从正态分布这一假定下进行讨论的,但是这个假定有时并不成立。本文在假定需求是随机的且质量特征服从截尾正态分布的情况下,同时确定了最优过程均值和生产-库存模型相应的决策变量,并且对所建立的模型给出了凸性证明和数值例子及其相应参数的灵敏度分析。灵敏度分析表明:过程参数和截尾方式对每周期单位时间期望的平均费用的影响比成本参数对每周期单位时间期望的平均费用的影响更为显著,所以在生产-库存控制决策中应首先减小过程参数的变化范围和截尾方式的上下限。该模型为实际生产中对最优过程均值的选择及生产-库存控制决策提供了理论依据。

[参考文献]

[1]Wen D,Mergen A E.Running a process with poor capability[J].Quality Engineering,1999,11(4):505-509.

[2]Chen C H,Chou C Y.Determining the optimum process mean of a one-sided specification limit[J].International Journal of Advanced Manufacturing Technology,2002,20(6):439-441.

[3]张斌,王海燕,韩之俊.基于截尾正态分布的最优过程均值的确定[J].数理统计与管理,2008,27(1):106-110.

[4]鹿泉育,杨志林.时变需求下变质性物品的随机生产库存模型[J].合肥工业大学学报: 自然科学版,2011,34(6):935-940.

[5]Lee M K,Kwon H M,Hong S H,et al.Determination of the optimum target value for a production process with multiple products[J].International Journal of Production Economics,2007,107 (1):173-178.

[6]Chen C H,Khoo M B C.Optimum process mean and manufacturing quantity settings for serial production system under the quality loss and rectifying inspection plan[J].Computers and Industrial Engineering,2009,57(3):1080-1088.

[7]Park T,Kwon H M,Hong S H,et al.The optimum common process mean and screening limits for a production process with multiple products[J].Computers and Industrial Engineering,2011,60(1):158-163.

[8]Darwish M A,Abdulmalek F,Alkhedher M.Optimal selection of process mean for a stochastic inventory model[J].European Journal of Operational Research,2013,226(3):l481-490.

[9]Gong L,Roan J,Tang K.Process mean determination with quantity discounts in raw material cost[J].Decision Sciences,1988,29(1):271-302.

[10]Al-Fawzan M A,Hariga M.An integrated inventory-targeting problem with time dependent process mean[J].Production Planning and Control,2002,13(1):11-16.

Research on optimal selection of process mean in stochastic inventory model

WU Yan-yan,YUAN Jian-ming

(School of Management, Hefei University of Technology, Hefei 230009, China)

Abstract:It is very common that the process mean selection and production-inventory decisions are determined separately. However, the probability of nonconforming production will be affected by the choice of process means. Thus, the process mean influences other important production and inventory decisions. This paper jointly determines the optimal process mean and the other decision variables in the production-inventory model when the demand is a random variable and the quality characteristic obeys the truncated normal distribution. In this model shortages are allowed to occur and backlogged completely. In addition, the convexity of the model is proved and its application example is also shown. The influences of the parameters and the type of truncation on the determination of process mean and production-inventory decisions are examined by conducting a sensitivity analysis.

Key words:truncated normal distribution; process mean; demand uncertainty; inventory control

中图分类号:O213.1

文献标识码：A

文章编号：1003-5060(2016)03-0415-06

doi:10.3969/j.issn.1003-5060.2016.03.024

作者简介：吴燕燕(1989-),女,浙江湖州人,合肥工业大学硕士生;袁建明(1956-),男,江苏江阴人,合肥工业大学副教授,硕士生导师.

基金项目：国家自然科学基金重点资助项目(71131002)

收稿日期：2015-01-14；修回日期：2015-03-20