基于电能的桥箔爆炸FIRESET模型修正

邱林俊，胡云钦，李 东，魏贤华，代 波，任 勇

（西南科技大学 四川省非金属复合与功能材料重点实验室-省部共建国家重点实验室培育基地，四川 绵阳，621000）



基于电能的桥箔爆炸FIRESET模型修正

邱林俊，胡云钦，李 东，魏贤华，代 波，任 勇

（西南科技大学 四川省非金属复合与功能材料重点实验室-省部共建国家重点实验室培育基地，四川 绵阳，621000）

摘 要：针对FIRESET电爆炸模型认为爆炸过程中导体动态电阻是比作用量的函数，在应用于分析桥箔电爆炸放电回路与研究爆炸箔电爆炸特性时，存在计算误差大、不能直观反映电爆炸过程的缺点，采用电能取代比作用量，引入初始电阻率修正项，从而对FIRESET桥箔电爆炸的非线性动态电阻模型进行修正；利用修正模型对Al、Cu、Ni/Al多层膜3种爆炸箔的电爆炸曲线进行计算，结果几乎与测试结果完全重合，有效地改进了FIRESET模型的模拟偏差。表明利用电能修正FIRESET模型可以直观地反映电爆炸过程中由于温升和相变导致爆炸箔电阻变化的一般规律，有效地仿真电爆炸过程。

关键词：爆炸箔；FIRESET模型；爆炸曲线；动态电阻

当金属箔通过强脉冲大电流时，由于热效应迅速地发生从固态、液态到气态的相态转变，当继续加热时金属气体会发生电离，形成高温高压等离子体，等离子体向周围介质膨胀过程中会产生冲击波和光辐射，即电爆炸[1]。由于电爆炸过程中产生的等离子体具有高温高压特性，使得在武器安全点火、起爆系统等方面具有重要的应用前景。大量的学者对电爆炸进行了实验和理论方面的研究，其中对于金属箔电爆炸方面的理论研究，早在1975年，Sandia实验室的Tucker等人[2]就利用比作用量（g）来描述电爆炸中桥箔的非线性动态电阻（R），给出了电爆炸过程中桥箔电阻、电流及电压的计算方法。后来，美国LawrenceLivermore实验室的R.S.Lee[3-4]在比作用量理论基础上，建立了FIRESET模型来描述桥箔爆炸过程的电阻变化。虽然FIRESET模型的计算简便，能基本反映电阻的变化趋势，但是由于FIRESET模型未考虑桥箔的初始电阻，忽略了桥箔电爆炸过程中的体积变化，不能很好地反映电爆炸过程，导致模拟的偏差较大。大多数学者对FIRESET模型的修正，都是基于对ρ——g关系的重组，但没有考虑初始电阻，在模拟结果上提升的空间不大，依然存在一定的误差。成剑[5]等提出以焦耳热作为爆炸过程的主线，建立了放电电阻的理论计算模型，也探索了桥箔电阻随吸收能量变化的理论关系。杨家志[6]等采用PSpice[7]软件建立金属丝电阻变化模型，认为金属箔的电阻的增量与其沉积的能量成正比，能够很好地解释由于焦耳热造成桥箔温升导致的电阻变化，但不能解释经过相变及以后的电阻变化规律。鉴于以上原因，本论文基于FIRESET模型简洁、便于计算的优点，用电能代替比作用量，对FIRESET模型做合理修正，并比较修正前后模型在动态电阻模拟的结果。

1　金属桥箔电爆炸回路分析

1.1爆炸回路及测试

在电爆炸测试过程中，由于焦耳热的作用，导致金属物理状态在短时间内发生一系列的相变，由此伴随着电阻的急剧变化。所以，在电爆炸中桥箔电阻是一个和桥箔沉积电能有关的动态电阻，如图1所示。

图1　电爆炸过程吸收电能-相变-电阻关系Fig.1 Evolution of phase and resistance of exploding foil absorbing electrical energy

桥箔电爆炸发火回路是由等效电阻R1、等效电感L、发火电容C及桥箔动态电阻组成的振荡放电回路，简称放电回路。其中，R1为145 mΩ，L为0.44 μH，C为0.2 μF。所制备的Al、Cu和Ni/Al多层膜3种爆炸箔的厚度均为4μm，桥区尺寸均为400μm ×400μm，其初始电阻R0分别为32mΩ、17mΩ和42 mΩ。

本文采用罗果夫斯基线圈电流探头检测电流波形，用高压探头检测桥箔两端电压波形。测量时将罗果夫斯基线圈套在待测电流回路的导线上，通过线圈感应出小电流，从而间接测量脉冲电流，再根据电流转化关系，得到流过桥箔的爆炸电流。桥箔两端动态电压测量是把高压探头两端直接与桥箔两端电极相连。电流及电压输出信号由数字示波器记录。图2是桥箔电爆炸装置及电流电压测量系统示意图。

图 2 电爆炸测试机理简图Fig.2 Schematic diagram of measurement of electrical explosion

在电爆炸的放电回路中，金属桥箔电爆炸过程的等效电路方程为基尔霍夫回路方程，见式（1）：

式（1）中：R(t)即为动态电阻；t为时间；I为电流；U0为充电电压，3种爆炸箔的U0均为2 000 V。电爆炸模拟的最终结果是得到电流和电压与时间的爆炸曲线，其核心是求解基尔霍夫方程，实质是解决动态电阻问题，因此电爆炸模拟实际就是对电爆炸过程中的动态电阻的模拟。

1.2FIRESET模型

FIRESET模型的主要特点是在忽略了导体爆炸时尺寸变化效应前提下，根据实验数据统计，认为导体电爆炸过程中其电阻率ρ为电流作用积分g(t)的函数，如式（2）所示：

其中：

电流作用积分又称比作用量，通常指单位截面积的电流通过1Ω电阻所沉积的能量[8]。在FIRESET模型中，假定桥箔电阻率峰值发生在某一固定时刻tb，爆炸时刻对应的比作用量为g0。经过大量实验统计，g0具有如下规律：

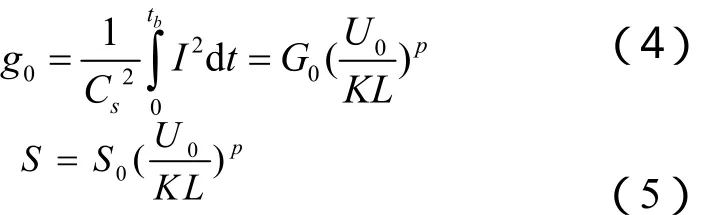
式（4）～（5）中：Cs是桥箔的横截面积。根据式（2），可以得到初始时刻t0、爆炸时刻tb及爆炸后（＞＞tb）的电阻率ρ0、ρtb、ρ∞。

由此，FIRESET模型主要用了4个特征参量来描述导体电阻变化率，分别是A、B、S、g0，这些参量与材料本身有关，可以通过大量实验统计获得。其中导体爆炸后的电阻率A，爆炸时电阻率峰值0.35A+ B，爆炸时电阻率的峰值幅值宽度S，导体爆炸时刻的比作用量g0，大多数材料的FIRESET模型参量特征值已得到广泛研究[9]。在实验中，对Al、Cu、Ni/Al多层膜3种爆炸箔的FIRESET参数进行了统计，统计结果如表1所示。

表1　FIRESET模型的参数Tab.1 Parameters of FIRESET model

图3　电阻与比作用量关系曲线Fig.3 The relationship of the resistivity and the specific action

采用FIRESET模型对Cu箔爆炸过程中的ρ——g曲线进行拟合，并与实验结果曲线比较，如图3所示。由图3可见，实际的ρ——g曲线与FIRESET的模拟结果有一定的偏差，这是由于FIRESET模型在物理意义上考虑有一定偏差，难以真实地反映电爆炸的物理过程。尤其FIRESET模型中的初始时刻存在明显缺陷，在初始时刻计算的ρ趋近于0，而实际情况爆炸箔总存在一个初始电阻R0。

2　FIRESET模型的修正

鉴于FIRESET模型的不足，本文在前人对桥箔沉积能量与桥箔电阻关系的研究基础上，根据电爆炸受焦耳热有关的热力学原理，考虑到爆炸箔由于能量沉积使其温升和相变导致电阻变化的物理事实，建立由焦耳热引起桥箔电阻率变化的ρ——E函数来描述动态电阻率的变化情况。用电能E替换FIRESET模型中的比作用量g，仍将保留FIRESET模型简单、易于计算的优势。此外，尤其针对FIRESET初始电阻率偏差的问题，对模型添加常数项ρ0。假设电能全部沉积在桥区上，则单位质量桥箔材料沉积的电能E（本文所论述的电能都是指单位质量沉积能量）如式（9）：

式（9）中：W为电流对桥箔做的功；ω为桥箔的质量密度；d为桥箔长度；Cs为桥箔的横截面积。由此定义桥箔电阻率随沉积能量的变化方程，如式（10）：

根据式（10），可以得到修正模型中初始时刻t0、爆炸时刻tb及爆炸后（＞＞tb）的电阻率ρ0、、ρ∞：

综上所述，FIRESET模型基于电能修正后需要5个特征参量来描述导体电阻率变化，分别是A、B、S、e0、ρ0，这些参量与材料本身有关，可以通过大量实验统计获得。其中导体爆炸稳定后的等效电阻率A+ρ0，爆炸时电阻率峰值A/3+B+ρ0，初始电阻率ρ0，爆炸时电阻率的峰值幅值宽度S，导体爆炸时刻沉积电能E0，根据实验测试统计，可以基本确定A、B、S、e0、ρ0的值。在实验中，对Al、Cu、Ni/Al多层膜3种爆炸箔的FIRESET参数进行了统计，统计结果如表2所示。

表2　FIRESET修正模型的参数Tab.2 Parameters of modified FIRESET model

根据新建立的修正模型，对两种模型的参数进行对比，FIRESET模型主要考虑的是电阻率和比作用量的关系，其参数主要由爆炸时刻电阻率ρtb和爆炸后稳定的等效电阻率ρ∞来确定，如表1所示。而FIRESET修正后的模型主要考虑的是电阻率和桥箔本身沉积能量的关系，其参数主要由初始电阻率ρ0、爆炸时刻电阻率ρtb、爆炸后的电阻率ρ∞共同决定。相对传统FIRESET模型，修正模型考虑了初始电阻率的存在，在设计上针对实际爆炸情况更加合理，可解决FIRESET模型初始时刻模拟误差大的缺点。

修正后的FIRESET模型模拟桥箔电阻率随桥箔沉积能量的变化曲线如图4所示。

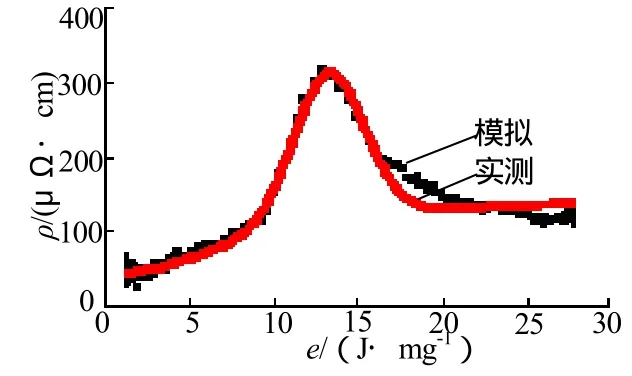
图4　电阻率与电能密度关系曲线Fig.4 The relationship of the resistivity and energy density

由图4可见，爆炸箔的电阻率随着桥箔沉积能量的增多而不断上升，当爆炸箔被加热到汽化阶段时，其电阻率达到最大值，此时通过爆炸箔的电能继续增加，已经达到汽化状态的金属气就会发生击穿，变成电阻率极低的等离子体，等效电阻率便会急剧下降。而后，桥区发生断裂，但在高频振荡电流的作用下，仍存在一个趋于常值的等效电阻，整个爆炸过程中电阻率呈现了合理的变化趋势。在爆炸前，模拟曲线几乎和实际曲线重合，这是由于模型的修正不仅考虑了电爆炸过程中由于温升和相变引起的爆炸箔电阻近似变化，而且考虑了初始电阻，有效地解决了FIRESET初始时刻误差大的问题。然而，修正模型相对于电爆炸的实际情况，在爆炸后仍然有一定的偏差，这是由于桥箔爆炸过程中忽略了汽化和电离过程中的体积膨胀，爆炸后处于断路状态，其具有容抗的性质，而笔者的模拟是基于纯电阻模型，所以存在一定的偏差，但不影响对电爆炸过程的理解。修正后的模型能够很好地解释电爆炸过程中桥箔吸收能量，由于温升和相变导致的电阻变化，同时也避免了由于复杂相变引起的电阻率繁杂的计算过程。

3　爆炸箔动态电阻模拟

采用FIRESET修正模型中给出的桥箔动态变化规律来描述桥箔电阻R(t)。将动态电阻R(t)代入基尔霍夫回路方程（1）。并对此微分方程组采用四阶-五阶变步长龙格-库塔算法求解，可将微分方程分解，得到y1、y2、y3随时间t的变化规律，如式（16）：

当计算到E0时，所对应时刻就是桥箔爆发时刻，该时刻对应电流就为桥箔爆炸时电流。本文采用MATLAB语言编写上述微分方程组的计算程序，用该程序计算桥箔电爆炸过程的爆发电流及电压曲线。

图5～6是金属桥箔爆发时通过FIRESET模型及新模型计算的爆发电流、电压曲线和实验测量的爆发电流、电压曲线。

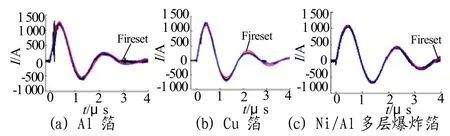
图5　爆发电流曲线的计算值和实验值的比较Fig.5 Comparison of burst current in calculation and experiment

图6　爆发电压曲线的计算值和实验值的比较Fig.6 Comparison of burst voltage in calculation and experiment

从图5中可以看出，经过修正后的FIRESET模型与实验结果符合得更好，相对原模型有一定的提升。从图6中可以看出，在初始时刻，FIRESET模型总是有一个很大的误差，这主要是FIRESET模型没有考虑初始电阻R0的存在，使其在初始时刻模拟的电压值趋于0，与实际偏差很大。通过修正后，爆发电压曲线在爆发前几乎和实验曲线完全重合，但是在爆发后仍然存在一些问题。这是由于桥箔爆炸后，处于断路状态，具有容抗性质，由于模拟是在整个过程中把桥箔等效为纯电阻模型，故存在一定误差，还需要进一步探索。总而言之，FIRESET模型修正后的计算曲线与实验曲线在电爆炸过程中几乎完全相吻合，相对于FIRESET模型有很大的提升。这是由于模型的修正是基于电爆炸过程的能量转换机理，根据实际爆炸过程对能量的吸收情况，由于温升和相变引起的爆炸箔的动态电阻变化曲线，相对传统FIRESET模型，更加接近物理事实。

4　结论

本论文根据FIRESET模型的优势与不足，引入初始电阻率ρ0，重组模型参数，利用电阻率——电能沉积关系描述了爆炸箔的动态电阻特性。模型修正后的ρ——E曲线相比FIRESET模型中ρ——g曲线与实验结果的符合度有了大幅提高。根据修正后的动态电阻模型，计算了Cu、Al和Ni/Al 3种爆炸箔回路放电特性，并与相应的实验测量结果进行对比，结果电流电压曲线几乎和实验结果完全吻合，相对于FIRESET模型也有显著提升。这是因为对修正模型是建立在温升和相变使爆炸箔电阻变化的规律上的，能合理解释电阻变化的一般规律，可为进一步研究电爆炸机理提供更多有价值的渠道。

参考文献：

[1]王莹.电爆炸导体及其应用[J].爆炸与冲击,1986,6(2):184-192.

[2]Tucker T J,Stanton P L.Electrical Gurney energy:A new concept in modeling of energy transfer from electrically exploded conductors[R].SAND-75 -0244,1975.

[3]Lee R S.Fireset[R].Lawrence Livermore National Lab.,CA (USA),1988.

[4]Lee R S,Osher J E,Chau H H,et al.1 MJ electric gun facility at LLNL[R].Lawrence Livermore National Lab.,CA (United States),1992.

[5]成剑,栗保明.电爆炸过程导体放电电阻的一种计算模型[J].南京理工大学学报,2003,27(4):371-375.

[6]杨家志,刘钟阳,牛秦洲,等.电爆炸过程中金属丝电阻变化规律的仿真分析[J].桂林理工大学学报,2010,30(2):300-304.

[7]Tuinenga P W.SPICE:a guide to circuit simulation and analysis using PSpice[M].Prentice Hall PTR,1995.

[8]杨集,杜涛,赵翔,等.基于电容放电单元的爆炸丝起爆特性数值分析[J].太赫兹科学与电子信息学报,2014,12(3):461-465.

[9]冯长根,伍俊英,陈郎,等.桥箔电爆炸过程数值计算分析[J].含能材料,2004(12):484-487.

Modification of FIRESET Model of Exploding Foil Based on Energy

QIU Lin-jun,HU Yun-qin,LI Dong,WEI Xian-hua,DAI Bo,REN Yong
(State Key Laboratory Cultivation Base for Nonmetal Composites and Functional Materials,Southwest University of Science and Technology,Mianyang，621000)

Abstract：FIRESET model of foil exploding considered dynamic resistance of explosion as a function of specific action,it has the disadvantages of significant error in the circuit analysis of the exploding foil and the investigation of electric explosion characteristics.In this paper,the FIRESET nonlinear dynamic model was modified through replacing specific action with energy and introducing initial resistance.The calculated burst curves by the modified model were in good agreement with the experimental curves for the exploding of Al,Cu and Ni/Al.It is more effective than the FIRESET model,because the modified model based on energy can directly reflect the exploding process associated with resistance change due to phase transition and temperature increasing.

Key words：Exploding foil；FIRESET model；Explosion curve；Dynamic resistance

基金项目：西南科技大学军工培育项目（批准号：13zxpt01）

作者简介：邱林俊（1990 -），男，硕士研究生，主要从事电爆炸研究。

收稿日期：2015-07-18

中图分类号：TJ450.1

文献标识码：A

文章编号：1003-1480（2016）01-0006-05