基于鲁棒不确定性的应急物资配送策略

朱佳翔,谭清美,蔡建飞,邓淑芬

(1.常州大学 商学院,江苏 常州 213164;2.南京航空航天大学 经济与管理学院,江苏 南京 210016)



基于鲁棒不确定性的应急物资配送策略

朱佳翔1,谭清美2,蔡建飞1,邓淑芬1

(1.常州大学 商学院,江苏 常州 213164;2.南京航空航天大学 经济与管理学院,江苏 南京 210016)

摘要：针对应急物资配送过程中救灾信息具有鲁棒不确定性特点，构建应急物资配送多阶段多目标鲁棒优化模型，并在此基础上给出鲁棒控制策略。鲁棒优化目标函数中设计运输成本最优、运输时间最少以及用户满意度最大等优化目标，充分考虑“鲁棒不确定性因素”对决策结果的影响，更适合完成突发事件下的应急救援物流任务，比静态环境下的一般规划模型更具有柔性。在鲁棒优化模型基础上给出鲁棒H∞策略，既能够抑制正态分布、均匀分布噪声等外部不确定输入扰动，同时又能够抑制成本参数、配送时滞等内部不确定性扰动，对于既定成本目标控制的平稳实现具有重要支撑作用。基于鲁棒优化的应急物资配送鲁棒控制策略，对于解决突发事件下的应急物资配送决策问题具有重要的应用价值与实际意义。

关键词：应急物流配送;鲁棒优化;多目标决策;鲁棒H8策略

一、引言

进入21世纪,突发事件频繁发生,应急物资配送优化与决策越来越受到关注[1-4]。就应急物流的早期研究来说,Kemball-Cook等人[5]首先提出应急物资配送时物流管理的重要性,通过加强物流管理可以提高应急物流系统中物资配送的效率。此外，国外一些学者基于应急供应链的视角,给出了几种应急供应链优化模型,但提出的模型假设都是以完备的信息掌握为前提[6-8]。

近年来,国内外学者在应急物资配送方面的研究,就研究问题而言,有学者研究了应急物流路径优化问题,如Sheu[9]建立混合模糊聚类算法模型用以解决应急物资的调度与配送;王绍仁等[10]研究了震后应急救援物资运输路线安排决策;陈森等研究了未定路网结构情况下应急物资车辆配送问题模型[11]。就不确定性研究方法而言,有模糊数学方法,如Teodorovic[12]研究了模糊顾客需求的应急物流车辆路径间题,并运用Gillett[13]提出的算法进行求解;郭子雪等[14]研究了带有模糊参数的应急物资筹集问题决策模型。有灰色决策方法,如周鹏霞等[15]研究了基于灰色层次法的城市应急能力评估系统;张英菊[16]研究了基于灰色多层次评价方法的应急预案实施效果评价模型。有随机规划方法,如Husein Onur Mete等[17]采用随机规划研究了应急救灾中药品配送的路径及定位问题; Barbarosoglu等[18]构建两阶段随机规划模型来描述应急资源调度问题。在应急物流领域的鲁棒优化方法,主要有Ali Bozorgi-Ami[19]、朱建明[20]、王晶[21]、张玲等[22]针对应急物流中的不确定性选址、配送等问题、研究了多目标鲁棒模型的最优性与均衡。国内外研究应急物流决策中的方法,大多仅局限于模糊及灰不确定性,鲁棒不确定性影响研究较少。

本文在研究应急物资配送的优化策略时,考虑了深层次的鲁棒不确定性策略问题。针对信息不完备环境下的应急物资配送系统,提出了基于鲁棒不确定性的应急配送运作模型,并设计了一个典型算例验证了该鲁棒运作模型的科学性,提出的鲁棒策略为突发事件下的供应链应急配送决策者提供有价值的参考。

二、问题描述

应急物资配送系统中,物流中转仓库被视为上下游之间的中介。应急物资配送系统作为一个整体,设共有T个计划期,整个供应链应急计划系统的动态规划过程是在[0,T]时间内完成。将[0,T]分成个n时段(tk-1,tk)k个配送物资品目和J个需求点。应急物资配送计划设计目的是为解决候选物流中转仓库L的选址问题,并可以检查应急物资配送系统的效率。

(一)假设条件

1.假设突发事件发生后的应急物资配送决策中,配送区域仅局限于没有遭受破坏的道路网络,而不考虑因道路损毁需用直升机进行救灾物资配送的受灾区域。

2.假设应急配送的物资仅限于一般救灾物资,而不考虑那些需保持冷藏或者要求其他特种运输设备配送的救灾物资。

3.假定突发事件下的应急物流配送过程中,可以掌握的可用性和可及性信息,如受灾物资需求数量、受灾人数等部分已知,部分缺失。

4.假设应急物资需求是一个离散时间常数,并在一个给定时间段内到达,即时间段可以用灰数来表示。

5.假定应急物资救援配送时,应急部门能够动员军用、民用车辆去协助救援配送,不考虑车辆数量约束的限制。

(二)变量解释

除应急物资配送的中转仓库候选点、配送物资品目(w)的权重以及用来表示候选位置是被选上作为配送中转仓库的二进制变量z等参数外,其余的变量和参数都与时间相关。应急物资配送模型的参数及具体变量的定义,总结如下。

三、应急物资配送计划

(一)应急配送目标

命题一:

1.在鲁棒不确定性条件下,应急物资配送虽然大多时间不考虑经济成本,但限于救灾资源的稀缺性,我们在应急配送的后期,仍然会考虑应急配送的成本问题,即实现最小化成本的目标。假设f1为应急物资配送的成本,则f1作为多优化目标之一的目标函数为

2.在鲁棒不确定性条件下,应急物资配送要考虑配送效率,即运输时间的最小化问题。令f2为应急物资配送的最少运输时间,则应急物资集货站、中转仓库、需求点之间的运输时间一旦确定,就可以计算出应急物资配送的总时间。其目标函数为

上游运输时间Til(t)可用如下表达式计算,公式为

而下游运输时间也同理可得。

3.在鲁棒不确定性条件下,应急物资配送要考虑需求方对应急配送的满意度问题。设f3表示应急物资配送的满意度。则其目标函数为

主要目的是使受灾区域获得应急物资的满意度极大化,并使得应急物资分配公平最大化。满意度的计算公式为

(二)应急配送约束

命题二:

1.应急物资配送的上述三个鲁棒优化目标函数确定后,着手解决约束问题。首先,考虑无效运输问题,此类问题如果不解决,就无法保证应急物资配送成本目标的实现。保证运输有效性的约束为

2.同理,推算出同一时刻进出救灾物资中转站的物资数量达到平衡,以避免中转站出现物资饱和或空转问题,其约束如等式

3.以此类推,装运任一品目的应急物资都不能超载,其约束不等式为

应急物资中转站选址约束为

在集货站装运已集齐的应急物资约束为

各种品目的应急物资被订购的约束为

此外,在应急物资配送规划中,假设受灾地区所需应急救灾物资因不可抗随机因素影响无法在该期交付,则可延迟至下一期配送,而不是放弃时间的有效性。则每一时刻t,在每个应急物资供应点i实际配送物资的供应能力,如式(1)所示。每个应急物资配送需求点j的实际需求量的计算公式如式(2)所示

(1)

(2)

(三)应急配送算法步骤

应急物资配送计划的目标、约束函数嵌入到鲁棒优化模型之中,构建基于鲁棒不确定性的应急物资配送多阶段决策,其算法步骤如下:

2.对于每个应急物流的随机状态ei∈E,实行第一步,于是Bn-1=(bn-11,bn-12,…,bn-1l)。

4.对每个应急物流的随机状态ei∈E,实行第三步,于是Bk-1=(bk-11,bk-12,…,bk-1l)。依次取k=n,n-1,…,2,1,重复计算第三步、第四步n次,即可得到每个时段对应的最优解。

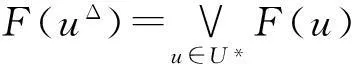
(四)鲁棒H∞控制策略

针对鲁棒最优目标实现问题,给出应急物资配送最优目标实现的鲁棒H∞控制算法定理。

定理1对于初始最优解:uΔ=(uΔ(t1),uΔ(t2),…,uΔ(tn)),在存在外部扰动情形下,无法确定是否达到预期优化目标。在不确定环境下应急物流配送系统,要保证在差情景下仍能维持应急物资配送系统的最优性能,其离散时滞系统的H∞状态反馈控制为

(3)

其中,x(k)∈Rn为鲁棒总目标最优化下的状态;u(k)∈Rm为最优化目标控制输入;w(k)∈Rl为最优目标扰动输入,为l2有限;每一构成不超过1;z(k)∈Rp为控制输出。假设所有状态是可测的。此处,正数时滞满足:0≤di<∞,i=1,2。作为时滞系统(3)的H∞控制器,u(k)=Kx(k)为状态反馈律。将时滞系统(3)应用于状态反馈律时,易推导出w(k)到z(k)的应急物流最优目标控制的闭环系统,如式(4)所示

(4)

其中,AK=A+B2K,CK=C+D12K。

引理1应急物资配送鲁棒总目标的实现,存在配送时滞、成本参数和外部输入需求满意度等不确定因素。如何在这些鲁棒不确定条件下,得到一个应急物资配送目标稳定控制,这就要求H∞控制设计的科学合理。对于给定的上述扰动的抑制程度γ>0,如果存在正定矩阵P,R1和R2使得式(5)在0≤di<∞,i=1,2条件下成立,则系统(3)是具有H∞范数界γ二次稳定的。其中,R1和R2为正定矩阵。

(5)

证明:给定Lyapunov函数如下:

(6)

由于式(6)暗含条件:

(7)

对上述Lyapunov函数进行微分,可得:

(8)

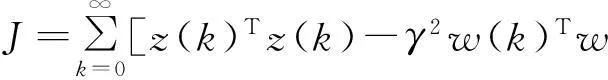
(9)

引理2应急供应链物资配送鲁棒最优成本计算后,需解决鲁棒最优目标的定位与控制问题。应急供应链运作成本的控制主要受到受灾区域救灾需求及配送时滞影响。给定dk为k时刻受灾区域救灾物资需求,τ为配送时滞参数, 0≤τ<∞,即在应急物资配送鲁棒目标的实现起到控制稳定作用。简化起见,令应急物资配送鲁棒总成本:

(10)

ΔC1,ΔC2,ΔC3为不确定性成本,u1,k为k时刻集货点到中转仓库的配送救灾物资量,为控制变量,u2,k为中转仓库至受灾点的救灾物资货物量,也是控制变量,则不确定环境下的应急物资配送需求的动态模型的矩阵形式为

(11)

四、数值分析

(一)典型算例

续表1

注:表中出现的负数表示短缺物资品目

表2　中转站与需求点之间应急物资配送鲁棒优化解

续表2

表1与表2反映了鲁棒不确定环境下,救灾物资供应点、中转站及需求点的四类救灾物资在满足成本、满意度双重最优情形下的最终鲁棒解。那么,上述计划期4个阶段的鲁棒最优解如下:

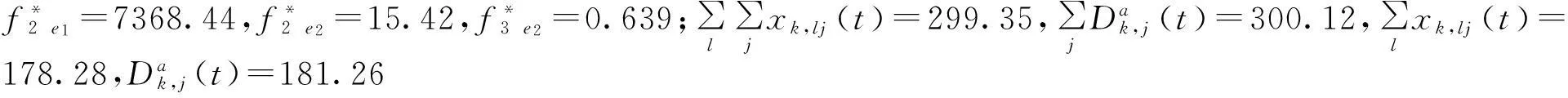
(二)鲁棒策略解

假设情形之一:外部不确定输入是正态分布噪声,dk～N(μ,σ2),μ=16,δ2=0.112;假设情形之二:外部不确定输入为均匀分布,dk～U(9,16);此外,不确定参数Δc1、Δc2、Δc3均服从均匀分布U[-0.25,0.25],包括时滞τ=1和τ=3两种情况。初始值x0=12,u1,k=8,u2,k=10,zk=6,仿真结果如图1、图2所示。

仿真计算结果表明,应急物资配送鲁棒化存在4个时段的最优决策。在第一个时段,应急物资配送的三个目标值分别是:配送总成本8328.75,最少运输时间为17.39,最大满意度为63.2%,说明突发事件的不可预测性给应急物资配送带来的不确定因素较多,以致三个目标值都不太理想;在第二时段,应急配送三个优化目标值分别是:配送总成本7368.44,最少运输时间为15.42,最大满意度为63.9%,较前一时段理想;在第三时段,应急配送的三个目标值分别是:配送总成本6667.28,最少运输时间为12.35,最大满意度为78.5%,也比前一时段理想;在第四时段,应急物资配送系统的三个优化目标值分别是:配送总成本4113.55,最少运输时间为9.65,最大满意度为97.88%,比前三个时段更为理想。这说明应急配送动态规划的四个时段中,总成本是逐渐下降的,运输时间是逐渐减少的,而配送满意度却在逐渐提高。因此,应急物资配送鲁棒优化模型与常规动态规划模型相比,更适合处理信息不完备条件下的应急物资配送阶段性决策问题,并考虑了鲁棒不确定性因素对决策结果的影响,比常规动态多目标规划更具有柔性。

进一步深度控制的仿真结果表明，在受灾区域需求满意度及配送时间目标基本满足前提下,随着时间k的推进,应急物资配送系统的成本目标的控制,由早期的波动较大变得平稳。图1与图2说明,应急物资配送系统的上游运输成本由最初的波动较大变得相对平稳。同时,应急物资配送总输出成本将在一个理想的条件下(γ=0.27)维持稳定。即根据鲁棒H∞控制策略下得到的最优控制uk能够抑制正态分布噪声、均匀分布形式外部不确定输入扰动；同时，抑制成本参数、配送时滞的不确定性扰动,使得整个应急物资配送系统的成本目标平稳实现。因此,求解应急物资配送最优目标鲁棒控制策略的过程,其实也是不断调整γ对策略进行调试的过程,当系统γ较小时,即对系统性能提出更高的要求,找到可行解的难度加大。但不可否认,鲁棒H∞控制策略仍然是解决应急物资配送最优目标实现的有效手段。

五、结论

本文考虑了“鲁棒不确定性”因素对应急物资配送策略的影响。首先,在鲁棒不确定性信息条件下提出了应急物资配送鲁棒优化模型,考虑了应急物资配送三个目标:最小总成本、最少运输时间及最大的满意度。这种应急物资配送多目标鲁棒优化模型与常规运筹学上的动态规划模型相比,考虑了随机性鲁棒因素对决策者决策结果的影响,尤其适用于处理信息不完备条件下的应急物资配送决策,比常规动态多目标规划更具有柔性。通过一个算例进行数值分析,结果表明，该模型能够经受检验,能解决突发事件中不完备信息下供应链配送决策问题,比较符合实际意义。其次，在鲁棒优化模型基础上进一步提出鲁棒H∞控制策略,通过仿真实验发现应急物资配送系统的上游运输成本由最初的波动较大变得相对平稳。同时,应急物资配送总输出成本将在一个理想的条件下维持稳定。鲁棒H∞控制策略能够抑制正态分布噪声、均匀分布形式外部不确定输入扰动,同时,抑制成本参数、配送时滞的不确定性扰动,使得整个应急物资配送系统的成本目标平稳实现。本文提出的基于鲁棒不确定性条件下的H∞控制策略,为我们在鲁棒环境下进行应急物资配送决策提供了有价值的参考,具有重要的实际意义。

参考文献:

[1] CAUCHEMEZ S. Estimating the Impact of School Closure on Influenza Transmission From Sentinel data[J]. Nature, 2008, 452: 750-754.

[2] FERGUSON N M. Strategies for Mitigating An Influenza Pandemic[J]. Nature, 2006, 442: 448-452.

[3] AHAY N. OR/MS Research in Disaster Operations Management[J]. European Journal of Operations Research, 2006,75: 475-93.

[4] LARSON R C, METZGER M D, CAHN M F. Responding to Emergencies: Lessons Learned and the Need for Analysis[J]. Interfaces, 2006, 36(6): 486-500.

[5] KIMBALL-COOK D,STEPHENSON I L Lesson in logistics from Somalia[J].Disaster,1984,(8):57-66.

[6] SULEIMAN T, WILLIAM ATE. The Emerging Area of Emergency Management and Engineering[C].IEEE Transactions on Engineering Management,1998.

[7] JINH-BING SHEU.Special Issue on Emergency Logistics Management Transportation Research Part E:Logistics and Transportation Review[J].Transportation Research Part E,2005,(41):459-460.

[8] TZENG G H, TANG T I, HUANG Y M,et al. Multi-objective Planning for A Production and Distribution Model of Supply Chain: Case of A Bicycle Manufacturer[J].Journal of Scientific & Industrial Research, 2006, 65 (4), 309-320.

[9] SHEU J B. An Emergency Logistics Distribution Approach for Quick Response to Urgent Relief Demand in Disasters[J]. Transportation Research Part E: Logistics and Transportation Review, 2005, 43(6): 687-709.

[10] 王绍仁,马祖军.震害紧急响应阶段应急物流系统中的LRP[J].系统工程理论与实践,2011,31(8):1497-1507.

[11] 陈森,姜江,陈英武,沈永平. 未定路网结构情况下应急物资车辆配送问题模型与应用[J].系统工程理论与实践,2011,31(5):907-913.

[12] TEODOROVIC D, RADIVO JEVIC G. A Fuzzy Logic Approach to Dynamic Dial-A-Ride Problem[J]. Fuzzy Set and Systems, 2000, 116(1): 23-33.

[13] GILLETT B L. Introduction to Recent Advances in Vehicle Routing Methods [M]. Amsterdam: North Holland Publishing, 1984.

[14] 郭子雪,齐美然. 带有模糊参数的应急物资筹集问题决策模型[J].计算机工程与应用,2011,47(23):217-219.

[15] 周鹏霞,党德鹏.基于灰色层次法的城市应急能力评估系统[J]. 计算机工程与设计,2012,(8):3023-3028.

[16] 张英菊. 基于灰色多层次评价方法的应急预案实施效果评价模型研究[J]. 计 算 机 应 用 研 究,2012,29(9):3312-3319.

[17] HUSEYIN ONUR M, ZELDA B Z. Stochastic Optimization of Medical Supply Location and Distribution in Disaster Ranagement[J]. Production Economics, 2013, 12(126): 76-84.

[18] BARBAROSOGLU G, Y A. A Two-Stage Stochastic Programming Framework for Transportation Planning in Disaster Response [J]. Journal of the Operational Research Society,2013, 34(55): 43-53.

[19] ALI BOZORGI-AMIRI M S J, S M J MIRZAPOUR. A Multi-Objective Robust Stochastic Programming Model for Dsaster Relief Logistics under Uncertainty[J]. OR Spectrum, 2011,(13): 1-29.

[20] 中国管理科学学术年会.管理科学学术会议论文集[C].北京:[出版者不详],2010.

[21] 王晶,张玲,黄钧.基于不确定需求的鲁棒应急物流系统[J].数学的实践与认识,2009,39(20): 53-60.

[22] 张玲,王晶,黄钧.不确定需求下应急资源配置的鲁棒优化方法[J].系统科学与数学,2010,30(10):1283-1292.

(责任编辑:张雅秋)

Emergency Supplies Distribution Strategy Based on Robust Uncertainty

ZHU Jia-xiang1，TAN Qing-mei2, CAI Jian-fei1, DENG Shu-Fen1

(1. Commercial college, Changzhou University, Changzhou Jiangsu 213164, China;2. School of Economics and Management, Nanjing University of Aeronautics & Astronautics, Nanjing Jiangsu 210016, China)

Abstract：In this paper, we build a multi-stage and multi-objective robust optimization model with a robust control strategy to cope with the robust uncertainty of relief information in emergency supplies distribution. The model is designed to achieve optimal transport costs, minimum transport time and optimization of user satisfaction with a full consideration of the impact of the robust uncertainty on decision-making. It is claimed that this model is more suitable for emergency rescue supplies and more flexible than regular models in the static environment. Robust H(∞) strategy given based on robust optimization model is capable of inhibiting both the external uncertain input disturbances such as normal noise and uniform noise, and the internal distribution such as cost parameters and time-delay, thus greatly facilitating the smooth realization of controlling the cost targets. It is argued that robust control strategy for emergency supplies distribution based on robust optimization is meaningful both theoretically and practically for solving problems in emergency supplies distribution.

Key words：emergency logistics distribution; robust optimization; multi-objective decision-making; Robust H(∞) strategy

中图分类号:F252.14

文献标识码：A

文章编号：1672-8106(2016)01-0106-11

作者简介:朱佳翔,男,常州大学商学院副教授。研究方向:物流供应链管理与决策方法。

基金项目:国家社会科学基金项目“智能生产与服务网络体系中军民融合产业创新平台及其供给战略”(15BGL029);江苏省高校哲学社会科学项目“协同理论视角下江苏省服务业集聚的空间适配性问题研究”(2014SJB470)。

收稿日期:2015-06-01

谭清美,男,南京航空航天大学经济与管理学院教授,博士生导师。研究方向:技术经济、物流供应链管理。