含中心微裂纹α-Fe拉伸与疲劳失效机理的原子模拟

袁玉全, 曾祥国, 胡燕飞

(1 四川理工学院 理学院, 四川 自贡 643000; 2 四川大学 建筑与环境学院, 四川 成都 610065)



含中心微裂纹α-Fe拉伸与疲劳失效机理的原子模拟

袁玉全1, 曾祥国2, 胡燕飞1

(1 四川理工学院 理学院, 四川 自贡 643000; 2 四川大学 建筑与环境学院, 四川 成都 610065)

摘要：采用分子动力学方法研究了含(010)[101]型中心裂纹的金属α-Fe在拉伸载荷和疲劳载荷作用下裂纹扩展的微观机制。研究表明，含有此类裂纹的体心立方金属铁在单轴拉伸载荷下，其破坏机制是一个以裂尖层错和孪晶变形共同存在、伴有裂纹钝化，并最终以孪晶变形为主的过程。疲劳失效是以孪晶形变为主，全位错、不全位错、层错共同作用的破坏机制，同时发现循环加载下 [11-1](-121)滑移系中孪晶形变比位错更容易发生，而且孪晶的出现，有利于减缓疲劳裂纹的扩展速度。含裂纹α-Fe变形与失效的过程，是一个位错、层错、孪晶和相变等多种微观机制共同作用的复杂过程。

关键词:分子动力学; 中心裂纹; α-Fe; 拉伸; 疲劳

PACS: 78.67.Bf

材料中不可避免地存在各种微缺陷如空位、孔洞、夹杂、微裂纹等，它们会严重影响材料的力学性能，材料的破坏往往从这些微缺陷附近开始萌生和扩展。因此，微缺陷附近的变形过程和失效机理吸引了工程界和学术界的广泛关注。实验和理论表明，材料的特性取决于材料的原子结构与微观结构[1]。尽管微观实验仪器扫描隧道显微镜和原子力显微镜的分辨率都已经达到原子尺寸量级，可以做到直接移动原子水平[2]，但目前要实现对裂纹尖端附近的变形和失效机理的动态观察仍很困难。随着计算机水平的发展，分子动力学模拟技术弥补了这一不足，可以展现材料在这一过程区的微观动态过程。

已有大量利用分子动力学方法对材料变形和失效过程中缺陷附近微结构演化机理的研究。Argon、Dienes等[3-4]在20世纪80年代就利用分子动力学模拟方法进行了微裂纹的扩展研究，但限于当时的计算水平，其重点研究了裂纹的扩展以及裂纹区域的脆-塑转变过程。随着计算水平的提高，研究体系的规模逐渐扩大，缺陷扩展过程中位错、相变、孪晶等微结构演化机制以及缺陷形式、载荷方式等对裂纹缺陷扩展机理的影响也逐渐被研究，并且得到了一些重要结论[5-8]。近年来，分子动力学研究也扩展到材料在疲劳载荷下失效过程的微观机制研究领域[9-11]，不过这方面的工作相对较少。

金属单质铁常温下以α-Fe形式存在，为体心立方bcc结构，因金属铁在结构中有着广泛的用途，学者们对其微观尺度上的失效和破坏机理做了大量的研究。但目前很多关于用分子动力学研究α-Fe的工作都仅仅考虑材料在某一特定晶向下的失效机理[12-13]，尽管曹莉霞等[14]用F-S多体势[15]模拟研究了沿几种典型晶体取向的α-Fe裂纹在外载作用下的形变及相关缺陷的形成和发展过程，但是作者没有考虑α-Fe在疲劳载荷作用下材料变形与失效的微观机理。而现实工况中，结构受疲劳载荷作用而失效的情况相当普遍，因而这一研究有着重要意义，Uhnáková等[16-18]研究了室温下带边裂纹单晶的α-Fe在Ⅰ、Ⅱ、Ⅲ型疲劳加载下，裂纹扩展和位错发射机理，但又没有考虑不同晶向的影响，对裂纹扩展过程中一些重要的现象也未详尽描述。

为了能更全面地理解材料的微观断裂行为,我们系统地建立了几种典型的α-Fe裂纹分子动力学模型，采用大规模分子动力学模拟程序LAMMPS[19]，全面系统地研究了预制初裂纹单晶α-Fe拉伸与疲劳破坏失效的微观机理，揭示了材料不同晶向对微裂纹扩展方式、位错形核与发射、孪晶、相变等微观过程的影响机制。本文主要报道(010)[101]型裂纹的破坏机制。

1模型和方法

标准的实验和理论工作都指出，体心立方铁的解理面是(100) 和(110)面，主要的滑移系是{110}〈111〉和{112}〈111〉[20-21]，为此，建立了4种不同取向的裂纹模型。对于一个特定的裂纹取向,用裂纹所在的平面和裂纹前沿方向这两个量来进行标定，即(裂纹所在平面)[裂纹前沿方向]的形式，本系列研究所取的4种裂纹构型分别为(010)[101]、(010)[001]、(0-11)[100]、(01-1)[011]，本文将针对(010)[101]型中心微裂纹的破环机制进行详细研究。

图1为模拟中所用的几何构型,a0为中心裂纹宽度，a0/w=0.05。W、H、t分别表示x、y、z三方向的模型尺寸。位移载荷沿y方向施加，在整个模拟过程中，将顶部和底部各1.25个晶格常数高度的原子在y方向刚化。x和z方向取为周期性边界条件，y方向取为非周期性边界条件。

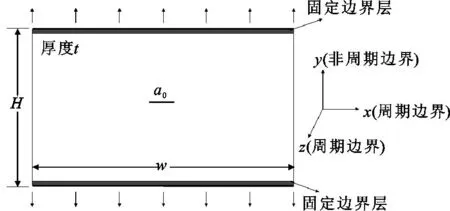
图1　模型几何构型

按图1建立α-Fe的4种分子动力学裂纹模型，其晶体取向与坐标轴对应关系为x:[10-1]；y:[010]；z:[101]。模型尺寸大小为W=32.43 nm，H=22.93 nm，t=2.03 nm，模拟体系原子总数达到128 800个。

原子间相互作用采用Mendelev[22]拟合的嵌入原子势，为了验证该势函数的可靠性，文章计算了α-Fe的一些重要物理量，并与实验和其他工作所获得的参数对比，如表1和表2所示。

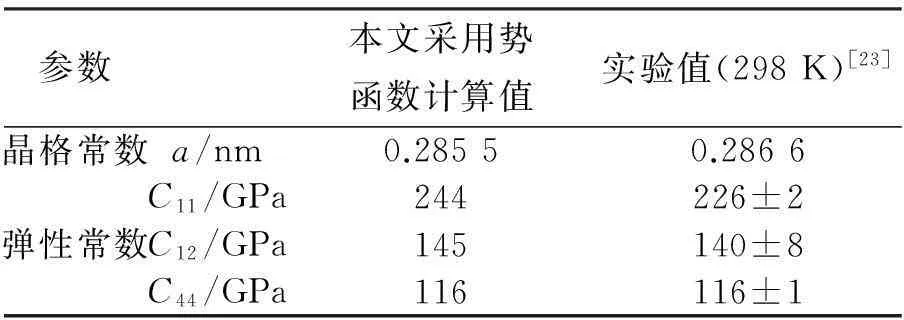
表1　晶格常数和弹性常数计算与实验值比较

通过Mendelev[22]势函数下的材料晶格常数和弹性常数与实验值的比较，表1表明，除C11以外，其他都符合的很好。表2还表明，与文献[20，24]一致，(110)和(100)面的表面能更小，(110)表面最小，最有可能成为α-Fe的最优解理面，符合实验规律[20-21]。该势函数在各项物理性能上有极高的可靠性，可以用于本文对α-Fe裂纹的拉伸和疲劳的变形与失效机制研究工作。

表2　α-Fe不同晶面的表面能

*本工作计算值。

模拟温度限制在100 K，时间积分步长取为0.001 ps，采用Velocity-Verlet算法求解运动方程。模拟开始前，对系统进行能量最小化并在NVE系综下弛豫，接着在NPT系综下，沿y方向上下对称地施加拉伸载荷以及拉伸和压缩载荷，以模拟产生拉伸荷载和循环荷载，整个模拟计算采用大规模分子动力学模拟程序LAMMPS[19]。为了尽可能接近实际加载情况，本文采用沿拉伸方向线性分配拉伸速度的方法，给模型施加需要的速度，如下图2a所示，模拟过程每隔200步统计记录相关数据。

在分子动力学计算中，基于计算效率的考虑，不宜采用较低的应变率，参考其他分子动力学模拟工作[25]，在模拟过程中给模型施加3×109s-1的应变率。加载过程如下：对模型首先进行单向拉伸，同时观察构型和应力应变的变化情况，以得到裂纹扩展的临界应变εcri，从而确定最大循环加载应变εmax，循环加载过程中，取最小应变与最大应变比例关系为εmin/εmax=0.75来确定εmin，然后，按图2b所示加载循环载荷，以模拟材料疲劳失效过程。

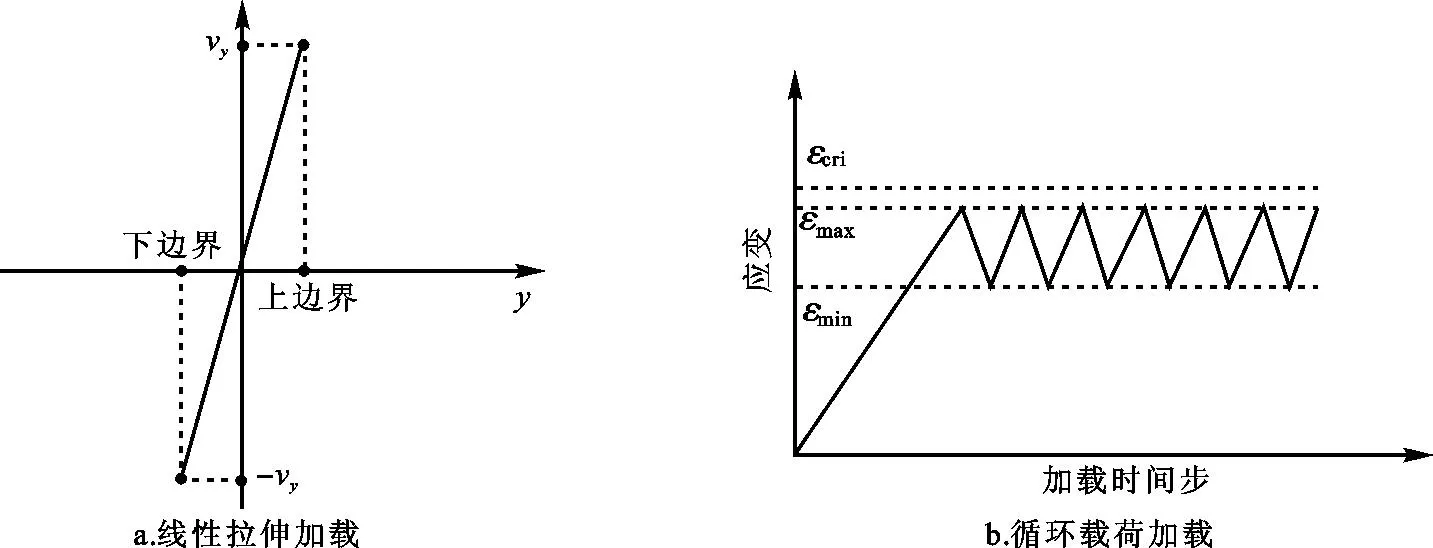
图2拉伸和循环加载示意图

Fig.2Schematic diagram of uniaxial tensile and fatigue loading研究发现各类裂纹构型扩展的临界应变和最大应变值与裂纹取向密切相关，差别较大。对于本文报道的(010)[101]裂纹，由于裂纹呈现严重钝化，所以无法确定其临界应变，多次试验后取εmax=0.062 98。

2模拟结果和分析

详细分析了预制(010)[101]中心裂纹单晶α-Fe在拉伸和循环加载两种典型外载荷下的变形与失效机理。

图3为(010)[101]裂纹构型拉伸时的应力-应变曲线和疲劳载荷下的裂纹长度与循环周次的关系，在后面所有的构型图中，我们的观察平面都取为x-y平面。

2.1单向拉伸下材料变形与失效机理分析

从图3a可以看出，拉伸过程中，曲线的变化形式丰富，因此材料破坏过程中必然包含重要的物理机制，而这些信息，也唯有通过原子尺度上的微观分析才能得到。

图3　载荷方向的拉伸应力-时间步关系(a)和裂纹长度与循环周次关系(b)

图4　(010)[101]裂纹拉伸过程典型时间步

如图4c当加载到22 500步时，滑移面上的原子堆垛顺序又发生变化，剪切带中的原子结构再次发生转变，逐渐转变回bcc结构，并出现孪晶现象，尽管此时裂纹仍在扩展，但应力下降速度明显减慢，接着图3a应力应变曲线中出现平台，此平台对应于加载过程中孪晶的出现，继续加载，伴随着孪晶的“扩展”，直到25 500步，剪切带中的孪晶基本转换完毕，裂纹钝化加剧，如图4d。此时图3a中应力曲线才继续下降。

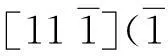
模拟结果与Ján Bosansky等[26]在实验中观察的现象一致,即α-Fe在变形与破坏过程中，裂尖层错和孪晶的形成是共同存在、相互伴随的过程，而且最终以孪晶变形为主，如图4e所示。

2.2循环载荷下的疲劳失效分析

图5　(010)[101]裂纹在各循环结束应变

由于在第一个循环中，就已经有变形孪晶出现，所以在以后的循环过程中，由于孪晶形变和位错的发射而使裂纹尖端的应力得到一定释放，裂纹缓慢平稳地发生塑性扩展扩展，见图3b。显然,孪晶的出现有利于减缓疲劳裂纹的开裂扩展速度。

3 结论

本文详细分析单晶α-Fe典型的(010)[101]裂纹构型在I型单向拉伸和循环载荷作用下的变形与失效微观机理，得到以下主要结论：

(1)具有(010)[101]裂纹的单晶α-Fe的拉伸破坏机理是一个以裂尖层错和孪晶形成共同存在、相互伴随的过程，而且最终以孪晶变形为主。

(3)具有(010)[101]裂纹的单晶α-Fe单向拉伸载荷作用时形成孪晶前还存在从bcc到fcc再到bcc的相变过程，而循环加载时α-Fe中直接形成孪晶结构。

因此α-Fe变形与失效的过程，是一个与裂纹方向、加载方式相关的位错、层错、孪晶和相变等多种微观机制共同作用的复杂过程。

参考文献:

[1] SHACKELFORD J F. Introduction to materials science for engineers[M]. New Jersey: Prentice Hall, 2004.

[2] EIGLER D M, SCHWEIZER E K. Positioning single atoms with a scanning tunnelling microscope[J].Nature,1990, 344(6266):524-526.

[3] ARGON A S, YIP S. Molecular dynamics simulation of crack tip processes in alpha-iron and copper[J]. Journal of Applied Physics, 1983, 54(9): 4864-4878.

[4] DIENES G J, PASKIN A. Molecular dynamic simulations of crack propagation[J]. Journal of Physics and Chemistry of Solids, 1987, 48(11): 1015-1033.

[5] ZHANG Y W, WANG T C, TANG Q H. Simulation of nucleation and emission of dislocations by molecular dynamics method[J]. Journal of Applied Physics, 1995, 77(6): 2393-2399.

[6] KUCHEROV L, TADMOR E B. Twin nucleation mechanisms at a crack tip in an hcp material: Molecular simulation[J]. Acta Materialia, 2007, 55(6): 2065-2074.

[7] QI H G, GUO Y F, TANG X Z, et al. Atomistic simulation of the structural evolution in magnesium single crystal under c-axis tension[J]. Acta Metallurgica Sinica(English Letters), 2011,24(6):487-494 .

[8] YUAN Y Q, CHEN H Y, ZENG X G, et al. MD simulation on evolution of micro structure and failure mechanism around interactional voids in pure Al[J]. Applied Mechanics and Materials, 2014, 444/445:183-190.

[9] CHANG W J, FANG T H. Influence of temperature on tensile and fatigue behavior of nano scale copper using molecular dynamics simulation[J]. Journal of Physics and Chemistry of Solids, 2003, 64(8): 1279-1283.

[10] POTIRNICHE G P, HORSTEMEYER M F, JELINEK B, et al. Fatigue damage in nickel and copper single crystals at nano scale[J]. International Journal of Fatigue, 2005, 27(10): 1179-1185.

[11] TANG T, KIM S, JORDON J B, et al. Atomistic simulations of fatigue crack growth and the associated fatigue crack tip stress evolution in magnesium single crystals[J]. Computational Materials Science, 2011, 50(10): 2977-2986.

[12] ANNA M， GLENN E B. Ductile-brittle behavior of (001)[110]nano-cracks in bcc iron[J]. Materials Science and Engineering A , 2004, 387:414-418.

[13] 吴映飞,王崇愚, 郭雅芳.体心立方铁中裂纹扩展的结构演化研究[J]. 自然科学进展，2005, 15(2):206-211.

[14] 曹莉霞,王崇愚. α-Fe 裂纹的分子动力学研究[J]. 物理学报，2007, 56(1): 413-422.

[15] FINNIS M W, SINCLAIR J E. A simple N-body potential for transition metals[J]. Philosphical Magazine A, 1984, 50(1): 45-55.

[19] PLIMPTON S J. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117(1): 1-19.

[20] 冯端.金属物理学[M]. 北京：科学出版社，1999.

[21] HU S Y, LUDWIG M, KIZLER P,et al. Atomistic simulations of deformation and fracture of α-Fe[J]. Modelling and Simulation in Materials Science and Engineering, 1998, 6(5): 567 - 586

[22] MENDELEV M, HAN S, SROLOVITZ D, et al. Development of new interatomic potentials appropriate for crystalline and liquid iron[J]. Philosophical Magazine, 2003, 83(35): 3977-3994.

[23] LEESE J, LORD A E J. Elastic stiffness coefficients of single-crystal iron from room temperature to 500 ℃[J]. Journal of Applied Physics, 1968,39(8):3986-3988.

[25] POTIRNICHEA G P, HORSTEMEYERA M F, JELINEKA B, et al. Fatigue damage in nickel and copper single crystals at nano scale[J]. International Journal of Fatigue, 2005, 27(10):1179-1185.

〔责任编辑 李博〕

Atomistic simulation of failure mechanism for α-Fe with central crack under uniaxial tensile and fatigue loading

YUAN Yuquan1， ZENG Xiangguo2, HU Yanfei1

(1 School of Science, Sichuan University of Science & Engineering, Zigong 643000, Sichuan, China;2 College of Architecture and Environment, Sichuan University, Chengdu 610065, Sichuan, China)

Abstract:Molecular dynamics simulation is performed for the failure mechanism for α-Fe with (010)[101] centered pre-crack defect under uniaxial tensile and fatigue loading. The results show that the failure mechanism under uniaxial tensile loading is a process with crack blunting, stacking faults and twins formation. While under fatigue loading, the failure mechanism is twins deformation based, coupled with dislocation, partial dislocation, stacking faults.Furthermore the twin deformation occurs easier than the dislocation emission in [11-1](-121) slip system. The study indicate that the deformation and failure process of α-Fe with crack defect is a complicated process, which is the result that many mechanisms act together, such as dislocation, stacking faults, twin and phase transition.

Keywords:molecular dynamics simulation; central crack; α-Fe; tension; fatigue

中图分类号:O483

文献标志码:A

基金项目：国防重点基金(B1520132013-1); 四川理工学院科研项目(2015RC41;2015RC44); 四川省教育厅科研项目(15ZB0207)

收稿日期：2015-08-01

doi:10.15983/j.cnki.jsnu.2016.02.221

文章编号：1672-4291(2016)02-0021-06

第一作者： 袁玉全，男，副教授，博士，研究方向为计算固体力学和原子分子物理。E-mail：yuquan_yuan@suse.edu.cn