基于CDSC的APF锁相环设计

上海电力学院电气工程学院 温华生



基于CDSC的APF锁相环设计

上海电力学院电气工程学院 温华生

【摘要】本文提出了一种基于级联型延迟信号消除（CDSC）的锁相环技术（CDSC-PLL），该锁相环克服了传统dq锁相环在电网电压畸变或不对称时存在较大稳态误差的缺点。CDSC-PLL是在传统dq锁相环的控制环节中加入了一个CDSC环节，即dq_CDSC_PLL，文章对所提锁相环进行了理论分析和公式推导。通过仿真验证了所提锁相环理论的正确性及可行性。

【关键词】锁相环；级联型延迟信号消除

0 引言

近年来，随着大量电力电子装置的广泛应用，其非线性的工作特性将产生大量谐波和无功功率注入电网，造成电能质量下降，然而，很多高精度以及计算机系统等敏感性负载对电能质量的要求越来越高，因此电力系统谐波抑制以及无功补偿问题成为研究的热点，静止无功功率发生器、有源电力滤波器（Active Power Filter，APF）以及统一电能质量调节器因其优越的谐波抑制和无功补偿性能被广泛应用。

锁相环技术[1-6]对于APF来说至关重要，因为在谐波检测以及指令电流计算时需要实时、准确的电网电压相位信息，锁相环的动态响应速度以及稳态精度直接影响APF的整体性能，因此，研究一种在电网电压普遍存在谐波、波动以及不对称的情况下，能够实时准确的获取电网电压相位的锁相环技术具有重要意义。

1 基于dq变换的锁相环原理

将三相电网电压向量经Clarke变换使其由三相静止坐标系变换到两相静止坐标系中，假设归一化后的标准三相电压表达式如下：

通过静止坐标变换，将三相电压由三相静止坐标系变换到两相静止坐标系中，坐标变换如下：

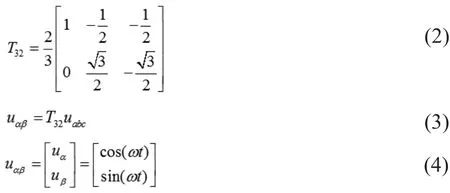
其中，T32为Clarke变换的变换矩阵，然后再由两相静止坐标系变换到两相旋转坐标系，坐标变换如下：

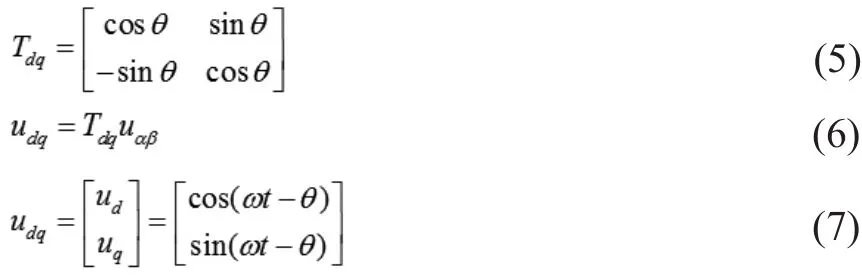
由图1中可以看出，可通过控制三相电压合成矢量uabc在q轴上的投影uq来跟踪电网相位。当uq>0时，d轴滞后uabc，此时应增大dq坐标系的旋转角频率；当uq<0时，d轴超前uabc，此时应减小dq坐标系的旋转角频率；当uq=0时，d轴和uabc重合，此时d轴和uabc同相位。因此，只要控制三相电压合成矢量在q轴上的投影uq使其为零即可完成鉴相。

图1 旋转坐标变换

基于dq变换的三相锁相环（dqPLL）结构图如图2所示：

图2 基于旋转坐标变换的三相电压锁相环结构图

其中abc/αβ、αβ/dq以及sinθ/cosθ共同组成鉴相器(PD)模块。该锁相环系统中环路滤波器(LPF)的作用是消除鉴相器(PD)输出信号中的高频噪声信号，然后将环路滤波器(LPF)输出的控制信号送给压控振荡器(VCO)，由于送入压控振荡器的控制信号多为低频信号，所以环路滤波器具有低通特性，本文采用的环路滤波器是一个一阶比例积分器。环路滤波器(LPF)输出的控制信号经过压控振荡器(VCO)后转换成频率，但是，在锁相环系统中，压控振荡器(VCO)需要输出的是相位，因此本文将积分器1/s作为压控振荡器(VCO)，对频率进行积分得到相位。

当电网电压对称不畸变时，dqPLL响应速度快，精度高，稳态误差小，但是，当电网电压畸变和不对称时，dqPLL存在比较大的稳态误差，针对这个问题，在dqPLL的基础上提出一种基于延迟信号消除的锁相环技术。

2 基于延迟信号消除（DSC）的锁相环设计

2.1 基于延迟信号消除的锁相环原理

通过谐波的半波对称性在dq坐标系中将谐波消除，也即延迟信号消除（DSC）法，将输入的谐波信号延迟正序基波信号周期T的1/n倍，然后取原信号和延迟信号和的平均值作为输出，其数学表达式如下：

其中，T为正序基波分量的周期。

在dq坐标系中延迟信号消除（DSC）的具体过程以及在dq坐标系中d轴的h次谐波在时域内的表达式如下所示：

则：

同理，在dq坐标系中q轴的h次谐波也作类似的运算，则dq坐标系的h次谐波经过延迟信号消除后，其表达式如下：

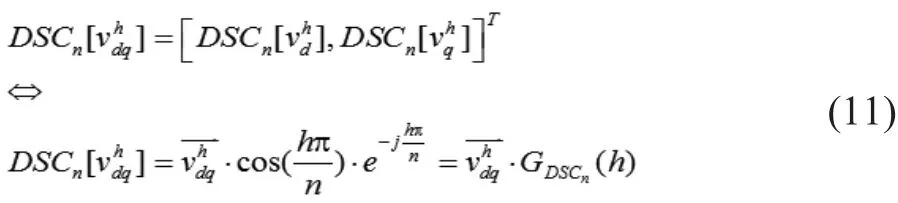
由此可得基于延迟信号消除的锁相环（dq_DSC_PLL）原理图如下所示：

图3 dq_DSC_PLL的原理

由式(12)可知，当n=4且k分别取0，1，2时，在dq坐标系中h的值分别为-2，2，-6，6，-10，10，-14，14，-18，18，对应在abc三相坐标系中h的值分别为-17, -13，-9，-5，-1，3，7，11，15，19即在dq坐标系中，对d轴和q轴信号延迟1/4个正序基波周期，仅能消除三相系统中部分正序谐波分量和负序谐波分量，因此，当电网电压畸变时，仅有一个信号延迟消除模块，并不能够消除全部谐波，锁相环仍然存在稳态误差。

2.2 基于级联延迟信号消除的锁相环（dq_CDSC_PLL）技术

由上式(12)可知，虽然k的取值多样，但是一个n值只对应有限个h值，同时，由式(11)可以得出这样一个结论，延迟信号消除模块的增益和信号频率无关，并且增益总小于1，换言之，某一次谐波不能被完全消除时也会被衰减，除此之外，延迟信号消除模块并不会改变信号的频率，因此，可以将多个取不同n值的延迟信号消除模块串联在一起，组成一个级联型延迟信号消除模块。

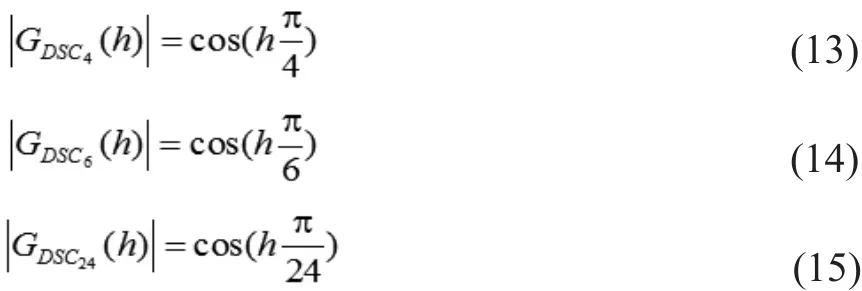
将其级联后的模块可表示为：

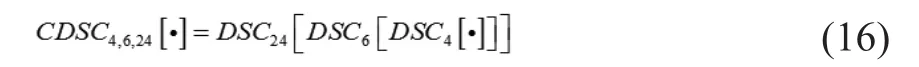
级联模块的增益为：

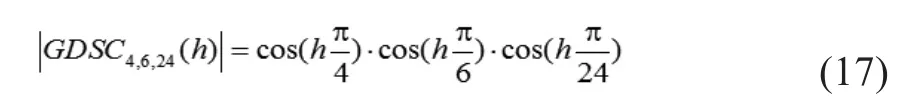
在dq坐标系中，h为正负序2,3,6,9,10,12,14,15,18次谐波，在abc坐标系中，h为正序3, 4, 7, 10, 11, 13, 15, 16, 19次以及负序1,2,5,8,9,11,13,14,17次谐波。

当n分别取2,4,8,16时组成的级联模块增益为：

在dq坐标系中：h为正负序1,2,3…..14,15,17,18次谐波，相对应在abc坐标系中：h为直流分量，负序1次、2次，以及正负序2,3,4….15,16,18次谐波。

从上面的计算结果可以得出这么一个结论，即通过选取不同的n值，将几个不同的延迟信号消除模块进行组合级联，可以选择性的消除谐波，同时，间谐波也会被不同程度的衰减，如果某一特定的间谐波需要消除，可以针对该间谐波重新选取一个n值构造一个延迟信号消除模块，并和原来的模块级联。基于级联延迟信号消除的锁相环（dq_CDSC_PLL）（n取2,4,8,16）原理图如图4 所示：

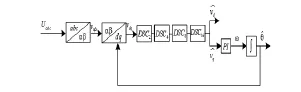
图4 基于级联延迟信号消除的锁相环原理

由上图4基于延迟信号消除的锁相环原理可知，每个DSC模块都是在对原信号进行延迟1/n个正序基波信号的基础上进行谐波消除的，每个模块都可以消除一定次数的谐波，将模块级联在一起，即可将常见谐波基本消除，从而提高锁相环的锁相精度以及动态响应速度。

图5 电压不对称时各锁相环锁定的频率波形图

图6 电压含谐波时各锁相环锁定的频率波形图

3 仿真研究

通过以上对普通dq_PLL，延迟信号消除（DSC）法以及dq_CDSC_PLL的理论分析可知，基于CDSC的锁相环在电网电压不对称或者含有谐波时其锁相精度以及动态响应速度均高于普通dq_PLL，接下来对上述两种锁相环在MATLAB平台进行仿真验证。

（1）电压不对称时各锁相环锁定的频率仿真结果如图5所示。

（2）电压含谐波时各锁相环锁定的频率仿真结果如图6所示。

从图5及图6可以很直观的看出，电压不对称以及电压含谐波时对dq_CDSC_PLL的影响很小，而普通锁相环在这种情况下依然存在比较大的稳态误差，因此，仿真结果表明，在电压含谐波或者电压不对称时，较普通锁相环而言，本文所采用的基于CDSC的锁相环具有明显的优势。

4 结论

通过详细的理论分析以及最后的仿真实验结果表明，较普通锁相环而言，本文所提的锁相环技术在电网电压畸变或者不对称时，具有明显的优越性，在APF技术中，通过该锁相环可以获得更加准确、实时的电压相位信息，从而提高APF的补偿性能。

参考文献

[1]李明,王跃,方雄,等.无正交虚拟信号生成的单相DQ锁相环研究[J].中国电机工程学报,2011,31(15):27-32.

[2]KARIMI G M,IRAVANI M R.A method for synchronization of power electronic converters in polluted and variable-frequency environments[J].IEEE Trans.on Power Systems,2004,19(3):1263-1270.

[3]Y.F.Wang,Y.W.Li.Grid synchronization PLL based on cascaded delayed signal cancellation[J].IEEE Trans.Power Electron.,2011,26(7) :1987-1997.

[4]J.Svensson,M.Bongiorno,A.Sannino.Practical implementation of delayed signal cancellation method for phase-sequence separation[J].IEEE Trans.Power Del.,2007,22(1):18-26.

[5]吉正华,韦芬卿,杨海英.基于dq变换的三相软件锁相环设计[J].电力自动化设备,2011,31(4):104-107.

[6]KARIMI G M,IRAVANI M R.A method for synchronization of power electronic converters in polluted and variable-frequency environments[J].IEEE Trans on Power Systems,2004,19:1263-1270.

[7]RODRIGUEZ P,LUNA A,CIOBOTAIU M,et al.Advanced grid synchronization system for power converters under unbalanced and distorted operating conditions[C].//Proc of the 32st Annual Conference of the IEEE Industrial Electronics Society,IECON,2006:5173-5178.

[8]吕振林,田岚.基于一种新型自适应滤波的谐波检测算法[J].电力系统及其自动化学报,2007,19(5):75-78

[9]ABABNEH J I,BATAINEHM H.Linear phase FIR filter design using particle swarm optimization and genetic algorithms[J].Digital Signal Processing,2008,18(4):657-668.

[10]KARIMI-GHARTEMANI M,and IRAVANI M R,A Nonlinear Adaptive Filter for Online Signal Analysis in Power Systems:Applications[J].IEEE Transactions on Power Delivery,2 002,17(2):617-622.

[11]GONG Y and COWAN C F N,A novel variable tap-length algorithm for linear adaptive filters[C].in Proc.IEEE Int.Conf.Acoustics. Speech,Signal Process.,Montreal,QC,Canada,May 2004.

[12]QU Yanbin,MENG Fanggang,GAO Lei.A New Variable Step Size LMS Adaptive Filtering Algorithm[C].International Society for Industrial Ecology.Vigo,Spanish,2007:1601-1605.

[13]LI Ning,ZHANG Yonggang,ZHAO Yuxin,et al.An improved variable tap-length LMS algorithm[J].IEEE Transactions on Signal Processing,2009,89(5):628-631.

温华生（1989—），江西宜春人，硕士研究生，研究方向：三相四线制有源电力滤波器的控制策略研究。

作者简介：