基于承灾载体单体脆弱性的区域脆弱性研究*

姚思敏，钟少波，黄全义

(清华大学 工程物理系，公共安全研究院，北京 100084)



基于承灾载体单体脆弱性的区域脆弱性研究*

姚思敏，钟少波，黄全义

(清华大学 工程物理系，公共安全研究院，北京 100084)

摘要:为了从区域宏观层面与承灾载体个体层面对脆弱性进行量化，从考量承灾载体的个体属性入手建立了单体脆弱性计算模型。以此为基础，通过分析单体脆弱性与区域脆弱性的关系，并引入区域脆弱性综合影响系数以反映自然环境和社会经济等系统性因素的影响，建立了区域脆弱性计算模型。以华北某区县暴雨灾害区域脆弱性评估为例对该计算模型的实际应用进行阐述。

关键词:承灾载体；单体脆弱性；区域脆弱性；模型；综合影响系数

纵观目前国内外学者关于承灾载体脆弱性的研究成果，脆弱性评估工作多为单一地区单一灾种的分析，大部分指标不统一，可比性较差，缺少跨区域多灾种适用的评价方法[1-13]。同时，关于承灾载体个体的脆弱性如何反映在区域整体的脆弱性，单体脆弱性与区域脆弱性的定性、定量关系，自然、社会等系统因素如何影响区域脆弱性，鲜少有研究者尝试讨论并开展工作。事实上，单体脆弱性是形成区域脆弱性的必要条件，两者之间存在内在的关系。同时，单体本身的脆弱性及其存在的背景条件和环境、单体之间的空间分布结构等因素决定了区域脆弱性不是单体脆弱性在空间上的简单叠加，而是诸多复杂因素导致的综合效应。

本文基于上述认知逻辑，首先对单体脆弱性进行研究，提出了一种基于灾害相关承灾载体特征属性的脆弱性计算方法。在此基础上，分析单体脆弱性与区域脆弱性的关系，并引入区域脆弱性综合影响系数，建立了区域脆弱性计算模型。本文通过华北某个区县暴雨灾害脆弱性研究实例，对该计算模型的实际应用进行阐述。结果表明，本文提出的区域脆弱性计算模型符合实际，有较好的应用价值，为科学评估灾害风险、提高抗灾应急能力提供了一种新的思路和方法。

1承灾载体单体脆弱性计算

单体是承灾载体层面的最小评估单元。基于承灾载体自身的属性特征，从挖掘承灾载体个体信息入手进行单体脆弱性定量评估，首先需要根据评估区域确定脆弱性集成信息表，以对区域内所有承灾载体的脆弱性有系统的表达。

定义1S=(R,U,A,V)为评估区域的脆弱性集成信息表，其中R={r1,r2,r3,…rn}是关于所考察灾害种类的非空有限集合。由于本文不考虑多灾种耦合情形下的承灾载体脆弱性，R默认为单元素集合，即R={r}。U={u1,u2,u3,…，un}为灾害影响区域内所有承灾载体的非空有限集合。A是脆弱性属性集合，a是集合A中的脆弱性属性元素。V是脆弱性属性元素a的取值集合。

在脆弱性信息表S中，脆弱性属性集A由分量属性集C和判定属性集D组成，并且满足C∪D=A,C∩D=φ。

脆弱性分量属性集C={a1,a2,a3,…，an}中的元素是计算某一承灾载体单体脆弱性时的分量指标。比如考虑建筑物在暴雨灾害影响下的脆弱性，需要考虑它的结构选型、建筑材料、设计年限及使用时间、防水层、地基状况等因素；考虑人在台风灾害影响下的脆弱性，需要考虑其年龄与身体状况、应急心理素质与受遮蔽程度等因素，这些因素就是承灾载体单体脆弱性分量属性。脆弱性分量属性集C与承灾载体对象集U中的元素分别可以是多对一、一对多的关系。即一个承灾载体对象对应多个脆弱性分量属性，而一个脆弱性分量属性可以被多个承灾载体共享。

脆弱性判定属性集D中的元素与承灾载体集合U中的元素一一对应，即一个承灾载体只有一个脆弱性判定属性，表征待考察的承灾载体是否会受灾害r的影响而导致损失。D×V→Vad,其中Vad是判定属性取值集合，vad为其对应的0/1二值元素。例如，由实际经验可知，发生干旱灾害时，农作物极易受影响而产生损失，其脆弱性判定属性取值vad为1，而房屋不易受干旱影响，其判定属性取值vad为0。即有：

(1)

因此，针对某一承灾载体u，其脆弱性属性集合为Au={ad,a1,a2,a3，…，an}，相对应的脆弱性属性取值集合为Vu={vad,va1,va2,va3，…，van]。

定义2Θ为求取灾害r作用下表现脆弱性的承灾载体的判定算子，作用于如下的判定方程：

(2)

定义3F为灾害r的承灾载体脆弱性信息提取函数，

(3)

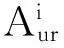
结合专家意见、历史灾情等考察各个脆弱性分量属性，将承灾载体在每项分量属性上可能的表现分为三个等级，分别赋值1、2、3。即

vai=1或2或3，i=1,2,3…n 。

(4)

其中，越易受损害时得分越高，反之越低。即得分为1的灾害情形下最不脆弱，得分为3的灾害情形下最为脆弱，即最容易发生灾损。

至此，关于待评估的承灾载体，计算其单体脆弱性的全部信息已经得到。通过实地考察承灾载体确定各项脆弱性分量属性取值后，其单体脆弱性值计算如下：

(5)

式中：vai是承灾载体脆弱性分量属性取值，n是分量属性的个数，tu是承灾载体单体脆弱性值，0≤tn≤1。图1展示了承灾载体单体脆弱性的计算流程。

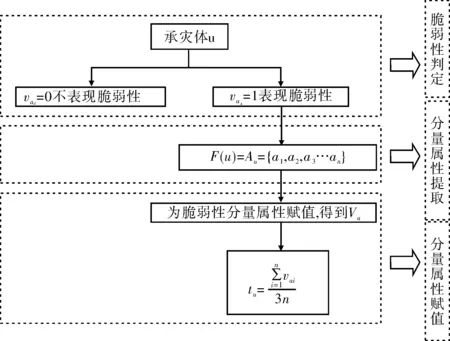
图1　承灾载体单体脆弱性计算流程

2基于承灾载体单体脆弱性的区域脆弱性计算

本章以承灾载体单体脆弱性的计算为基础，围绕区域脆弱性综合影响系数，单体脆弱性与区域脆弱性的关系等，对区域综合脆弱性的计算进行研究。

2.1区域脆弱性综合影响系数计算

自国际灾害学界开始关注人类经济社会系统在面对灾害时呈现脆弱性的几十年中，众多学者和机构对脆弱性的内涵与定义进行过阐释[14-18]。虽然到目前为止仍然没有公认的关于脆弱性定义的确切描述，但一个普遍的共识是：一个地区的脆弱性不仅受其中承灾载体单体的物理化学性质影响，同时还受社会经济和自然环境等承灾系统结构性因素影响。因此，提出区域脆弱性综合影响系数μ，反映区域的水文、地形、植被等自然条件和经济发展与应急管理水平等社会条件对区域脆弱性的影响。μ应该是一个1左右的修正性系数。μ大于1时，表示自然、社会等系统结构性因素加重了区域脆弱性，且这种不利影响越严重，μ的取值越大。反之，μ的取值小于1时，表明有利的自然和社会因素减少了承灾载体受损的可能性，减弱了区域脆弱性。

采用指标体系法确定区域脆弱性综合影响系数μ的取值。首先，根据专家经验或历史灾情进行指标的选取。其次，将所有指标根据其对区域脆弱性的正、负相关性分为两组。当指标值越大越能加剧区域脆弱性时，指标是正相关的；当指标值越大越能削弱区域脆弱性，使其不易受灾损时，指标是负相关的。对于正、负两组指标，分别采用以下算式进行标准化：

(6)

式中：xi、xj分别是正指标i和负指标j的标准化值，xi0、xj0是它们的初始值，xi max、xi min、xj max、xj min分别是正指标i和负指标j的最大样本值和最小样本值。

指标权重的确定可以采用AHP层次分析法、模糊评价法、灰色关联度分析等。为了使得影响系数μ体现其对区域整体脆弱性状况的修正和调整意义，将各指标的标准化值乘以对应的权重后加1。则区域脆弱性综合影响系数μ为：

(7)

式中：ωi、ωj分别是正、负指标xi、xj的权重。

2.2基于单体脆弱性的区域脆弱性计算

区域脆弱性指的是区域内由承灾载体的单体脆弱性及自然、社会等系统性因素造成区域易受灾损的性质。考虑到实际工作中区域内承灾载体的难以遍历性，为了以有限的承灾载体样本得到整个区域脆弱性信息，需要做以下两个假设。

假设1在区域整体层面上，所有承灾载体以其中心点所在位置被简化为一个点。

假设2空间上有重合或包含关系的多个承灾载体的单体脆弱性值等于其中脆弱性最低的承灾载体的单体脆弱性值。

在大尺度空间范围区域脆弱性评估中，根据这两条假设，所有承灾载体不论实际形状、大小均近似以点的形式分布在区域内，当考虑人处在建筑物内而受到遮蔽等多个承灾载体在地理位置重合或包含的情形时，取不易受损的承灾载体的tu为此点的脆弱性值。

基于已知的区域脆弱性综合影响系数，为了从有限的n个承灾载体单体脆弱性值和它们的空间分布结构推知区域脆弱性的情况，考虑脆弱性在区域范围内是否可以被近似为连续分布，分以下两种情况讨论。

2.2.1脆弱性在区域范围内近似连续分布

脆弱性在区域内近似连续分布是一种较为理想且罕见的情形，当脆弱承灾载体在区域内密集分布且性质相近时，“连续分布”的近似可以成立。此时采用插值的办法以“窥几斑，知全豹”。

插值是一种通过已知离散点集的约束，求取定义在连续集合的未知连续函数从而达到获取整体规律的目的的一种函数逼近或数值逼近方法。不同于拟合只反映大致趋势，插值要求表达式或曲面全部经过已知样本点。因此，在脆弱性近似连续分布时，插值的方法能够最大程度地基于已知的承灾载体单体脆弱性基础数据求取区域整体脆弱性分布状况。

数学软件Matlab中的二维插值函数interp2是可行的实现工具。构建一个xyz三维空间，其中xy轴表征待评估区域的地理坐标，z轴为每个点对应的脆弱性值tui。Interp2函数的应用格式如下：

zi=Interp2(x,y,z,xi,yi,method) 。

式中：x,y,z是原始数据，返回的函数值zi是(xi,yi)根据插值函数计算得到的结果，method是插值方法。

图2是插值过程的一个示例。插值曲面突起的区域代表评估区域内脆弱性比较高的部分，比如幼儿园、小学等孩童高密度聚集地，低矮平房、危房为主要建筑形式的老城区等区域。这些高脆弱性区域是灾害风险评估需要着重考察的地区，也是防灾减灾和应急管理重点工作对象。密度曲面低凹的区域代表评估区域内脆弱性比较低的部分，比如摩天楼集中的商业区等。

将由n个原始数据点插值得到的曲面命名为区域脆弱性趋势曲面，其表达式z=f(x,y)。则区域脆弱性值可由以下计算式得出：

(8)

式中：μ是区域脆弱性综合影响系数，S是评估区域Φ的总面积，z=f(x,y)是插值得到的曲面表达式，T是区域脆弱性值。

图2　插值示例

2.2.2脆弱性在区域范围内不连续分布

由图1［2］可知，在喷氨量一定的条件下，SNCR理论脱硝效率可达90%，但是在实际的运行过程中，由于炉膛内温度分布不均、炉膛负荷波动以及还原剂与烟气无法保证完全混合等因素影响，SNCR系统在工程应用中，氨逃逸控制在8 mg/m3以内，SNCR脱硝效率为40%～60%。

脆弱性在区域范围内不连续分布是一种更为常见的情形，这意味着区域内脆弱承灾载体分布不足够密集，或者有较大量的单体其脆弱性值大于或者小于周围所有的点使得整体不能近似为连续分布。此时，直接由已知承灾载体的单体脆弱性加权平均推得区域整体基于承灾载体的脆弱性。其中权重反映承灾载体对于区域整体脆弱性状况的重要性程度。当承灾载体自身的脆弱性对周围承灾载体有重大影响或承担重要的社会功能时，其权重较大。反之较小。则区域脆弱性性计算如下：

(9)

式中：tui是已知的承灾载体单体脆弱性值，ωi是其重要性权重系数，n是已知样本单体个数，T是区域脆弱性值。

图3展示了计算区域脆弱性的综合流程。

图3　区域脆弱性计算综合流程

3暴雨灾害区域脆弱性研究实例

选取华北平原某区县F(115°25’~116°15’E,39°30’~39°55’N)作为评估区域，以暴雨灾害为背景，进行区域脆弱性的实例研究。研究区域F下辖6个街道、7个乡、13个镇，地形变化复杂，且夏季常遭受暴雨灾害侵袭，南北部承灾载体分布状况差异较大，具有一定的研究意义。实例首先以街道A为独立的评估单元展示如何计算承灾载体单体脆弱性及街道A的区域脆弱性，再由此推广到其他的街道、乡镇并给出区域F整体的脆弱性区划图。

3.1街道A暴雨灾害区域脆弱性分析

首先以街道A内的一幢写字楼u为例计算承灾载体单体脆弱性。对于房屋类承灾载体来说，受暴雨灾害时vad=1，由脆弱性信息提取函数可知写字楼u的脆弱性分量属性分别为使用时间、结构选型、建筑材料和防水层等因素。通过实地考察，根据各项脆弱性分量属性的赋值标准，得出以下承灾载体单体脆弱性计算表(表1)。因此，这幢写字楼的单体脆弱性为：

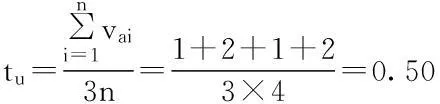
(10)

通过暴雨灾害脆弱承灾载体集合判定方程得知街道范围内受暴雨灾害影响的承灾载体多达数百处。因条件所限，选取居民楼、办公楼、立交桥、变压站、通信基站等易受暴雨影响的主要承灾载体共93处，分别对这些样本承灾载体进行考察并归为房屋类承灾载体、电力通讯基础设施类承灾载体和道桥类承灾载体等三大类承灾载体以简化计算(图4)。考虑到承灾载体样本个数不足够多且分布零散，区域内脆弱性不满足近似连续分布的条件，因此不采用插值的办法进行处理。假定所有承灾载体的重要程度相同，对样本承灾载体的脆弱性求取平均值得到街道A的承灾载体单体脆弱性平均值为0.62。

图4　A街道样本承灾载体分布图

区域脆弱性综合影响系数由自然环境和社会经济两方面多因素共同决定。根据地形等自然环境特点，结合人均GDP、应急能力等社会经济指标，计算街道A区域综合脆弱性影响系数(表2)。

表2　街道A区域脆弱性综合影响系数分项指标表

依据现有基础数据和专家意见得出各项指标初始值，对正、负相关指标分别进行标准化，用AHP层次分析法得出各指标的权重，则区域脆弱性综合影响系数计算如下：

(11)

得出街道A区域综合脆弱性影响系数为1.08。

T=μ·t=1.08×0.62=0.67 。

(12)

因此A街道的区域脆弱性为0.67。

3.2区域F暴雨灾害区域脆弱性分析及区划

研究区域F下辖共26个街道、乡镇。西北部是山地、丘陵，因此房屋、路桥基础设施等承灾载体分布较为稀疏，东南部为沃野平原，承灾载体分布密度较大。根据各个乡镇、街道的脆弱承灾载体分布数量和特点，结合历史灾损情况，分别选取80~150个易受暴雨灾害的承灾载体单体进行脆弱性计算形成单体脆弱性样本库。面积较小，承灾载体样本点分布较为密集、均匀的乡镇或街道采用插值的办法求取区域脆弱性值，否则采用加权平均的办法计算区域脆弱性值。结合区域综合脆弱性影响系数分析，得到各个乡镇街道的区域综合脆弱性值分布状况。在GIS中进行脆弱性值的标示得到区域F暴雨灾害综合脆弱性区划图(图5)。

图5　区县F暴雨灾害区域脆弱性区划图

3.3分析与讨论

以华北平原某区县F为研究对象进行暴雨灾害情形下区域综合脆弱性分析。依据各乡镇、街道脆弱性分布状况与脆弱性区划图，结合暴雨灾害历史灾损情况，做以下两点讨论。

(1)区域中部、东部和南部位于华北平原，西部和北部分别地处太行山脉和燕山山脉。因此人口密集、经济较为发达的乡镇多集中在中部和东南部，这些乡镇的承灾载体脆弱性相对西北部而言也更低。同时，在暴雨灾害情形下，西北部山地、丘陵等不利地形加大了滑坡、山洪、泥石流等次生灾害发生的可能性，反映在较大的区域综合脆弱性影响系数进一步放大了区域整体的脆弱性。从脆弱性区划图中可以看出，位于西北部的乡镇暴雨灾害脆弱性明显高于位于中部或者东南部的乡镇、街道，它们是防灾减灾和应急管理部门应当重点关注的地区。

(2)本文提出的基于承灾载体单体的区域综合脆弱性计算方法不要求遍历区域内的承灾载体。在实例研究中，受条件所限各个区县只取了较为有限的脆弱承灾载体样本，因此可能与真实的脆弱性状况有一定程度的偏差。实际应用时，脆弱承灾载体样本的选取应当尽可能大量且具有代表性，对区域综合脆弱性影响系数的分项指标考虑全面，才能较为真实地反映区域整体的脆弱性状况。

5结论

本文从分析单体脆弱性和区域综合脆弱性的含义出发，认为单体脆弱性的计算应该基于承灾载体个体属性的研究；区域综合脆弱性不仅来源于区域内的承灾载体，还受自然环境和社会经济等因素的影响，由此以承灾载体单体脆弱性为基础，引入区域综合影响系数，得出了区域综合脆弱性的计算模型。

为了验证计算模型的合理性，本文以华北平原某区县F作为研究区域展示在暴雨灾害情形下如何计算单体脆弱性及区域脆弱性，并给出了脆弱性区划。分析结果表明，基于承灾载体单体的区域脆弱性计算模型合理可行，并且对科学地防灾减灾具有一定的指导意义。

承灾载体脆弱性分析是风险评估的重要组成部分。国内外学者在脆弱性的分析方法与技术手段等方面的研究仍未达成共识。本文在现有研究成果的基础上，做了一些积极的尝试。如何从承灾载体出发更加全面地评估区域整体的脆弱性，如何评估多灾种耦合等复杂情形下区域整体的脆弱性，将会是未来主要的工作方向。

参考文献:

[1]贺帅，杨赛霓，李双双，等. 自然灾害社会脆弱性研究进展[J].灾害学,2014,29(3):168-173.

[2]石勇.灾害情景下城市脆弱性评估研究——以上海市为例[D].上海:华东师范大学,2010

[3]唐波,刘希林,尚志海.城市灾害易损性及其评价指标[J].灾害学,2012,27(4):6-11

[4]尹占娥,暴丽杰,殷杰.基于GIS的上海浦东暴雨内涝灾害脆弱性研究[J].自然灾害学报,2011,20(2):29-35.

[5]郭凤清，曾辉，丛沛桐，等. 潖江蓄洪区洪灾承灾载体 脆弱性分析[J].灾害学, 2014,29(3):102-107.

[6]谢梦莉.气象灾害风险因素分析与风险评估思路[J].气象与减灾研究,2007,30(2):57-59.

[7]于文金，赵景旺. 唐山市暴雨特征及风险评估分析研究[J]. 灾害学,2013,28(4):50-54.

[8]王静爱，商彦蕊，苏筠.中国农业旱灾承灾载体脆弱性诊断与区域可持续发展[J].北京师范大学学报:社会科学版,2005,13(3):130-137.

[9]陈香.台风灾害脆弱性评价与减灾对策研究——以福建省为例[J].防灾科技学院学报,2008,10(3):18-22.

[10]Moss R H, Brenkert A L, Malone E L. Vulnerability to climate change:a quantitative approach[R]. Technical Report PNNL-SA-33642, Pacific Northwest National Laboratories, Richland,WA,2001.

[11]Cutter S L. The Vulnerability of Science and the Science of Vulnerability[J]. Annals of the Association of American Geographers, 2003, 93(1):1-12.

[12]史培军.灾害研究的理论与实践[J].南京大学学报:自然科学版,1991(自然灾害研究专辑):37-42.

[13]史培军.再论灾害研究的理论与实践[J].自然灾害学报,1996,5(4):6-17.

[14]Turner B L, Kasperson R E. A framework for vulnerability analysis in sustainability science[J]. Proceedings of the National Academy of Sciences of the United States of America, 2003, 100(14):8074-8079.

[15]Matthew M.Fontaine,Anne C. Steinemann. Assessing vulnerability to natural hazards:Impact-Based method and application to drought in Washington State[J]. Natural Hazards Review, 2009, 10(1):11-18.

[16]Khanduri A C,Morrow G C.Vulnerability of buildings to windstorms and insurance loss estimation[J]. Journal of Wind Engineering and Industrial Aerodynamics,2003,91(1): 455-467.

[17]葛全胜，邹铭，郑景云. 中国自然灾害风险综合评估初步研究[M]. 北京：北京出版社，2008.

[18]Gallopin G C. Linkages between vulnerability,resilienc and adaptive capacity[J]. Global Environmental Change,2006,16(2): 293-303.

A Study on Regional Vulnerability Based on Single-object Vulnerability of Disaster-affected Objects

Yao Simin, Zhong Shaobo and Huang Quanyi

(InstituteofPublicSafetyResearch,TsinghuaUniversity,Beijing100084,China)

Abstract:In order to evaluate vulnerability from different perspectives, we discuss about how to conduct quantitative assessment of both regional vulnerability and single-object vulnerability. Firstly, a calculation model of single-object vulnerability is built up by analyzing attributes of disaster-affected objects. Then the relationship between regional vulnerability and single-object vulnerability has been discussed and the comprehensive influence coefficient is introduced to measure the impact of natural environment and socioeconomic conditions. Based on these, the quantitative assessment model of regional vulnerability is established. We also present a case study to explain the application of this model.

Key words:disaster-affected objects; single-object vulnerability; regional vulnerability; model; comprehensive influence coefficient

doi:10.3969/j.issn.1000-811X.2016.02.040

中图分类号：X43；S166

文献标志码：A

文章编号：1000-811X(2016)02-0213-06

作者简介：姚思敏(1990-)，女，湖南衡阳人，硕士研究生，研究方向为暴雨灾害风险评估. E-mail: yaosimin01@163.com

基金项目：国家自然科学基金重大研究计划“灾害性气象事件影响预评估理论与方法研究”(91224004)

*收稿日期：2015-09-07修回日期：2015-11-05

姚思敏，钟少波，黄全义. 基于承灾载体单体脆弱性的区域脆弱性研究[J].灾害学, 2016,31(2):213-218.[ Yao Simin, Zhong Shaobo and Huang Quanyi. A Study on Regional Vulnerability Based on Single-object Vulnerability of Disaster-affected Objects[J].Journal of Catastrophology, 2016,31(2)：213-218.]