极端灾害天气下临河岩质边坡的倾覆稳定性分析*
2016-04-20师华鹏余宏明陈鹏宇
师华鹏,余宏明,陈鹏宇
(1.中国地质大学(武汉) 工程学院,湖北 武汉 430074;2.内江师范学院 地理与资源科学学院,四川 内江 641100)
极端灾害天气下临河岩质边坡的倾覆稳定性分析*
师华鹏1,余宏明1,陈鹏宇2
(1.中国地质大学(武汉) 工程学院,湖北 武汉 430074;2.内江师范学院 地理与资源科学学院,四川 内江 641100)
摘要:基于改进的水压分布假设,建立了临河岩质边坡在冻胀作用、静水压力和流水淘蚀等多因素影响下失稳的概化理论模型,并利用极限平衡理论推导出了极端天气下临河岩质边坡倾覆稳定性的无量纲表达式。重点分析了各影响因素对边坡倾覆稳定性的影响,绘制了饱水岩质边坡倾覆稳定性系数与坡高、坡角、临河水位以及水平淘蚀距离之间的关系图;同时分析了非饱水状态下边坡的倾覆稳定性系数与各影响因素的关系。算例分析表明:在极端天气的影响下,出溜缝未堵塞边坡的倾覆稳定性发生了很大的变化,其随着临河水位的升高先减小后增大,随淘蚀距离的增加而减低,随坡角、坡高的增加而增加,当坡高较低时,随冻深的增加而减低,当坡高较高时,随冻深的增加而增大。
关键词:临河岩质边坡,极限平衡法,倾覆稳定性,极端冰雪灾害,流水淘蚀
近年来,我国强降雨、冰雪等极端天气频繁出现,导致各地出现了严重的地质灾害。2008年1-2月,我国南方由于极端冰雪气候引发的地质灾害3 106 处,其中崩塌858处,占28%[1-2];2014年,强降雨造成了云南福贡、湖南安化和重庆云阳等地发生了大规模的滑坡灾害。极端天气引起的这些地质灾害发生的原因一是强降雨导致坡体地下水位上升,坡体呈过饱和状态,斜坡稳定性减低;二是由于水结冰的过程产生了体积膨胀导致坡体稳定性下降,产生滑坡和崩塌。因此,开展强降雨和冰雪等极端天气下边坡稳定性的研究对地质灾害防治有着现实指导意义。
目前,国内外学者对工程边坡稳定性多采用极限平衡法进行分析,取得了丰硕的研究成果。Hoek和Bray[3]详细分析了在地下水作用下的典型单滑面岩质边坡的抗滑稳定性,经过实例验证表明,饱水边坡比干燥边坡的滑动稳定性系数减少70%左右;谭龙金等[4]利用改进后的岩石边坡水力学分析模型,推导出边坡稳定性系数和决定边坡稳定性的张裂隙临界充水高度的表达式;夏开宗等[5]利用无量纲参数从不同角度对水力作用下顺层岩质边坡的稳定性进行了研究;罗伟等[6]在综合考虑了锚固效应、冻涨作用和地震荷载等因素下,推导出了典型岩质边坡的倾覆稳定性表达式;杨艳霞等[1]采用FLAC3D对处于饱和状态下的岩质边坡进行了数值模拟,并从冻胀深度和冻胀变形两个方面揭示了南方极端冰雪灾害下崩塌形成机理。以上就边坡的滑移破坏和典型边坡的冻胀破坏机理进行了系统研究,但均未涉及极端天气下临河岩质边坡的稳定性分析。基于此,本文利于改进的水压分布假设,推导出了极端天气下临河岩质边坡的一般倾覆稳定性表达式,并讨论了其随临河水位、河流淘蚀、坡高、坡角和冻深的变化规律。
1临河岩质边坡的抗倾覆稳定性分析
1.1计算模型及基本假设
本文提出的临河边坡稳定性的评价模型是建立在Hoek等[3]提出的典型不透水岩石边坡模型的基础上,如图1所示。其中坡体的几何要素包括以下几点:坡体高度H,临河水位Hr,坡脚淘蚀高度HA,裂隙深度Z,裂隙积水深度Zw,张裂隙距坡肩的距离B,坡脚距淘蚀壁面的距离Δx,坡面倾角β,坡趾淘蚀前边坡失稳角θ1,淘蚀后边坡失稳角θ2。由于θ2、B不是独立参数,根据几何关系可由下式求得:
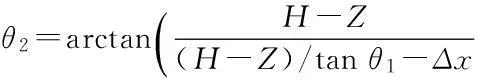
(1)
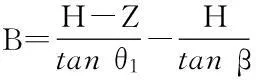
(2)
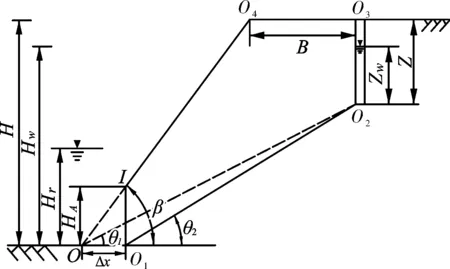
图1 典型临河岩质边坡的几何要素
临河天然岩质边坡并非如图1所示的那样规则,为便于计算,做出了如下假设:破坏面为一平面,其走向与坡面平行;张裂隙与坡趾淘饰面直立,走向与坡面平行,且在出流缝未堵塞时,水可沿张裂隙、滑面从坡脚进入大气;滑动面须在坡面出露,即θ1、θ2<β;裂隙内的冻涨力在冻深范围内均匀分布。
1.2临河岩质边坡的受力分析
本文为分析临河岩质边坡在极端天气下的倾覆稳定性时考虑了临河水位、淘蚀作用、冻胀作用以及出溜缝是否堵塞等因素的影响。当考虑冰雪冻胀作用时,将其等效为水平作用在冻深范围μZ(μ为冻结深度与张裂缝高度的比值,0≤μ≤1)内的均布荷载f[7-8];而对于静水压力,本文采用舒继森改进的水压分布假设来进行坡体内、外静水压力的计算[9],并假设出流缝未堵塞时,出流缝处滑面水压力与临河水压力相等,但出流缝左右总水头不一定相等,如图2所示。
以下分别计算坡体所受的各外力大小及其绕坡趾的力臂。
1.2.1滑体重力和地震作用力的计算
本文是在参考Hoek和Bray[3]提出的典型不透水岩质边坡模型的基础上,提出了临河岩质边坡的倾覆稳定性分析模型,因此本文假设坡体重度为天然重度,不考虑水对其重度的影响。由图1的几何关系知倾覆体自重W及质心G至坡趾O1的水平距离xG为:
(3)
(4)
1.2.2坡顶裂隙和滑面静水压力的计算
由上文的分析可知,坡体内所受静水压力的大小与出溜缝是否堵塞以及裂隙水位Zw有关。当出溜缝未堵塞且0≤Zw≤0.5Hw时张裂隙和滑面所受的静水压力P3,P4及其绕坡趾O1倾覆的力臂L3,L4分别为:
(5)
若0.5Hw≤Zw≤Hw,P3,P4和L3,L4分别为:
(6)
当出流缝堵塞时,静水压力P3,P4及其绕坡趾O1倾覆的力臂L3,L4分别为:
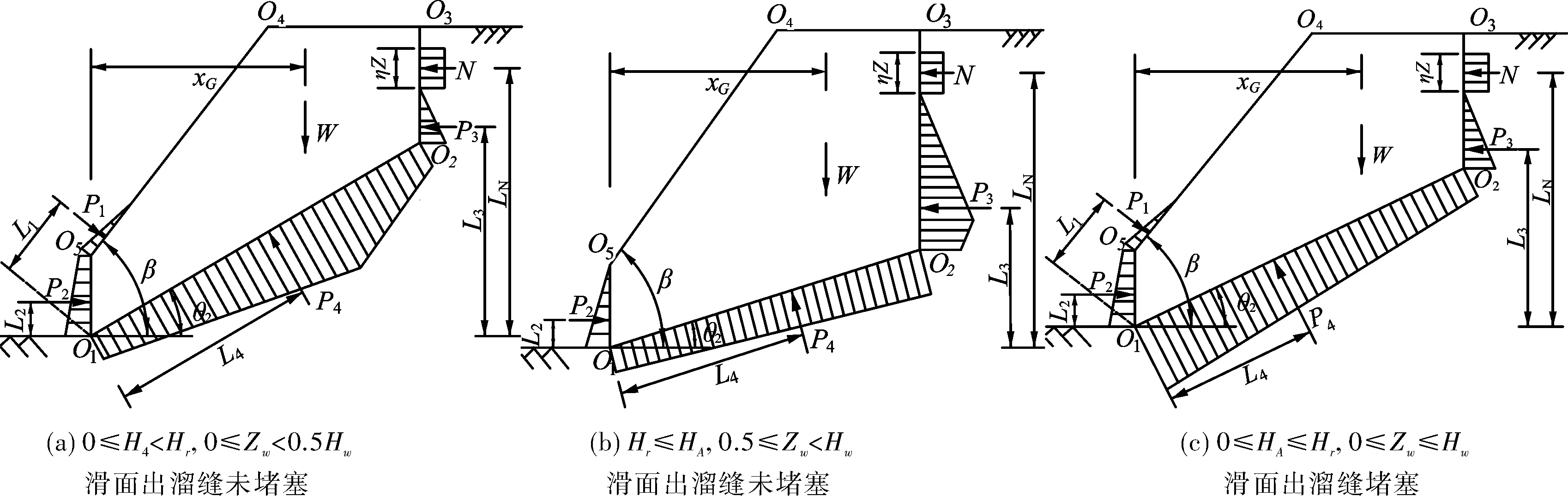
图2 典型临河岩质边坡的受力状态
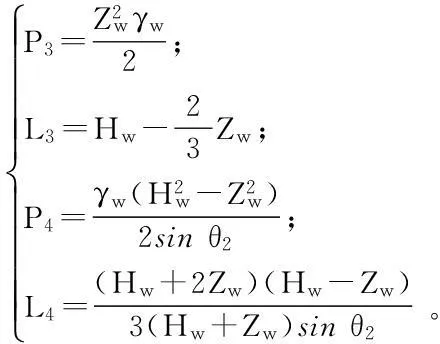
(7)
1.2.3临河静水压力的计算
对于临河水压而言,当0≤Hr≤HA时,静水压力P1,P2及其绕坡趾O1的抗倾覆力臂L2分别为:
(8)
当HA≤Hr时,P1,P2和L1,L2分别为:
(9)
1.2.4冻胀力的计算
在极端天气下,张裂隙内的冰对岩壁产生的侧向力N及其绕坡趾O1的倾覆力臂LN分别为:
(10)
1.3抗倾覆稳定系数求解
边坡最危险的倾覆破坏是绕坡趾的倾覆破坏[10]。根据边坡倾覆稳定性的定义,边坡的倾覆稳定性系数为绕坡趾的抗倾覆力矩Mresist与促倾覆力矩Minduce之比,即:
(11)
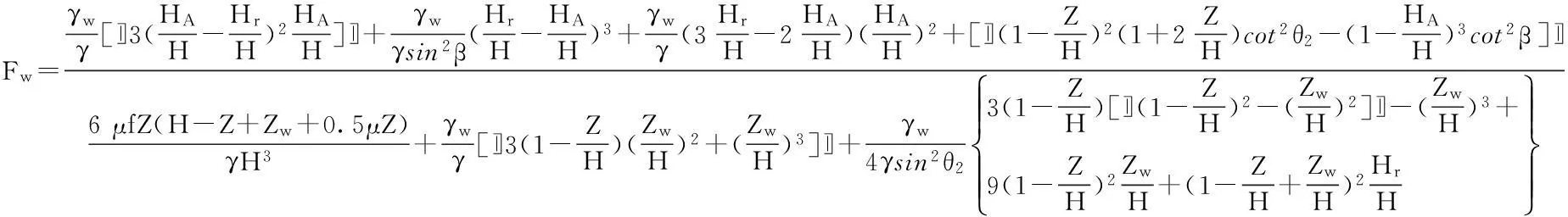
(12)
当0.5Hw≤Zw≤Hw(以HA≤ Hr为例),将式(3)、(4)、(6)、(9)和(10)代入到式(11)并将分子分母除以γH3/b,就得边坡倾覆稳定性系数Fw的无量纲表达式(13)。
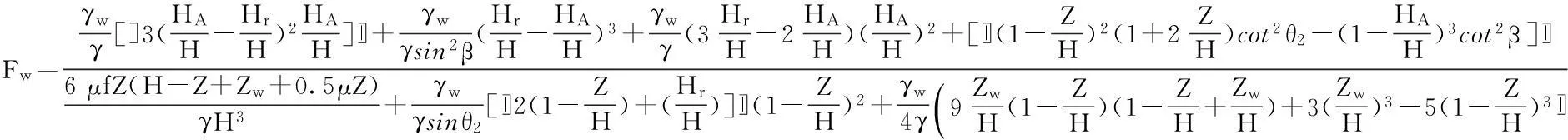
(13)
当滑面出溜缝堵塞时(以HA≤Hr为例),将式(3)、(4)、(7)、(9)和(10)得了边代入式(11)并将分子分母除以γH3/6,就坡倾覆稳定性系数Fw的无量纲表达式(14)。
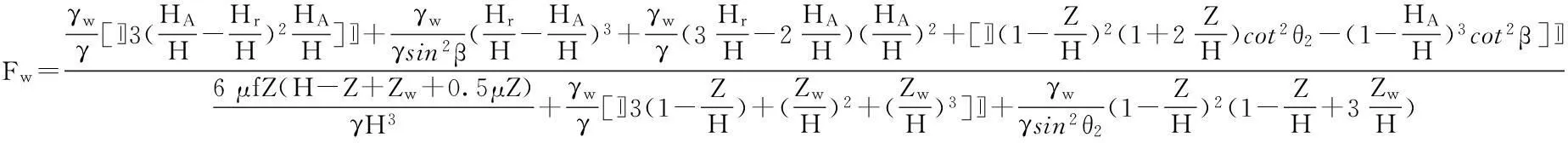
(14)
从式(12)、(13)、(14)可以看出无论临河岩质边坡滑面的出溜缝是否堵塞,后缘裂隙的水深与边坡倾覆稳定性都成反比,且裂隙水深Zw越大,倾覆稳定系数Fw就越小,边坡发生倾覆的可能性就越大。因此,在极端天气影响下,即后缘裂隙水位Zw=Z且发生冻胀作用时,边坡最有可能发生倾覆破坏,此时将Zw=Z-μZ代入式(12)、(13)和(14)就得到了极端天气下处于饱水状态的边坡倾覆稳定性系数Fw的计算表达式。但由于公式复杂,0≤Zw≤0.5Hw,HA≤Hr为例得到了Fw的表达式(15)。
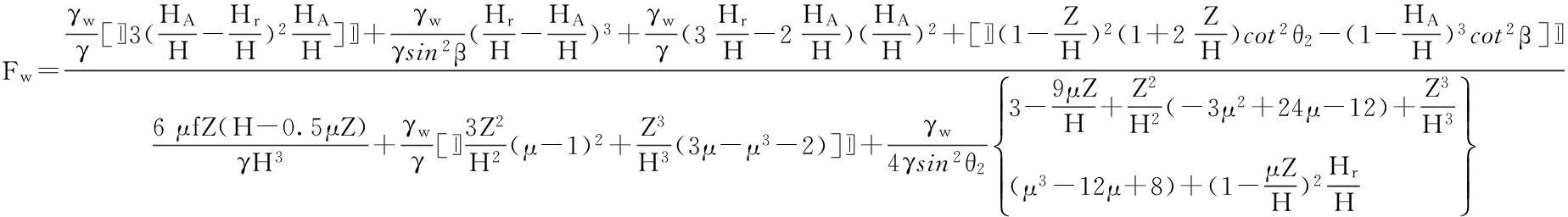
(15)
通过简单的初步计算发现饱水状态时的边坡受河水淘蚀作用、临河水位、冰雪冻胀作用以及坡体几何要素的影响显著。以下将以出溜缝未堵塞为例重点讨论临河边坡倾覆稳定性随它们变化的规律。
2影响饱水边坡倾覆稳定性的参数分析
为分析边坡倾覆稳定性在因素影响下的变化规律,现取临河边坡的基本参数为:H=10m,β=60°,Z=2,θ1=30°,γ=25kN/m3,γw=10kN/m3。
2.1水力赋存方式及淘蚀作用的影响
当Hr=2m,μ=0~1,Δx=0~3m,f=200kN/m时,根据Hoek提出的传统水压分布假设和改进的水压分布假设,分别求出了临河岩质边坡倾覆稳定性系数 ,其变化规律如图3所示。
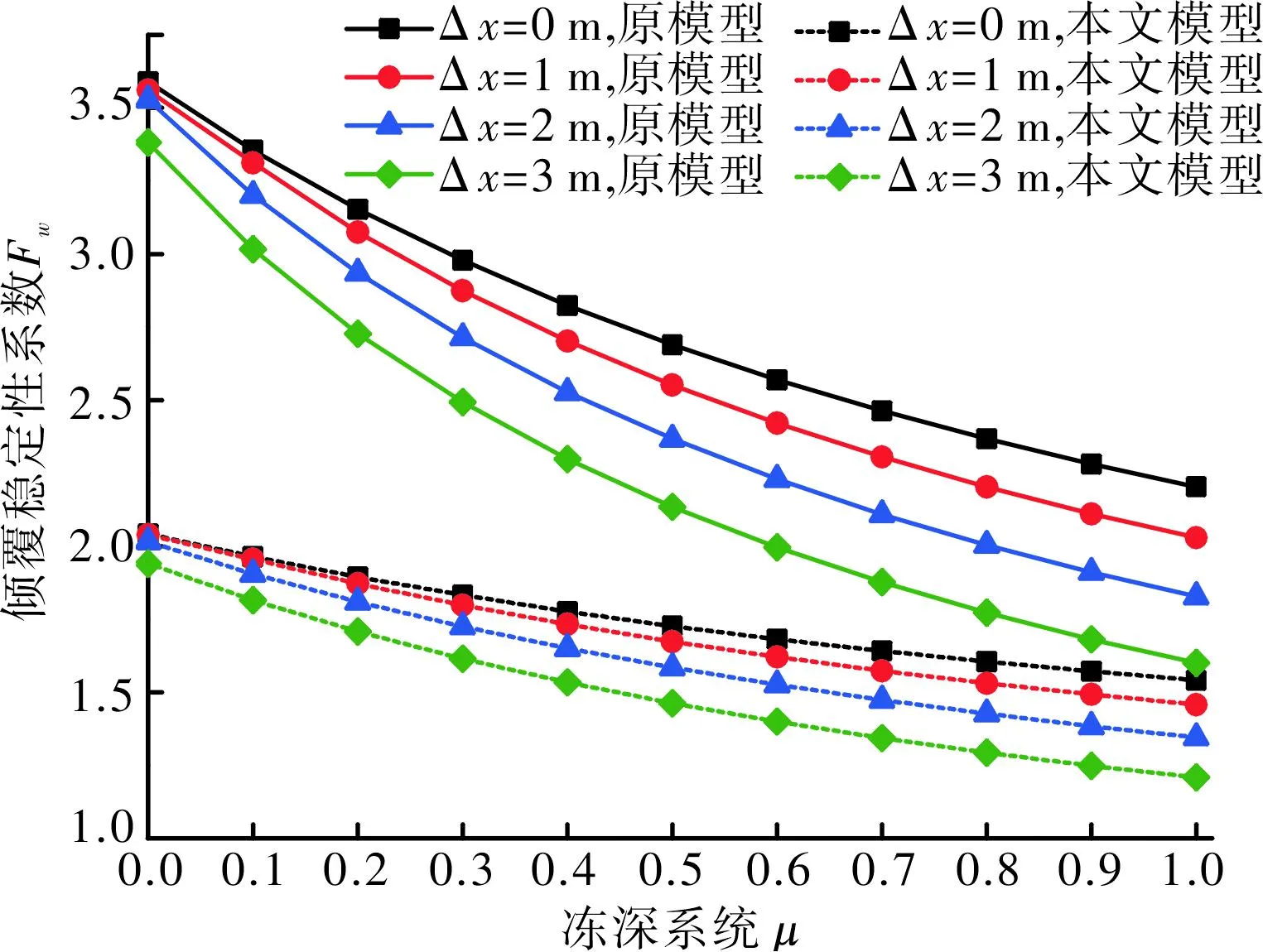
图3 不同的水力赋存方式下Δx与μ对Fw的影响
由图3可知:
(1)无论是采用传统的还是改进后的水压分布假设,当其他情况相同时,边坡倾覆稳定性系数Fw随着冻深的增加而明显下降。如当μ=0.5,Δx=0时,传统的和改进的水压分布假设下的边坡倾覆稳定性系数比未冻结时分别降低了25.1%、15.5%。这是由于随着冻深的增加,冻胀力引起的倾覆力矩的增加大于坡内静水作用引起的倾覆力矩的减少,导致了Fw的降低。
(2)相同条件下,Δx越大,临河边坡倾覆稳定性系数Fw就越小,且冻深对倾覆稳定性的影响程度就越明显。如在改进下的水压分布假设下,Δx分别取0m、1m、2m、3m,且μ=0.5时,Fw分别为1.727、1.674,1.585、1.463;与各自未冻结时Fw的比值分别为0.846、0.821、0.786、0.754,Fw的下降量随着Δx的增大而增大。
(3)在相同参数影响下,传统的水压分布假设计算得到的边坡倾覆稳定性比利用改进的水压分布假设计算得到的结果要大。如μ=0.3,Δx=0时,Fw分别为2.978、1.833。且由文献[9]中的式(2)知,当μ=1,Hw减小时,Fw是不变的,这与工程实际是不相符的。因此,在工程实际中运用改进的水压分布假设更为合理、安全。
2.2坡角对饱水边坡倾覆稳定性的影响
为讨论坡角对边坡倾覆稳定性的影响,取β=50°,Hr=2m,μ=0~1,f=200kN/m,Δx=0~3m。边坡倾覆稳定性Fw的变化规律如图4所示。
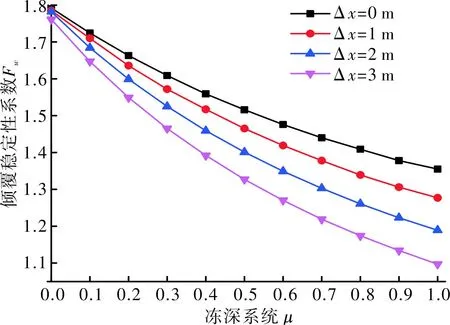
图4 坡角β=50°时Δx与μ对Fw的影响
由图4可知:
(1)结合图3可知,当其他参数相同时,边坡的坡角β越大,临河边坡的倾覆稳定性就越大。如μ=0.5,Δx=2m,β=50°时,Fw=1.401,但β=60°时,Fw=1.585。
(2)图3、图4都表明边坡倾覆稳定性系数Fw随着冻深的增加而明显下降,且Fw的下降速率越来越小。如Δx=2m,β=50°时,倾覆稳定性系数Fw在μ分别为0.2、0.4、0.6、0.8时的值与未冻结时Fw的比值分别为:0.897、0.819、0.757、0.708,其降低的速率越来越低。
(3)当冻深条件相同时,淘蚀作用Δx对倾覆稳定性的影响随着坡角的不同而不同,边坡越陡,淘蚀作用对边坡倾覆稳定性的影响程度就越明显。根据图3,图4分别取一组μ=0.8,坡角分别为50°、60°的边坡倾覆稳定性系数与边坡未受到冲刷作用时的比值来说问题,如表1所示。
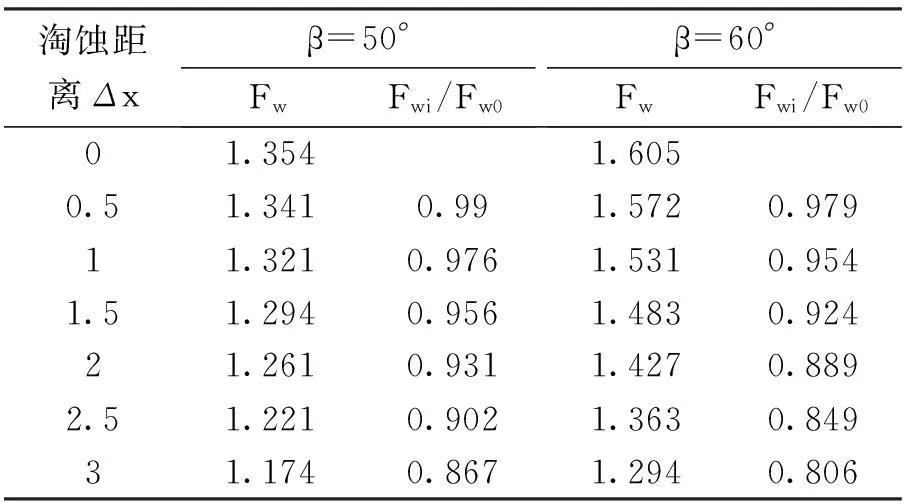
表1 μ为0.8时只考虑坡角变化的Fwi/Fw0变化表
2.3坡高对饱水边坡倾覆稳定性的影响
为分析坡高对稳定性的影响,现取坡高H=8、12、20、25、30m,β=60°,Z=2,θ1=30°,Hr=2m,μ=0~1,Δx=2m,f=200kN/m。边坡倾覆稳定性Fw的变化规律如图5所示。
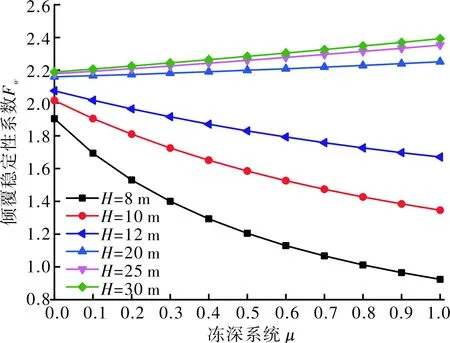
图5 不同坡高H下μ与Fw的关系
由图5可知:
(1)结合图3可知,在其他条件相同时,坡高越大,边坡的倾覆稳定性Fw就越大,且随着坡高的增加,Fw增加的速率越来越小;坡高越大,冻深对Fw的影响程度就越小,现取μ=0.8时的边坡倾覆稳定性系数Fw与未冻胀时的Fw0之比说明情况。如表2所示。
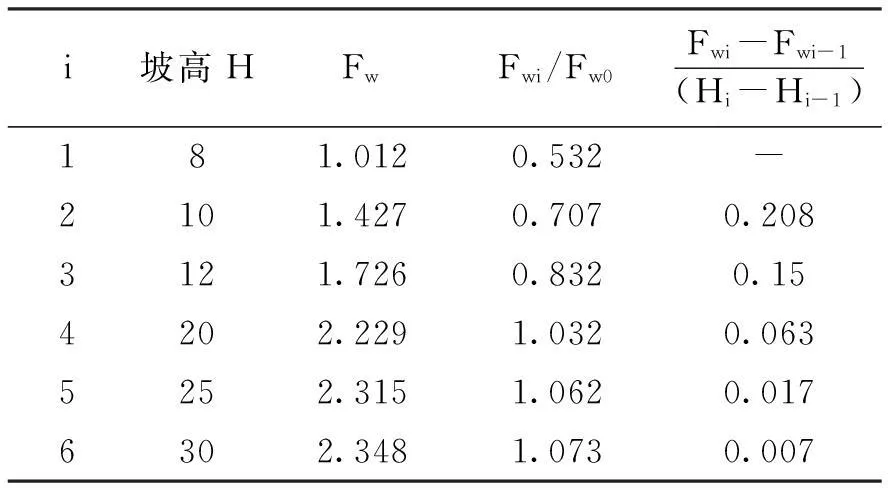
表2 μ为0.8时只考虑坡高变化的Fwi/Fw0变化表
(2)当坡高较低时,边坡倾覆稳定性系数Fw随着冻深的增加逐渐降低,原因如上文分析;而当坡高较高时,边坡倾覆稳定性系数Fw随着冻深的增加逐渐增大,这是由于随着μ的增加,冻胀力引起的倾覆力矩的增加小于坡内静水作用引起的倾覆力矩的减少,导致了Fw的升高。
2.4临河水位对饱水边坡倾覆稳定性的影响
为讨论临河水位变化时,临河边坡倾覆稳定性的变化规律,现取H=20m,β=60°,Z=2,θ1=30°,Hr=0~20m,Δx/H=0.2、0.4、0.6,μ=0.5,f=200kN/m。变化规律如图6所示。
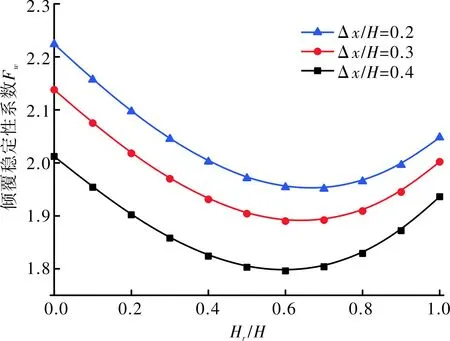
图6 不同淘蚀距离Δx下Hr与Fw的关系
由图6可知:
(1)边坡的倾覆稳定性随着临坡河流水位的增大,先减小后增大,表明了在较高水位(Hr/H≥0.65)下,河水位的上升有利于边坡倾覆稳定性的提高。这是由于Hr的增加导致了P1、P2对倾覆稳定性系数Fw的影响先小于后大于P3、P4对Fw影响的结果。
(2)再次验证了倾覆稳定性Fw随Δx的增加而降低;并且Fw随着Δx的增加,其减小的速率越来越快。结合图5,取Hr/H=0.1时,可得如表3的结果。

表3 Hr/H=0.1时Fw随Δx的变化表
3影响非饱水边坡倾覆稳定性的参数分析
根据公式(14)、(15)、(16)可知,当边坡后缘裂隙水位未达到裂隙高度且其他参数相同时,边坡的倾覆稳定性系数大于饱和状态时的倾覆稳定性系数,且裂隙水位越低,冻深越大,Fw就越大。
通过上述分析及公式的验算可知,临河水位、坡角、坡高和河水淘蚀作用对非饱水边坡倾覆稳定性的影响与对边坡处于饱和状态时的影响类似,变化规律相同,但由于篇幅限制,本文不再赘述。
4结论
本文在利用极限平衡理论的基础上,采取了改进的新水压分布假设,推到出了临河岩质边坡在流水淘蚀作用、临河水位、冰雪冻胀作用以及坡体几何要素等因素影响下的临河边坡倾覆稳定性系数表达式,并得到以下结论。
(1)裂隙冻胀力对饱水边坡倾覆稳定性的影响较为显著,使边坡的倾覆稳定性在不同情况下呈现有规律的变化:随水平淘蚀距离的增加而减低;随坡角、坡高的增加而增加;当坡高较低时,随冻深的增加而减低,当坡高较高时,随冻深的增加而增大。
(2)受季节性径流影响显著的山区临河边坡,应注意临河水位升降和河水淘蚀作用对边坡倾覆稳定性的影响。出溜缝阻塞的边坡临河水位较高时(Hr/H≥0.65),水位的骤涨有利于边坡倾覆稳定性的提高;但当水位较低时,水位的骤涨反而对边坡倾覆稳定性不利;同时,还需做好临河边坡坡趾的抗冲刷能力。
(3)对于非饱水岩质边坡,坡高、坡角、冻深、河水淘蚀作用对边坡倾覆稳定性的影响与处于饱水状态时的边坡相同,并且后缘水位越深,倾覆稳定性就越低,且公式对于不同的岩坡形式具有通用性。
参考文献:
[1]杨艳霞,祝艳波,李才,等. 南方极端冰雪灾害条件下边坡崩塌机理初步研究[J]. 人民长江,2012,43(2):46-49.
[2]韦方强,赵琳娜,江玉红,等. 2008年初南方雨雪冰冻灾害及其对山地灾害的影响[J]. 山地学报,2008,26(2):253-254.
[3]HoekE,BrayJW.RockSlopeEngineering[M]. 3rd.ed.London:InstitutionofMiningandMetallurgy, 1981.
[4]谭龙金,张海娜,盛韩微,等. 水力作用下缓倾顺层岩质边坡滑移破坏机制分析[J]. 长江科学院院报,2014,31(9):47-53.
[5]夏开宗,陈从新,鲁祖德,等. 考虑水力作用的顺层岩质边坡稳定性图解分析[J]. 岩土力学,2014, 35(10):2985-2995.
[6]罗伟,李亮,赵炼恒,等. 基于改进水压分布的岩石边坡倾覆稳定性分析[J]. 公路交通科技,2014,31(9):0030-0036.
[7]刘小宁,李庆祥. 我国最大冻土深度变化及初步解释[J]. 应用气象学报,2003,14(3): 299-308.
[8]中华人民共和国水利部.SL211-2006水工建筑物抗冰冻设计规范[S].北京:中国水利水电出版社,2006
[9]舒继森,王兴中,周毅勇. 岩石边坡中滑动面水压分布假设的改进[J]. 中国矿业大学学报,2004,33(5):509-512.
[10]许光祥. 饱水岩石边坡倾覆稳定系数计算[J].岩土工程学报,1999,21(2):227-229.
Overturning Stability Analysis of Rock Slope along River Under Extreme Disasters Weather
Shi Huapeng1, Yu Hongming1and Chen Pengyu2
(1.FacultyofEngineering,ChinaUniversityofGeosciences,Wuhan430074,China;2.CollegeofGeographyandResourceScience,NeijiangNormalUniversity,Neijiang641100,China)
Abstract:Based on the assumption of improved groundwater pressure distribution, a model of rock slope instability generalizability theory along river under the multiple factors of frost heaving, hydrostatic pressureand stream erosion at the slope is established, and the calculation formula of overturning stability factor of rock slope along river is derived by using limit equilibrium method. The model focuses on the influence of various factors on overturning stability of rock slope along river, and diagrams get drawn which express the relationship between slope height, slope angle, the water level, stream erosion distance and the coefficients of overturning stability when the rock slope is saturated; Thenthe relationship, between overturning stability of rock slope along river and various influence factor, is analyzed when the rock slope along river is unsaturated. The calculation example analysis shows that: the overturning stability of slope where outflow seam is unblocked has been greatly changed under the influence of extreme disasters weather, it decreases first, then increases as the water level along river rises; it decreases as the distance of eclipse increases; it increases as slope angle and height increases; when slope height keeps low, it decreases as frost depth increases, otherwise, it increases as frost depth increases.
Key words:rock slope along river; limit equilibrium method; overturning stability; extreme snow disaster; stream erosion
doi:10.3969/j.issn.1000-811X.2016.02.034
中图分类号:U416.1+4;X43
文献标志码:A
文章编号:1000-811X(2016)02-0176-06
作者简介:师华鹏(1988-),男,内蒙古乌拉特前旗人,硕士研究生,研究方向为岩土体的工程稳定性及地质灾害分析与防治.E-mail:276332792@qq.com通讯作者:余宏明(1952-),男,湖北咸宁人,教授,博士生导师,主要从事地质灾害分析与防治及岩土工程领域的教学与科研工作.E-mail:cugyhm@sina.com
基金项目:国家自然科学基金项目(41272377);国家自然科学基金青年基金项目(41302278)
*收稿日期:2015-08-05修回日期:2015-10-12
师华鹏,余宏明,陈鹏宇. 极端灾害天气下临河岩质边坡的倾覆稳定性分析[J].灾害学, 2016,31(2):176-181.[ Shi Huapeng, Yu Hongming, Chen Pengyu. Overturning Stability Analysis of Rock Slope along River Under Extreme Disasters Weather[J].Journal of Catastrophology, 2016,31(2):176-181.]
