鲁中主城区暴雨强度公式的修正方法

环海军，刘焕斌，刘　岩，夏福华

(1. 山东省淄博市气象局，山东　淄博　255048；2. 山东省气象局，山东　济南　250031)



鲁中主城区暴雨强度公式的修正方法

环海军1，刘焕斌2，刘岩1，夏福华1

(1. 山东省淄博市气象局，山东淄博255048；2. 山东省气象局，山东济南250031)

摘要：利用鲁中淄博地区1981～2013年降水资料，分析降水变化的时空规律。基于年最大值法选样，采用P-Ⅲ型分布、指数分布和耿贝尔分布对淄博主城区暴雨强度进行理论频率拟合分析，得出重现期—暴雨强度—历时的关系曲线，结合最小二乘法和高斯—牛顿法推求暴雨强度公式参数，以绝对误差和相对误差作为公式主要评价指标，得出淄博主城区暴雨强度公式。结果表明：淄博市近30 a来暴雨强度呈上升趋势，上升幅度由短历时向长历时递减；年平均暴雨日数呈现山区多、平原少的空间分布，其中，淄博主城区最少为1.6 d，南部山区博山最多为2.5 d；P-Ⅲ型分布曲线拟合理论频率—最小二乘法推求参数得到的暴雨强度总公式和单一公式效果最好，总公式平均绝对标准差和平均相对标准差分别为0.026 mm/min和2.35%；新修正的暴雨公式计算的暴雨强度值多数比1980年代编制的大，偏大幅度随重现期的增加而增加，对临近平原地区暴雨强度有较好的拟合效果。

关键词：变化规律；暴雨强度；分布曲线；参数；公式

引言

城市化的快速发展使得城市不断扩容、建筑密度加大，不透水路面增多，加上近年来，受全球气候变化影响，区域极端暴雨事件频发[1-5]，导致城市出现排水不畅和内涝现象。随着山东淄博主城区城镇化进程不断加快及城市规模不断扩大，在气候变化背景下，区域短历时强降水的强度和分布特征均发生了显著变化，极端降水事件强度增强，1988～2000年5 min平均暴雨强度是1.822 mm/min，而2001～2013年为2.328 mm/min，暴雨强度上升明显，加上老城区排水设施设计标准低、设施老化等原因，城区道路多处排水不畅，大面积的道路积水造成老城区交通严重堵塞、部分路段交通中断，修正暴雨强度公式迫在眉睫。

目前国内外对于暴雨强度公式已有许多相关方面研究，主要体现在3个方面：一是暴雨样本的选择方法；二是频率分布选用的模型；三是参数拟合的方法。张秉祥等[6-11]利用年多个样法、年超大值法和年最大值法推求暴雨强度公式，并进行不同取样法拟合效果的对比分析；Vivekanandan等[12-13]利用耿贝尔分布、正态分布、皮尔逊分布等分布曲线对数据进行频率拟合，并推求暴雨公式，进行拟合效果对比；张子贤等[14-21]利用高斯—牛顿法和最小二乘法等方法确定暴雨公式参数，并对推求的暴雨公式进行对比研究。

本文依据《室外排水设计规范》(GB50014-2006，2014年版)、《城市暴雨强度公式编制和设计暴雨雨型确定技术导则》等技术规范和导则，利用年最大值选样法选样，利用P-Ⅲ型分布、指数分布和耿贝尔分布3种频率分布曲线进行暴雨强度理论频率拟合，结合最小二乘法和高斯—牛顿法推求暴雨公式参数，最终得出暴雨强度公式，并从拟合效果与精度的角度对公式进行比较，选择适合淄博主城区应用的暴雨强度公式和修订方法。

1资料与方法

1.1资料

资料来源于淄博市主城区1981年1月至2013年12月共计33 a的自记雨量记录原始数据，降雨历时选取5 min、10 min、15 min、20 min、30 min、45 min、60 min、90 min、120 min、150 min和180 min共11个历时，每年每个历时选取一个最大雨量记录数据，各时段最大降水量从年报表降水量部分获取(缺少资料从降水自记纸读取，不受日、月界的限制，但不跨年挑取)，将获得的各年最大降水量除以降水历时得到各年各历时的降水强度，将各历时的降水强度按照降序排列，得到不同历时降水强度序列，用于经验频率拟合。

1.2方法

(1) 暴雨强度公式

目前各国采用的暴雨强度公式不同[21]，国内主要依据《室外排水设计规范》(GB50014-2006，2014年版)，暴雨强度公式定义为：

(1)

式(1)中：q为暴雨强度(单位：L/(s·hm2)，P为重现期(单位：a)，指相等或超过它的暴雨强度出现一次的平均时间，取值范围为2～100 a；t为降雨历时(单位：min)，取值范围为1～180 min。重现期越长、历时越短，暴雨强度就越大，而A1、b、C、n是与地方暴雨特性有关且需要求解的参数：A1为雨力参数，即重现期为1 a时的1 min设计降雨量(单位：mm)；C为雨力变动参数；b为降雨历时修正参数，即对暴雨强度公式两边求对数后能使曲线化成直线所加的一个时间参数(单位：min)；n为暴雨衰减指数，与重现期有关。

固定重现期P，令A=A1(1+ClgP)，则暴雨强度单一公式为：

(2)

(2)暴雨强度公式的拟合方法

利用P-Ⅲ型分布、指数分布和耿贝尔分布3种频率曲线确定重现期—暴雨强度—历时(P-q-t)对应数值。暴雨强度重现期P为暴雨强度频率P1的倒数，计算公式见(3)式，其中N为样本总数(N=资料年限长度)，M为样本的序号(样本按从大到小排序)，文中的经验频率为不同频率上的暴雨强度。

(3)

(4)

(5)

(6)

由公式(4)、(5)、(6)拟合出P-q-t关系值，利用公式(1)，结合最小二乘法和高斯—牛顿法推求参数(A1，C,b，n)(公式略)，最终得出暴雨强度公式及相关曲线。

(3)精度检验

为确保计算结果的准确性，对暴雨强度计算结果进行精度检验，计算出重现期2～20 a的暴雨强度，并将算得的暴雨强度理论值与实测值的平均绝对均方误差和平均相对均方误差，与《室外排水设计规范》(GB50014-2006，2014年版)规定的精度对照。规范规定：计算重现期在2～20 a时，在一般强度的地方，平均绝对方差不宜>0.05 mm/min。在较大强度的地方，平均相对方差不宜>5%。平均绝对均方误差与平均相对均方误差计算公式如下：

(7)

(8)

式中，R′为理论降水量，利用修正的暴雨公式计算的暴雨强度(q)乘以历时得到的降水量；R为实际降水量，由3种频率曲线确定的P-q-t关系值中的暴雨强度(q)乘以历时得到的降水量。

2结果与分析

2.1暴雨强度变化

2.1.1时间变化

近30 a来，淄博主城区暴雨强度随时间的变化见图1。从年际变化(图1a)来看，暴雨强度呈明显增加趋势，尤其是短历时暴雨，增加幅度随历时增长而变缓，说明短历时强降水强度越来越大。从年代际变化(图1b)来看，2000年代部分历时有小幅度的下降，但短历时暴雨2010年后明显上升，整体来看暴雨强度仍呈上升趋势，短历时暴雨强度上升最为明显，这对城市排水及相关设计要求越来越高，故重新修订暴雨强度公式以符合实际降水变化。

图1　暴雨强度的年际(a)与年代际(b)变化

2.1.2空间变化

利用1981～2013年淄博市各区县暴雨日数年平均值绘制淄博市暴雨日数空间分布图(图2)。可以看出淄博市南部山区暴雨日数偏多，平均为2.3 d，北部平原偏少，平均为1.7 d，暴雨日数呈现出四周多、中间少的分布规律。

图2　淄博市年平均暴雨日数空间分布(单位：d)

由上述分析可知，不同地区应修订不同的暴雨强度公式，尤其是暴雨强度差异较大的山区和平原，故本文研究的暴雨强度公式只适用于淄博市主城区以及临近平原地区，山区应运用当地降水资料结合本文中的方法进行暴雨公式修订研究。

2.2暴雨强度频率曲线拟合

对11个历时的年最大值法统计的暴雨强度样本进行P-Ⅲ型分布、耿贝尔分布、指数分布理论频率拟合，并用最小二乘法对参数进行估计，求出3种分布曲线对11个降水历时暴雨强度频率拟合分布参数(表1)。利用表1中参数得到暴雨强度频率分布函数，求出各重现期对应的暴雨强度，制作反映暴雨重现期—强度—历时(P-q-t)三者关系(表2)。

2.3暴雨强度总公式参数拟合及精度检验

2.3.1暴雨强度总公式

利用表2中的P-q-t值，结合最小二乘法和高斯—牛顿法分别推求暴雨强度总公式的相关参数(表3)。将不同方法求得的雨力参数A1、雨力变动参数C、降雨历时修正参数b、暴雨衰减指数n代入公式(1)可得不同的暴雨强度总公式。

表1　暴雨强度频率3种分布曲线参数

表2　暴雨强度频率3种分布曲线P-q-t关系表

注：表中暴雨强度q单位为：mm/min

表3　不同方法推算的暴雨强度总公式参数

2.3.2暴雨强度总公式精度检验

利用重现期2～20 a的暴雨强度计算的平均绝对均方误差和平均相对均方误差对总公式及单一公式进行检验，误差分析见表4。利用P-Ⅲ型分布拟合P-q-t值和最小二乘法推算参数的暴雨强度总公式和单一公式误差最小，平均绝对均方误差分别为0.026 mm/min、0.016 mm/min，其次是P-Ⅲ型分布—高斯牛顿法、耿贝尔分布—最小二乘法和指数分布—高斯牛顿法推算的暴雨强度公式，均符合《室外排水设计规范》(GB50014-2006，2014年版)的精度要求，而指数分布—最小二乘法推算出的总公式精度不满足规范要求。

表4　不同方法暴雨强度公式误差分析

2.4理论值及旧公式的对比

2.4.1与理论值的比较

将精度<0.4的总公式计算的暴雨强度与理论值进行对比(图3)。可以看出4个暴雨强度公式计算的暴雨强度均比较接近理论的P-q-t值，有很好的拟合效果，其中以P-Ⅲ型分布—最小二乘法拟合的公式效果最好。

2.4.2与旧公式的比较

淄博市现行的旧暴雨强度公式(9)为1980年代初由淄博市设计院利用年多个样法编制的。通过上述拟合效果及精度分析，用P-Ⅲ型分布—最小二乘法拟合的公式(10)效果最好。

(9)

(10)

(11)

图3　不同暴雨强度公式计算的暴雨强度值与理论值的对比

利用暴雨强度距平百分率比较分析新暴雨强度公式与旧暴雨强度公式计算的暴雨强度值，计算方法为公式(11)，式中，Eq为暴雨强度距平百分率，q1、q0分别为新公式、旧公式计算的暴雨强度值(mm/min)，分析结果见图4，可以看出新公式计算的暴雨强度值大多数比旧公式偏大。随着重现期的增加，新旧公式计算的暴雨强度距平百分率逐渐增大，100 a重现期各历时平均距平百分率为3.55%。

2.4.3对其他临近地区的适用性分析

将新修正的暴雨公式用于推求临近平原地区高青县的暴雨强度，并与高青国家一般气象站1980～2011年实测暴雨经验频率在频率格纸图上进行对比(图5)，可见由主城区暴雨强度公式计算得到的高青县的暴雨强度频率基本与实测频率一致，低频率(长重现期)的计算值与实测值十分接近，高频率(短重现期)的计算值较实测值略偏大。短历时的暴雨强度计算值与实测值接近，随着历时的增长，计算值与实测值差值有所增大，新修正的主城区暴雨公式在短历时长重现期(暴雨强度较大)计算临近平原地区的暴雨强度效果较好。故新修正的暴雨公式能够用于推求临近平原地区不同重现期不同历时的降水强度，从而适用于城市排水设计和防灾减灾等方面。

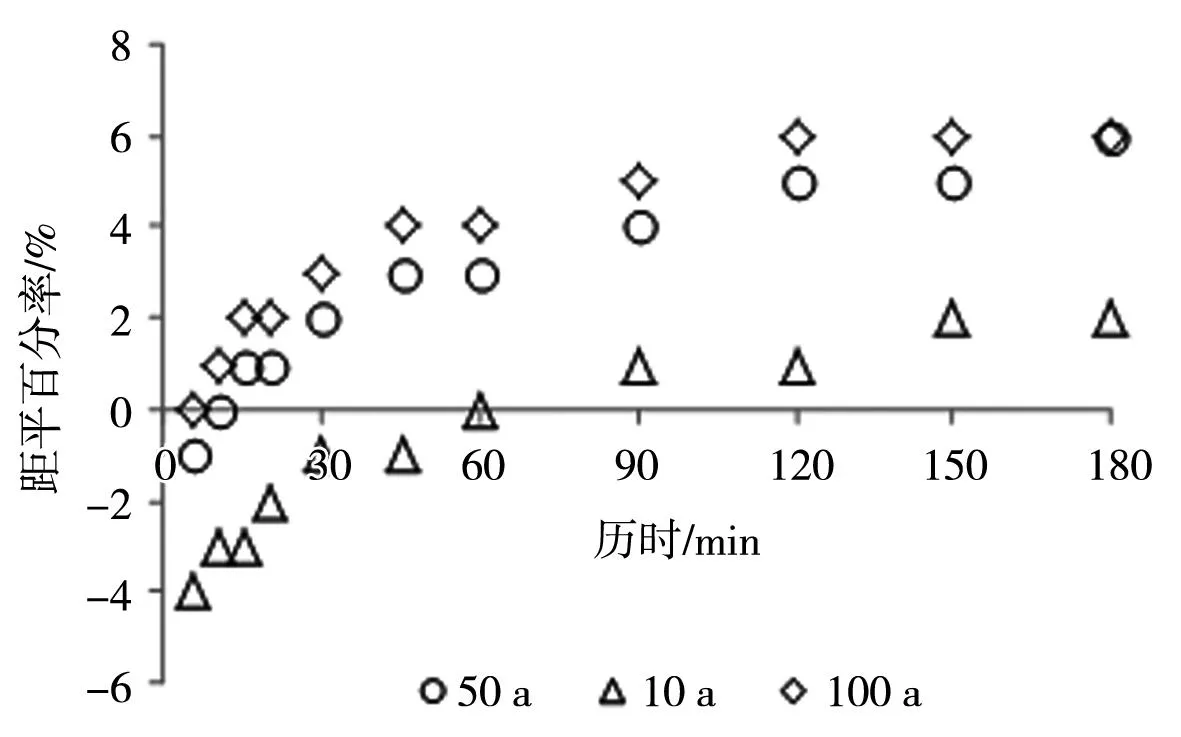
图4　新旧暴雨强度公式拟合的

图5　高青实测暴雨强度经验频率与公式计算值的对比

3结论

(1)淄博市近30 a暴雨强度有增加趋势，暴雨日数呈现山区偏多、平原偏少的空间分布，不同地区应定期分别结合降水资料对当地的暴雨强度公式进行修订，以符合当地的降水变化特征。

(2)通过年最大值法选样，采用P-Ⅲ型分布、指数分布和耿贝尔分布对暴雨强度进行理论频率拟合分析，结合最小二乘法和高斯—牛顿法推求暴雨强度公式参数，以绝对误差、相对误差和拟合效果作为公式评价指标，得出通过P-Ⅲ型分布曲线拟合理论频率—最小二乘法推求参数得到的暴雨强度总公式和单一公式效果最好，总公式平均绝对标准差和平均相对标准差分别为0.026 mm/min和2.35%，满足相关规范精度要求。

(3)新修正的暴雨公式计算的暴雨强度值大多数比修订前的公式偏大，偏大幅度随重现期的增加而增加。新旧暴雨强度公式选样方法不同，比较分析仅作为参考，随着降水资料序列的延长，年最大值法更利于暴雨公式的修订和符合暴雨强度的演变规律。

(4)新修正的主城区暴雨公式推求临近平原地区不同重现期不同历时的降水强度与实测值基本一致，对短历时长重现期计算效果较好，能够用于临近地区暴雨强度的计算。

(5)随着气候不断变化，暴雨强度的时空变化规律也在变化，因此，随着降水资料序列的延长以及城市规模的变化，对暴雨强度公式进行及时修订是十分必要的。

参考文献:

[1] 张爱英,高霞,任国玉. 华北中部近45 a极端降水事件变化特征[J]. 干旱气象，2008，26(4):46-50.

[2] 陈波,史瑞琴,陈正洪. 近45年华中地区不同级别强降水事件变化趋势[J]. 应用气象学报，2010，21(1):47-54.

[3] 高理，胡桂芳，孙莎莎. 山东夏季强降水的时空演变特征及成因[J]. 干旱气象，2013，31(4):690-694.

[4] 朱义青,胡顺起,张品竹,等. 山东南部一次大暴雨过程的中尺度特征及成因分析[J]. 干旱气象,2015,33(1):119-127.

[5] 万明波,董旭光. 山东省1961～2010年降水的非均匀性特征[J]. 干旱气象,2015,33(4):566-573.

[6] 张秉祥，陈静，韩军彩，等. 石家庄市城区暴雨强度公式修正方法对比分析[J]. 干旱气象，2014，32(4):671-676.

[7] 黄津辉，向文艳，户超，等. 天津市设计暴雨方法比较及公式修正[J]. 天津大学学报，2013，46(4):354-360.

[8] 卢金锁，程云，郑琴，等. 西安市暴雨强度公式的推求研究[J]. 中国给水排水，2010，26(17):82-84.

[9] 任伯帜，许仁荣. 基于Marqardt Hartley法及其在求解城市暴雨强度公式参数中的应用研究[J]. 湖南大学学报(自然科学版)，2002，29(3):96-100.

[10] 邓培德，韦鹤平，俞庭康，等. 城市暴雨公式统计方法的研究[J]. 同济大学学报，1985(1):26-30.

[11] 邵尧明. 最大值选样配合指数分布曲线推求雨强公式[J]. 中国给水排水，2003，19(13):142-144.

[12] Vivekanandan N．Analysis of hourly rainfall data for the developmentof IDF relationships using the order statistics approachof probability distributions[J]. International Journal of Management Science and Engineering Management，2013，8(4):283-291.

[13] Arelt A. Modelling of Short Duration Rainfall IDF Equationfor Bangalore City[J]. Research & Reviews: Journal of Engineeringand Technology，2013，2(3):80-86.

[14] 张子贤. 用高斯—牛顿法确定暴雨公式参数[J]. 河海大学学报，1995，23(5):106-111.

[15] 顾骏强，陈海燕，徐集云. 瑞安市暴雨强度概率分布公式参数估计研究[J]. 应用气象学报，2000，11(3):355-363.

[16] 孔祥瑞，陈淑芬，李梅，等. 济南短历时暴雨强度公式研究[J]. 山东建筑大学学报，2013，28(5):445-448.

[17] 李树平，刘遂庆，黄廷林. 用麦夸尔特法推求暴雨强度公式参数[J]. 给水排水，1999，25(2):26-28.

[18] 任伯帜，沈良峰，许仕荣，等. 带因子—迭代法求解城市暴雨强度公式[J]. 中国给水排水，2002，18(2):63-65.

[19] 邹长武，熊建秋，李柞泳. 改进的蚂蚁算法及其在暴雨强度公式参数优化中的应用[J]. 四川大学学报，2005，37(5):9-13.

[20] 程健，金菊良，张礼兵. 加速并行遗传算法及其在暴雨强度公式参数优化中的应用[J]. 安全与环境学报，2006，6(3):18-20.

[21] 付峥嵘,庄佳欣,杨琳芳. 谈暴雨强度公式研究现状的几点看法[J]. 山西建筑，2014,40(26)：130-131.

Revising Method of Rainstorm Intensity Formula in Main Urban in Middle Area of Shandong Province

HUAN Haijun1，LIU Huanbin2, LIU Yan1, XIA Fuhua1

(1.ZiboMeteorologicalBureauofShandongProvince,Zibo255048,China;2.ShandongProvincialMeteorologicalBureau,Ji’nan250031,China)

Abstract:Based on precipitation data from 1981 to 2013 of Zibo in the middle area of Shandong Province, the temporal and spatial variations of precipitation were analyzed firstly. According to the annual maximum value sampling method, combined with P-Ⅲ distribution, exponential distribution and Gumbel distribution, the theoretical frequency of rainstorm intensity in main urban area of Zibo was simulated and analyzed, at the same time, the relationship curve of return period, rainstorm intensity and rainfall duration was given, then on the basis of the least square method and Gauss-Newton method, the parameters of rainstorm intensity formula were calculated. Finally, using absolute error and relative error as the main evaluation indexes of the formula, the rainstorm intensity formula was obtained for the main urban area of Zibo. The results show that rainstorm intensity in Zibo in recent 30 years showed an upward trend, and rising amplitude decreased from short duration to long duration. The average annual rainstorm days in the plain were more than that in the mountain areas.The single and general formulas obtained by P-Ⅲ distribution and the least square method were the best, and the average absolute standard deviation and relative standard deviation of total formula were 0.026 mm/min and 2.35%, respectively.The values of rainstorm intensity caculated by new formulas were more than those caculated by the old rainstorm intensity formulas worked out in the 1980s, and increasing amplitude increased with the return period. The revising rainstorm intensity formulas had good fitting effect on rainstorm intensity in adjacent plain areas.

Key words:regularity；rainstorm intensity；distribution curve；parameters；formula

中图分类号：P457.6

文献标识码：A

文章编号：1006-7639(2016)-01-0188-07

doi:10.11755/j.issn.1006-7639(2016)-01-0188

作者简介：环海军(1987-)，男，汉族，江苏南通人，研究生，工程师，研究方向为农业气象.E-mail:324380521@qq.com通讯作者：刘焕斌，E-mail:hb_liu@126.com

基金项目：山东省气象局气象科学科技研究项目(2014sdqxm03)资助

收稿日期：2015-09-23；改回日期：2015-12-31

环海军，刘焕斌，刘岩，等.鲁中主城区暴雨强度公式的修正方法[J].干旱气象，2016，34(1)：188-194, [HUAN Haijun，LIU Huanbin, LIU Yan, et al. Revising Method of Rainstorm Intensity Formula in Main Urban in Middle Area of Shandong Province[J]. Journal of Arid Meteorology, 2016, 34(1):188-194], doi:10.11755/j.issn.1006-7639(2016)-01-0188