WRF模式中地形重力波参数化方案应用及不同拖曳力试验

艾　凯，郑益群,2，陈浩伟

(1. 解放军理工大学气象海洋学院，江苏　南京　211101； 2. 江苏省气候变化协同中心，江苏　南京　210093)



WRF模式中地形重力波参数化方案应用及不同拖曳力试验

艾凯1，郑益群1,2，陈浩伟1

(1. 解放军理工大学气象海洋学院，江苏南京211101； 2. 江苏省气候变化协同中心，江苏南京210093)

摘要：在WRF模式中引入地形重力波拖曳参数化方案(GWDO),利用WRFV3.2中尺度模式对2007年7月3日00时至10日00时(世界时)发生在我国江淮梅雨季向华北雨季转换时段江淮与华北地区过渡区域的降水天气过程进行了不同重力波拖曳力作用下的敏感性试验，设计了5组数值试验：不考虑重力波拖曳的控制试验(Ctrl)及考虑重力波拖曳(GWDO)但在不同拖曳力作用下的4组敏感性试验。结果表明：GWDO方案的引入，有效地改善了模式对环流场、水汽输送带、垂直速度场的模拟，缓解了对风速预报偏强的现象，一定程度上纠正了模式模拟的西风偏差，对降水落区和强度也有较好的改善。随着模拟时次的推移，引入的拖曳力越强，对降水模拟的改善越显著。

关键词：地形;GWDO参数化方案;数值模拟

引言

我国幅员辽阔、地形复杂，地形对我国天气和气候乃至东亚的大气环流都有显著影响。数值模式中引入地形的作用能够有效改进预报的准确性，也能很好地延长预报时长。次网格地形的参数化是研究地形作用的主要方法。目前，对地形参数化的方法主要有2种，一种是Wallace等[1]和Tibaldi[2]提出的“包络地形”方案，考虑了次网格尺度地形标准偏差倍数的虚假地形，可以改善模式的地形结构，弥补模式对总山脉拖曳的过低估计；另一种是地形重力波拖曳方案。由地形激发出的重力波波动能把相当大的水平动量传输到波动被吸收或耗散的区域，这种波动通量的耗散称为地形重力波拖曳力。当气流越过不规则的下垫面，起伏不平的地形可能会激发起向上传播的地形重力波，这种波动在传播过程中在某一特定层被反射或吸收，或是遇到对流不稳定的层结，重力波会受到破坏并崩溃[3]。重力波拖曳作用不仅能影响高层风场，还能进一步影响云和降水。由于地形重力波波长太小，在一般的模式中很难进行合理的数学处理，所以只能采用参数化方案代表由地形引起的重力波在垂直方向的传播，以及其对天气系统的影响。中尺度WRF模式在WRF3.1版本引入了地形重力波拖曳(GWDO)参数化方案，实验表明该参数化方案的引入能够有效缓解因大尺度数值模式不能精确分辨次网格地形而造成的“西风偏差(Westerly bias)”和“冷极(Cold pole)”问题[4-8]。许多学者就地形重力波做了大量工作并得到一些有益的结论，如乌元康[6]系统地解释了地形重力波拖曳的参数化；覃卫坚等[9]研究发现惯性重力波的传播与风速垂直切变有关，并随风速垂直切变的增大而增强，急流成为惯性重力波最重要的波源，急流下方是最易激发重力波的地方；王文等[10]运用地形重力波方案对暴雨天气模拟，认为只有同时考虑重力波和对流运动的相互作用，才能较完整地解释雨带的强度和特征得以发展和维持的原因；刘蕾等[11-12]利用地形重力波参数方案对华南地区的暴雨发生机制进行研究，发现地形重力波参数方案能很好地模拟暴雨的中心位置和强度，重力波能使垂直上升运动加强；王莉[13]通过GWDO参数化方案以及地形对大别山暴雨的影响研究指出，GWDO参数化方案的引入，能够有效改善复杂地形特别是山区地形的降雨，使模式能更好地再现实况的发生背景；刘佳等[14]对一次暴雨过程的重力波特征分析中发现重力波与暴雨有一定的内在联系，重力波引导了暴雨的发展；徐国强等[15]发现GRAPES模式中引进地形重力波过程，可以延长GRAPES模式的可用预报时效，提高全球形势预报的准确率，改善大气流场的分布，使预报流场更接近大气的真实状态，从而提高降水预报的准确率。上述研究表明在模式中引入地形重力波对模拟效果的改进有很好的效果，但对引入的拖曳力大小及合理性研究比较缺乏。

本文将利用WRF3.2模式，对2007年7月3日00时至10日00时(世界时,下同)发生在我国江淮梅雨季向华北雨季转换时段江淮与华北地区过渡区域的降水天气过程进行不同重力波拖曳力作用下的敏感性试验，通过对环流场和降水影响的分析，探究区域复杂地形的重力波拖曳处理技术方案。

1模式和试验方案

1.1数值模式简介

WRF(Weather Research Forecast)模式是1997年由美国国家大气研究中心(National Center for Atmospheric Research，NCAR)、美国国家大气海洋局(National Oceanic and Atmospheric Administration，NOAA)、美国国家环境预报中心(National Centers for Environmental Prediction，NCEP)、美国地球系统研究实验室(Earth System Research Laboratory，ESRL)、美国空军气象局(Department of Defense’s Air Force Weather Agency，AFWA)、美国海军研究实验室(Naval Research Laboratory，NRL)和美国俄克拉荷马州立大学的风暴分析和预报中心(Center for Analysis and Prediction of Storms，CAPS)等多家科研机构共同研发的新一代中尺度预报模式(next-generation mesoscale forecast model)，现已广泛应用于各种研究与业务预报中。2009年发布的WRF3.1版本引入地形重力波拖曳方案(GWDO)并应用到之后的版本中，来处理区域复杂地形非静力模式的重力波拖曳技术。

1.2地形重力波拖曳参数化方案(GWDO)简介

重力波是因稳定大气受到扰动而产生的惯性震荡的传播，当地形足够大时，基本气流相对缓慢，稳定的层结越过山脉时，会激发出地形重力波，在合适的条件下，这种重力波会向上或者上游传播。

次网格地形激发的重力波拖曳(Orographic Gravity Wave Drag,GWDO)作用不仅能影响高层的风场，还能进一步影响云和降水，对维持大气环流的动量、能量守恒过程具有非常重要的作用[16]。现有模式对下垫面的一些特征及复杂地形不能通过数学方程或概念模型很好地描述，且次网格地形激发的地形重力波波长较小，水平尺度在数公里至几百公里之间，维持数小时，在物理方程中次网格过程几乎被忽略，大多数数值模式中都不能用数学方程来计算处理，模式采用一个简单的参数化方案来表示地形重力波，即地形重力波拖曳参数化方案。GWDO参数化方案主要利用“平均地形”[17]，即在模式格点区域上采用平均高分辨率地形资料的方法，类似地形可直接在模式中通过可分辨动力学来处理完成对GWDO参数化。

GWDO参数化方案已在多个业务、科研模式中得到广泛应用，如ECMWF全球模式、NCEP全球模式和WRF模式等。本工作则通过WRF模式phys模块下module_bl_gwdo.F子程序对地形重力波及强度进行调试控制。

1.3试验设计

利用WRF3.2版本共设计了5组数值试验：不考虑重力波拖曳的控制试验(Ctrl)，考虑重力波拖曳(GWDO)但在不同拖曳力系数下的4组敏感性试验。如表1所示，次网格地形阈值为次网格山体规模大小的调谐参数，其值越大所产生的拖曳波越弱，次网格地形阈值越大相对应的拖曳力系数越小，其默认值为50 km，同时选取模式水平分辨率为12 km、36 km以及100 km进行试验，其中阈值越大(小)表示产生的重力波拖曳效果越弱(强)。5组试验均采用YSU边界层方案、Grell-Freitas ensemble积云参数化方案、Noah陆面过程、RRTM长波辐射方案和Dudhia短波辐射方案。采用两重嵌套网格，水平分辨率为36 km、12 km，试验区域中心经纬度为(30°N，115°E)，水平格点数分别为D1(150×140)、D2(271×250)，垂直方向为28层，模式层顶为50 hPa。模式初始场和侧边界均采用NCEP gfs一日4次分析场数据，侧边界场每6 h更新一次。起报时间为2007年7月3日00时(世界时)，进行为期一周的预报。为了探究引入次网格地形对模拟结果的影响，重点对第1重区域粗网格的模拟结果进行分析，区域平均也是针对第1重区域36 km的网格进行的。图1给出模拟区域的地形高度，从东到西三级阶梯分明。

表1　地形重力波拖曳参数化方案设计

注：其中阈值越大(小)表示产生的重力波拖曳效果越弱(强)

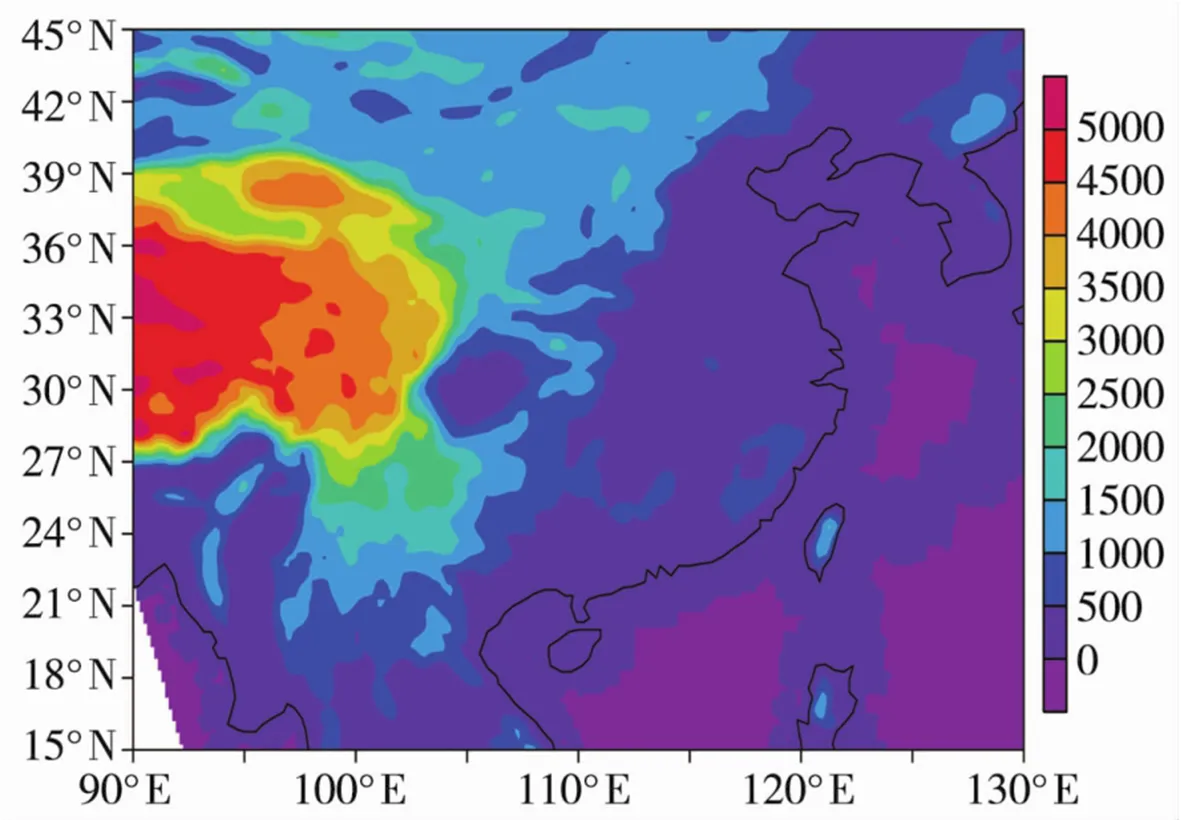
图1　模拟区域的地形高度(单位：m)

2结果分析

2.1地形重力波对纬向风场的影响

Alpert[18]和McFarlane[19]等研究表明，引入重力波拖曳后，大气的风场和温度场将发生调整，地形复杂区域更为显著。为了进一步探究复杂地形激发出的地形重力波对风场的影响，设计了不考虑重力波拖曳的控制试验(Ctrl)和不同拖曳力系数(GWDO)下的4组敏感性试验，对2007年7月3日00时至10日00时发生在我国的降水天气过程进行模拟研究。

图2给出在复杂地形区沿100°E一周平均的纬向风纬度—高度剖面，敏感性试验和控制试验与作为实况的再分析资料进行对比，发现都很好地模拟出西风急流(≥30 m/s)轴的空间位置与形态，急流轴主要位于36°N~44°N的对流层高层(300~100 hPa)，急流核位于40°N、200 hPa处，而10°N~30°N之间的对流层中高层位于东风区，东风区的范围随气压的升高向北倾斜，对流层底层大地形的南北两侧主要为西风气流区。对比引入重力波拖曳后的效果，敏感性试验与控制试验纬向气流的空间结构主要分布特征变化不大，但对风场的强度有较明显的调整。图3为不同拖曳力系数下敏感性试验与控制试验的纬向风差值分布，大地形对纬向风风速有明显的影响，在大地形南侧15°N~20°N对流层高层表现为西风式差值流场，中低层表现为东风式差值流场，而在25°N~45°N大地形上空存在一个倒U型西风式差值流场区，但在30°N~38°N的600~400 hPa为东风式差值流场，这种分布型可能与纬向气流经过大地形时发生的绕流与爬坡有关，使重力波激发的波动能受到地形影响后重新分配。可以看出拖曳力越强产生的纬向风调整越强，由于不同环流背景下，重力波波动能把水平动量传输到波动被吸收或耗散的区域不尽相同，导致不同个例下纬向风调整可能呈现出不同的特征。

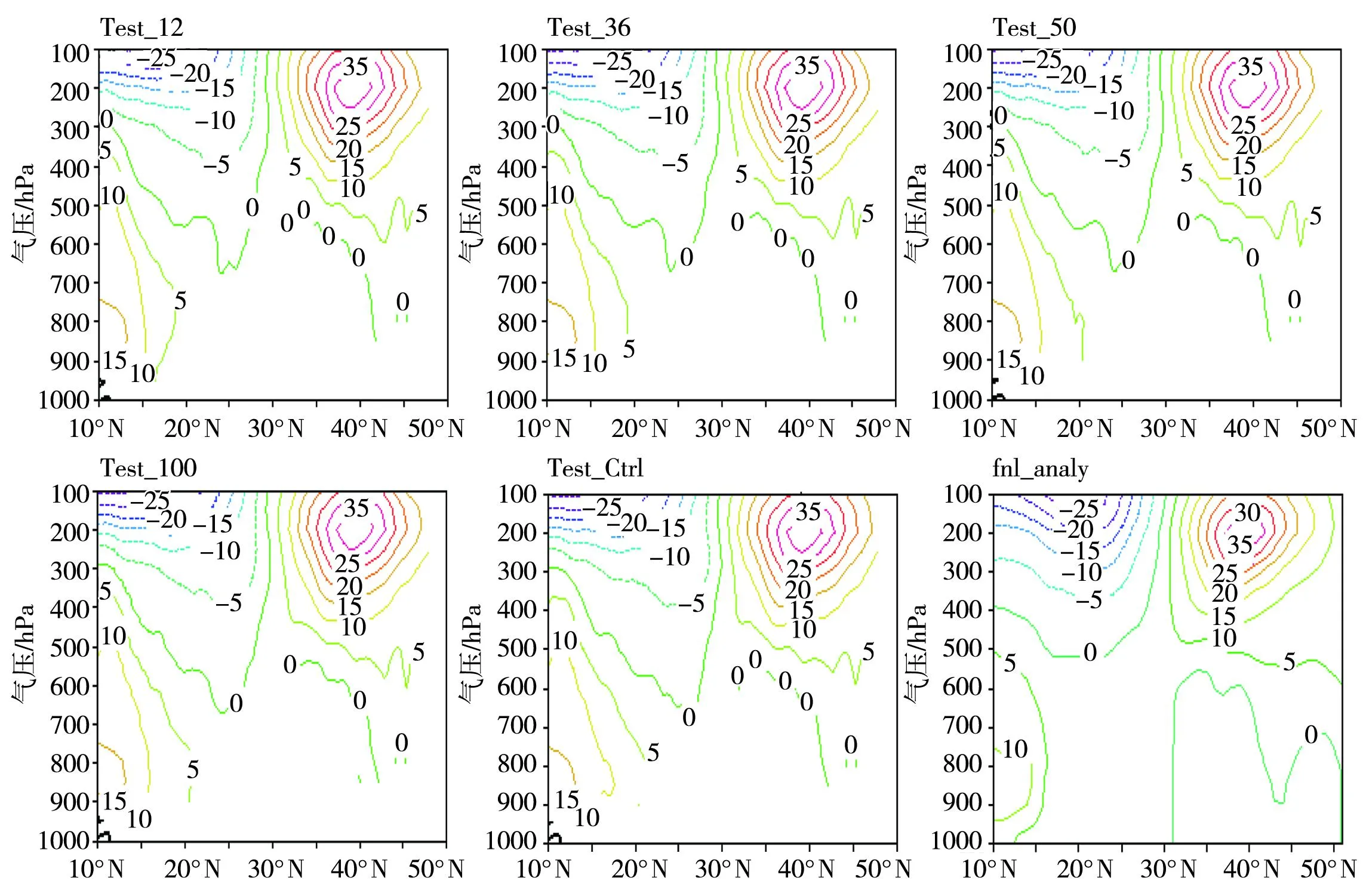
图2　不同敏感性试验、控制试验和实况下沿100°E 7 d平均的纬向风纬度—高度剖面(单位：m/s)

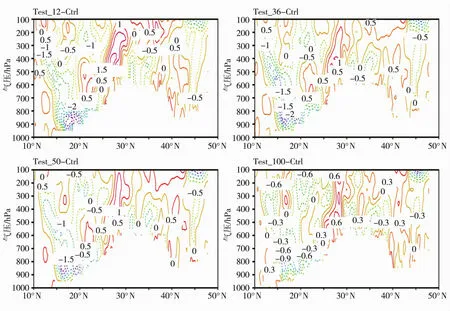
图3　沿100°E 7 d平均的纬向风纬度—高度剖面敏感性试验与Ctrl试验差值分布(单位：m/s)

2.2地形重力波对环流场和降水场的影响

次网格地形重力波拖曳参数化方案对风场的预报有直接的影响。通过对风场的调整，改变水汽输送路径及强度，从而对降水预报产生影响。

为了探究重力波拖曳方案对此次降水过程模拟的改进，图4给出控制试验和不同拖曳力系数下的敏感性试验降水关键区区域平均累计降水量随时间的变化，这里将TRMM降水资料作为实况资料进行对比分析。TRMM降水资料为热带测雨卫星(Tropical Rainfall Measuring Mission，TRMM)星载降水雷达(Precipitation Radar，PR)的3B42RT数据集[20]，分辨率为0.25°×0.25°，TRMM资料的使用为研究降水的日变化提供了较可靠的数据资料[21]。

就降水量而言，前72 h的模拟，控制试验和敏感性试验与实况对比都有较好的一致性，控制试验对降水量模拟略有低估。之后，控制试验明显低估降水量，加入不同拖曳力系数下的重力波拖曳方案试验对降水预报有不同程度改善，降水量随着引入的拖曳力增强而增长。Test_12和Test_36在7月6日和7月7日的预报中较其他试验显示出优势。7月7日之后，随着模拟时间延长，加入重力波拖曳的试验对降水模拟有改善，但降水误差仍被进一步加大。

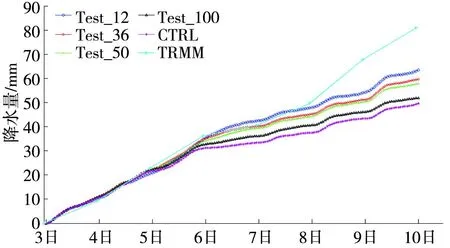
图4　模拟区域(28°N~34°N，100°E~120°E)

图5为TRMM及各试验模拟的2007年7月3日00时至7月10日00时区域平均(28°N~34°N，100°E~120°E)降水随时间的演变，可以看出各试验能较好地模拟出降水随时间的波动特征，但对极端降水各试验都有一定程度的低估，7月7日后模拟的强降水时段与实况也有一定偏差，结果不够理想。

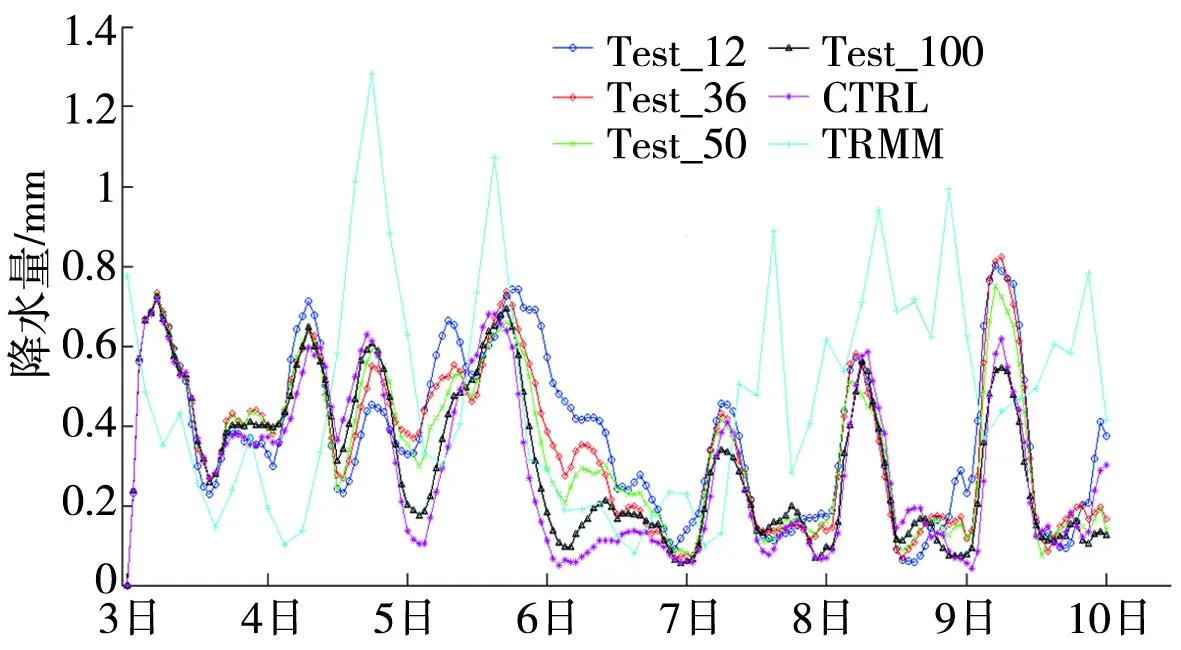
图5　各试验模拟的与TRMM观测的28°N~34°N,

引入不同拖曳力作用下的敏感性试验对模拟结果有一定程度改善，特别是对7月6日和7日的模拟。

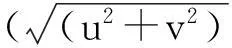
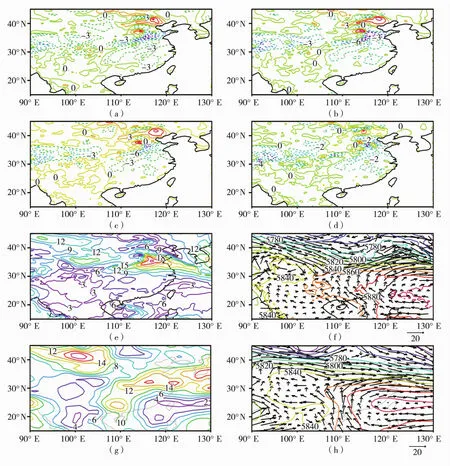
图6　2007年7月6日00时500 hPa GWDO试验Test_12(a)、Test_36(b)、Test_50(c)、

选取典型降水日7月3日、5日、9日，图7、图8、图9给出典型降水日控制试验、敏感性试验及实况降水空间分布。对于起报日的降水分布，由于准确的初始场和前期工作中各方案的调试，各试验都较好地模拟出该日降水的分布(图7)。7月5日00时至6日00时的降水预报(图8)，Test_Ctrl未能模拟出该日的主要降水带，引入GWDO方案后的各试验对降水的预报有显著改善，试验Test_50和Test_100对暴雨及以上的降水区模拟范围偏广且偏北，试验Test_12和Test_36相对较好。7月9日00时至10日00时的降水预报(图9)，各试验都较好地模拟出30°N附近东西向的带状降水分布，但对几个强降水中心雨量都有一定程度低估，试验Test_12和Test_36相对于Test_Ctrl有一定程度的改善。此次降雨雨带主要集中在28°N~34°N区域内，不同拖曳力系数下的敏感性试验对降水预报较Ctrl试验都有不同程度的优化，随着预报时次的推移，引入的拖曳力越强，对降水预报的改善越好。

图10给出7月5日沿33°N日平均的垂直速度场分布，可以看出实况在青藏高原以东为上升运动区，垂直上升运动有2个主要的强对流区，气流越过大地形后，背风坡气流受绝对位涡守恒约束更易激发出上升运动，在大环流背景场作用下，使108°E附近区域从对流层中低层到高层都表现为旺盛的对流运动，另一个强对流区位于114°E以东地区。Ctrl试验对108°E附近的强对流上升区有较好的模拟，但明显低估了114°E以东地区的上升运动，导致控制试验在降水预报中的偏差；在不同重力波拖曳系数下的试验中，Test_50和Test_100由于引入的拖曳力过小，对垂直速度场的改进不理想，Test_12和Test_36对垂直速度场的调整显示出较好的效果，不仅模拟出108°E附近区域的对流上升区，同时对114°E以东地区的对流运动的模拟有较好的改进，从而使降水模拟也有了较好的改善。综合降水和流场，Test_12相对其它试验更有优势。垂直上升运动是降水形成的重要触发机制，重力波拖曳方案的引入通过对风场的调整，改进垂直速度场的模拟效果，进而提高预报的准确性。刘蕾等[11]利用地形重力波参数化方案对华南地区的暴雨发生机制进行研究，也发现重力波参数化方案能使上升运动增强，能很好地模拟暴雨的中心位置和强度。这与本文的结论一致，也加强了该结论的可信性。

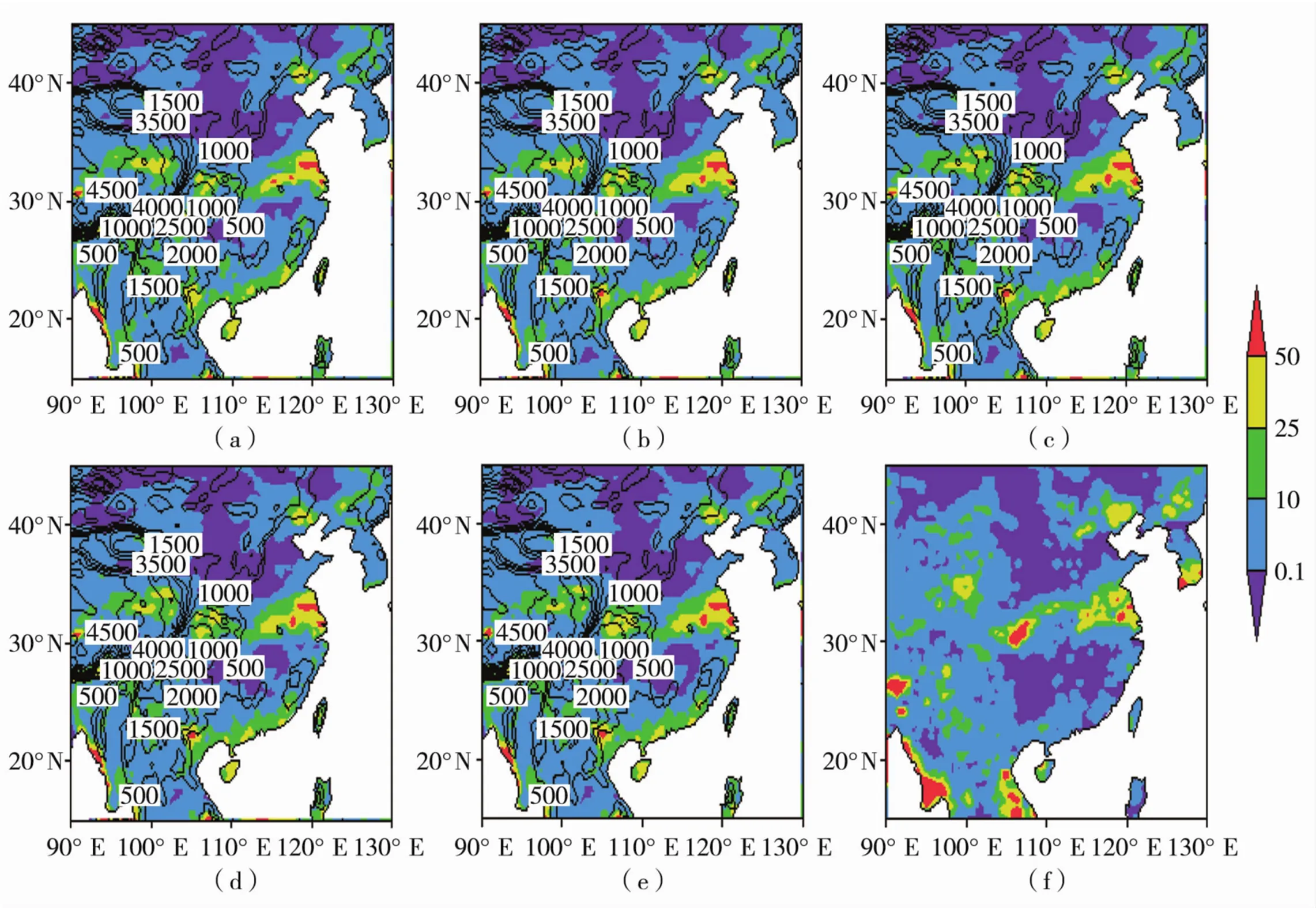
图7　2007年7月3日00时至4日00时Test_12(a)、Test_36(b)、Test_50(c)、Test_100(d)、

图9　2007年7月9日00时至10日00时Test_12(a)、Test_36(b)、Test_50(c)、Test_100(d)、

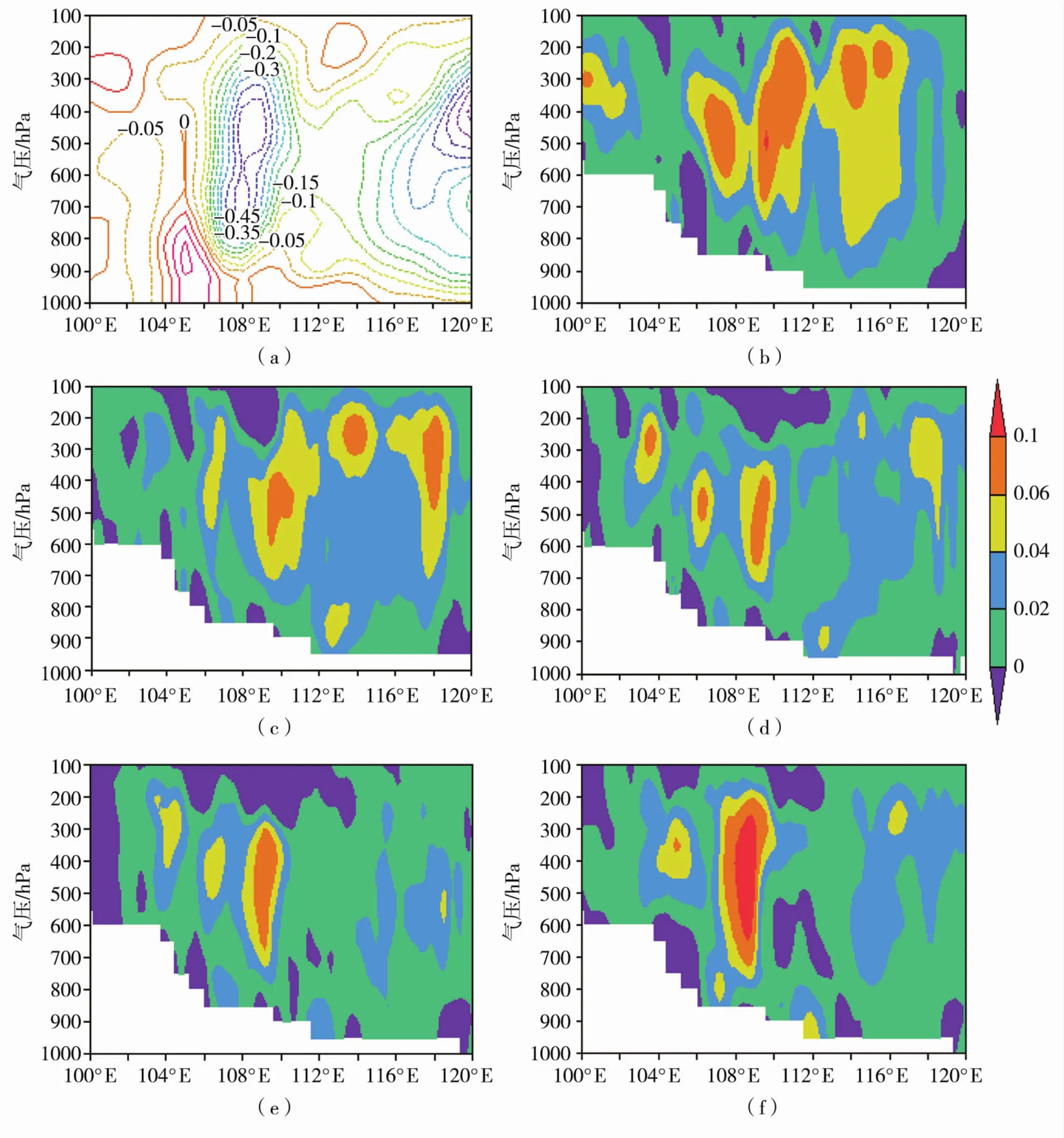
图10　2007年7月5日沿33°N 观测(单位：Pa/s)与模拟 (单位：m/s)的日平均垂直速度

图11给出各试验模拟的7月5日850 hPa水汽输送矢量，各试验都模拟出了孟加拉湾和南海旺盛的水汽向我国东南沿海和内陆的输送，Ctrl试验模拟的水汽输送较引入GWDO方案后的各试验偏强，图11f给出试验Test_12与Ctrl试验水汽输送矢量的差值，主要偏差出现在从四川盆地到山东半岛东北西南向的水汽输送带，这刚好与降水带相一致，特别是30°N、110°E附近为水汽调整的极值区，自南向北的水汽输送带经地形重力波作用后在该地区向北输送急剧减弱，使旺盛的水汽在该地区汇聚，加上垂直运动的触发，该地区出现了高强度的降水，对应该区域形成了强降水中心(图8f)，充沛的水汽条件是降水形成的重要原因之一，引入GWDO方案后对水汽输送进行调整，延缓了水汽输送，对模拟结果有了较好的优化。

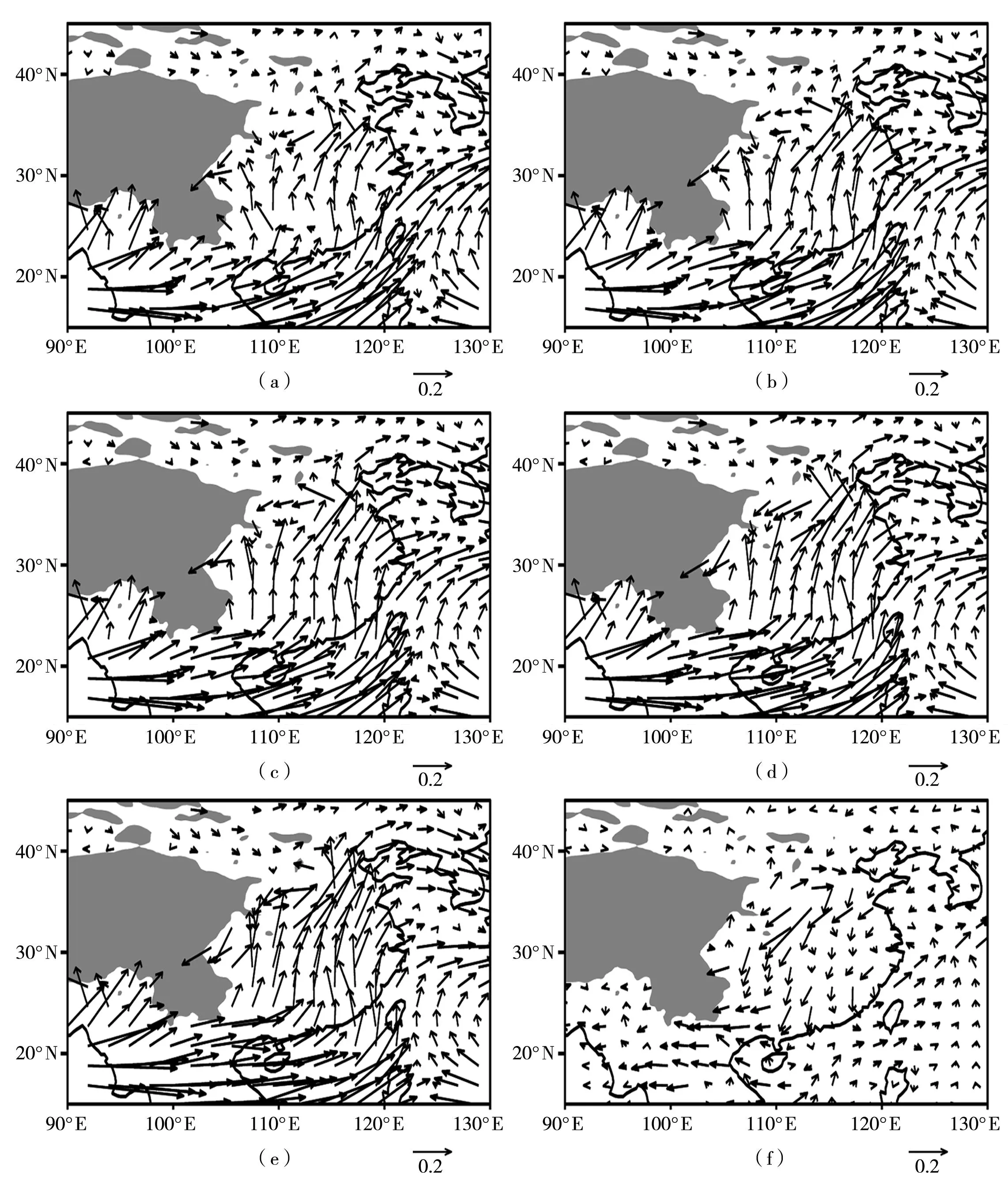
图11　2007年7月5日850 hPa水汽输送矢量(单位：m·g·s-1·kg-1)

为进一步探究引入GWDO方案对降水落区强度的影响，同时考虑GWDO方案对后期降水模拟的效果改善显著，图12、图13给出5日与9日不同拖曳力系数下各试验与控制试验的降水差值分布。总体来讲，随着预报时间延长，引入的拖曳力越强，对降水预报的改善越好。对于7月5日00时至6日00时的预报(图12)，通过水汽输送的调整，使雨区北部降水减弱，南部降水加强，有效地改善了降水带偏北的偏差，使降水落区更加接近实况。7月9日00时至10日00时的预报(图13)，低估了强降水区的降水，试验Test_12中强地形重力波拖曳作用对30°N附近的降水带有明显的改善。Test_12试验与Test_Ctrl试验的差值(图13a)分布与7月9日的实况降水区(图9f)有很好的一致性，地形重力波作用对降水的调整使强降水带的降水一定程度得以显现，降水分布更接近实况。

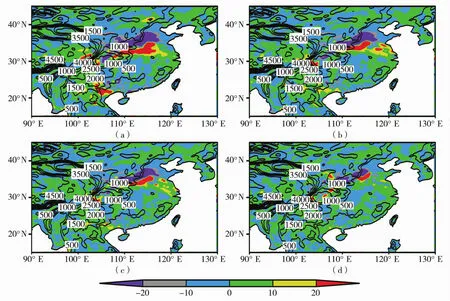
图12　2007年7月5日00时至6日00时敏感性试验与控制试验降水差值(单位：mm)

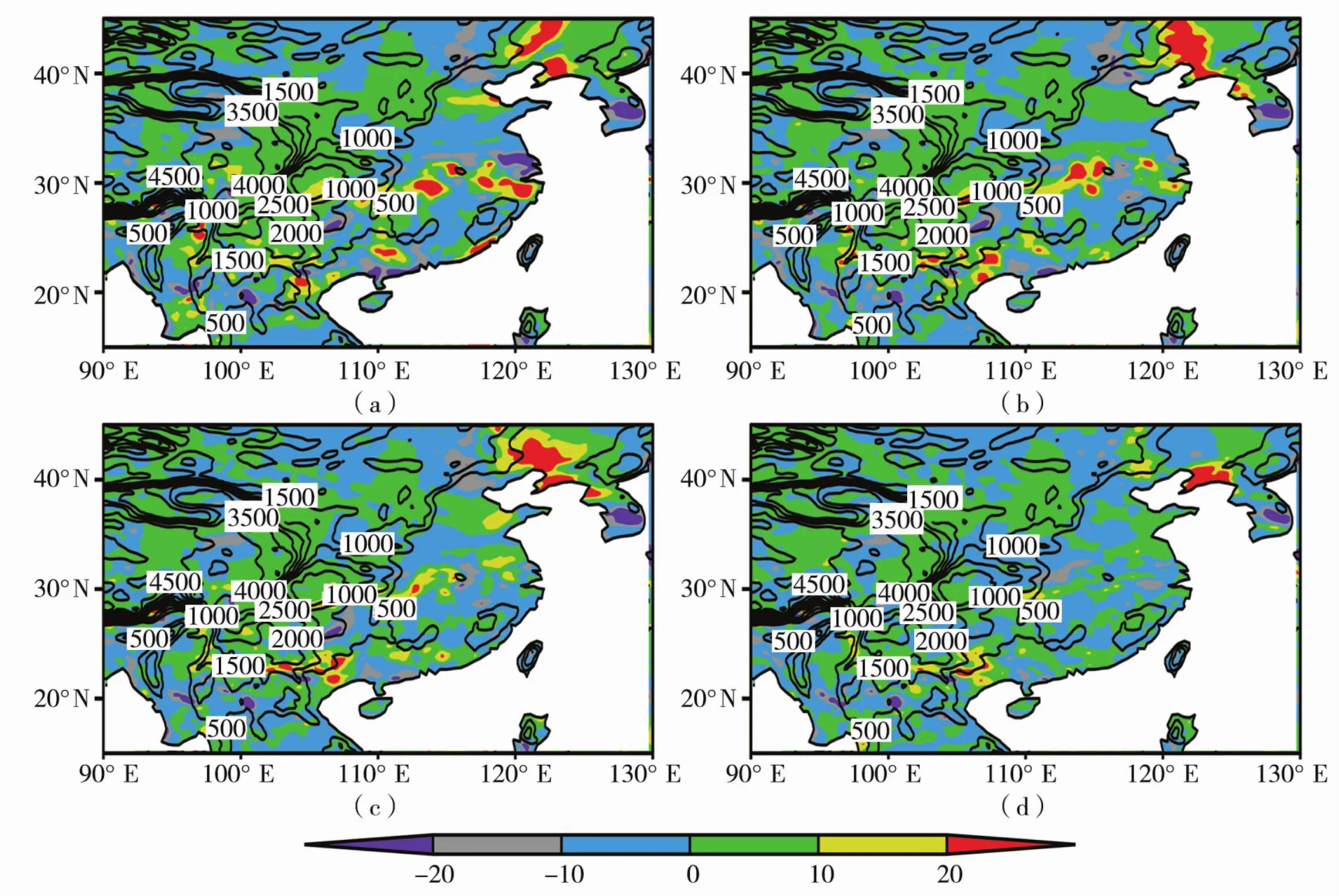
图13　2007年7月9日00时至10日00时敏感性试验与控制试验降水差值(单位：mm)

3结论

(1)GWDO参数化方案的引入能有效地调整纬向气流，缓解纬向风场偏差，大地形的上空存在一个倒U型西风式差值流场区，拖曳力越强，所产生的纬向风差值越大。

(2)GWDO参数化方案的引入对降水预报前期的影响并不明显，但对后期的降水预报有较好的改善，特别是在后期引入重力波拖曳后对降水的订正，即敏感性试验与控制性试验降水差值分布，与实况降水分布范围十分接近，引入重力波拖曳对降水预报有很好的订正效果，同时对降水落区和强度也有较好的调整，使雨区北部降水减弱，南部降水加强，有效地改善了降水带偏北的偏差，使降水落区更加接近实况。随着预报时次的推移，引入的拖曳力越强，对降水预报的改善越显著。

(3)GWDO参数化方案的引入在中期预报中对500 hPa的强风速带有削弱作用，风速大值区与风速削弱区有很好的一致性，对提高形势场预报的准确性有很好的效果。

(4)GWDO参数化方案的引入地形重力波拖曳力通过对环流场、水汽输送带的调整，使水汽输送更精准；随着重力波拖曳力的增强，使7月5日垂直速度场的预报从单强对流中心变为双强对流中心，与实况垂直速度分布相一致，提高了预报准确率，在多要素的共同作用下延长了预报时长。

参考文献:

[1] Wallacc J M, Tibaldi S, Simmons A J. Reduction of systematic errors in the ECMWF model through the introduction of an envelope orography[J]. Quarterly Journal of the Royal Meteorological Society,1983,109:683-717.

[2] Tibaldi S. Envelope orography and maintenance of quasi-stationary waves in the ECMWF model[J]. Advances in Geophysical and Environmental,1986,29:339-374.

[3] 刘华强，钱永甫. 包络地形和重力波拖曳对区域气候模拟效果的影响[J]. 大气科学，2001,25(2):209-220.

[4] Boer G J, Mcfarlance N A, Laprise R, et al. The Canadian Climate Centre spectral atmospheric general circulation model[J]. Atmosphere-Ocean, 1984,22:397-429.

[5] Palmer T N, Shutts G J, Swinbank R. Alleviation of a systematic westerly bias in circulation and numerical weather prediction models through an orographic gravity-wave-drag parameterization[J]. Quarterly Journal of the Royal Meteorological Society ,1986,112:1001-1039.

[6] 乌元康. 地形重力拖曳效应的参数化[J]. 气象科技，1987(4):31-33.

[7] Kim J, Arakaw A A. Improvement of orographic gravity wave parameterization using a mesoscale gravity wave model[J]. Journal of the Atmospheric Sciences,1995,52:1875-1902.

[8] Hong S Y, Choi J, Chang E C, et al. Lower-tropospheric enhancement of gravity wave drag in a global spectral atmospheric forecast model[J]. Weather and Forecasting, 2008,23:523-531.

[9] 覃卫坚，寿绍文，李启泰，等. 影响惯性重力波活动规律的动力学因子研究[J]. 高原气象，2007,26(3):519-524.

[10] 王文，刘佳，蔡晓军. 重力波对青藏高原东侧一次暴雨过程的影响[J]. 大气科学学报，2011，(34):737-747.

[11] 刘蕾,丁治英,常越，等. WRF中地形重力波参数化方案在一次华南暖区暴雨形成机制分析中的应用[J]. 气象科技，2012(2):232-240.

[12] 刘蕾. 一次暖区暴雨形成机制的数值试验与诊断分析[D]. 南京:南京信息工程大学，2011.

[13] 王莉. GWDO参数化方案以及地形对一次大别山暴雨的影响研究[D]. 南京:南京信息工程大学，2011.

[14] 刘佳，王文. 一次暴雨过程的重力波特征分析[J].干旱气象,2010,28(1)：65-70.

[15] 徐国强，杨学胜，黄丽萍，等. GRAPES中地形重力波拖曳物理过程的引进和应用试验[J]. 气象学报,2010,68(5):631-639.

[16] McFarlane N A. The effect of orographically excited gravity wave drag on the general circulation of the lower stratosphere and troposphere[J]. Journal of the Atmospheric Sciences, 1987,44:1775-1800.

[17] Mesinger F, Collins W G. Review of the representation of mountains in numerical weather prediction models[R].Proc Seminar/Workshop on observation, theory and modeling of orographic effects. 2:ECMWP, Shinfield Park, Reading, U K, 15-20 September 1986.1-28.

[18] Alpert J C, Kanamitsu M, Caplan P M, et al. Mountain induced gravity wave drag parameterization in the NMC medium-range forecast model[A]. Preprints, Eighth Conf on Numerical Weather Prediction, Baltimore, MD, Amer Metero Soc,1988.726-733.

[19] McFarlane N A. The effect of orographically excited gravity wave drag on general circulation of the lower stratosphere and troposphere[J].J Atmos Sci,1987,44:1775-1800.

[20] Kummerow C D, Simpson J, Thiele O, et al. The status of the Tropical Rainfall Measuring Mission(TRMM) after two years in or-bit[J]. Journal of Applied Meteorology and Climatology, 2000,39(6): 1965-1982．

[21] Sorooshian S, Gao X, Hsu K, et al. Diurnal variability of tropical rainfall retrieved from combined GOES and TRMM satellite information[J]. Journal of Climate, 2002,15(9):983-1001.

Application of Orographic Gravity Wave Drag Parameterization Scheme and Different Drag Forces Test in WRF Model

AI Kai1, ZHENG Yiqun1，2, CHEN Haowei1

(1.InstituteofMeteorologyandOceanography,PLAUniversityofScienceandTechnology,Nanjing211101,China;2.JiangsuCollaborativeInnovationCenterforClimateChange,Nanjing210093,China)

Abstract:The orographic gravity wave drag (GWDO) parameterization scheme was introduced into WRF model firstly, and the different drag force sensitivity tests were designed to simulate the rainfall weather process occuring in China the period of Meiyu in the Yangtzi River and Huaihe River valleys turning to rainy season in North China from 00:00 UTC 3 July to 00:00 UTC 10 July 2007 by using the Weather Research and Forecast (WRF V3.2 version) model in this paper. Five groups of numerical experiments were designed, including one control test (Ctrl) without GWDO scheme and four groups of sensitive tests with the GWDO scheme into consideration but the drag force was different. The results show when the orographic gravity wave drag was applied into the WRF model, the circulation field, vapor transport belt and the vertical velocity field were improved efficiently, and the phenomenon of forecasted wind speed being a bit strong had been mitigated, the zonal wind deviation was redressed also in some degree, and the distribution and intensity of rainfall were improved well at the same time.With the simulation time going on, the stronger drag force introduced into WRF model was, the more signficant improvement on precipitation simulation was.

Key words:georgraphy; GWDO parameterization schemes; numerical experiment

中图分类号：P456.7

文献标识码：A

文章编号：1006-7639(2016)-01-0125-11

doi:10.11755/j.issn.1006-7639(2016)-01-0125

作者简介：艾凯(1991-), 男，硕士研究生，主要从事全球变化和气候模拟的研究. E-mail: aikai91@126.com

基金项目：国家重点基础研究发展计划(973计划)项目(2010CB428505)和国家自然科学基金项目(41275012,41475069)共同资助

收稿日期：2015-07-22；改回日期：2015-10-25

艾凯，郑益群，陈浩伟.WRF模式中地形重力波参数化方案应用及不同拖曳力试验[J].干旱气象，2016，34(1)：125-135, [AI Kai, ZHENG Yiqun, CHEN Haowei. Application of Orographic Gravity Wave Drag Parameterization Scheme and Different Drag Forces Test in WRF Model[J]. Journal of Arid Meteorology, 2016, 34(1):125-135], doi:10.11755/j.issn.1006-7639(2016)-01-0125