基于SIMULINK的PEM燃料电池系统模型建立及其仿真分析

夏发银，陈　玉，宾　洋

1.安徽工程大学机械与汽车工程学院，安徽芜湖，241000；

2.北京工业大学环境与能源工程学院，北京，100124



基于SIMULINK的PEM燃料电池系统模型建立及其仿真分析

夏发银1，陈玉1，宾洋2

1.安徽工程大学机械与汽车工程学院，安徽芜湖，241000；

2.北京工业大学环境与能源工程学院，北京，100124

摘要：运用MATLAB/SIMULINK软件搭建出PEM燃料电池系统的模型，结合PEM燃料电池系统机理模型的准确性和经验模型的简便性，建立了一个半经验模型，通过整合半经验模型中的公式，在SIMULINK中搭建模型进行仿真。对影响PEM燃料电池性能的几个主要因素(电堆温度、工作压力、交换膜湿度)和PEM燃料电池的动态特性进行了分析。结果表明：电堆温度的升高、工作压力的增加以及交换膜湿度的提高分别在不同程度上提高了PEM燃料电池的性能。该模型可以模拟PEM燃料电池启停、负载电流增加与减少时，整个系统的动态特性和效率的变化。

关键词：PEM燃料电池；SIMULINK建模；半经验模型；动态仿真

1问题的提出

PEM燃料电池系统具有非线性和时变特性，其模型的建立和控制是目前学界研究的一个热点[1]。PEM燃料电池系统模型建立通常分为机理建模和经验建模[2]。其中机理建模主要有Rowe模型[3]、Berning模型[4]等，但这些模型非常复杂，不易于控制策略研究。为解决这一问题，出现了很多基于参数辨识方法的经验模型，如Genetic Algorithms模型[5]、Harmony Search模型[6]、Differential Evolution模型[7]等。本文以Pukrushpan的模型[8]为基础，在SIMULINK中建立以负载电流和空压机控制电压为输入、电堆电压为输出的PEM燃料电池系统半经验模型。

2PEM燃料电池系统的电化学模型

PEM燃料电池系统主要由空压机、供排气管道、氢气供应设备、电堆以及电堆阴阳极和膜组成的膜电极部分(图1中框线内部分)共同构成(图1)。

图1　燃料电池系统构成

2.1空气压缩机模型

压缩机输出端的空气温度可通过式(1)进行计算，电机需要的转矩由热动力学等式(2)计算得到[9]。

(1)

(2)

完整的空气压缩机的电机动态性能由等式(3)描述：

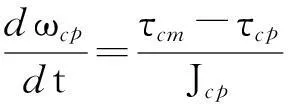
(3)

空气压缩机的电机转矩可以由电机的静态等式(4)获得：

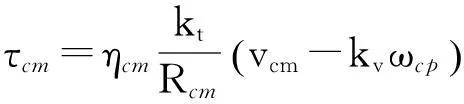
(4)

2.2进排气管道模型

对于进气管道来说，流入管道内的气体流速等于空气压缩机输出端的气体流速Wcp，流出管道的气体流速为Wsm,out，由于进气管道的压力与阴极压力相差较小，所以

(5)

公式(6)和(7)分别通过质量和压力与流速的关系来描述进气管道：

(6)

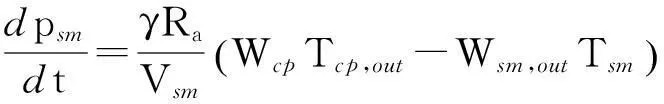
(7)

由于空气通过排气管道离开燃料电池时温度相对较低，所以在排气管道中的温度变化可以忽略不计。公式(8)通过压力与流速的关系来描述排气管道：

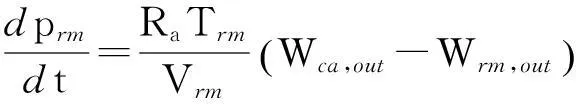
(8)

2.3电堆电压模型

PEM燃料电池的理想电势(E)为1.229V。但是，由于不可逆的电压损失，实际情况下，电池电压会随电流密度的增加而下降。燃料电池的不可逆损失过程常被称为极化过电势或者过电压，主要由活化极化、欧姆极化和浓差极化导致的[10]。活化极化主要在低电流密度时起作用，浓差极化主要在高电流密度时起作用，而欧姆极化则贯穿整个过程。PEM燃料电池电堆电压模型如下：

vfc=E-vact-vohm-vconc

(9)

vst=nvfc

(10)

2.4阴极模型

该阴极模型描述了电堆阴极内部的气体特性。模型是建立在质量守恒原理和空气热动力学原理的基础上的。利用质量的连续性来表示阴极中的氧气、氮气和水，用下面三个状态方程来描述阴极中氧气、氮气和水的变化：

(11)

(12)

(13)

2.5阳极模型

在阳极模型中，氢气是由普通氢气罐提供。假设通过阀门来控制阳极的氢气流，以保证相对较小的阴阳两极之间的压力差。假设阴极通道流动阻力远大于阳极通道，则可以保证提供充足氢气所需的压力。与阴极模型类似，阳极气体和水的平衡条件决定了氢气压力和阳极氢气湿度。用下面两个状态方程来描述阳极中氢气和水的变化：

(14)

(15)

2.6交换膜水化模型

跨越交换膜的水进行交换后，通常出现两种不同的现象：

(i)水分子如果要是从阳极穿过交换膜流到阴极，则必须要有氢质子的参与，这种现象称为电渗阻力。

随着大数据时代的发展，移动网络设备已经普及，手机应用软件已经能够为人们提供所需的大部分信息服务。财务信息化服务由于缺少相应的移动端模式，致使财务处理局限于PC端、报销流程半自动化、数据缺乏共享，已经不能满足学校发展和师生对财务事项办理的需求。

(16)

(ii)由于阳极的氢气和阴极的氧气与氮气拥有不同湿度，势必会产生一个水溶度的梯度，此梯度则会引起阴阳极两边的水反向扩散。

(17)

结合电渗阻力和反向扩散，水流穿过膜可以写成以下方程式(水从阳极流到阴极为正)：

(18)

以下方程式表示通过交换膜的水总流速：

Wv,member=Nv,member×Mv×Afc×n

(19)

3SIMULINK建模与仿真

根据(1)~(19)式，建立PEM燃料电池系统的SIMULINK模型。模型的输入为负载电流和空气压缩机控制电压，输出为电堆电压(图2)。

稳态仿真可以分析影响燃料电池极化曲线的相关因素，如电堆温度、工作压力和交换膜湿度等(图3)。

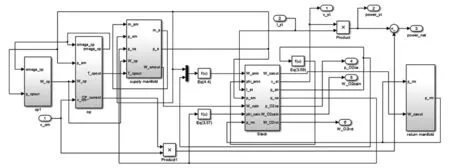
图2　PEM燃料电池系统SIMULINK模型

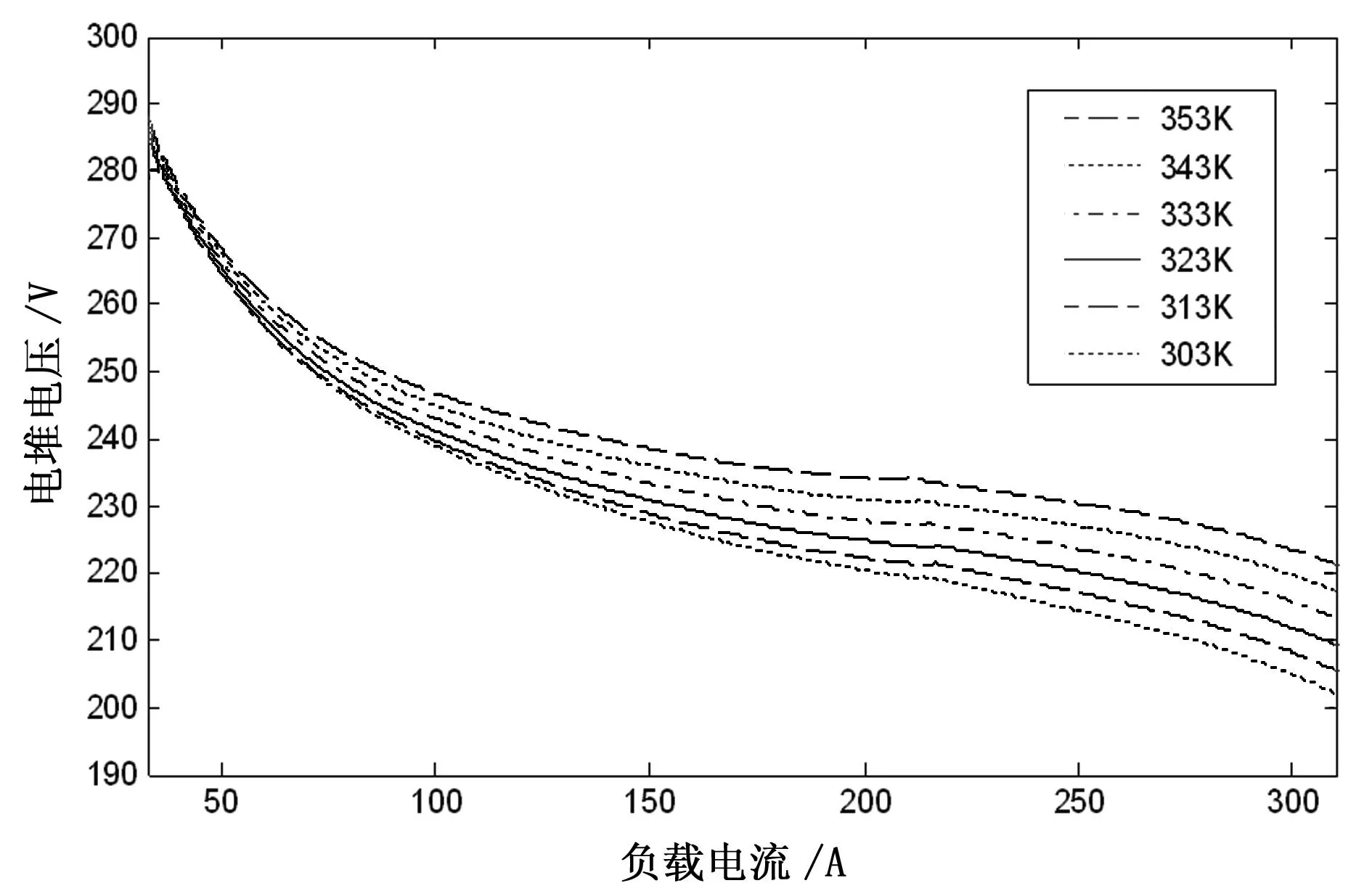
图3　温度对燃料电池极化曲线的影响

图3表明，在负载电流、工作压力、交换膜湿度相等情况下，电堆温度越高，电堆电压就越高，其输出功率也就越高。但是，目前PEM燃料电池所使用的交换膜基本是杜邦公司的Nafion膜，其耐温能力有限，正常运行温度为0℃~80℃(273K~353K)。超过此温度，其热稳定性和质子传导性能急剧下降，对燃料电池的性能影响极大。因此应该控制电堆温度接近80℃，而不能超过80℃。图4表明，在负载电流、电堆温度、交换膜湿度相等情况下，工作压力越大，电堆电压就越高，其输出功率也就越高。但是，在实际当中，由于空压机控制工作压力，电压升高会加大空气压缩机的功率损耗，因此应将电堆的工作压力控制在一定的范围内。

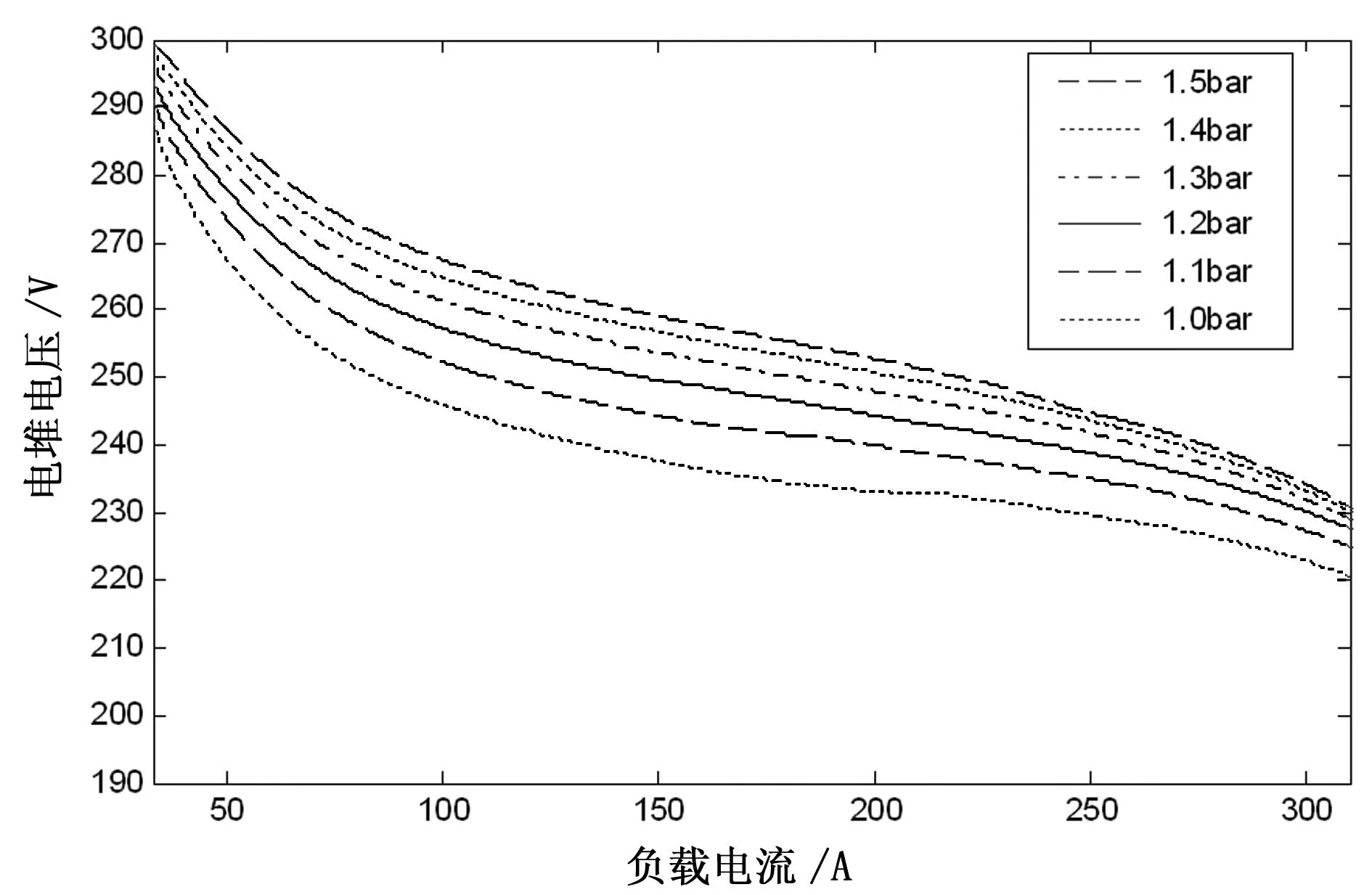
图4　工作压力对燃料电池极化曲线的影响

图5表明，在负载电流、电堆温度、工作压力相等的情况下，交换膜湿度越高，电堆电压就越高，其输出功率也就越高。但是，当湿度为100%时，可能会在电堆内部集聚大量的液态水，影响正常的电化学反应，甚至会淹没电极导致燃料电池不能正常的工作。因此，应该根据实际情况，调节进入燃料电池电堆内的气体湿度，尽量地把湿度控制在接近或达到100%，而不产生过量的液态水。

图5　交换膜湿度对燃料电池极化曲线的影响

3.2动态仿真

根据上述结论，设置动态仿真的参数如下：电堆温度为80℃，工作压力为大气压1bar，交换膜湿度为100%。如图6，输入部分采用阶跃变化，并且空压机控制电压跟随负载电流的变化同步变化。

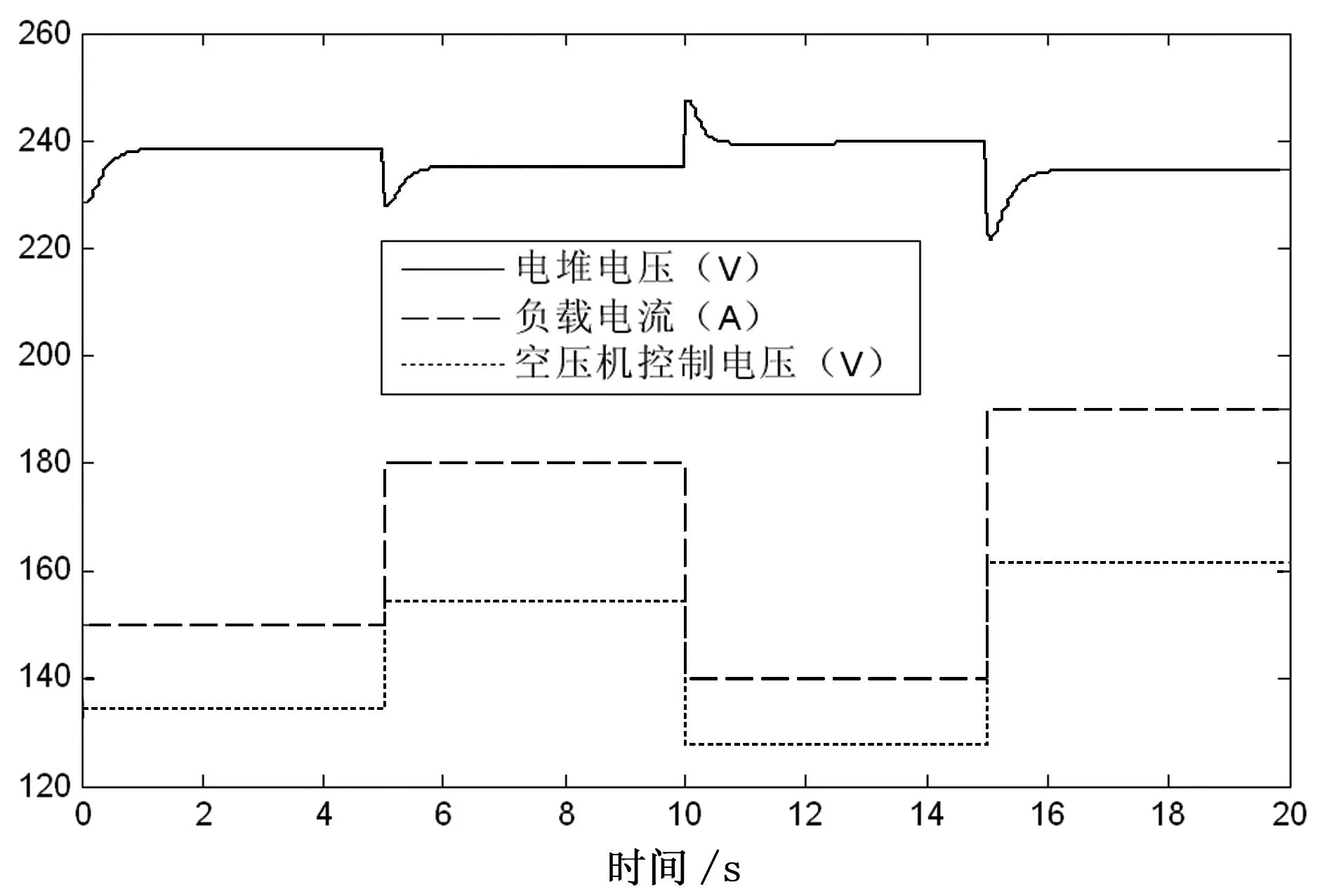
图6　动态响应中电流与电压的变化

从图6可以看出，随着负载电流的增加，电堆电压在下降。由于负载电流增加时会产生活化极化、欧姆极化和浓差极化，这3种不可逆的电压损失导致了电堆电压随负载电流的增加而下降。反推可知，随着负载电流的减少，电堆电压会逐渐上升。

但是，在电堆电压下降和上升的初期，会有短暂的电压下过冲和电压上过冲现象。电压下过冲现象是由于当负载电流突然增加时，大量氢离子传递到阴极，在此过程中造成大量水分子由阳极向阴极流动，使得阳极短时失水，电池内阻突然上升，从而产生电压突然下降，即电压下过冲现象。电压上过冲现象与前述现象相反。

电堆功率即是电堆电压与负载电流之乘积，它是衡量燃料电池性能的重要参数，也是燃料电池的标称功率。但是，作为对PEM燃料电池整个系统的研究，还应该考虑整个系统的内部消耗，也就是所谓的寄生功率。在PEM燃料电池系统中，空气压缩机的功率消耗是最主要的寄生功率，本文建立的模型忽略诸如加湿系统、冷却系统以及控制阀门等的功率消耗。电堆功率与寄生功率之差就是电堆净功率。

图7　动态响应中电堆功率、净功率与寄生功率变化

由图7可知，电堆功率于33.55~44.57 KW时，寄生功率大约占比8.03%~11.34%，并且寄生功率在整个系统中所占的比例会随着电堆功率的增加而增大。对于PEM燃料电池系统来说，系统的效率即是电堆净功率比上电堆功率。表1列出了各个不同电堆功率所对应的系统效率的仿真结果。

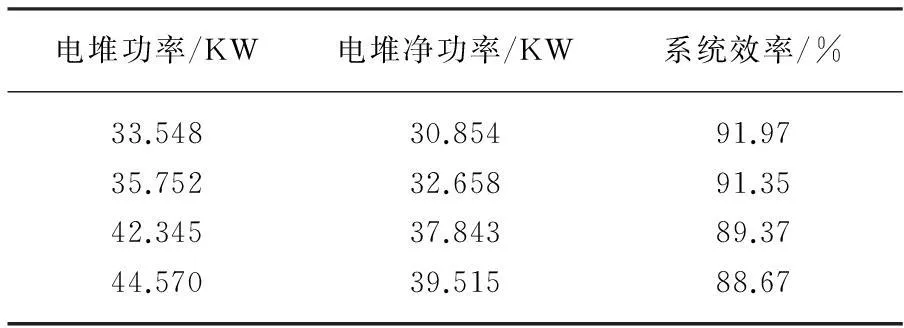
表1　不同电堆功率对应的系统效率

由表1可知，PEM燃料电池系统的效率随着电堆功率的增加而降低。这为以后PEM燃料电池系统的控制研究提供了基础性资料。

4结 论

(1)建立了完整的PEM燃料电池系统模型，可以对其进行相关的稳态和动态仿真；

(2)分析了影响PEM燃料电池性能的因素，即电堆温度、工作压力、交换膜湿度，这样可以更有针对性地优化其性能；

(3)通过动态仿真，可以模拟PEM燃料电池启停、负载电流增加与减少时，整个系统的动态特性和效率的变化，是PEM燃料电池系统控制及其混合电源系统控制的基础。

参考文献：

[1]杨忠君，樊立萍，宗学军．基于DHP方法的PEM燃料电池优化控制器设计[J]．电源技术，2014(11)：2007-2009

[2]衣宝廉．燃料电池：原理·技术·应用[M]．北京：化学工业出版社，2003：1-2

[3]Wang Caisheng,Nehrir M H,Shaw S R.Dynamic models andmodel validation for PEM fuel cells using electrical circuits[J].IEEE Transaction on Energy Conversion,2005,20(2):442-449

[4]Berning T,Lu D M,Djilali N D. Three-dimensionalcomputational analysis of transport phenomena in a PEM fuelcell[J].J Power Sources,2002,106(1/2):284-294

[5]Zhang Li,Wang Ning.An adaptive RNA genetic algorithm for modeling of proton exchange membrane fuel cells[J].International Journal of Hydrogen Energy,2013,38(1):219-228

[6]Karimi M,Askarzadeh A,Rezazadeh A.Using tournament selection approach to improve harmony search algorithm for modeling of proton exchange membrane fuel cell[J].International Journal of Electrochemical Science,2012(7):6426-6435

[7]Oguz Emrah Turgut,Mustafa Turhan Coban. Optimal proton exchange membrane fuel cell modelling based on hybrid Teaching Learning Based Optimization-Differential Evolution algorithm[J].Ain Shams Engineering Journal 2015(5):1-14

[8]Jay T Pukrushpan,Anna G Stefanopoulou,Huei Peng.Control of fuel cell breathing[J].IEEE Control Systems Magazine,2004,4:30-46

[9]Geyerh K,Ahluwaliar K,KumarR.Dynamic response of steam-reformed,methanol-fueled,polymer electrolyte fuel cell systems[C]//Proceedings of the 31st Intersociety Energy Conversion Engineering Conference,1996:1101-1106

[10]彭飞．质子交换膜燃料电池系统建模与控制研究[D]．长沙：中南大学信息科学与工程学院，2013：17-23

中图分类号：TM911.4

文献标识码：A

文章编号：1673-2006(2016)01-0102-04

作者简介：夏发银(1987-)，安徽合肥人，在读硕士研究生，主要研究方向：燃料电池模型建立及其混合能源控制策略。

收稿日期：2015-09-10