NORMAL FAMILIES OF MEROMORPHIC FUNCTIONS WITH SHARED VALUES∗
2016-04-18WeiCHEN陈玮DepartmentofMathematicsShandongUniversityJinan250100ChinaEmailweichensdu126comHonggenTIAN田宏根SchoolofMathematicsScienceXinjiangNormalUniversityUrumqi830054ChinaEmailtianhgxjnueducnPeichuHU扈培础DepartmentofMathemat
Wei CHEN(陈玮)Department of Mathematics,Shandong University,Jinan 250100,ChinaE-mail:weichensdu@126.comHonggen TIAN(田宏根)School of Mathematics Science,Xinjiang Normal University,Urumqi 830054,ChinaE-mail:tianhg@xjnu.edu.cnPeichu HU(扈培础)Department of Mathematics,Shandong University,Jinan 250100,ChinaE-mail:pchu@sdu.edu.cn
NORMAL FAMILIES OF MEROMORPHIC FUNCTIONS WITH SHARED VALUES∗
Wei CHEN(陈玮)
Department of Mathematics,Shandong University,Jinan 250100,China
E-mail:weichensdu@126.com
Honggen TIAN(田宏根)
School of Mathematics Science,Xinjiang Normal University,Urumqi 830054,China
E-mail:tianhg@xjnu.edu.cn
Peichu HU(扈培础)†
Department of Mathematics,Shandong University,Jinan 250100,China
E-mail:pchu@sdu.edu.cn
AbstractWe obtain some normality criteria of families of meromorphic functions sharing values related to Hayman conjecture,which improves some earlier related results.
Key wordsmeromorphic function;shared value;normal family
2010 MR Subject Classi fi cation30D30;30D45
∗Received November 17,2014;revised January 23,2015.The second author was supported by Nature Science Foundation of China(11461070).The third author was supported by Nature Science Foundation of China(11271227);PCSIRT(IRT1264).
†Corresponding author:Peichu HU.
1 Introduction and Main Results
Let C be the set of complex numbers and let D be a domain in C,which means that D is a connected non-empty open subset of C.Let M(D)be the set of meromorphic functions de fined in D.For{f,g}⊂M(D),{a,b}⊂P1=C∪{∞},we will write f=a⇒g=b(resp.,f=a⇔g=b)if f−1(a)⊂g−1(b)(resp.,f−1(a)=g−1(b)),and say that f and g share a IM(ignoring multiplicities)if f−1(a)=g−1(a)(see[12]).
Let F be a family in M(D).Montel first obtained a famous normal criterion which states that F is normal in D if each element of F omits three distinct values a,b,c in P1,where the family F is said to be normal in D if any sequence of F must contain a subsequence which locally uniformly spherically converges to a meromorphic function or∞in D(see[7,12]).
Later,Carathéodory[2]relaxed the fixed values a,b,c in Montel’s theorem to“wandering”constants af,bf,cfdepending on f∈F such that their spherical distances have a uniform lower bound ε,that is,
(i)min{σ(af,bf),σ(af,cf),σ(bf,cf)}≥ε for some positive real number ε.
The de finition of the spherical distance σ(x,y)between x∈P1and y∈P1can be found in[1].
According to the idea of Carathéodory,Singh and Singh[13]generated a result of Pang and Zalcman[11]by proving that F is normal in D if each f∈F satisfies f=0⇔f′=0 and f=cf⇔f′=bf,where cf,bfare nonzero complex numbers such that spherical distances of 0,bf,cfhave a uniform lower bound ε,that is,
(i)’min{σ(0,bf),σ(0,cf),σ(bf,cf)}≥ε for some positive real number ε,
and such that
Moreover,Grahl[6]corrected a gap of the proof of another similar result in the paper of Singh and Singh[13].
We improve the normality criteria related to normality conjecture due to Hayman[7]which was proved by several authors(see[3,5,9])based on the ideas of shared values as follows:
Theorem 1.1Let n be a positive integer and let F be a family in M(D)such that each element f in F satisfies fnf′=αf⇔f′=bffor nonzero complex numbers αf,bf.If there exists cf∈C satisfyingfor each f∈F such that(i)’and(ii)hold,then F is normal in D.
Obviously,Theorem 1.1 implies directly the following fact:
Corollary 1.2Let n be a positive integer and take nonzero complex numbers α,b withThen a family F in M(D)is normal in D if each f∈F satisfies fnf′=α⇔f′=b.
By weakening the conditions in Theorem 1.1,we can obtain the following result:
Theorem 1.3Let n be a positive integer and let F be a family in M(D)such that each element f in F satisfies
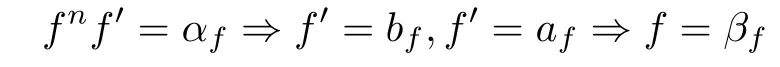
for nonzero complex numbers af,bf,αf,βf.If there exists cf∈C satisfyingfor each f∈F such that(i)holds and such that
Corollary 1.4Let n be a positive integer and take four nonzero complex numbers a,b,α,β such that a,b,c are distinct with cn+1=α.Then a family F in M(D)is normal in D if each f∈F satisfies fnf′=α⇒f′=b and f′=a⇒f=β.
2 Some Lemmas
In order to prove our results,we need the following lemmas.
Lemma 2.1(see[10,14])Let k be a positive integer and let F be a family in M(D)such that each f∈F has only zeros of multiplicity at least k.If F is not normal at z0∈D,then for each real number α with−1<α<k,there exist a sequence{zn}in D converging to z0,a sequence{ρn}of positive numbers converging to 0,and a sequence{fn}in F such that functionslocally uniformly converge to a nonconstant meromorphic function g(ζ)in C with respect to the spherical metric in P1,which further satisfies an estimateg♯(ζ)≤g♯(0)=1.Moreover,all zeros of g have multiplicity at least k and g has order at most 2.If g is holomorphic,then g is of exponential type and has order at most 1.
In Lemma 2.1,the order of g is de fined by using the Nevanlinna’s characteristic function T(r,g)of g:
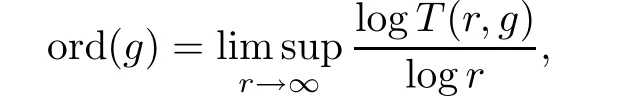
here g♯denotes the spherical derivative
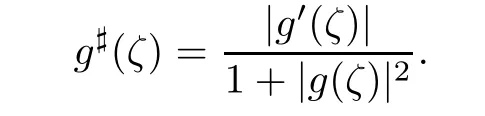
Lemma 2.2(see[3])Take a positive integer n.If f is a transcendental meromorphic function on C,then fnf′assumes every nonzero finite value in finitely often.
Lemma 2.3(see[1])Let ε be any positive number.If a Möbius transformation L satisfies estimates

for some constants a,b,c,then it also satisfies the following uniform Lipschitz’s condition
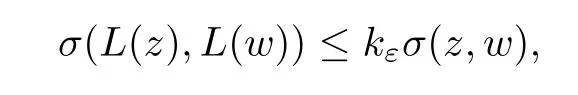
where kεis a constant depending on ε.
Lemma 2.4(see[4])Let p,q be co-prime polynomials,set deg(p)=n,deg(q)=m with m<n,and write R=q/p.If there is a positive integer k such that R(k)(z)0 for each z∈C,then m=0,and R assumes the following form

3 Proof of Theorem 1.1
Under conditions(ii),there exists nonzero constants b,c such thatis independent of f∈F,so that a Möbius transformation
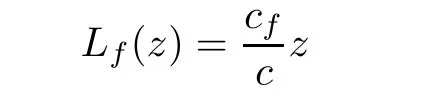
is associated to each f∈F withWe next show that the following family

associated to F is normal in D.
Suppose,to the contrary,that G is not normal in D,that is,there is at least a point z0∈D such that G is not normal at z0.By Lemma 2.1,there exist a sequence{zj}⊂D of complex numbers with zj→z0,a sequence{ρj}of positive numbers with ρj→0,and a sequencedetermined by a sequence{fj}⊂F such that
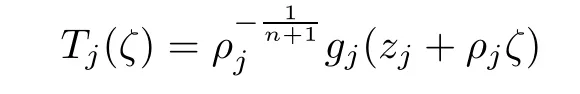
locally uniformly converge to a non-constant meromorphic function T(ζ)in C with respect to the spherical metric.Moreover,T is of order at most 2.Further,we claim
(A)TnT′−α has no zeros for α=cn+1;
(B)T′has no zeros.
To prove(A),suppose,to the contrary,that there exists a zero ζ0∈C of TnT′−α.
Noting that as j→∞,

it follows from Hurwitz’s theorem that there exists a sequence{ζj}of C converging to ζ0such that
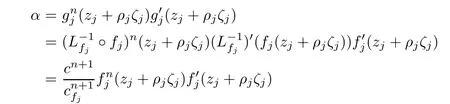
for large j,which yields
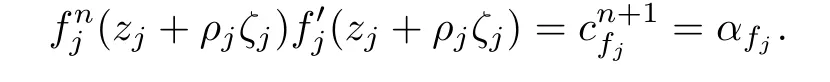
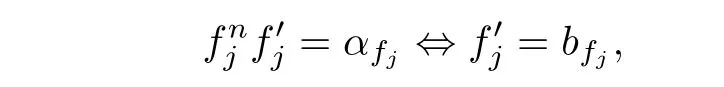
and hence we have

This contradicts with the assumption that Tn(ζ0)T′(ζ0)=α0.Therefore,claim(A)holds.
Next we con fi rm claim(B).Suppose,to the contrary,that there exists a ζ0∈C such that T′(ζ0)=0.Noting that
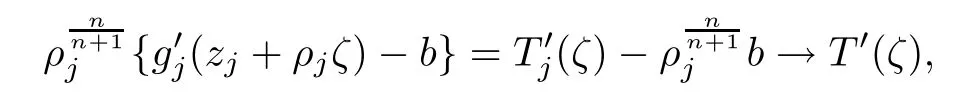
by Hurwitz’s theorem we can deduce that there exists a sequence{ζj}of C converging to ζ0such that
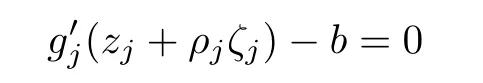
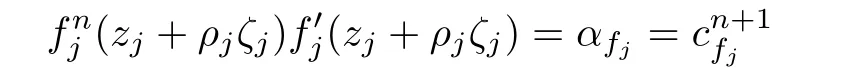
by the condition that fnf′=αf⇔f′=bf.Thus we obtain

This contradicts with claim(A).Hence claim(B)is true.
Therefore,it follows from Lemma 2.2 that the meromorphic function T is not transcendental since(A)holds,and hence T is rational.If T is a polynomial,then T must assume the form T(ζ)=c1(ζ−c2)for some constants c1(0),c2based on claim(B),which further implies that the function TnT′−α has zeros.This contradicts with claim(A).
If T is rational,but T is not a polynomial,then there exist polynomials p,q,r such that T assumes the form T=r+q/p,where p(0),q(0)are co-prime polynomials with deg(p)>deg(q).If r is not a constant,by differentiating T,we obtain a new form

where p1,q1are co-prime polynomials with deg(p1)>deg(q1),which obviously implies that T′has zeros.This contradicts with claim(B).
If r is constant,then(q/p)′=T′has no zeros,and hence it follows from Lemma 2.4 that

where d1(0),d2are constants,and m=deg(p)≥1.Thus,we easily find

and hence TnT′−α has zeros,which contradicts with claim(A).Therefore,the family G is normal in D,or equivalently G is equicontinuous at each point of D.
Note that condition(i)’yields
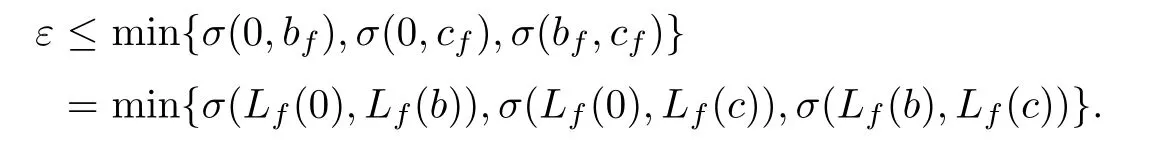
Hence Lemma 2.3 implies that Lfsatisfies the following uniform Lipschitz’s condition

where kεis a constant depending on ε.
Take a point z∈D.Since G is equicontinuous at z∈D,then for any∈>0,there existsδ>0 such that when w∈D satisfies σ(z,w)<δ,each f∈F satisfies an estimate
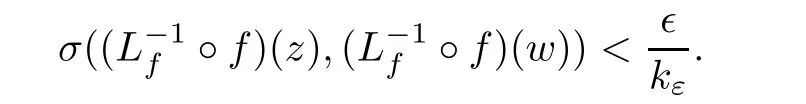
Hence when σ(z,w)<δ,each f∈F satisfies an estimate
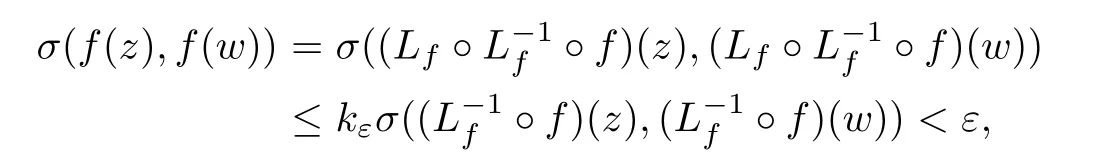
that is,the family F also is equicontinuous at z.Therefore F is normal in D.This completes the proof of Theorem 1.1.
4 Proof of Theorem 1.3
Under condition(ii)’,there exists nonzero constants a,b,c,β such thatare independent of f,respectively.Then we can also construct same family G determined by F similar to the proof of Theorem 1.1.Suppose,to the contrary,that the familyG is not normal in D,that is,there is at least a point z0∈D such that G is not normal at z0.By using Lemma 2.1,we also obtain the sequences{zj},{ρj},{fj},{gj},{Tj}and the non-constant meromorphic function T in C with same properties,and further propose claims(A)and(B).
In this case,the proof of claim(A)can be completed according to the arguments in the proof of Theorem 1.1.To prove(B),suppose,to the contrary,that there exists ζ0∈C such that T′(ζ0)=0.Noting that as j→∞
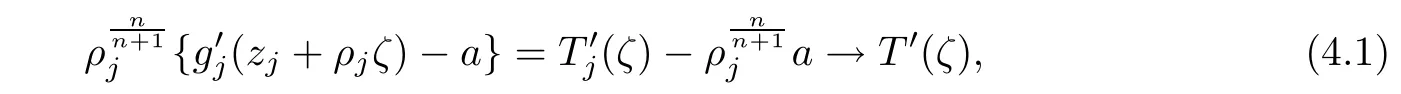
by Hurwitz’s theorem we can deduce that there exists a sequence{ζj}of C converging to ζ0such that
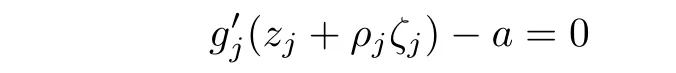
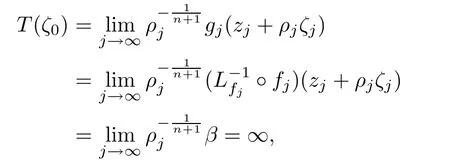
that is,ζ0is a pole of T.This is impossible since T′(ζ0)=0,and hence claim(B)is proved.
Then based on claims(A)and(B)and following arguments in the proof of Theorem 1.1,we can show that the family

is normal in D.
Note that condition(i)yields
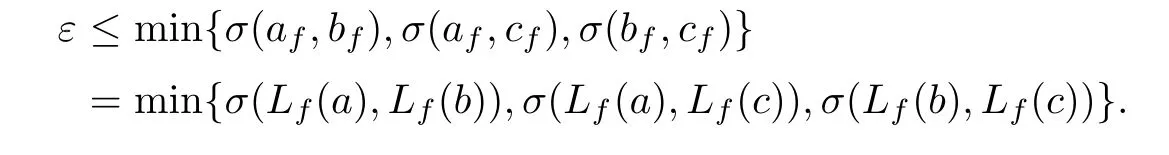
By Lemma 2.3,we can see that Lfsatisfies the following uniform Lipschitz’s condition
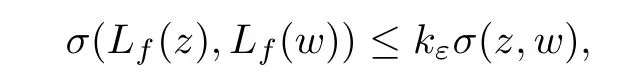
where kεis a constant depending on ε.
Take a point z∈D.Since G is equicontinuous at z∈D,then for any∈>0,there existsδ>0 such that when w∈D satisfies σ(z,w)<δ,each f∈F satisfies an estimate

Hence when σ(z,w)<δ,each f∈F satisfies an estimate

that is,the family F also is equicontinuous at z,and hence F is normal in D.This completes the proof of Theorem 1.3.
References
[1]Beardon A F.Iteration of Rational Functions.New York:Springer-Verlag,1991
[2]Carathéodory C.Theory of Functions of a Complex Variable,Vol II.New York:Chelsea Pul Co,1960
[3]Chen H H,Fang M L.On the distribution fnf′.Science in China,1995,38:121-127
[4]Fang M L,Yuan W J.On the normality for families of meromorphic functions.Indian J Math,2001,43(3):741-351
[5]Gu Y X.Normal Families of Meromorphic Functions.Chengdou:Sichuan Edu Press,1988(in Chinese)
[6]Grahl J,Nevo S.On a result of singh and singh concerning shared values and normality.Complex Var Theory Appl,2010,55:347-356
[7]Hayman W K.Research Problems of Function Theory.London:Athlone Press,1967
[8]Meng C.Normal Families and shared values of meromorphic functions.J Bull Math,2008,31(1):85-90
[9]Pang X C.On normal criterion of meromorphic functions.Sci China Ser A,1990,33:521-527
[10]Pang X C,Zalcman L.Normal families and shared values.Bull London Math Soc,2000,32:325-331
[11]Pang X C,Zalcman L.Normality and shared values.Ark Mat,2000,38:171-182
[12]Schi ff J.Normal Families.Berlin:Springer-Verlag,1993
[13]Singh A P,Singh A.Sharing values and normality of meromorphic fuctions.Complex Var Theory Appl,2004,49(6):417-425
[14]Zalcman L.Normal families:New perspectives.Bull Amer Math Soc,1998,35:215-230
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- SOME STABILITY RESULTS FOR TIMOSHENKO SYSTEMS WITH COOPERATIVE FRICTIONAL AND INFINITE-MEMORY DAMPINGS IN THE DISPLACEMENT∗
- STABILITY OF VISCOUS SHOCK WAVES FOR THE ONE-DIMENSIONAL COMPRESSIBLE NAVIER-STOKES E QUATIONS WITH DENSITY-DEPENDENT VISCOSITY∗
- STABILITY ANALYSIS OF A COMPUTER VIRUS PROPAGATION MODEL WITH ANTIDOTE IN VULNERABLE SYSTEM∗
- STABILITY OF A PREDATOR-PREY SYSTEM WITH PREY TAXIS IN A GENERAL CLASS OF FUNCTIONAL RESPONSES∗
- NONSMOOTH CRITICAL POINT THEOREMS AND ITS APPLICATIONS TO QUASILINEAR SCHRÖDINGER EQUATIONS∗
- EDELSTEIN-SUZUKI-TYPE RESULTS FOR SELF-MAPPINGS IN VARIOUS ABSTRACT SPACES WITH APPLICATION TO FUNCTIONAL EQUATIONS∗
