ZERO DISSIPATION LIMIT TO CONTACT DISCONTINUITY FOR THE COMPRESSIBLE NAVIER-STOKES SYSTEM OF GENERAL GAS∗
2016-04-18HakhoHONGInstituteofMathematicsAcademyofSciencesKorea
Hakho HONGInstitute of Mathematics,Academy of Sciences,D.P.R.Korea
ZERO DISSIPATION LIMIT TO CONTACT DISCONTINUITY FOR THE COMPRESSIBLE NAVIER-STOKES SYSTEM OF GENERAL GAS∗
Hakho HONG
Institute of Mathematics,Academy of Sciences,D.P.R.Korea
E-mail:hhong@amss.ac.cn
AbstractThe zero dissipation limit to the contact discontinuities for one-dimensional compressible Navier-Stokes equations was recently proved for ideal polytropic gas(see Huang et al.[15,22]and Ma[31]),but there is few result for general gases including ideal polytropic gas.We prove that if the solution to the corresponding Euler system of general gas satisfying(1.4)is piecewise constant with a contact discontinuity,then there exist smooth solutions to Navier-Stokes equations which converge to the inviscid solutions at a rate of κ14as the heat-conductivity coeffi cient κ tends to zero.The key is to construct a viscous contact wave of general gas suitable to our proof(see Section 2).Notice that we have no need to restrict the strength of the contact discontinuity to be small.
Key wordszero dissipation limit;Navier-Stokes equations;contact discontinuity;general gas
2010 MR Subject Classi fi cation76N99;35Q30;35L65;74J40
∗Received October 20,2014;revised July 4,2015.
1 Introduction
The one-dimensional compressible Navier-Stokes equations in Lagrangian coordinates are expressed as

where x∈R1=(−∞,∞),t>0,v(x,t)>0,u(x,t),e(x,t)>0,θ(x,t)>0 and p(x,t)are the speci fi c volume,the velocity,the internal energy,the temperature and the pressure,respectively,whileµand κ denote the viscosity and the heat-conductivity coeffi cients respectively.We assume,as usual in thermodynamics,that by using any given two of the fi ve thermodynamical variables(v,p,e,θ and s),the remaining three variables are smooth functions of them,where s is the entropy of the gas.

The second law of thermodynamics asserts that from which,if we choose(v,θ)or(v,s)as independent variables and write(p,e,s)=(p(v,θ),respectively,then we can deduce that

or
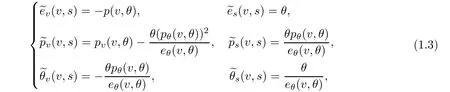
Throughout this paper,the pressure p(v,θ)and the internal energy e(v,θ)are assumed to satisfy

From(1.3)and(1.4)we have

The study of the vanishing viscosity limit of viscous flows is an important problem in the theory of the compressible fluids flows.In the case ofµ=κ=0,the system(1.1)becomes the inviscid Euler system
which is one of the most important nonlinear strictly hyperbolic systems of conservation laws.Since the inviscid system(1.7)is an idealization when the dissipative effects are neglected,it is expected that general weak entropy solutions to the Euler equations should be the limit of solutions to the corresponding Navier-Stokes equations as viscosity and heat conductivity tend to zero.When the solution of the inviscid system is smooth,the zero dissipation limit can beinvestigated through classical scaling method.However,the solutions to the inviscid system(1.7)are,in general,discontinuous like shock and contact wave and their investigation is more complicated.

Indeed,there were great interest and intensive studies on the vanishing viscosity limit of viscous flows.For the case that the solution to the Euler system(1.7)consists of a single shock wave,Ho ff-Liu[13]first investigated the zero dissipation limit for isentropic Navier-Stokes equations and they proved that the solution of the isentropic Navier-Stokes equations with shock data exists and converges to the shock wave solution of the corresponding isentropic Euler equations as the viscosity goes to zero.On the other hand,for the hyperbolic conservation laws with arti fi cial viscosity

Goodman-Xin[11]proposed a matched asymptotic expansion method to study the zero dissipation limit in the presence of shock wave.Later,several authors revealed the rich structure of vanishing viscosity limit of shock waves for the full Navier-Stokes equations and more general viscous conservation laws(see[36,38,43]).As far as rarefaction wave is concerned,Xin in[39]proved that the solution to the isentropic Navier-Stokes equations with weak centered rarefaction wave data exists for all the time and converges to the weak centered rarefaction wave solution of the corresponding Euler equations as viscosity tends to zero.Later,Jiang-Ni-Sun[26]and Xin-Zeng[42]generalized the results of[39]to the full Navier-Stokes equations,provided that the viscosity and heat conductivity are in the same order.Huang and Li in 2012 improved the convergence rate of[39]for the isentropic Navier-Stokes equations.
However,in the case that the solutions to the Euler equations containing contact discontinuity,zero dissipation limit is much more subtle due to various difficulty.Recently,in the case of ideal polytropic gas,Ma[31],Huang-Wang-Yang[22]and Huang-Jiang-Wang[15]proved the zero dissipation limit toward contact discontinuity for the compressible Navier-Stokes equations.Moreover,Huang-Wang-Yang[22]and Huang-Jiang-Wang[15]showed the zero dissipation limit to the superposition of two rarefaction waves and contact discontinuity for compressible Navier-Stokes equations,but there is few result for the zero dissipation limit toward contact discontinuity in the case of general gases including ideal polytropic gas which is the target of this paper.The precise statement of our result will be found in Theorem 2.5 of next section.
Just recently,Huang-Wang-Yang in[23]proved the vanishing viscosity limit to the superposition of shock and rarefaction waves for compressible Navier-Stokes equations.
Recently,Chen-Perepelitsa[4]proved the convergence of the isentropic compressible Navier-Stokes equations to the compressible Euler equations as the viscosity vanishes in Eulerian coordinates for general initial data by using compensated compactness method if the far field does not contain vacuum.Note that this result allows the initial data containing vacuum in the interior domain.However,the framework of compensated compactness is basically limited to 2×2 systems so far,so that this result could not be applied to the full compressible Navier-Stokes equations
We also mention that there are a lot of extensive literature on the vanishing arti fi cial viscosity limit for hyperbolic systems of conservation laws(see,for example,[2,3,6,7,12,28,29,34,40,41]and the references therein).For the stability of wave pattern of viscousconservation laws,see the reference[10,18,19,25,30,32,33,35]and therein.
NotationThroughout the rest of this paper,O(1),c or C will be used to denote a generic positive constant independent of t and x and ci(·,·)or Ci(·,·)(i∈Z+)stands for some generic constants depending only on the quantities listed in the parentheses.As long as no confusion arises,denotes the usual Sobolev space with norm‖·‖Hkby Hk:=Hk(R1)and‖·‖H0=‖·‖will be used to denote the usual L2-norm.Finally,‖·‖Lpand·dx are used to denote‖·‖Lp(R1)andR1·dx,respectively.
2 Viscous Contact Wave and Main Theorem
We first construct a viscous contact wave(V,U,Θ)for the compressible Navier-Stokes equations(1.1)in the case of general gases satisfying(1.4).
By using(1.2),we can rewrite(1.1)3as the equations for the entropy s and the temperature θ
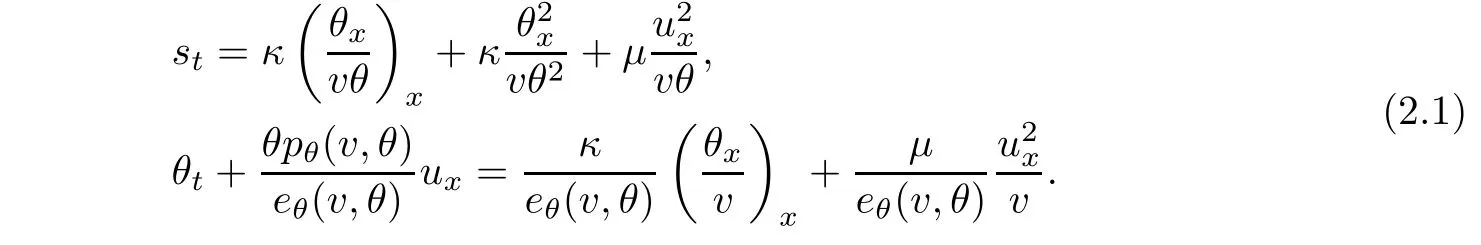
It is well known that the Riemann problem to the corresponding Euler system(1.7)with the Riemann initial data

admits a contact discontinuity

provided that

Motivated by(2.3),we expect

Since pv(v,θ)<0,the implicit function theorem implies that there exists a smooth function f(Θ)such that

in a small neighborhood N of Θ(see[24]).From(2.4)and(2.5),we have
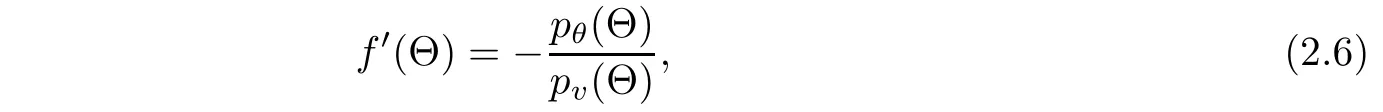
where pθ(Θ)=pθ(f(Θ),Θ)and pv(Θ)=pv(f(Θ),Θ).By(2.4),(1.1)1and(2.1)2,we can conjecture that(V,U,Θ)satisfies

where eθ(Θ)=eθ(f(Θ),Θ)>0.
Having in mind(2.5)-(2.7),we consider a nonlinear di ff usion equation
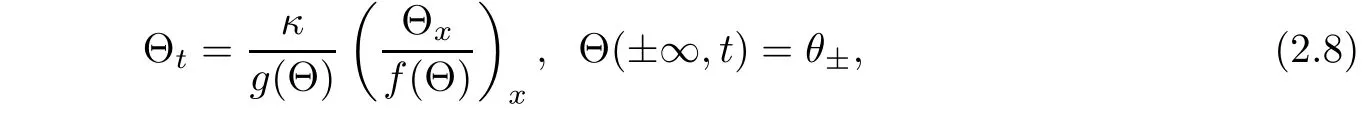
Lemma 2.1Under assumptions(2.3)and(1.4),there is a smooth unique self-similarity solutionof problem(2.8)satisfying the following properties:on one hand,is a monotone function,increasing if θ+>θ−and decreasing if θ−>θ+;on the other hand,satisfies

ProofBy(2.8)and
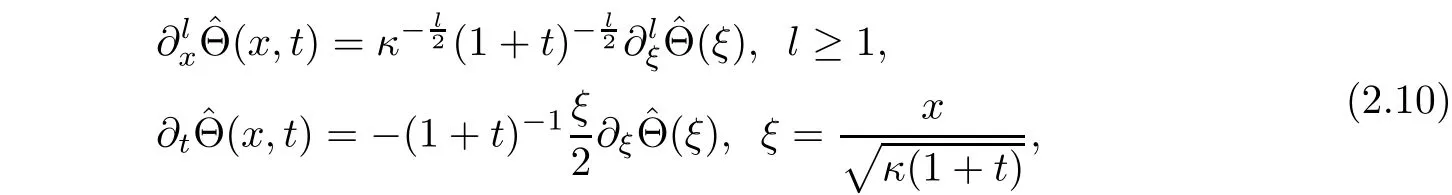
ˆΘ(ξ),ξ∈(−∞,∞)satis fies the boundary value problem of the following ordinary differential equation
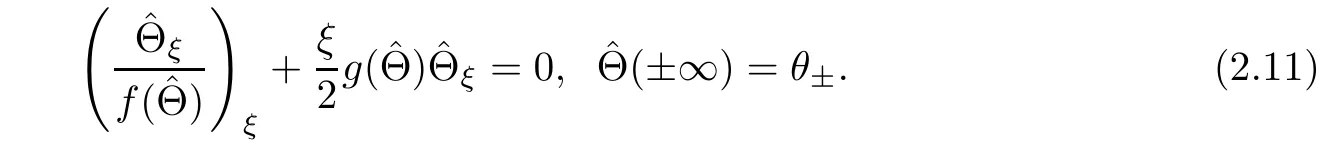


By the same method in[1,9],system(2.12)admits a unique self-similarity solutionsatisfying the following properties:on one hand,is a monotone function,increasing ifand decreasing ifon the other hand,Θ satisfies


where
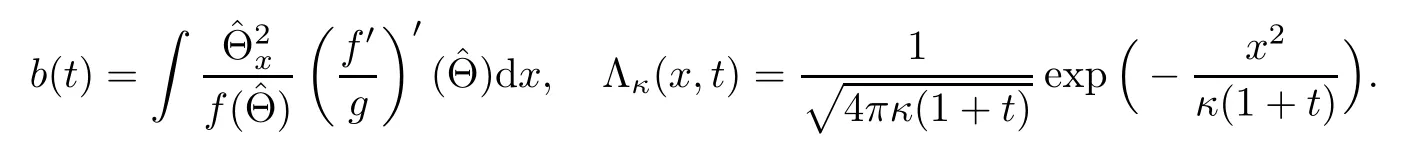
Note thatΛκ(x,t)dx=1 and(V,U,Θ)(±∞,t)=(v±,u±,θ±).
Remark 2.2For ideal polytropic gas,the pressure p and the internal energy e are given by

where R>0 is the gas constant and γ>1 is the adiabatic exponent.Therefore,the function f in(2.5)and g in(2.8)are
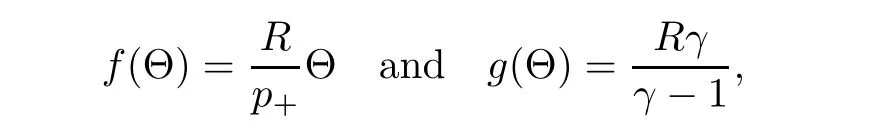
respectively.This implies thatand(2.14)becomes
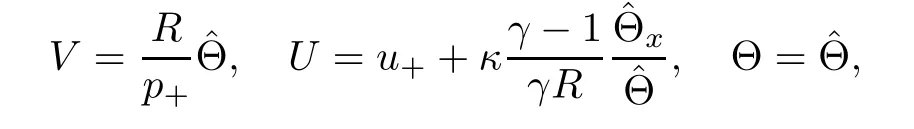
which means the viscous contact wave in the case of ideal polytropic gas,whereis a unique self-similarity solution to the nonlinear di ff usion equation
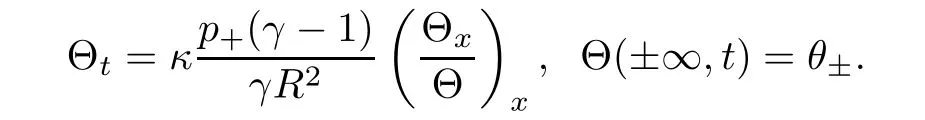
It is easy to check the following lemma.
Lemma 2.3Under assumptions(2.3)and(1.4),the viscous contact wave(V,U,Θ)de fined by(2.14)satisfies

and

where
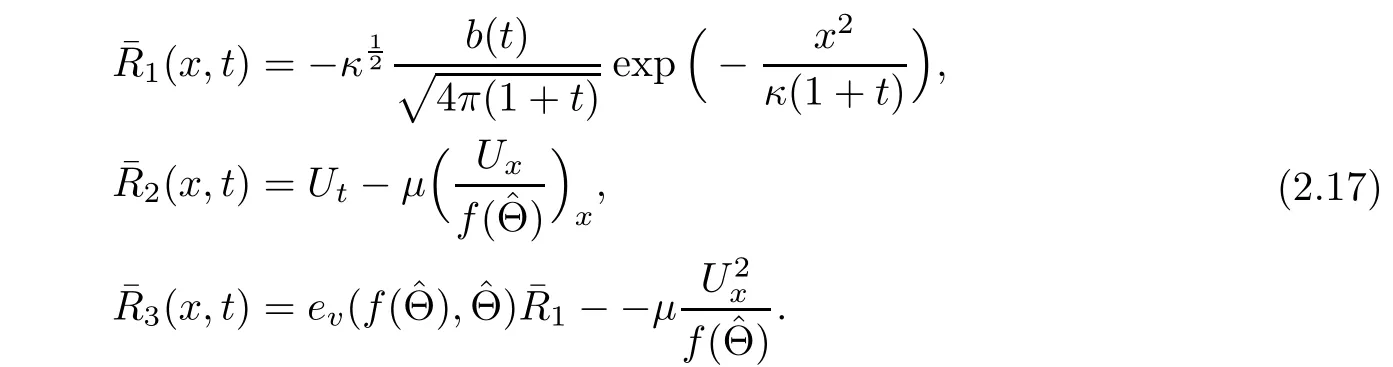
For a given positive constant κ0,we set

where c is a positive constant.
Then our result can be stated as follows:

Then,for any arbitrary large T>0,there exist a small positive constant κ0such that for eachκ∈∆(κ0),the compressible Navier-Stokes equations(1.1)with initial data

admit a unique global solution(v,u,θ)satisfying

and for any h>0,
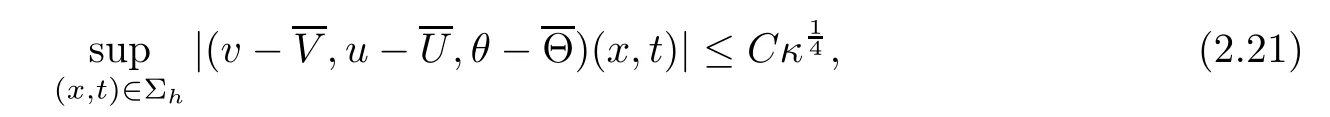
3 Reformulation of the Problem
Instead of equation(2.16)3,it is convenient to work with the equations for the entropy s(V,Θ)and the temperature Θ
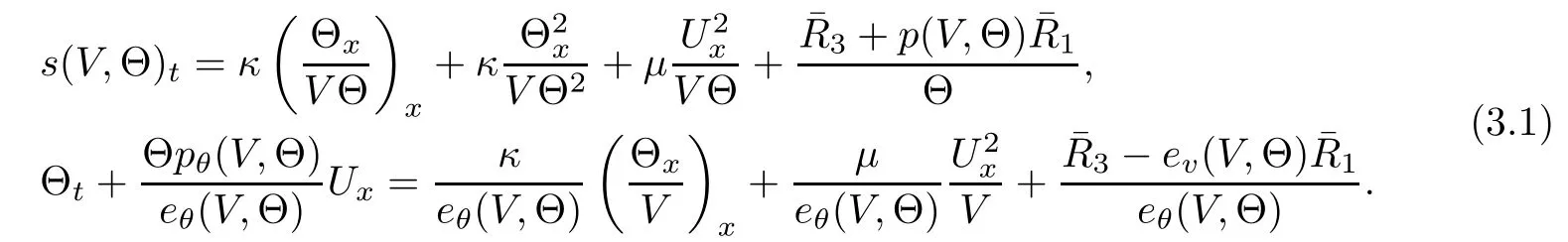
We rewrite the Cauchy problem(1.1)1,(1.1)2,(2.1)2and(2.20)by the following scalings
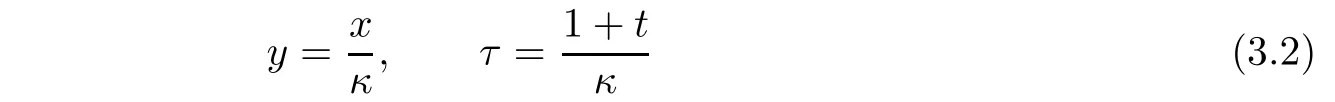
to obtain

with initial data

where∈=µ/κ,τ0=κ−1and by virtue of(2.18),
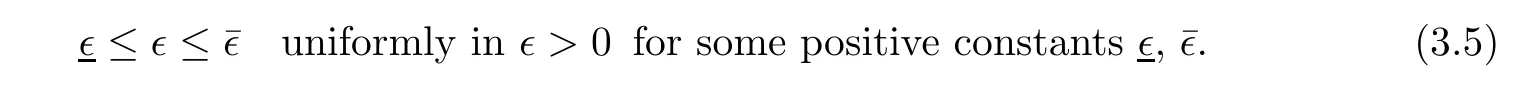
Also,we rewrite(2.16)1,(2.16)2,(3.1)2by scalings(3.2)to obtain
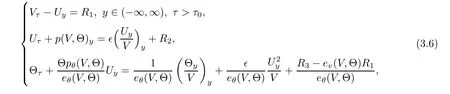
By(2.17)and(3.2),

where

By(3.8),(2.9)and

we have
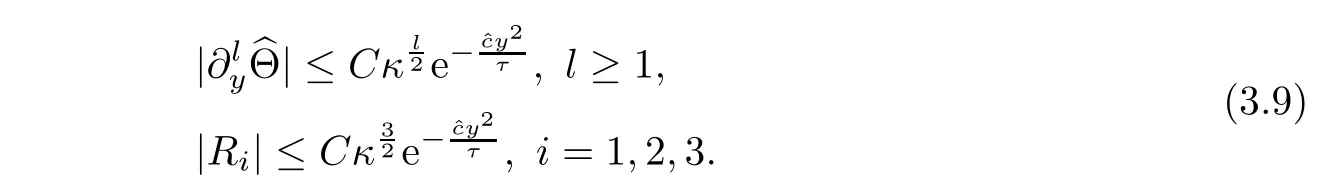
Setting
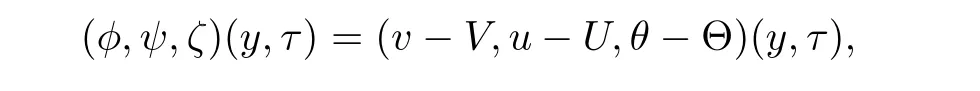
we obtain from(3.3),(3.6)and(3.4)

and

For any interval I⊂[0,∞),we de fi ne a function space X(I)as
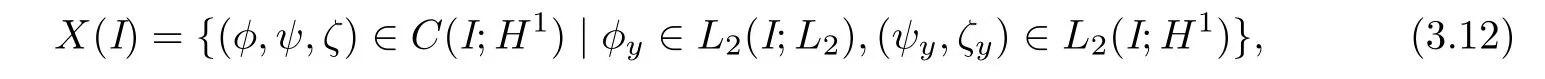
then we state the local existence of the solution to the Cauchy problem(3.10),(3.11)(see Lemma 3.1 in[8]).
Proposition 3.1Assume that the initial data(v0,u0,θ0)satisfy

Then,the Cauchy problem(3.10),(3.11)admits a unique solution(φ,ψ,ζ)∈X([τ0,τ1])for some sufficiently small τ1>τ0and(φ,ψ,ζ)(y,τ)satisfies

for all τ0≤τ≤τ1,where ϕ=s(v,θ)−s(V,Θ)andare positive constants independent of y.Here τ1depends only on‖(φ,ψ,ζ)(τ0)‖H1.
To prove Theorem 2.5,a crucial step is to show the following a priori estimate.
Proposition 3.2(A priori estimates)For τ0<τ1<∞,let(φ,ψ,ζ)∈X([τ0,τ1])be the solution to the Cauchy problem(3.10),(3.11)and assume that(2.19)and

where ε0is a small positive constant.Then,there exist positive constants κ0and C,which is independent of τ1,such that if κ∈∆(κ0),then the following estimates hold;

for all τ∈[τ0,τ1].
Proposition 3.2 is an easy consequence of Lemmas 4.1-4.2 in next section.
4 A Priori Estimates
Lemma 4.1Under the assumption of Proposition 3.2,the following estimate holds

for all τ∈[τ0,τ1],where C is the positive constant independent of τ1,κ.
ProofLet

where S=s(V,Θ),then by(1.1),(2.1),(2.16)and(3.1),we have

Noticing that

and by(1.3),

we drive from(4.3)that

where

where ϕ=s−S.
Cauchy inequality yields
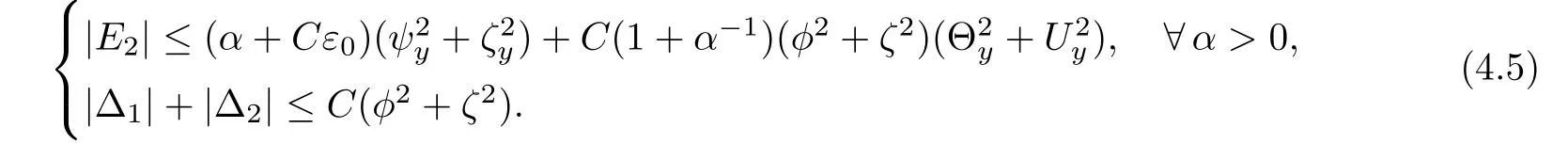
On the other hand,we get from(3.9)
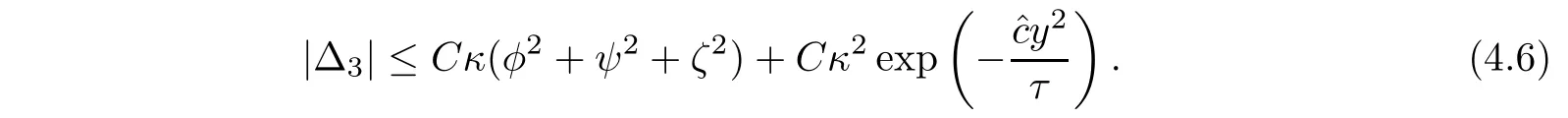
Notice that from(1.3)and(1.6),

Therefore,integrating(4.4)and using(4.5)-(4.7),we have
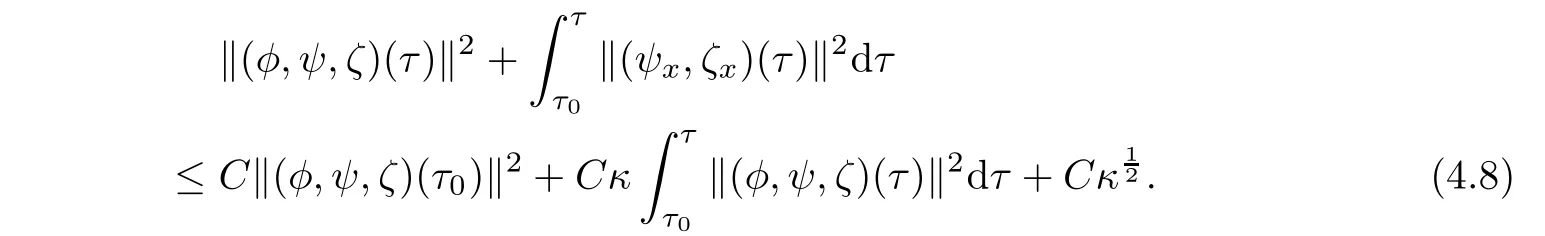
By(2.19),we get

Applying Gronwall’s inequality to(4.8)and using(4.9),we obtain(4.1)which fi nishes the proof of lemma.
Lemma 4.2Under the assumption of Proposition 3.2,it follows that
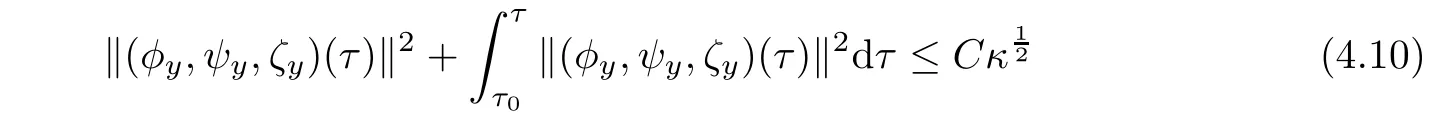
for all τ∈[τ0,τ1],where C ia the positive constant independent of τ1,κ.
ProofRewriting(3.10)2as

and multiplying(4.11)by φx/v,we have
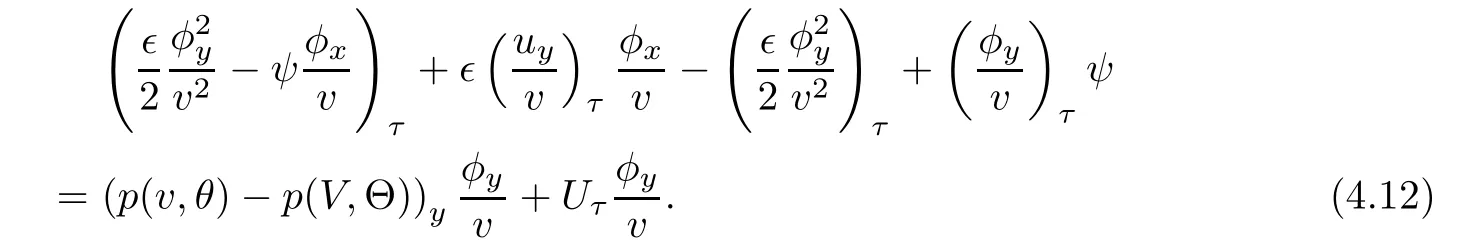
Using
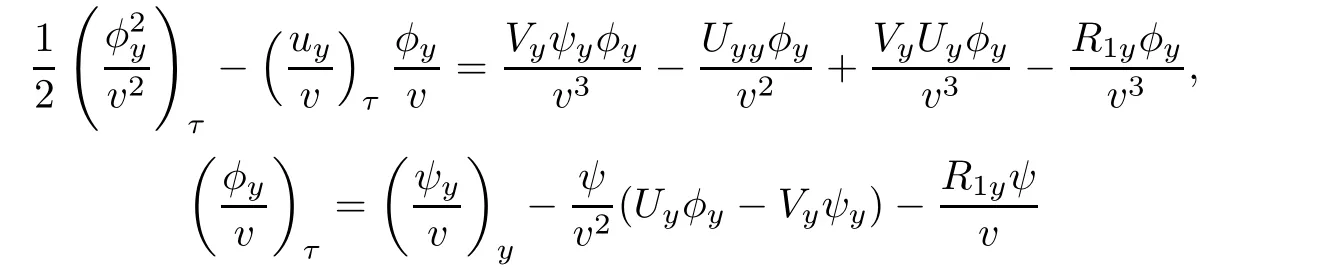
and

we rewrite(4.12)as

Integrating(4.12)with respect to(y,τ)and using(1.4),(3.5)and Cauchy inequality yields

Using(3.9)and(3.5),we estimate Ii,i=1,···,3 as follows:
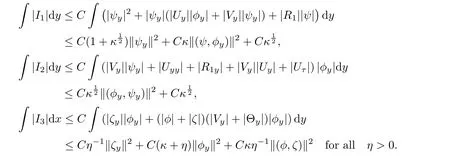
By(2.19),we get

Using estimates Ii,i=1,···,3,(4.1),(4.9)and(4.15),we obtain from(4.14)
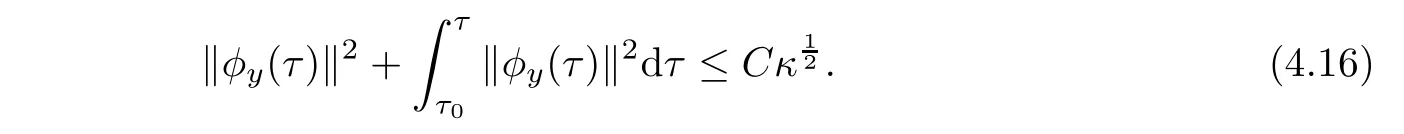
Rewrite(3.10)2as
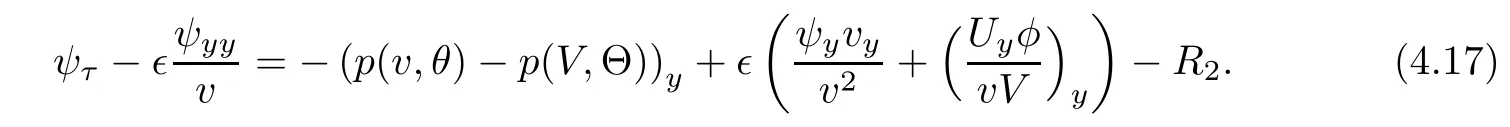
Multiplying(4.17)by−ψyyand integrating the resulting system with respect to(y,τ),we have
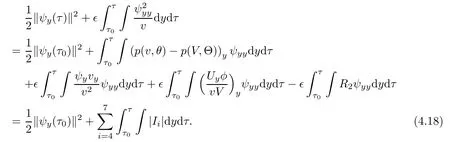
Using(3.9)and(3.5),we estimate Ii,i=4,···,7 as follows:
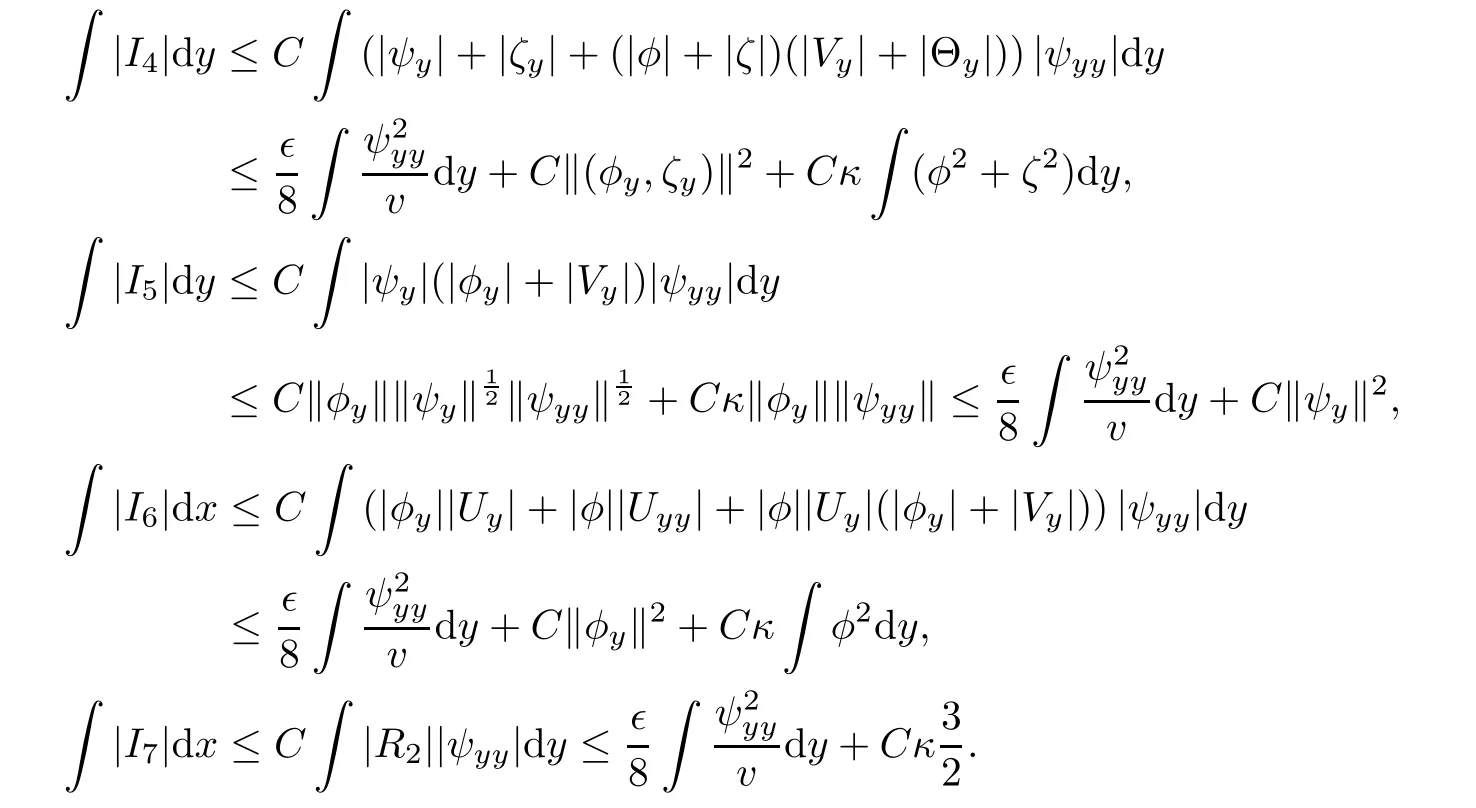
Using estimates Ii,i=4,···,7,(4.1),(4.15)and(4.16),we obtain from(4.18)
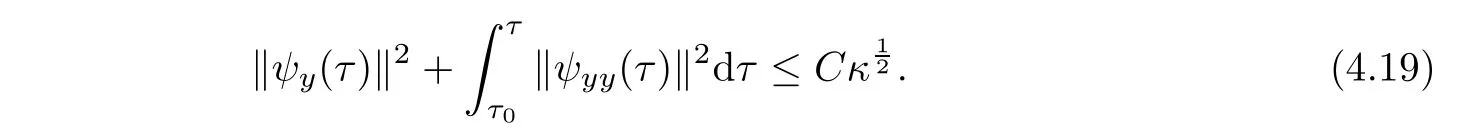
Multiplying(3.10)3by−ζyyand integrating the resulting system with respect to(y,τ),we have


where we used
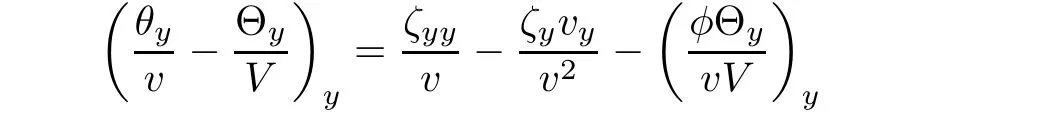
and
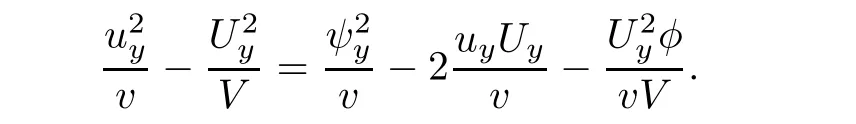
By(1.4)and(4.20),we have

Using(3.9).(1.4)and(3.5),we estimate Ii,i=4,···,7 as follows:

Using estimates Ii,i=4,···,7,(4.1),(4.15),(4.16)and(4.19),we obtain from(4.21)

By(4.16),(4.19)and(4.22),we obtain(4.10).This completes the proof of lemma.
5 The Proof of Main Result
Combining the results of Propositions 3.1 and 3.2 leads to
Proposition 5.1Under the assumption of Theorem 2.5,for any arbitrary large T>0,there exist a small positive constant κ0such that for each κ∈∆(κ0),the Cauchy problem(3.3),(3.4)admits a unique global solutionand the following estimate holds

where C is positive constant independent of κ.

By using Lemma 2.1,we get for any h>0,whereand C is positive constant depend on κ0,T,h and independent of κ.
By(5.1)and(5.2),we obtain(2.21).Hence we have completed the proof of Theorem 2.5.
References
[1]Atkinson F V,Peletier L A.Similariry solutions of the nonlinear di ff usion equation.Arch Ration Mech Anal,1974,54:373-392
[2]Bianchini S,Bressan A.Vanishing viscosity solutons of nonlinear hyperbolic systems.Ann Math,2005,161:223-342
[3]Bressan S,Yang T.On the convergence rate of vanishing viscosity approximations.Comm Pure Appl Math,2004,57:1075-1109
[4]Chen G Q,Perepelista M.Vanishing viscosity limit of the Navier-Stokes equations to the Euler equations for compressible fl uid fl ow.Commun Pure Appl Math,2010,63:1469-1504
[5]Courant R,Friedrichs K O.Supersonic Flow and Shock Waves.5th ed.Springer-Verlag,1999
[6]DiPerna R J.Convergence of approximate solutions to conservation laws.Arch Rat Mech Anal,1983,83:27-70
[7]DiPerna R J.Convergence of the viscosity method for isentropic gas dynamics.Comm Math Phys,1983,91:1-30
[8]Duan R,Liu H X.Zhao H J.Nonlinear stability of rarefaction waves for the compressible Navier-Stokes equations with large initial perturbation.Trans American Math Soc,2009,361(1):453-493
[9]Duyn C T,Peletier L A.A class of similariry solution of the nonlinear di ff usion equation.Nonlinear Anal,1977,1:223-233
[10]Goodman J.Nonlinear asymptotic stability of viscous shock profiles for conservation laws.Arch Ration Mech Anal,1986,95(4):325-344
[11]Goodman J,Xin Z P.Viscous limits for piecewise smooth solutions to systems of conservation laws.Arch Ration Mech Anal,1992,121(3):235-265
[12]Guès O,Métivier G,Williams M,Zumbrun K.Existence and stability of multidimensional shock fronts in the vanishing viscosity limit.Arch Ration Mech Anal,2005,175(2):151-144
[13]Ho ff D,Liu T P.The inviscid limit for the Navier-Stokes equations of compressible isentropic fl ow with shock data.Indiana Univ Math J,1989,36(4):861-915
[14]Ho ff D,Liu T P.Nonlinear di ff usive phenomena of nonlinear hyperbolic systems.Chin Ann Math,1993,14B(4):235-265
[15]Huang F M,Jiang S,Wang Y.Zero dissipation limit of full compressible Navier-Stokes equations with a Riemann initial data.Commun Inform Sys,2013,13(2):211-246
[16]Huang F M,Li M J,Wang Y.Zero dissipation limit to rarefaction wave with vacuum for 1-D compressible Navier-Stokes equations.SIAM J Math Anal,2012,44(3):1742-1759
[17]Huang F M,Li X.Zero dissipation limit to rarefaction waves for the 1-D compressible Navier-Stokes equations.Chin Ann Math Ser B,2012,33(3):385-394
[18]Huang F M,Matsumura A,Xin Z P.Stability of contact discontinuities for the 1-D compressible Navier-Stokes equations.Arch Ration Mech Anal,2005,179:55-77
[19]Huang F M,Wang Y,Wang Y,Yang T.The limit of the Boltzmann equation to the Euler equations for Riemann problems.SIAM J Math Anal,2013,45:1741-1811
[20]Huang F M,Wang Y,Wang Y,Yang T.Vanishing viscosity of isentropic Navier-Stokes equations for interacting shocks.Sci China Math,2015,58(4):653-672
[21]Huang F M,Wang Y,Yang T.Hydrodynamic limit of the Boltzmann equation with contact discontinuities.Comm Math Phys,2010,295(2):293-326
[22]Huang F M,Wang Y,Yang T.Fluid dynamic limit to the Riemann solutions of Euler equations:I.superposition of rarefaction waves and contact discontinuity.Kinet Related Models,2010,3:685-728
[23]Huang F M,Wang Y,Yang T.Vanishing viscosity limit of compressible Navier-Stokes equations for solutions to a Riemann problem.Arch Ration Mech Anal,2012,203:379-413
[24]Huang F M,Wang Y,Zhai X Y.Stability of viscous contact wave for compressible Navier-Stokes system of general gas with free boundary.Acta Math Sci,2010,30B(6):1906-1916
[25]Huang F M,Xin Z P,Yang T.Contact discontinuity with general perturbations for gas motions.Adv Math,2008,219(4):1246-1297
[26]Jiang S,Ni G X,Sun W J.Vanishing viscosity linit to rarefaction waves for the Navier-Stokes equations of dne-dimensional compressible heat-conducting fluids.SIAM J Math Anal,2006,38(2):368-384
[27]Li M J,Wang T,Wang Y.The limit to rarefaction wave with vacuum for 1D compressible fluids with temperature-dependent viscosities.Anal Appl,2015,13(5):555-589
[28]Lions P L,Perthame B,Souganidis P E.Existence and stability of entrophy solutions for the hyperbolic systems of isentropic gas dynamics in Eulerian and Lagrangian coordinates.Comm Pure Appl Math,1996,49:599-638
[29]Lions P L,Perthame B,Tadmor E.Kinetic formulation of sentropic gas dynamics and p-system.Comm Math Phys,1994,163:415-431
[30]Liu T P.Nonlinear stability of shock waves for viscous conservation laws.Mem Amer Math Soc,1985,56(329):1-108
[31]Ma S X.Zero dissipation limit to strong contact discontinuity for the 1-D compressible Navier-Stokes equations.J Di ff Equs,2010,248:95-110
[32]Matsumura A,Nishihara K.On the stability of travelling wave solutions of a one-dimensional model system for compressible viscous gas.Jpn J Appl Math,1985,2:17-25
[33]Matsumura A,Nishihara K.Asymptotics toward the rarefaction wave of the solutions of a one-dimensional model system for compressible viscous gas.Jpn J Appl Math,1986,3:1-13
[34]Serre D,Zumbrun K.Boundary layer stability in real vanishing viscosity limit.Comm Math Phys,2001,221:267-292
[35]Szepessy A,Xin Z P.Nonlinear stability of viscous shock waves.Arch Ration Mech Anal,1993,122:53-103
[36]Wang H Y.Viscous limits for piecewise smooth solutions for the p-system.J Math Anal Appl,2004,299:411-432
[37]Wang T.Vanishing viscosity limit to rarefaction wave with vacuum for 1-D compressible Navier-Stokes equations with density-dependent viscosity.Commun Math Sci,2015,13(2):477-495
[38]Wang Y.Zero dissipation limit of the compressible heat-conducting Navier-Stokes equations in the presence of the shock.Acta Math Sci,2008,28B(4):727-748
[39]Xin Z P.Zero dissipation limit to rarefaction waves for the dne-dimensinal Navier-Stokes equations of compressible isentropic gases.Comm Pure Appl Math,1993,46:621-665
[40]Xin Z P.Viscous boundary layers and their stability.1.J Partial Di ff Equs,1998,11:97-124
[41]Xin Z P,Yanagisawa T.Zero-viscosity limit of the linearized Navier-Stokes equations for a compressible viscous fl uid in the half-plane.Comm Pure Appl Math,1999,52:497-541
[42]Xin Z P,Zeng H.Convergence to rarefaction waves for nonlinear Boltzmann equation and compressible Navier-Stokes equations.J Di ff er Equ,2010,249:827-871
[43]Yu S H.Zero dissipation limit of solutions with shocks for systems of hyperboloc conservation laws.Arch Ration Mech Anal,1999,146(4):275-370
[44]Zhang Y H,Pan R H,Wang Y,Tan Z.Zero dissipation limit with two interacting shocks of the 1D non-isentropic Navier-Stokes equations.Indiana Univ Math J,2013,62(1):249-309
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- SOME STABILITY RESULTS FOR TIMOSHENKO SYSTEMS WITH COOPERATIVE FRICTIONAL AND INFINITE-MEMORY DAMPINGS IN THE DISPLACEMENT∗
- STABILITY OF VISCOUS SHOCK WAVES FOR THE ONE-DIMENSIONAL COMPRESSIBLE NAVIER-STOKES E QUATIONS WITH DENSITY-DEPENDENT VISCOSITY∗
- STABILITY ANALYSIS OF A COMPUTER VIRUS PROPAGATION MODEL WITH ANTIDOTE IN VULNERABLE SYSTEM∗
- STABILITY OF A PREDATOR-PREY SYSTEM WITH PREY TAXIS IN A GENERAL CLASS OF FUNCTIONAL RESPONSES∗
- NONSMOOTH CRITICAL POINT THEOREMS AND ITS APPLICATIONS TO QUASILINEAR SCHRÖDINGER EQUATIONS∗
- NORMAL FAMILIES OF MEROMORPHIC FUNCTIONS WITH SHARED VALUES∗
