HURWITZ-HODGE INTEGRAL IDENTITIES FROM THE ORBIFOLD MARIÑO-VAFA FORMULA∗
2016-04-18ChenZHAO赵晨SchoolofMathematicalSciencesCenterofMathematicalSciencesZhejiangUniversityHangzhou310027China
Chen ZHAO(赵晨)School of Mathematical Sciences;Center of Mathematical Sciences,Zhejiang University,Hangzhou 310027,China
HURWITZ-HODGE INTEGRAL IDENTITIES FROM THE ORBIFOLD MARIÑO-VAFA FORMULA∗
Chen ZHAO(赵晨)
School of Mathematical Sciences;Center of Mathematical Sciences,Zhejiang University,Hangzhou 310027,China
E-mail:lancyzhao@gmail.com
AbstractIn this paper,we present some polynomial identities of Hurwitz-Hodge integral.Subsequently,we present how to obtain some Hurwitz-Hodge integral identities from the polynomial identity.Lastly,we give a recursion formula for Hurwitz-Hodge integral〈τbLλgλ1〉ag.
Key wordsHurwitz-Hodge integral;orbifold Mariño-Vafa formula;polynomial identities; recursion formula
2010 MR Subject Classi fi cation81Q30;81T30
∗Received October 21,2014;revised May 14,2015.
1 Introduction
Let X be a proper smooth Deligne-Mumford stack with a projective coarse moduli space X,and let β be an effective curve class in X.Denotebe the moduli stack of n-pointed,genus g,degree β twisted stable maps to X.Thenis a proper Deligne-Mumford stack.The Gromov-Witten invariants on the stack(orbifold)X are the intersection numbers onFor each marking i,there is an associated cotangent line bundle Liwith fi berThe intersection numbers of the chern classes of these line bundles onare related to the classical Hurwitz numbers[14].
Orbifold string theory became an important part of the landscape of string theory since the work of Dixon,Harvey,Vafa and Witten[8,9].The Gromov-Witten theory for symplectic orbifolds was developed by Chen-Ruan[7].Later,Abramovich,Graber,Vistoli established the Gromov-Witten theory for smooth Deligne-Mumford stacks[1].By the virtual localization,the computation of orbifold Gromov-Witten invariants for a toric DM stack reduced to the computation of the Hurwitz-Hodge integrals on the moduli spaceof twisted stable maps to the classifying stack of a finite group G[16].Bryan,Graber and Pandharipande pursued a systematic approach to the orbifold Gromov-Witten theory of Gorenstein stacks via Hurwitz-Hodge integrals in their works[2]and[3],inspired by Costello’s[6].In[3],through the explicit evaluation of λg−1on moduli spaces of admissible Z3-covers,they also described the Gromov-Witten potential of the quotient stack[Z2/Z3]and showed that the Crepant Resolution Conjecture is veri fied in that case.After that,Cavalieri gives descendants nice combinatorial structures of the Hurwitz-Hodge integrals in[4].In[20],Zhou described an effective algorithm tocalculate the Hurwitz-Hodge integrals.By applying Tseng’s orbifold quantum Riemann-Roch theorem[18],Hurwitz-Hodge integrals can be reconstructed from the descendant Hurwitz-Hodge integrals on the moduli spacesof twisted stable maps to the classifying stack of a finite group G:

Jarvis-Kimura related the descendant integrals on
Given a character


Some closed formulas of the Hurwitz-Hodge integrals relatingwere given in[13].
In this paper,we deduce the following λgformula.
Theorem 1.1When bi≥0 for 1≥i≥l,andwe have

Denote the forgetful map

Notice that E1=π∗E where E is the Hodge bundle onBy the projection formula,Theorem 1.1 is equivalent to the classical λg-conjecture which was first proved in[11].In this paper,we give another proof based on the Laplace transform of the orbifold cut-and-join equation in[22],which was deduced from the orbifold Mariño-Vafa formula in[19].Thus the classical λg-conjecture is contained in the orbifold version of Mariño-Vafa formula.
Moreover,we obtain a recursion formula of the λ1λg-type Hurwitz-Hodge integrals.

where C(g,l,b1,···,bl,a)is a constant depending only on the Hodge integrals
This formula generalizes Theorem 1.5 in[23].
The paper is organized as follows.In Section 2 and Section 3,we review the fundamental notions and the Laplace transform of the cut-and-join equation in[23]and[25].The main results of this paper is in Section 4,where we give the recursion formula for several types of the Hurwitz-Hodge integrals.As an application,we reprove Theorem 1.1 and obtain the recursion formula mentioned above.
2 The Cut-and-Join Equation of Orbifold Gromov-Witten Vertex
We follow the notations used in[19].Letbe the moduli space of stable maps to the classifying space BZawhere γ=(γ1,···,γn)is a vector of elements in Za.In particular,when a=1,the moduli space of stable mapsis specialized toLet U be the irreducible C-representation of Zagiven by

We have the corresponding Hodge bundleand the Hodge classesci(EU).More generally,for any irreducible representation R of Za,we denote the corresponding Hodge bundle and Hodge classes as ERand λRi,respectively.
The i-th cotangent line bundle Lion the moduli space of curves has fi berThe ψ-classes on Mg,nare de fined as

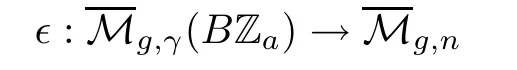
as

The Hurwitz-Hodge integrals overare the top intersection products of the classes

The Hurwitz-Hodge integrals are associated with the classical Hurwitz numbers[14]:

De fi ne
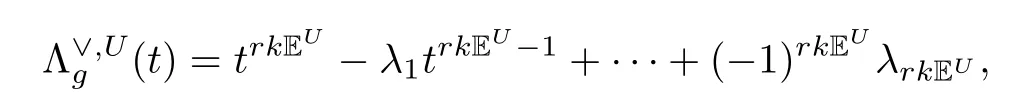
where rkEUis the rank of EUdetermined by the orbifold Riemann-Roch formula.
Let d be a positive integer and letµ=(µ1,···,µl(µ))be a partition of d,i.e.,d.We require γ=(γ1,···,γn)to be a vector of nontrivial elements in Zaand viewµas a vector of elements in Za.Then for any τ∈Z,we de fi ne Gg,µ,γ(τ)as


where γ−µdenotes the vector(γ1,···,γn,−µ1,···,−µl(µ)),corresponds toµi,U∨and 1 denote the dual of the representation U and the trivial representation respectively.Here[x]is the integer part of x,〈x〉=x−[x],and

Moreover,we de fi ne

Let p=(p1,p2,···,pn,···)and x=(x1,···,xa−1)be the formal variables.De fi ne pµ= pµ1···pµl(µ),xγ=xγ1···xγn.
De fi ne the generating functions

For the sake of convenience,we introduce the notation

Therefore,

According to the cut-and-join analysis illustrated in[24],for any g≥1,partitionsµand γ,we get the following theorem obtained in[22]by comparing the coeffi cients of λ2g−2+l(µ)pµxγ.
Theorem 2.1([22]Theorem 2.1)The one-legged orbifold Gromov-Witten vertex Gg(µ,γ,τ)asatisfies the following equation:

3 The Laplace Transform of the Cut-and-Join Equation
Recall the de finition of Gg,µ,γ(τ)ashowed in Section 2,we have δ=1 when all monodromies around loops on the domain curve are trivial,i.e.,γ=φ and a|µi,for all 1≤i≤l(µ).In the following sections,we restrict ourselves to the special case.
Since a|µi,there exists νi∈Z+such that for every 1≤i≤l(µ),µi=aνi.Obviously,ν=(ν1,···,νl(µ))is the partition such thatµ=aν.Whenµ=aν and γ=∅,we introduce the notations Gg,ν(τ)aand Gg(ν,τ)ato denote Gg,µ,γ(τ)aand Gg(µ,γ,τ)a,respectively.
According to the de finition of Gg,µ,γ(τ)a,we have

For the unstable integrals,we should use the following conventions

Therefore

3.1The Laplace Transform of Gg,ν(τ)a
We introduce the following notation for Hurwitz-Hodge integral

By a direct calculation,we have


De fi ne the Laplace transform of Gg,ν(τ)aas

where l=l(ν).
This formula can be viewed as a generalized version of formula(6)in[22].
In[22],Zhu showed that the Laplace transform of Gg,ν(τ)ahas a nice expression in the new variable t:

3.2The Laplace Transform of the Cut-and-Join Equation
In our case,the cut-and-join equation is reduced to

In[22],the author established the following Laplace transform of the cut-and-join equation.
Theorem 3.1([22]Theorem 3.5)The Laplace transform of the cut-and-join equation for Gg,ν(τ)atakes the following form:

4 Hurwitz-Hodge Integral Identities
In this section,we derive several Hurwitz-Hodge integral identities from formula(3.3).
4.1Preliminary Calculations
For the sake of convenience,we rewrite formula(3.3)as follows:
For g≥1 and l≥1,

where



Simultaneously,

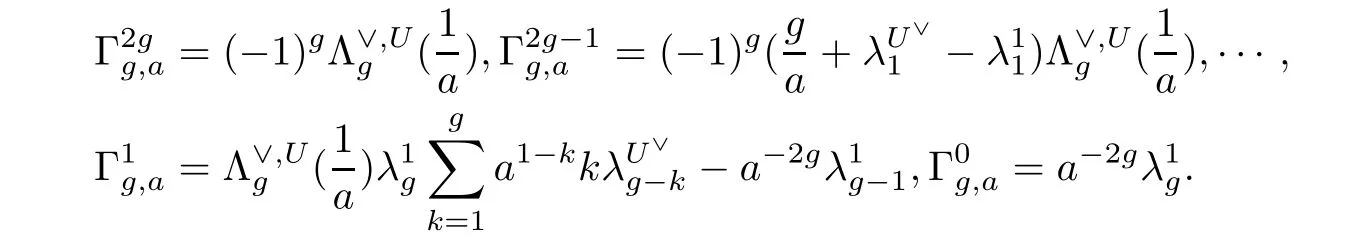
Here we only list the following formulas which are required in our paper:

It is clear that the recursion relation foris the same as the de finition ofin[10]and they share the same initial value.Hence
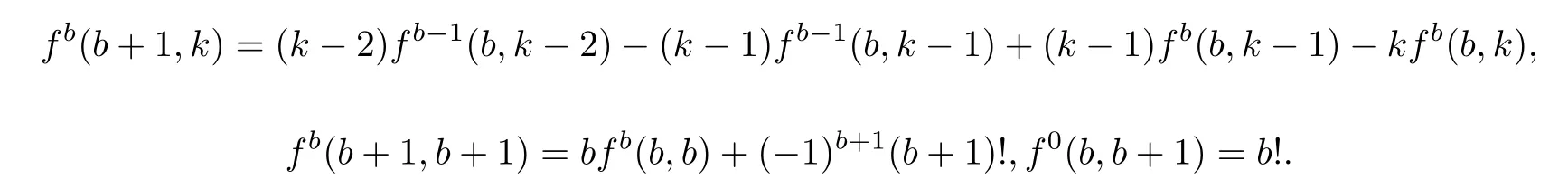
For the details,refer to[23].
Substituting(4.5)and(4.6)into(4.1),(4.2),(4.3)and(4.4),one gets
Theorem 4.1LHS=T1+T2+T3,where


4.2Expand at In finity
For b≥0,one can expand at τ=∞as
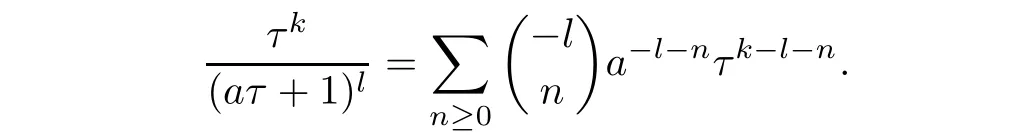
For example,the term containing τ in(4.7)is

It is easy to see that the largest degree of τ is 2g+l−3 in formulas(4.7)-(4.10).If F(t,τ)∈ Q[t][[τ]],we use the notation[τk]F(t,τ)to denote the coeffi cient of τkin F(t,τ).Byand some calculations,we obtain that

Corollary 4.2

This is a generalization of Theorem 1.1 in[10],which was studied by many people to derive DVV equation[5,17],λg-conjecture[17]and λg−1Hodge integral recursion[24].
Obviously,we can obtain more such corollaries by the same procedure.For example,bywe have


Then,we also get a Hurwitz-Hodge integral identity from identity(4.13)=(4.14)+(4.15)+(4.16)which contains the Hurwitz-Hodge integralBy the same procedure,we can calculate all the Hurwitz-Hodge integral of the typek=1,···,g.However,the computation is far more complicated,so we have not written down the explicit formulas.
4.3A Proof of Theorem 1.1
Now we consider the expansion ofIt is easy to see that the lowest degree of τ in formula(4.7)is l−2.Bywe have

Therefore,we have
Corollary 4.3

Considering the constrained dimension condition,we have|bL|=2g−3+l and e=bi+bj−1,then we have
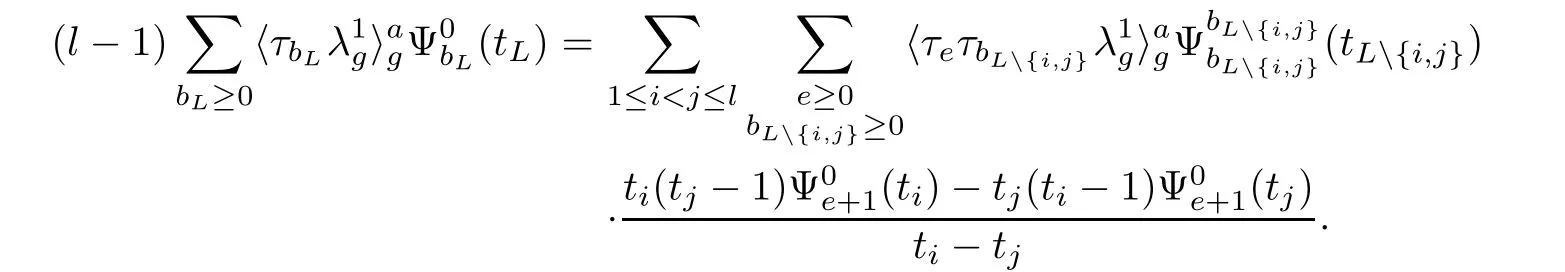
We now introduce two notations for the following expositions.Let

Denote

Applying the two operators on the corollary and taking the largest degree at both sides,we have

It follows that

Therefore,we obtain
Corollary 4.4
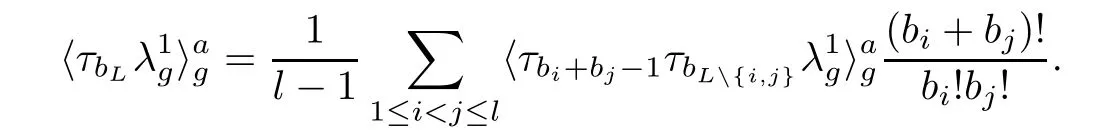
By the induction on l,we get the λg-integral formula:

4.4Sub-Lowest Degree Case
We calculate the sub-lowest degree of τ.

By|bL|=2g−3+l and|bL{i,j}|+e=2g−4+l,we have



Substituting(4.23)into identity(4.19)=(4.20)+(4.22),we obtain the corollary
Corollary 4.5


4.5A Recursion Formula for Hodge Integral
Thus,we have

where C(g,l,b1,···,bl,a)is a constant depending only on the Hodge integrals
ProofTaking all the terms with degree 2g+2l−4 in Corollary 4.5,we have

It follows that


We give an example to illustrate the constant term Ca(g,l,b1,···,bl)mentioned in the previous theorem.
Example 4.7Consider the case l=2.
Let b1+b2=2g−2.Take the term of degree 2g in Corollary 4.5,we have


Taking the coeffi cient of termon both sides,

Hence

In other words,when l=2,the constant term in(4.24)is

AcknowledgementsThe author would like to thank Professor Kefeng Liu for his encouragement and thank deeply Dr.Shengmao Zhu for his helpful discussion and valuable suggestions.The author is grateful to the Centre of Mathematical Sciences,Zhejiang University for their support and the wonderful research environment.
References
[1]Abramovich D,Graber T,Vistoli A.Gromov-Witten theory of Deligne-Mumford stacks.Amer J Math,2008,130(5):1337-1398
[2]Bryan J,Graber T.The crepant resolution conjecture.Proc Sympos Pure Math,2009,80:23-42
[3]Bryan J,Graber T,Pandharipande R.The orbifold quantum cohomology of C2/Z3and Hurwitz-Hodge integrals.J Alg Geom,2008,17(1):1-28
[4]Cavalieri R.Generating functions for Hurwitz-Hodge integrals.Adv Math,2008,218(5):1419-1429
[5]Chen L,Li Y,Liu K.Localiztion,Hurwitz numbers and the Witten conjecture.Asian J Math,2008,12(4):511-518
[6]Costello K.Higher-genus Gromov-Witten invariants as genus 0 invariants of symmetric products.Ann Math,2006,164(2):561-601
[7]Chen W,Ruan Y.Orbifold Gromov-Witten theory//Orbifolds in Mathematics and Physics.Contemp Math 310,Madison,WI.Providence,RI:Amer Math Soc,2002:25-85
[8]Dixon L,Harvey J A,Vafa C,Witten E.Strings on orbifolds.Nucl Phys B,1985,261:678-686
[9]Dixon L,Harvey J A,Vafa C,Witten E.Strings on orbifolds(II).Nucl Phys B,1986,274(2):285-314
[10]Eynard B,Mulase M,Safnuk B.The Laplace transform of the cut-and-join equation and the Bouchard-Mariño conjecture on Hurwitz numbers.Publ Res Inst Math Sci,2011,47(2):629-670
[11]Faber C,Pandharipande R.Hodge integrals,partition matrices,and the λgconjecture.Ann Math,2003,157(1):97-124
[12]Jarvis T,Kimura T.Orbifold quantum cohomology of the classifying space of a finite group//Contemp Math 310,Madison,WI.Providence,RI:Amer Math Soc,2001:123-134
[13]Jiang Y,Tseng H H.On virasoro constraints for orbifold Gromov-Witten theory.Int Math Res Not,2010,4:756-781
[14]Johnson P,Pandharipande R,Tseng H H.Abelian Hurwitz-Hodge integrals.Michigan Math J,2011,60:171-198
[15]Li Y.Some results of the Mariño-Vafa formula.Math Res Lett,2006,13:10001-10018
[16]Liu C-C.Localization in Gromov-Witten theory and orbifold Gromov-Witten theory//Handbook of moduli(Vol II).Adv Lect Math,25.International Press and Higher Education Press,2013:353-425
[17]Mulase M,Zhang N.Polynomial recursion formula for linear Hodge integrals.Commun Number Theory Phy,2010,4(2):267-294
[18]Tseng H-H.Orbifold quantum Riemann-Roch,Lefschetz and Serre.Geom Topol,2010,14:1-81
[19]Zong Z.Generalized Mariño-Vafa formula and local Gromov-Witten theory of orbi-curves.arXiv:1109.4992[20]Zhou J.On computations of Hurwitz-Hodge integrals.arXiv:0710.1679
[21]Zhou J.From Hurwitz-Hodge integrals to Hodge integrals.preprint,2008
[22]Zhu S.The remodeling conjecture for orbifold Gromov-Witten theory of C3/Za.preprint,2013
[23]Zhu S.Hodge integral identities from the cut-and-join equation of Mariño-Vafa formula.Pure Appl Math Q,2013,8(4):1147-1177
[24]Zhu S.Hodge integrals with one λ-class.Sci China Math,2012,55(1):119-130
[25]Zhu S.On the recursion formula for double Hurwitz numbers.Proc Amer Math Soc,2012,140(11):3749-3760
[26]Luo W,Zhu S.Hurwitz-Hodge integral identities from the cut-and-join equation.To appear in Annals of Combinatorics
[27]Hu J.Quantum cohomology of blowups of surfaces and its functoriality property.Acta Math Sci,2006,26(4):735-743
[28]Yang Y.Electrically charged solutions in gauge ã theory.Acta Math Sci,2010,30B(6):1975-2005
[29]Lin J.Natural Frobenius submanifolds.Acta Math Sci,2010,30B(3):873-889
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- SOME STABILITY RESULTS FOR TIMOSHENKO SYSTEMS WITH COOPERATIVE FRICTIONAL AND INFINITE-MEMORY DAMPINGS IN THE DISPLACEMENT∗
- STABILITY OF VISCOUS SHOCK WAVES FOR THE ONE-DIMENSIONAL COMPRESSIBLE NAVIER-STOKES E QUATIONS WITH DENSITY-DEPENDENT VISCOSITY∗
- STABILITY ANALYSIS OF A COMPUTER VIRUS PROPAGATION MODEL WITH ANTIDOTE IN VULNERABLE SYSTEM∗
- STABILITY OF A PREDATOR-PREY SYSTEM WITH PREY TAXIS IN A GENERAL CLASS OF FUNCTIONAL RESPONSES∗
- NONSMOOTH CRITICAL POINT THEOREMS AND ITS APPLICATIONS TO QUASILINEAR SCHRÖDINGER EQUATIONS∗
- NORMAL FAMILIES OF MEROMORPHIC FUNCTIONS WITH SHARED VALUES∗
