长方体单腔室空腔环境内爆炸效应的实验研究*

胡 洋，朱建芳，朱 锴

(华北科技学院安全工程学院矿井灾害防治重点实验室，北京 101601)

长方体单腔室空腔环境内爆炸效应的实验研究*

胡 洋，朱建芳，朱 锴

(华北科技学院安全工程学院矿井灾害防治重点实验室，北京 101601)

为了获得在典型空腔内发生爆炸后，结构壁面上爆炸载荷的分布规律和空腔结构的破坏形式，以国防工事和人防工事的等级设计规范为依据，设计了长方体单腔室空腔模型，并对该模型进行了药量逐渐递增直至可使结构破坏的内爆炸实验。用压力传感器和加速度传感器分别记录了单腔室壁面上爆炸载荷的压力时程曲线和结构壁面振动的加速度时程曲线，分析了壁面上爆炸载荷的分布规律以及模型结构的破坏形式，并将首个峰值的实测数据与理论计算和数值模拟结果进行了对比，探讨了3种研究方法产生误差的原因。

爆炸力学；爆炸效应；内爆炸；典型空腔

随着近年来世界各地恐怖事件的不断发生，大批学者对地下防御工事的相关问题进行了大量研究[1-4]。典型空腔环境内爆炸效应研究就是这类问题中重要的一项，这项研究包括对空腔环境壁面上爆炸载荷分布规律和结构振动等问题的研究，其实质是为典型空腔环境的强度设计提供依据。目前，对这类问题的研究主要采用3种方法:理论计算、数值模拟和模型实验[5-8]。由于空腔环境内爆炸流场形成过程复杂，因此在理论推导过程中很难建立一个合理的数学模型来求得精确的解析解；数值模拟的优点在于可以再现空腔环境内爆炸冲击波流场的演变过程，缺点则是很难找到与材料吻合的计算参数，因此会导致计算结果产生一定的误差，同时数值模拟要求网格划分得十分细致，这也对计算机硬件提出了很高的要求；模型实验则可以通过分析实测曲线的峰值和波形来得到较精确的结论。目前空腔环境内爆炸模型实验大多是在已有的爆炸塔或爆炸罐中进行的，而本文中拟根据工程中的具体要求设计一套实验装置，通过实验现象和实测的实验数据分析爆炸载荷的分布规律和模型结构的破坏形式，以期为下一步各类密闭腔室环境内爆炸效应问题的研究提供理论依据。

1 空腔环境实验模型设计

1.1 单腔室空腔环境

根据国防工事和人防工事的等级设计规范[9]，空腔环境内防护单元隔墙的等效静载荷是爆炸冲击波超压峰值的1/4～1/8，考虑到本次的实验模型要能进行多次实验，所以设计防护单元隔墙的等效静载荷为爆炸冲击波超压，即防护单元隔墙的等效静载荷为1.2 MPa。

根据在钢筋混凝土结构设计中纵向受力钢筋的配置要求[10]，本文的实验模型可以简化为内部静压为1.2 MPa的长方体钢筋混凝土密闭腔室，腔室的主体采用C35级混凝土，钢筋采用HRB400级螺纹钢筋，钢筋的尺寸、数量和间隔根据混凝土设计规范进行计算。由于爆炸冲击波超压均匀作用在腔室的内壁上，因此钢筋混凝土结构的侧壁在纵向受拉伸作用，且整个构建处于轴心受拉状态。轴心受拉构建在破坏时所能承受的拉力可由下式求得：

N≤fyAs

(1)

式中：N为轴向拉力设计值，fy为钢筋抗拉强度设计值，As为纵向受拉钢筋截面面积。

N≤Nu/γd=fyAs/γd

(2)

所需钢筋总横截面积为：

As=γdN/fy

(3)

式中：γd为结构因数；查表得HRB400钢筋的fy=400 MPa。

此外，最小配筋率还要求：As≥0.4%S以及As≥90ftS/fy，ft为混凝土抗拉强度设计值，查表[11]得C35混凝土的ft=1.57 MPa。

根据以上的混凝土设计要求，计算得到的结果见表1，表中ps,e为等效静载荷，a为结构的长度，b为结构的宽度，c为结构的高度，S为结构内表面积，l为结构壁面周长，F为钢筋拉力，f为钢筋强度，d为钢筋直径，n为钢筋根数，δ为钢筋层数，k为钢筋间隔。

表1 结构壁面纵向钢筋参数Table 1 Reinforcement parameters of longitudinal wall

表1是根据静压力在结构壁面上的作用力计算得到的数值，根据等效静载荷是爆炸冲击波超压峰值的1/8～1/4，保守估计该壁面上可以承受2.4～3.6 MPa的爆炸冲击载荷，由冲击波在刚性壁面上的反射超压经验公式[12]：

(4)

可以得到入射波的超压值为0.56～0.80 MPa，式中：Δp2为冲击波的反射超压，Δp1为冲击波的入射超压，p0为标准大气压。再由萨多夫空爆经验公式[13]：

(5)

可以得出实验中的最大药量至少可达200 g，式中：Z=RW-1/3,R为特征点距离爆心的距离(m)，W为炸药的质量(kg)。

单腔室密闭结构采用C35级混凝土和直径14 mm的HRB400级钢筋;内腔长、宽、高分别为3 000、1 500、1 500 mm，壁厚150 mm。钢筋在结构厚度方向双层排列，间隔100 mm；在结构长度方向钢筋排列16层，间隔为190 mm；在结构宽、高度方向钢筋排列8层，间隔也为190 mm，具体结构见图1～2。

1）随着压力机技术的发展，使用伺服压力机代替传统机械压力机，可以将冲压的噪声控制在75dB以下，达到非常理想的效果。

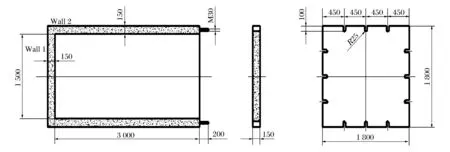
图1 密闭腔室结构尺寸(单位为mm)Fig.1 The geometry size of a closed chamer (unit in mm)

图2 浇筑前的实验模型Fig.2 The experimental model before pouring

1.2 实验测量设备

实验中采用CY-YD-205型压力传感器捕捉压力信号，传感器的量程为0～5 MPa，压力高于0.1 MPa时立即触发。整个实验模型中共布置5个观测点，分别设置在2个相邻的侧墙壁面上，传感器安放在实验装置侧墙的预留孔内，并确保传感器的压力感受面与实验装置内壁平齐，具体位置如图3所示。

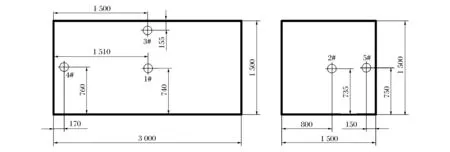
图3 观测点即压力传感器安装具体位置示意图(单位为mm)Fig.3 Schematic layout of pressure sensors (observation points) (unit in mm)

图4 实验药柱实物实物图Fig.4 A photo of experimental explosive charges

1.3 爆炸源

共进行了5次空腔环境内爆炸实验，爆炸源分2种:一种是单块质量为75 g的圆柱状TNT炸药，另外一种是单块质量为200 g的块状TNT炸药，用铝制8号电雷管起爆，每一发实验的装药位置均在实验装置的中心处，实验药柱如图4所示。

2 实验结果

2.1 实测的爆炸载荷波形

每一发实验后传感器都记录下壁面上5个观测点的压力时程曲线，从实测的冲击波波形来看，实验装置角域处传感器波形较乱，其他位置传感器的实测波形较规则。

针对药量为75 g的情况共进行了3次模型实验，图5给出了3次实验中相邻壁面上5个观测点的实测压力(p)时程曲线和数值模拟曲线。从图5可以看出，作用在结构壁面上的爆炸载荷，初始为脉冲载荷，其峰值超压较大，而作用时间较短，脉冲有多个，一般情况下脉冲峰值呈锯齿形依次迅速降低，此后形成准静态压力，上述特点在图5(a)中体现得最明显，观测点的首次压力峰值达到1.38 MPa，比解析解[14](自由大气空爆相应比例距离爆炸处反射压力峰值)高约64%；在结构壁面上的某些区域，由于空腔环境壁面的约束作用使大量冲击波叠加，爆炸流场变得相当复杂，其后续峰值甚至会超过初始脉冲峰值，这一特点在图5(b)中体现得最明显，观测点的首个压力峰值为0.19 MPa，而最大压力出现在第4个波峰，其最大值为1.71 MPa，是首个峰值的9倍。

表2展示了不同药量下理论计算、数值模拟和实测数据的对比。

图5(a) 观测点1的实测冲击波波形
Fig.5(a) Overpressure-time curves of shock waves measured at observation point 1

图5(b) 观测点2的实测冲击波波形
Fig.5(b) Overpressure-time curves of shock waves measured at observation point 2

图5(c) 观测点3的实测冲击波波形
Fig.5(c) Overpressure-time curves of shock waves measured at observation point 3

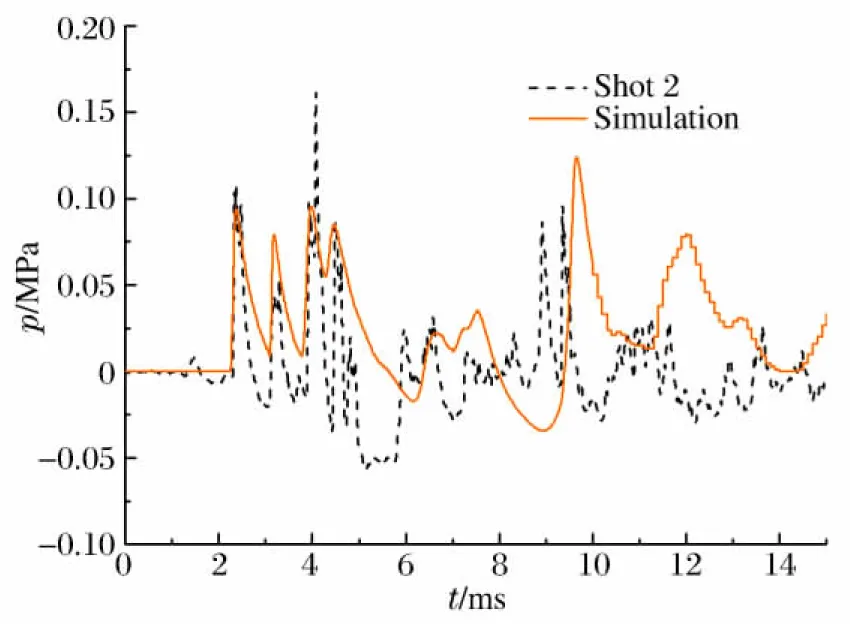
图5(d) 观测点4的实测冲击波波形
Fig.5(d) Overpressure-time curves of shock waves measured at observation point 4

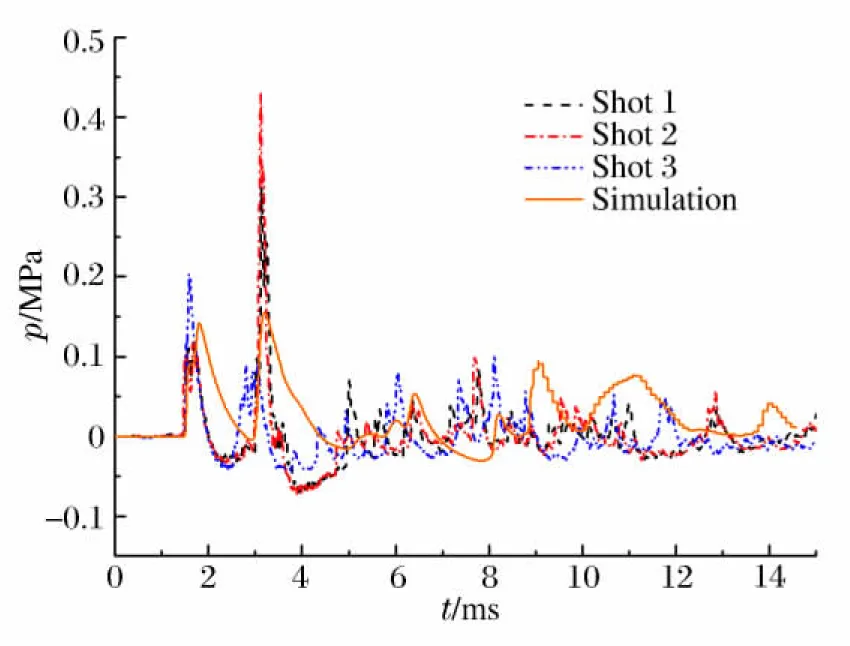
图5(e) 观测点5的实测冲击波波形
Fig.5(e) Overpressure-time curves of shock waves measured at observation point 5

从表2可以看出，首个峰值理论计算、数值模拟和实测结果之间存在一定的误差，造成这种误差的原因有很多。如在数值模拟研究方面,目前爆炸类问题一般采用LS-DYNA软件，该程序具有Lagrange、Euler和ALE算法，这3种算法得到的计算结果存在着一定的差异：拉格朗日算法由于计算网格的畸变，可能直接影响计算精度甚至使计算终止；欧拉算法则网格数量过大，会占用很多的计算机资源；ALE算法采用了Lagrange和Euler两种算法执行自动重分区，即执行一步或者几步Lagrange计算，当单元网格随材料流动产生变形时再执行ALE计算。同样网格的划分对计算结果也存在一定的影响，T.C.Chapman等[15]在计算冲击波超压时，发现计算网格长度由10 mm缩减到1 mm时，计算结果可提高24.6%。由此可见，计算方法、网格划分、计算机硬件条件等因素将直接决定计算结果的准确性。而在实验方面，单腔室箱体的密封性、传感器的安装位置以及炸药的装药形状等因素也都会对实验结果造成一定的影响。以观测点1和观测点2这2个正反射点为例，与理论计算相比较，数值模拟的误差在30%左右，而实测结果的误差则在10%左右。

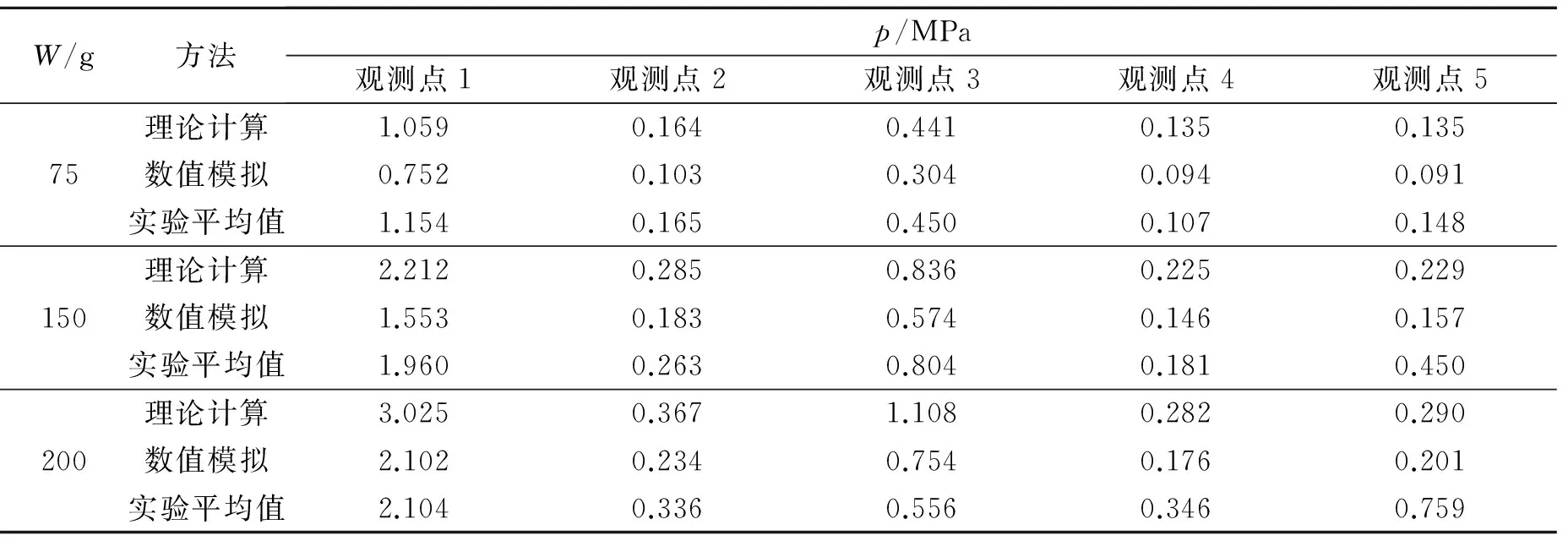
表2 5个观测点首次反射的理论计算、数值模拟及实测结果的比较Table 2 Comparison among theoretical calculation, numerical simulation and experimental results for the first reflection at five observation points

2.2 结构破坏形式

2.2.1 实验现象

由于实验是在密闭单腔室内进行，且结构密封性较好，因此炸药爆炸释放的能量大部分转化为对结构模型的冲击能，并且作用时间很长。当药量为75 g时，模型结构几乎未见明显裂纹，炸药对结构的破坏效应不大。当药量增加到150 g时，实验装置顶部表面出现裂纹，裂纹主要出现在爆心投影点周围。当药量增加到200 g时，炸药对模型的破坏作用较明显，顶部裂纹进一步增加，裂纹最宽处可达到1 cm，裂纹长达到3 m，打开实验装置门后发现结构侧壁和顶部连接处出现较严重的开裂，结构侧壁有明显的弯曲变形，局部混凝土被压碎脱落。造成这一现象的主要原因是：混凝土承受爆炸载荷作用前已经含有一些微小裂纹，在爆炸载荷作用下微小裂纹萌生、扩展、贯通，直至产生宏观裂纹，并逐渐失去了承载能力。图6给出了200 g炸药爆炸后结构模型的破坏情况。

图6 200 g装药爆炸后结构模型的破坏情况Fig.6 Destruction of the model after explosion of 200 g TNT

2.2.2 加速度曲线分析

以75 g药量为例，对壁面上几个观测点进行简单的振动分析，图7给出了实验中几个观测点加速度的实测曲线。

从图7可以看出，观测点1的振动加速度最大，达到了400个重力加速度，这一结果与实验现象也较吻合，装置出现较大裂纹处主要集中在爆心投影点周围，即观测点1；从实测的压力时程曲线可知，观测点2出现了多个超压峰值，这是由于空腔环境内爆炸冲击波流场的叠加造成的，因此观测点2的振动加速度也体现出了多个峰值的特点。

图7 75 g装药爆炸后不同观测点的加速度时程曲线Fig.7 Acceleration-time curves at different observation points after explosion of 75 g TNT

3 结 语

(1)在结构壁面上的某些区域爆炸载荷的分布规律与W.E.Baker等[16]提出的内爆炸载荷的多三角形脉冲算法基本一致，初始为脉冲载荷，其峰值超压较大，而作用时间较短，脉冲有多个，一般情况下脉冲峰值呈锯齿形依次迅速降低，此后形成准静态压力；而壁面上的另一些区域由于受到密闭腔室壁面的约束作用，爆炸冲击波大量叠加使得爆炸流场十分复杂，因此出现了后续冲击波峰值会超过初始脉冲峰值的现象，用于描述这一现象的数学模型还有待进一步研究。

(2)当炸药对结构的破坏作用达到一定程度时，结构各个壁面有明显的弯曲变形，爆心投影处会向外鼓胀，按照塑性铰线形式的破坏行为是箱体结构内爆炸破坏的特点[17]；结构模型角域附近由于冲击波的汇聚作用，因此与其他部位相比更容易被破坏，实验中可以看到侧墙和顶部连接处会出现明显的长条裂纹，在今后的结构强度设计中应引起重视。

[1] Wharton R K, Formby S A, Merrifield R. Air blast TNT equivalence for a range of commercial blasting explosives[J]. Journal of Hazardous Materials, 2000,79(l/2):31-39.

[2] 李国豪.工程结构抗爆动力学[M].上海:上海科学技术出版社,1989:3-10.

[3] Rigas F, Sklavounos S. Experimentally validated 3-D simulation of shock waves generated by dense explosives in confined complex geometries[J]. Journal of Hazardous Materials, 2005,121(l/2/3):23-30.

[4] 张亚军.爆炸流场及容器内爆流固耦合问题计算研究[D].合肥:中国科学技术大学,2007:9-13.

[5] 胡八一，李平，张振宇，等.爆炸塔内壁特征点的反射压力数值模拟[J].计算力学学报,2009,26(4):573-578. Hu Bayi, Li Ping, Zhang Zhenyu, et al. Numerical simulation of characteristic points reflective pressure on the inner surface of the explosion chamber[J]. Chinese Journal of Computational Mechanics, 2009,26(4):573-578.

[6] 朱文辉，薛鸿陆，刘仓理，等.爆炸容器承受内部加载的实验研究[J].爆炸与冲击,1995,15(4):374-381. Zhu Wenhui, Xue Honglu, Liu Cangli, et al. Experimental study on the explosive chambers under internal blast loading[J]. Explosion and Shock Waves, 1995,15(4):374-381.

[7] 曹玉忠，卢泽生.抗爆容器内爆炸流场数值模拟[J].高压物理学报,2001,15(2):127-133. Cao Yuzhong, Lu Zesheng. Numerical simulations of blast flowfields in closed blast-resistance containers[J]. Chinese Journal of High Pressure Physics, 2001,15(2):127-133.

[8] 王可强，苏经宇，王志涛.爆炸冲击波在建筑群中传播规律的数值模拟研究[J].中国安全科学学报,2007,17(10):121-127. Wang Keqiang, Su Jingyu, Wang Zhitao. Numerical simulation of propagation rules of blast shock wave in building cluster[J]. China Safety Science Journal, 2007,17(10):121-127.

[9] 过镇海.钢筋混凝土原理[M].北京:清华大学出版社,1999:26-40.

[10] 宁建国，商霖，孙远翔.混凝土材料动态性能的经验公式、强度理论与唯象本构模型[J].力学进展,2006,36(3):389-403. Ning Jianguo, Shang Lin, Sun Yuanxiang. The research developments of dynamic constitutive relationship for concrete[J]. Advances in Mechanics, 2006,36(3):389-403.

[11] 卢国强.钢筋混凝土-钢板组合结构抗爆炸作用的试验研究与动力分析[D].上海:同济大学,1997:45-48.

[12] 李翼祺.爆炸力学[M].北京:科学出版社,1992:99-107.

[13] 亨利奇.爆炸动力学及其应用:1979年版[M].熊建国,等,译.北京:科学出版社,1987:76-83.

[14] TM5-855-1, Fundamentals of protective design for conventional weapons[M].方秦,译.南京:工程兵工程学院,1997:35-42.

[15] Chapman T C, Rose T A, Smith P D. Blast wave simulation using AUTODYN2D: A parametric study[J]. International Journal of Impact Engineering, 1995,16(5):777-787.

[16] Baker W E, Cox P A. Explosion hazards and evaluation[M]. New York: Elsevier Publishing Company, 1983:15-18.

[17] 郭志昆，宋锋良，刘峰，等.扁平箱形密闭结构内爆炸的模型试验[J].解放军理工大学学报:自然科学版,2008,9(4):345-350. Guo Zhikun, Song Fengliang, Liu Feng, et al. Experiment of closed flat box structure subjected to internal detonation[J]. Journal of PLA University of Science and Technology: Natural Science Edition, 2008,9(4):345-350.

(责任编辑 张凌云)

Experimental study on explosion effect in a closed single rectangular cavity

Hu Yang, Zhu Jianfang, Zhu Kai

(KeyLaboraryofMineDisasterPreventionandControl,SafetyEngineeringCollege,NorthChinaInstituteofScienceandTechnology,Beijing101601,China)

According to the design specifications of national defense works and human defense works, a closed single rectangular cavity model was developed to obtain the explosion load distribution at the walls of typical cavities and the corresponding destruction forms resulted from the explosion inside the cavities. The developed cavity model was applied to carry out internal explosion experiments, in which the mass of the TNT charge was increased gradually until the cavity model could be damaged. Pressure and acceleration sensors were used to record the explosion pressure-time curves and the vibration acceleration-time curves at the cavity walls, respectively. And the explosion load distributions at the cavity walls and the destruction form of the model structure were analyzed. The first peaks of the measured data were compared with the results of theoretical calculation and numerical simulation to discuss the cause for the errors among the three methods.

mechanics of explosion; explosion effect; internal explosion; typical cavity

10.11883/1001-1455(2016)03-0340-07

2015-03-25；

2015-09-15

华北科技学院创新团队项目(3142015021，3142014124)； 爆炸科学与技术国家重点实验室开放基金项目(KFJJ15-15M)

胡 洋(1979— )，男，博士，讲师，28770007@qq.com。

O381国标学科代码：13035

A