基于单元相交的混合网格精确守恒插值方法*

徐春光，董海波，刘 君

(大连理工大学航空航天学院，辽宁 大连 116024)

基于单元相交的混合网格精确守恒插值方法*

徐春光，董海波，刘 君

(大连理工大学航空航天学院，辽宁 大连 116024)

基于网格切割思想，发展了二维/三维混合网格条件下的单元相交算法，可精确计算任意两个多边形/多面体的交集。在此基础上，实现了基于单元相交(CIB/DC)的精确守恒插值算法。二维和三维验证算例表明，该方法能够保证插值过程中计算域内物理量的严格守恒，且具有比常规二阶插值更高的精度。

流体力学;守恒插值;单元相交;混合网格;局部超网格

在包含运动边界的非定常流动模拟中，流场物理空间随时间变化，边界运动导致网格也随时间变化，典型应用包括多体分离、机翼抖振颤振、舱门启闭等[1]。CFD计算一般采用运动嵌套网格、笛卡尔自适应网格和变形动网格等技术处理网格变化。在采用上述技术处理网格变化时，均涉及流场信息的插值问题[1-2]，即利用旧网格上的流动信息插值获得重构区域流动参数。此外，在爆轰流场模拟中，爆轰计算网格与冲击波传播计算网格差两个量级[3-4]，为提高计算效率，往往需要将物理量由爆轰计算时使用的密网格插值传递到冲击波传播模拟中的疏网格。

插值过程一般应具备守恒性和单调性等基本特性。对爆轰计算等守恒性要求高的问题，一般的插值不能保证计算区域内物理量的守恒，会降低计算精度，且无法捕捉激波的正确位置[5]，需要发展守恒插值方法。守恒插值方法主要可分为两类，基于面通量(SFB/DC， simplified face-based donor-cell)的方法和基于单元相交(CIB/DC, cell-intersection-based donor-cell)的方法[6]。

SFB/DC方法[6]效率较高，但要求新、旧网格具有相同的拓扑结构，不适用于网格重构等拓扑发生变化的情况。CIB/DC方法思想简单直接，对计算网格的类型、结构不进行任何假设，适用范围很广，并且具有保号性，插值过程中不会产生新的极值[6]。但该方法推广至三维情况时，由于三维网格单元重叠区域切割计算非常复杂，给这种方法的应用带来了很大困难。为了实现严格意义下的三维CIB/DC算法，P.E.Farrell等[7]进行了一系列卓有成效的工作，在2011年进一步发展为“局部超网格”(Local Supermesh)方法，成功实现了非结构网格下的三维CIB/DC算法[8]。

本文中在P.E.Farrell等和S.Menon等[9]工作的基础上，构造了应用于二维/三维混合网格的CIB/DC算法，实现了基于精确网格切割的积分守恒插值。验证结果表明，该方法能够保证插值过程中计算域内物理量的严格守恒，具有比常规二阶插值更高的精度。

1 守恒插值基本思想

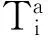
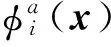
网格Tb是计算域Ω的另一种形式的划分，划分形式与要求同Ta，则同样有Tb上的物理量分布φb(x)。如果对于Ω的任意子区域D，满足如下条件：

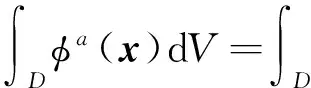
(1)

则称φb(x)是φa(x)的守恒插值结果。

对于一般的情形，要使式(1)满足，必须有Tb≡Ta，φb(x)≡φa(x)，但这就失去了在两套网格间进行插值的意义。为此，对D进行限制，不能是Ω的任意子区域，而必须是网格Tb中的某个网格：

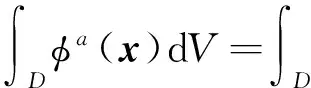
(2)

上式就是一般意义上的守恒插值关系式。

对式(2)，按照基于单元相交的思想，对D进行分解：

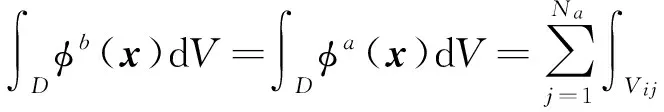
(3)

式(3)就是基于单元相交守恒插值方法(CIB/DC)的基本依据。从式(2)到式(3)未引入任何近似。因此，在给定分布φ(x)的情况下，CIB/DC方法是严格守恒的。

从式(3)还可以看出，如果已知网格Ta上的物理量分布φa(x)，如何计算网格单元间的相交区域Vij便成为CIB/DC方法的关键。

2 “超网格”基本思想

图1为文献[8]给出的超网格示意图，超网格是由Ta和Tb所有结点以及它们边界交点构成的网格，具有如下特性：

(1)每一个超网格不再和Ta或Tb中任何网格单元相交，即它总可以在Ta中找到一个网格包含或等于它，也总可以在Tb中找到一个网格包含或等于它；

(2)Ta的每一个网格总可以明确表示为一个或多个超网格的集合，Tb的每一个网格总可以明确表示为一个或多个超网格的集合。

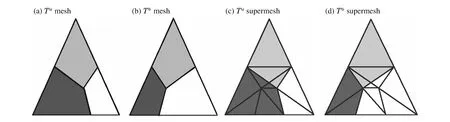
图1 超网格示意图Fig.1 Schematic of the supermesh

3 单元相交算法

由上节可知，获得超网格是实现精确守恒插值的关键。下面给出计算平面凸多边形和三维凸多面体交集的具体算法。

3.1 平面凸多边形相交算法

如图2所示，将目标三角形A1A2A3视为切割多边形，使用切割三角形B1B2B3对目标三角形进行切割，每次切割时只保留目标多边形中与切割多边形在切割线同侧的部分。图中依次使用△B1B2B3的3条边B1B2、B2B3、B3B1切割△A1A2A3，切割后保留的多边形依次为CA3A2G、CDEA2G、CDEFB1，多边形CDEFB1即为△A1A2A3和△B1B2B3的交集。

图2 二维网格切割示意图Fig.2 Schematic of the two-dimensional grid cutting

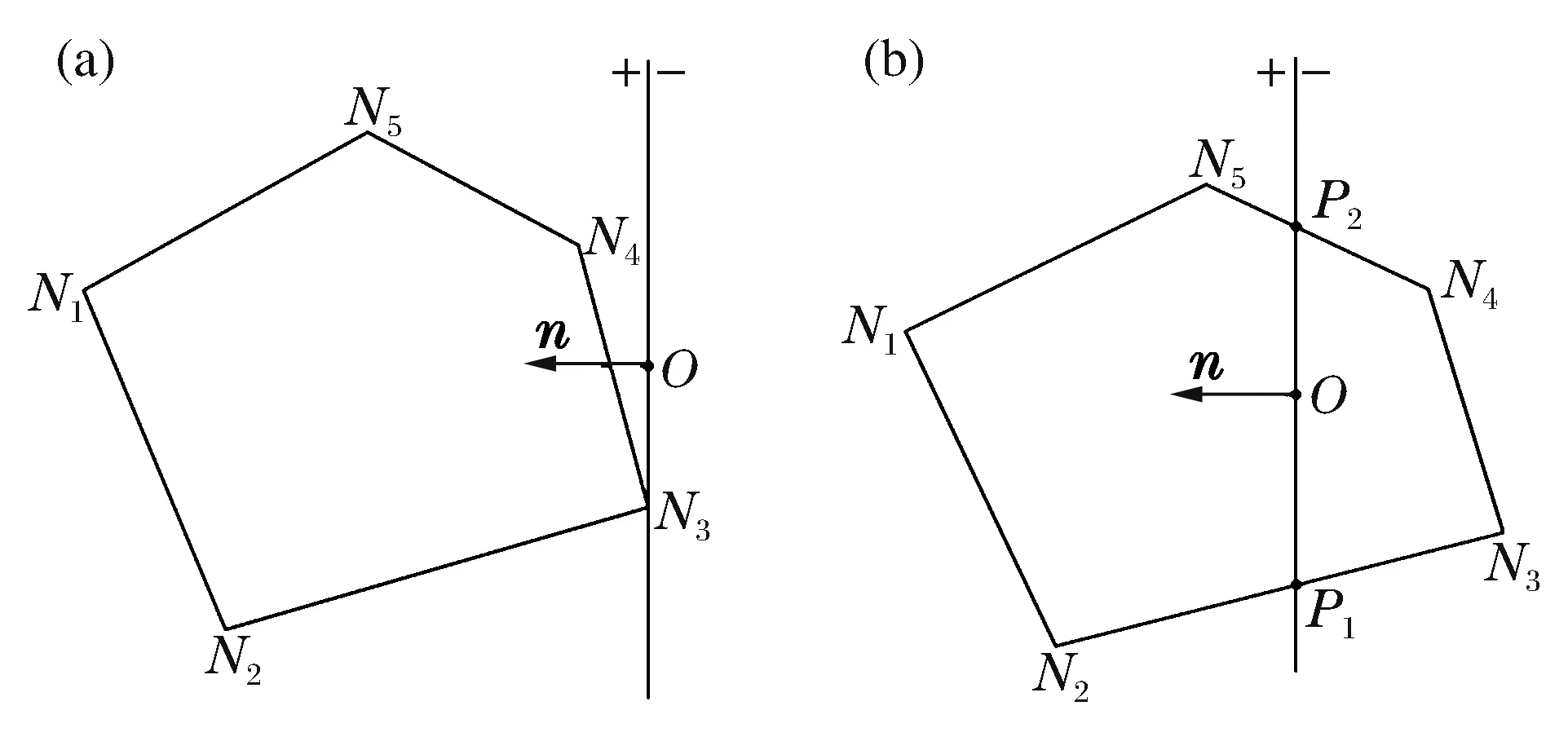
图3 直线切割平面凸多边形Fig.3 Schematic of a straight line cutting plane convex polygon

在使用直线去切割平面凸多边形时，以图3为例，切割直线经过点O，其法向单位矢量为n，切割直线将平面划分为两部分，定义法向n所指的半平面为正半平面，反方向的半平面为负半平面。如果切割之后目标多边形仅保留正半平面的部分，那么切割操作等效于求目标多边形和正半平面的交集。定义平面上任意一点P到切割直线的距离为：

d=xOP·n=(xP-xO)·n

式中：xP和xP分别为点P和点O坐标。

根据上述定义，正半平面的点到切割直线的距离均为正数，负半平面的点到切割直线的距离均为负数，切割直线上的点到切割直线的距离为零。如果凸多边形各顶点到切割直线的距离均为非负数(图3(a))，则切割结果即为原多边形；如果凸多边形各顶点到切割直线的距离均为非正数，则切割结果为空集；除上述两种情况外，凸多边形与切割直线必然有两个交点(图3(b))。具体如下：

(1)设目标多边形为N，其顶点依次为N1,N2,…,NN；切割直线为l，切割结果为R；

(2)计算N的各个顶点到l的距离，记顶点Ni到l的距离为di；

(3)初始化一个空的有序点集P；

(4)从顶点N1起，依次对多边形N的边N1N2,N2N3,…,NNN1进行判定。

对线段NiNj的判定过程为：如果didj<0，则线段与切割直线有新的交点，记交点为Nnew；依次将Ni、Nnew、Nj中距离为非负数的顶点加入点集P；如果didj≥0，则依次将Ni、Nj中距离为非负数的顶点加入点集P；

(5)完成所有边的判定后，如果P为空集，则R为空集；若P为非空集，则依次连接P中的点形成的多边形就是所求的切割结果R。

3.2 三维凸多面体相交算法

在三维流体计算中，常用的网格包括四面体、四棱锥、三棱柱、六面体等多种类型。其中，四棱锥、三棱柱、六面体这3种网格都具有四边形表面，网格生成过程中不能严格保证四边形表面的四个顶点位于同一平面内，会给多面体表面的定义带来歧义。

为了简化算法的复杂性，同时消除歧义，在计算两个任意凸多面体的交集时，首先将凸多面体分解为多个小四面体，如图4所示，其中点N6为点N2、N3、N4、N5的重心；然后通过计算这些小四面体的交集，来获得多面体的交集。计算多面体Pa和Pb的交集的具体步骤为：

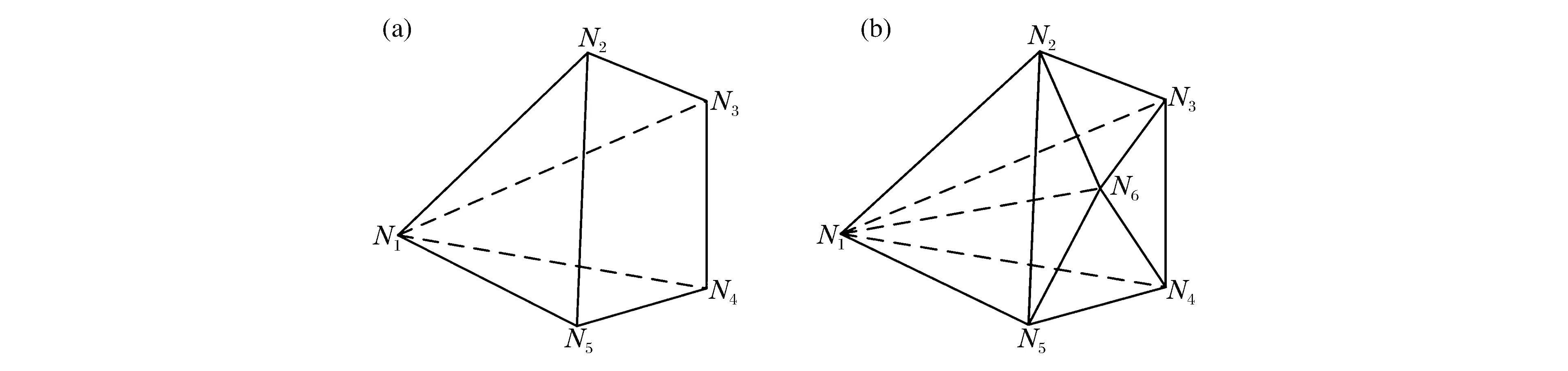
图4 三维网格分解示意图Fig.4 Schematic of the three dimensional mesh decomposition

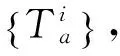
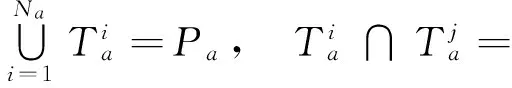
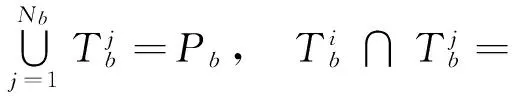
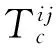
(3)多面体Pa和Pb交集可表示为：

交集的体积和重心分别是：

4 相交单元的搜索算法

相对于通常的流场插值方法，守恒插值的计算效率较低，主要有两个原因：(1)计算两个单元交集的算法较为复杂；(2)对同一个新网格单元，普通插值方法只需用到一个旧网格单元(称为贡献单元)的信息，而守恒插值需要用到多个贡献单元的信息。前文已对单元相交算法进行了详细的描述，本节将介绍守恒插值中多个贡献单元的搜索算法。

在贡献单元的搜索算法中，首先需要快速定位出新网格单元在旧网格中的位置。对此，可采用四叉树[11]或八叉树[12](三维)方法加速搜寻，如图5(a)所示，完全填充网格为旧网格，其上的非填充网格为新网格中的某个单元，通过四叉树方法，可快速定位出新网格单元的格心所在的旧网格单元(图中填充单元)，这是新网格单元的第1个贡献单元；然后，逐个搜索各个贡献单元的直接相邻单元，如果相邻单元与新网格单元相交，则将该单元加入贡献单元的列表，如图5(b)中浅色填充单元所示；当所有贡献单元的相邻单元(图5(c)与(b)中不同的填充单元)都不与新网格单元相交时，搜索结束。

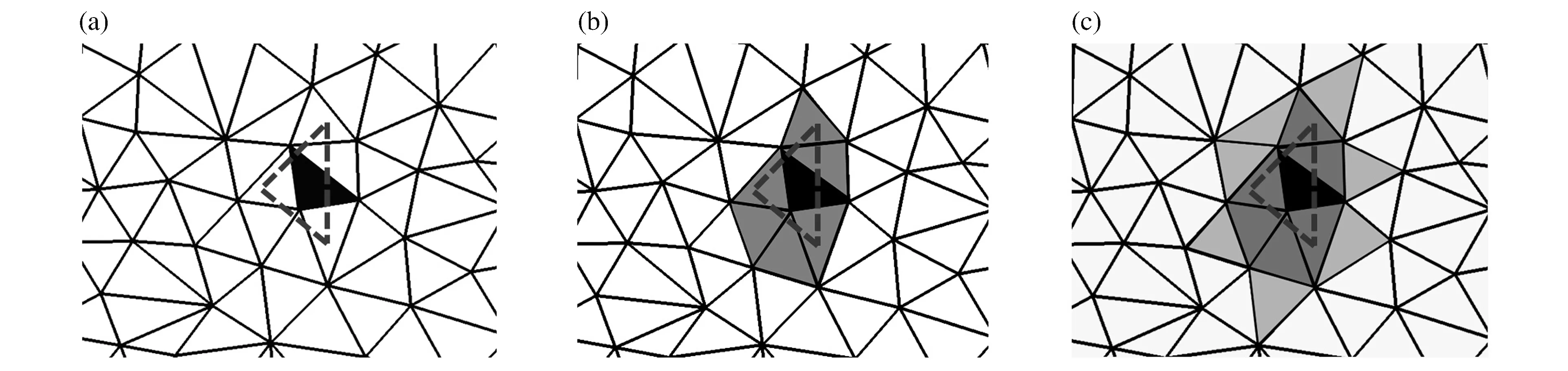
图5 相交单元的搜索方法Fig.5 Search method of intersection elements

5 守恒插值验证算例

图6 数值计算建模图Fig.6 Geometry of the specimen used for simulation

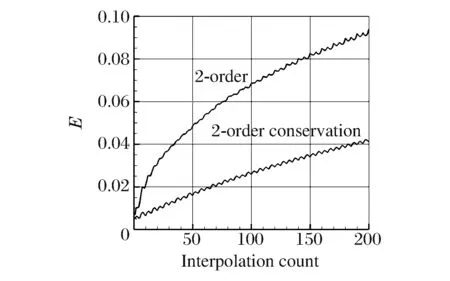
图7 计算结果的误差比较Fig.7 Different errors of computational results

图8 计算结果的积分比较Fig.8 Different integrals of computational results

设计了3个算例来验证本文发展的守恒插值方法。第1个算例主要考核相同拓扑结构下网格点位置变化的影响；第2个算例主要考核网格形状的影响；第3个算例主要考核三维情况下的应用情况。

算例1

考虑如下的测试函数：

φ(x,y)=1+sin(2πx)sin(2πy)

计算区域为[0,1]×[0,1]，计算网格为一组拓扑结构相同的非结构三角形网格，分别表示为M0、M1、…、MN，其中M0如图6所示。网格MN中的第(i,j)个网格点的坐标由下式给出：

式中：α(t)=0.5sin(4πt),ξ=(i-1)/(imax-1),η=(j-1)/(jmax-1)t=n/T,其中i=1,2,…,imax;j=1,2,…,jmax;n=0,1,…,N。

测试过程中，在网格M0上给定测试函数的准确分布，然后依次插值到网格M1、M2、…、MN上，共进行N次插值，最后比较网格MN上的函数分布与准确值之间的误差。在本文计算中，取imax=jmax=65，N=200，T=20。

图7给出了计算误差随插值次数的变化情况，其中纵坐标代表计算区域内各单元函数分布插值后计算值与理论值之差的1范数。两种插值方法中，插值误差都随插值次数的增加而增大，但守恒型插值方法的误差始终较小，不到常规二阶插值误差的一半。

图8为两种方法的物理量积分值比较，其中纵坐标代表每个单元计算值总和与理论值的比，从图中明显可以看出，守恒插值保证了计算域内物理量的守恒。

算例2

考虑如下的测试函数：

φ(r)=2+cos(πr/L)

计算区域是边长为1的正方形，L为正方形的对角线长度，r是与正方形中心的距离。测试中使用两种不同的网格，网格1是均匀分布的结构网格，网格2是非结构网格，并与网格1具有相同的边界网格点分布，如图9所示。测试中，首先在网格1上给出测试函数的准确分布，然后将其插值到网格2上，再插值回网格1，如此反复，进行200次插值后，将物理量分布与初始的准确分布进行比较，统计插值过程中的误差。分别采用常规二阶插值和守恒型二阶插值进行测试，并使用不同疏密的网格以分析插值方法的精度。测试中使用的4组网格的网格量如表1所示。

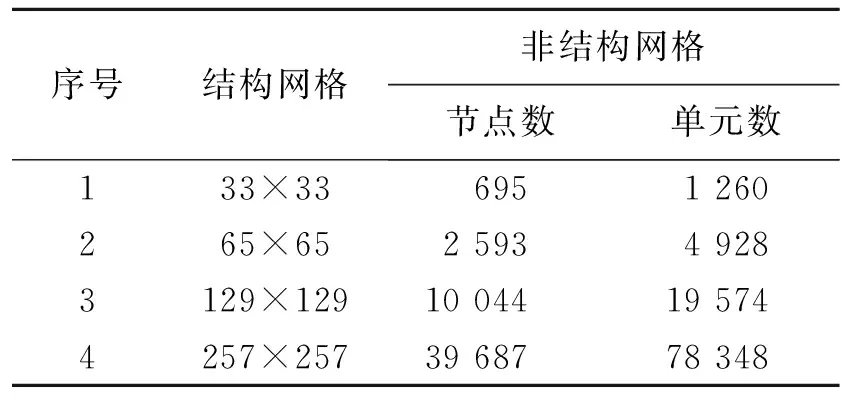
表1 计算网格参数Table 1 Parameters of the computational grid

图9 数值计算建模图Fig.9 Geometry of the specimen used for simulation

图10是计算误差与网格步长之间的关系，其中横坐标是表1中4个不同结构网格计算单元的边长，纵坐标代表计算区域内各单元函数分布插值后计算值与理论值之差的1范数。可以看出在相同的网格步长下，守恒型插值的误差更小，而且误差与网格步长之间的变化斜率更大，说明其具有更高阶的精度。计算结果表明，常规二阶插值精度约为1.4阶，而守恒型二阶插值精度约为1.87阶。表2是不同算例的守恒误差比较，守恒插值方法的守恒误差接近机器零，明显优于普通二阶插值。

表2 不同算例的守恒误差Table 2 Conservation errors indifferent numerical cases

图10 插值方法的精度比较Fig.10 Comparison of precision with different interpolation methods

算例3

考虑如下的测试函数：

φ(x,y,z)=1+sin(2πx)sin(2πy)sin(2πz)

计算区域是边长为1的正方体。每次测试使用两套网格，首先在网格1上给出测试函数的准确分布，然后将其插值到网格2上，再插值回网格1，如此反复，进行10次插值后，将物理量分布与初始的准确分布进行比较，统计插值过程中的误差。分别采用普通二阶插值和守恒型二阶插值进行测试，并使用不同疏密的网格以分析插值方法的精度。测试中使用的4组网格的网格量如表3所示，其中网格步长由下式得到：

式中：NE1和NE2分别为两套网格的单元个数，ND=3为网格的维数。

图11是测试函数在三维空间中的分布云图，图12是计算误差与网格步长之间的关系，其中横坐标是表3中dx的值，纵坐标代表计算区域内各单元函数分布插值后计算值与理论值之差的1范数。在三维条件下，守恒型插值依然具有更小的计算误差和更高的计算精度。

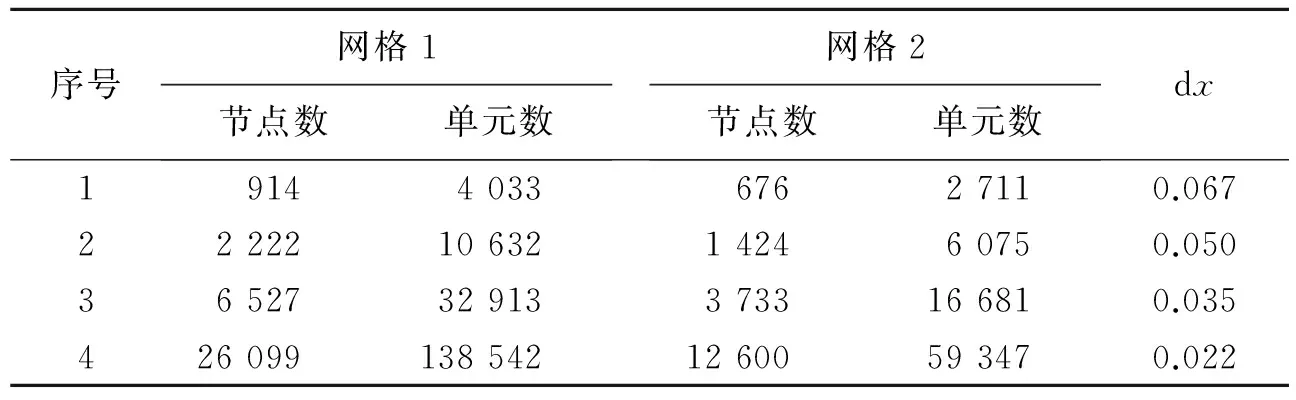
表3 计算网格参数Table 3 Parameters of the computational grid

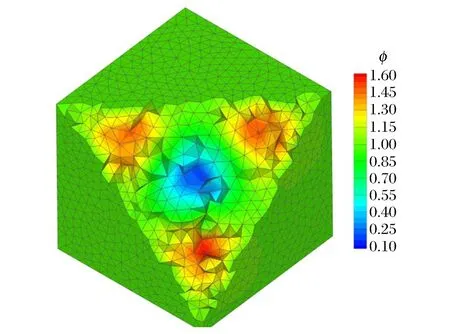
图11 测试函数分布云图Fig.11 Nephogram of different test functions

图12 插值方法的精度比较Fig.12 Comparison of precision with different interpolation methods

6 结 论

采用在新旧网格相交单元剖分构建出来的超级网格作为网格之间信息传递的基础，采用四叉树(二维)或八叉树(三维)方法搜寻算法提高计算效率，基于以上方法提出了网格之间流场物理量的守恒插值算法。该算法理论上可以实现网格之间物理量的精确守恒，二维和三维算例也表明产生的误差接近机器零，明显优于常用的二阶插值。本文中提出的方法可以解决爆轰流场模拟中网格尺度和物理量相差较大情况下的插值难题。

[1] 郭正,刘君,瞿章华.非结构动网格在三维可动边界问题中的应用[J].力学学报,2003,35(2):140-146. Guo Zheng, Liu Jun, Qu Zhanghua. Dynamic unstructured grid method with applications to 3d unsteady flows involving moving boundaries[J]. Acta Mechanica Sinica, 2003,35(2):140-146.

[2] Zeeuw D D, Powell K G. An adaptively refined Cartesian mesh solver for the Euler equations[J]. Journal of Computational Physics, 1993, 104(1),104:56-68.

[3] 白晓征.包含运动界面的爆炸流场数值模拟方法及其应用[D].长沙:国防科技大学,2009.

[4] 徐春光,白晓征,刘瑜,等.爆炸近区流场的数值模拟方法研究[J].兵工学报,2012,33(5):565-573. Xu Chunguang, Bai Xiaozheng, Liu Yu, et al. Research on numerical simulation method of near-field flows in air blast[J]. Acta Armmamentarii, 2012,33(5):565-573.

[5] Pärt-Enander E, Sjögreen B. Conservative and non-conservative interpolation between overlapping grids for finite volume solutions of hyperbolic problems[J]. Computers and Fluids, 1994,23(3):551-574.

[6] Margolin L G, Shashkov M. Second-order sign-preserving conservative interpolation (remapping) on general grids[J]. Journal of Computational Physics, 2002,184(1):266-298.

[7] Farrell P E, Piggott M D, Pain C C, et al. Conservative interpolation between unstructured meshes via supermesh construction[J]. Computer Methods in Applied Mechanics and Engineering, 2009,198(33/34/35/36):2632-2642.

[8] Farrell P E, Maddison J R. Conservative interpolation between volume meshes by local Galerkin projection[J]. Computer Methods in Applied Mechanics and Engineering, 2011,200(1/2/3/4):89-100.

[9] Menon S, Schmidt D P. Conservative interpolation on unstructured polyhedral meshes: An extension of the supermesh approach to cell-centered finite-volume variables[J]. Computer Methods in Applied Mechanics and Engineering, 2011,200(41/44):2797-2804.

[10] 郭正.包含运动边界的多体非定常流场数值模拟方法研究[D].长沙:国防科技大学,2002.

[11] 刘君,白晓征,郭正.非结构动网格计算方法----及其在包含运动界面的流场模拟中的应用[M].长沙:国防科技大学出版社,2009.

(责任编辑 曾月蓉)

An accurate conservative interpolation method for the mixed grid based on the intersection of grid cells

Xu Chunguang, Dong Haibo, Liu Jun

(SchoolofAeronauticsandAstronautics,DalianUniversityofTechnology,Dalian116024,Liaoning,China)

A method is presented for conservatively transferring cell-centered physical quantities from one mesh to another with second-order accuracy, which is well-suited for finite-volume methods that rely on cell-centered variables. The proposed methodology implements the cell-intersection algorithm of 2D/3D mixed grid based on the local supermesh idea, and is able to accurately calculate the intersection of any two polygons or polyhedrons, thus providing a basis for accurate conservative interpolation. The accuracy and the efficacy of the new method are demonstrated with multiple 2D and 3D numerical experiments. The test results show that this method ensures strict conservation of physical quantities in the interpolation process, and achieves a higher accuracy than that achieved by conventional second-order interpolation methods.

fluid mechanics; conservative interpolation; cell-intersection; mixed grid; local supermesh

10.11883/1001-1455(2016)03-0305-08

2014-11-10； < class="emphasis_bold">修回日期：2015-03-30

2015-03-30

国家自然科学基金项目(11272074);辽宁省自然科学基金项目(201202033)

徐春光(1977— )，男，博士,高级工程师;

刘 君,liujun65@dlut.edu.cn。

O354 <国标学科代码：13025 class="emphasis_bold"> 国标学科代码：13025 文献标志码：A国标学科代码：13025

A