弹丸入水特性的SPH计算模拟*

周 杰，徐胜利

(清华大学航天航空学院，北京 100084)

弹丸入水特性的SPH计算模拟*

周 杰，徐胜利

(清华大学航天航空学院，北京 100084)

应用SPH方法研究弹丸入水过程中的动力学特征。利用拉格朗日形式的N-S方程自编SPH程序，建立弹丸入水的计算模型，赋予相应的材料参数及状态方程，研究弹丸外形、入水速度和角度等因素对入水过程的影响。模拟结果表明：空化泡的形态及发展规律主要由弹丸的运动姿态决定；弹道越稳定，阻力因数就越小，弹丸的存速就越大。SPH方法具有较强的自适应性，适用于研究弹丸入水的流固耦合问题。

流体力学；水下弹道；SPH；阻力因数

高速弹丸入水在反潜扫雷等方面有重要应用前景。该问题属于典型的流固耦合问题，涉及自由面破碎及其追踪、水空化和相变、受冲击载荷作用引起的弹丸形变和断裂、弹水动态流固耦合(水动弹性)等复杂物理过程[1]。采用简化的理论模型只能分析空化泡形态等非耦合过程[2]。Logvinovich[3]提出空穴截面扩张的独立原理，这个原理是近似的，但用它可以很简单地确定各种情况下空化泡的外形。曹伟等[4]通过实验研究了高速射弹的自然超空泡形态和发展规律。易文俊等[5]基于Rayleigh-Plesset单一介质可变密度混合多相流模型，计算分析了不同射弹的超空泡减阻特性。安伟光等[6]依据气体泄漏规则建立空泡内气体平衡方程，联合空泡截面扩展及运动体姿态方程，数值研究了运动体带空泡高速入水非定常过程。数值模拟非常适合求解上述多个耦合过程，其中无网格的光滑粒子流体动力学(smoothed particle hydrodynamics, SPH)方法适合求解弹丸入水过程中介质大变形和流固耦合问题[7-8]。

本文中基于SPH方法，分析弹丸外形、入水速度和角度等因素对弹丸入水过程的影响，对弹丸入水过程中产生的空泡形态、弹道轨迹和弹丸阻力因数等进行模拟计算，研究弹丸入水的机理，为分析弹丸稳定性和阻力等提供理论依据。

1 计算模型和数值方法

1.1 计算模型

设计3种外形的弹丸，以不同角度、速度入水，研究其入水过程的动力学特性及水中弹道规律。图1给出了3种弹丸及入水模型的示意图。弹丸以初速度v0、角度θ进入H×L的水域的计算模型，水域的边界条件设置为固壁边界。弹丸有3种类型：(A) 平头弹丸的长度L1=40 mm，直径D=12 mm；(B) 尖头弹丸的长度L2=20 mm、L3=20 mm，直径D=12 mm；(C) 截断头弹丸的长度L2=20 mm、L4=10.44 mm，弹丸直径D=12 mm，截断面直径D1=6 mm。弹丸入水初速度v0分别为1 200、200 m/s，入水角度θ取90°、60°、30°。

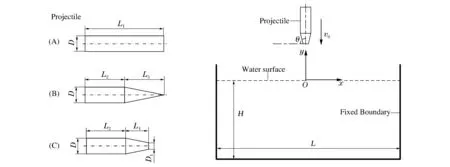
图1 弹丸外形及入水示意图Fig.1 Schematic diagram of the projectile shape and projectile entry into the water

1.2 状态方程

冲击载荷作用下，通常采用 Mie-Grüneisen状态方程来描述水的动力学性质[9]。水的状态方程取决与水的状态，在压缩和膨胀状态下水的压力分别为：

(1)

式中：p为水的压力；ρ0是初始密度；η是扰动前后的密度比，μ=η-1，当μ>0时，水处于压缩状态，当μ<0时，水处于膨胀状态；γ0为Grüneisen常数，a为体积修正系数；c为水中的声速，S1、S2、S3均为实验拟合系数。水的相关参数如表1所示。

表1 Mie-Grüneisen状态方程的材料参数Table 1 Material parameters of Mie-Grüneisen equation of state

弹丸假定为理想弹塑性体，静水压力与体积变化率之间呈线性变化，相关方程如下[10]：

dps=KdεV

(2)

式中：ps为静水压力；εV为材料应变；K为体积模量，K=E/[3(1-2ν)]，E为弹性模量，ν为泊松比。弹丸的密度为7 800 kg/m3，弹性模量为210 GPa，泊松比为0.3。

1.3 SPH方法

光滑粒子流体动力学(SPH)方法是由L.B.Lucy等[11]提出的一种解决天体物理学问题的纯拉格朗日方法，后来该方法被用于研究介质大变形及流固耦合问题[12]，在求解过程中展示出无网格方法所特有的强大的自适应性。SPH方法的核心思想：用一系列任意分布的粒子来表示问题域，用积分表示法来近似场函数，应用粒子来对核近似方程进一步近似，在每个时间步内都要进行粒子近似的过程，将粒子近似法应用于描述场函数的偏微分方程，得到只与时间相关的离散化形式的常微分方程，应用积分法来求解常微分方程，得到粒子的场变量。以上特点结合起来，使得SPH方法成为具有无网格、自适应、稳定等特点以及拉格朗日性质的动力学问题求解方法，非常适合求解弹丸入水过程中介质大变形和流固耦合问题。

与有限元方法不同，SPH方法的节点是离散的。该方法采用光滑长度内的粒子代替有限元方法中的影响节点集。因为没有固定的单元体连接，SPH方法中的每个粒子周围光滑长度内的粒子个数和分布是不固定的，采用J.J.Monaghan[13]提出的B-样条函数的光滑函数，用积分表示法来近似某一点的场函数值。为了使SPH算法适合模拟冲击问题，引入Monaghan型人工黏度[14]。弹丸入水问题中水域有2种不同边界：自由边界和固壁边界。由于SPH方法的自适应性，自由液面处的粒子可以自动跟随液面运动，不需要做特殊处理。固壁边界采用排斥边界条件，在壁面外设置一组虚拟粒子，虚拟粒子参与流体粒子计算，粒子自身密度也不断更新，但位置和速度保持不变[14]。采用蛙跳法求解具有拉格朗日性质的SPH方法的N-S方程[12]，时间步长满足CFL条件[15]。

2 计算结果分析和讨论

本文中研究3种外形的弹丸，以不同初速度v0、角度θ入水，计算空泡形态、弹道轨迹、及速度的变化规律，了解影响弹丸动力学特征的相关因素。

2.1 弹道轨迹

图2(a) 尖头弹丸入水的空化泡形状发展(θ=90°)Fig.2(a) Shape formation of cavitation bubble during the cuspidal projectile entry into the water (θ=90°)

图2给出了尖头弹丸以初速度v0=1 200 m/s，不同角度θ入水的空化泡形状的发展规律。由图可知：(1)弹丸垂直入水时，空化泡的长度、宽度是随着运动时间(t)增加而变大的，空化泡的长度的变化率要大于空化泡宽度，各时刻的空化泡形态保持几何相似，且关于y轴对称，在计算时间内空化泡的没有出现闭合现象，如图2(a)所示；(2)弹丸以θ为60°和30°入水时，空化泡的长度、宽度随着运动时间增加而变大，空化泡没有出现闭合现象，由于受到偏转力矩作用，弹丸的运动轨迹是弧形的，导致空化泡不再是轴对称的形状，各时刻空化泡头部的形状、及运动规律主要是由弹丸姿态决定的，如图2(b)和2(c)所示。

图2(b) 尖头弹丸入水的空化泡形状发展(θ=60°)Fig.2(b) Shape formation of cavitation bubble during the cuspidal projectile entry into the water (θ=60°)

图2(c) 尖头弹丸入水的空化泡形状发展(θ=30°)Fig.2(c) Shape formation of cavitation bubble during the cuspidal projectile entry into the water (θ=30°)

图3是尖头弹丸以v0=1 200 m/s，θ=60°入水的计算结果。由图可知：(1)t=0.1 ms时，弹丸高速进入水域，弹丸的运动方向保持与入水前一致；(2)t=0.2和0.3 ms时，由于弹丸入水角度θ=60°，因此在水中运动时会受到一个偏转力矩作用，引起弹丸的运动姿态发生变化，导致弹丸运动方向相对于入水前偏转了较大的角度(弹道失稳)，且弹丸周围产生空化泡；(3)t=0.5和0.7 ms时，随着弹丸的稳定性的下降，弹道偏转现象越来越明显，弹丸周围形成了一个不闭合的弧形空泡，且速度急剧下降。

图3 尖头弹丸的入水轨迹(v0=1 200 m/s，θ=60°)Fig.3 Trajectory of cuspidal projectile entry into the water (v0=1 200 m/s，θ=60°)

图4是平头弹丸以v0=1 200 m/s，θ=90°入水的计算结果。由图可知：(1)t=0.08 ms时，弹丸高速进入水域，会在弹头边界形成应力集中，导致边界产生裂纹；(2)t=0.2 ms时，弹头边界部分出现断裂现象，破片与弹丸分离，弹头变化为锥形凸台，且弹丸周围有空化泡产生；(3)t=0.4和0.6 ms时，随着弹丸在水中运动，空泡半径越来越大，产生的破片以较大的速度向两侧运动，同样也会产生空化泡，对弹丸周围的空化泡产生影响；(4)t=0.8 ms时，弹丸的运动速度越来越小，弹丸周围形成闭合空泡。

图4 平头弹入水运动轨迹(v0=1 200 m/s，θ=90°)Fig.4 Trajectory of blunt projectile entry into the water (v0=1 200 m/s，θ=90°)

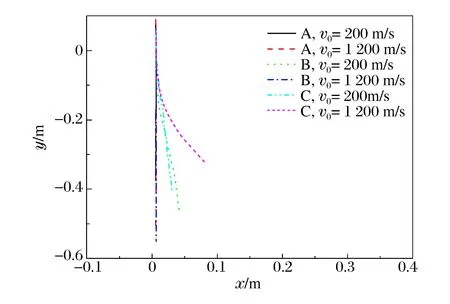
图5(a) 弹丸入水过程中的弹道轨迹(θ=90°)Fig.5(a) Ballistic trajectory of projectile during the process of entry into the water (θ=90°)

图5给出了3种弹丸在高速和低速下的弹道轨迹，其中：A、B、C分别代表平头、尖头和截断头的弹丸。图5(a)为弹丸垂直入水的弹道轨迹：平头弹丸在高、低速条件下，弹道轨迹均保持良好的稳定性；尖头弹丸在高速情况下弹道稳定性良好，而低速情况下弹道则失稳；截断头弹丸在高、低速条件下，弹道轨迹均失稳。图5(b)和5(c)分别是弹丸入水角度θ=60°和30°的弹道轨迹：低速情况下，3种弹丸的弹道轨迹均能保证良好的稳定性；而在高速情况下弹丸的弹道轨迹的稳定性均会变的不理想，尤其是尖头弹丸。实际上，弹丸在水中的弹道轨迹主要是由弹丸的质心、压心的位置关系决定的，设计弹丸外形时应给予考虑，如对于大长径比的弹丸，应该考虑通过摆动(尾拍)保持弹丸运动平衡。

图5(b) 弹丸入水过程中的弹道轨迹(θ=60°)Fig.5(b) Ballistic trajectory of projectile during the process of entry into the water (θ=60°)

图5(c) 弹丸入水过程中的弹道轨迹(θ=30°)Fig.5(c) Ballistic trajectory of projectile during the process of entry into the water (θ=30°)

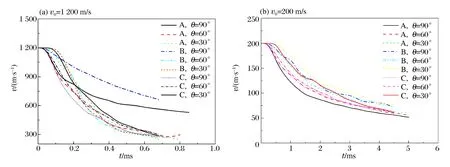
图6 弹丸入水的速度变化规律Fig.6 Profile of the velocity variation during the projectile entry into the water

2.2 运动规律

图6给出了3种弹丸在不同入水角度下的速度。图6(a)为弹丸入水速度v0=1 200 m/s的运动规律。垂直入水的情况下，尖头弹丸产生的空化泡有效的降低了水的阻力，而截断头弹的弹道轨迹发生了偏转现象，所以受到的阻力较大，速度下降的最为明显；θ=60°和30°时，3种类型的弹丸在水中运动的稳定性均比较差，受到的水的阻力均较大，尤其是尖头弹丸，速度下降的最为明显。图6(b)为弹丸入水速度v0=200 m/s的运动规律：垂直入水时，3种弹丸的入水速度大小关系为vB>vC>vA；θ=60°和30°时，则为vB>vC≈vA。

根据牛顿第二定律，在水中运动的弹丸质心运动方程为：

(3)

式中：m为弹丸质量，v为弹丸运动速度，Rx为弹丸受到的阻力，Ry为升力，Rz为马格努斯力，Rg为重力，RC为科氏力升力，RΩ为地球自转产生的惯性力。计算中只考虑阻力Rx=-0.5ρwv2CxS，ρw是水的密度，Cx是弹丸阻力因数，S是垂直中心轴的最大截面积。

图7给出了不同速度下，阻力因数随时间的变化规律。弹丸入水速度v0=1 200 m/s时：垂直入水的情况下，平头弹入水的初始阻力因数较大，随着弹丸的破坏，弹头形状变为锥形凸台，有效的降低了阻力因数，尖头弹的阻力因数较小，随着时间增长保持在0.5左右，而截断头弹丸的弹道轨迹发生了偏转现象，所以阻力因数均较大；入水角度为60°、30°的情况下，3种类型的弹丸的阻力因数较垂直入水时大，3种弹丸的阻力因数从大到小依次为平头弹、尖头弹、截断头弹。弹丸入水速度v0=200 m/s时，平头弹丸的阻力因数明显要高于其他的2种弹形；尖头弹、截断头弹的阻力因数均在1.2附近震荡。

图7 弹丸阻力因数随时间的变化规律Fig.7 Variation of the projectile's drag coefficient with time

3 结 论

本文中采用具有无网格、自适应、稳定以及拉格朗日性质的SPH方法，研究了不同外形弹丸以不同初速度、角度入水的动力学过程：

(1) 弹丸入水时，如果弹道轨迹稳定，会产生对称的空化泡，否则会产生不规则的空化泡，空化泡的形态及发展规律主要由弹丸的运动姿态决定；

(2) 垂直入水时，高速条件下平头和尖头弹丸的弹道轨迹稳定性较好，低速条件下只有平头弹丸的弹道稳定；以一定角度入水时，3种外形弹丸在低速条件下的弹道稳定性要优于高速条件；弹道稳定性是由弹丸的质心、压心的位置关系决定的；

(3) 垂直高速入水时，尖头弹丸的阻力因数最小，而以一定角度高速入水时，截断头弹阻力因数最小；低速入水时，平头弹的阻力因数较大，而尖头弹、截断头弹的阻力因数大小相当；

(4) 弹道稳定性越好，阻力因数就越小，弹丸的存速就越大；阻力因数的大小还与弹丸头部空化器的尺寸相关。

[1] Putilin S I. Some features of dynamics of supercavitating models[J]. Applied Hydromechanics, 2000,2(74):65-74.

[2] Knapp R T, Daily J W, Hammitt F G. Cavitation[M]. NewYork: McGraw-Hill, 1970.

[3] Franc J-P, Michel J-M. Fundamentals of cavitation[M]. The Netherlands: Kluwer Academic Publishers, 2004

[4] 曹伟，王聪，魏英杰，等.自然超空泡形态特性的射弹试验研究[J].工程力学,2006,23(12):175-187. Cao Wei, Wang Cong, Wei Yingjie, et al. High-speed projectile experimental investigations on the characteristics of natural supercavitation[J]. Engineering Mechanics, 2006,23(12):175-187.

[5] 易文俊,王中原,熊天红,等.水下高速射弹超空泡减阻特性研究[J].弹道学报,2008,20(4):1-4. Yi Wenjun, Wang Zhongyuan, Xiong Tianhong, et al. Research on drag reduction characteristics of a underwater high-speed supercavitation projectile [J]. Journal of Ballistics, 2008,20(4): 1-4.

[6] 安伟光,蒋运华,安海.运动体高速入水非定常过程研究[J].工程力学,2011,28(3):251-256. An Weiguang, Jiang Yunhua, An Hai. The unsteady water entry process study of high-speed vehicle[J]. Engineering Mechanics, 2011,28(3):251-256.

[7] Chen J K, Beraun J E. A generalized smoothed particle hydrodynamic method for nonlinear dynamic problems[J]. Computer Methods in Applied Mechanics and Engineering, 2000,190(1):225-239.

[8] Cleary P W, Prakash M, Ha J. Novel applications of smoothed particle hydrodynamics (SPH) in metal forming[J]. Journal of Materials Processing Technology, 2006,177(1):41-48.

[9] Shin Y S, Lee M, Lam K Y, et al. Modeling mitigation effects of watershield on shock wave[J]. Shock and Vibration, 1998,5(4):225-234.

[10] Libersky L D, Petschek A G. High strain Lagrangian hydrodynamics: A three-dimensional SPH code for dynamic material response[J]. Journal of Computational Physics, 1993,109(1):67-75.

[11] Lucy L B. A numerical approach to the testing of the fission hypothesis[J]. The Astronomical Journal, 1977,82(12):1013-1024.

[12] Liu G R, Liu M B. Smoothed particle hydrodynamics: A meshfree particle method[M]. German: Springer Berlin /Heidelberg, 2004:1-491．

[13] Monaghan J J. Particle methods for hydrodynamic[J]. Computer Physics Report,1985,3(2):71-124.

[14] Monaghan J J. On the problem of penetration in particle menthods[J]. Journal of Computer Physics, 1989,82(1):1-15.

[15] Monaghan J J. Smoothed particle hydrodynamics[J]. Reports on Progress in Physics, 2005,68(8):1703-1759.

(责任编辑 王小飞)

SPH simulation on the behaviors of projectile water entry

Zhou Jie, Xu Shengli

(SchoolofAerospaceEngineering,TsinghuaUniversity,Beijing100084,China)

In this work we investigated the dynamic behaviors of the projectile water entry using the SPH method. We developed our own SPH program based on the N-S equation of the Lagrange form and established a calculation model for the projectile water entry and, with corresponding material parameters and equation of state given, studied the influence of such factors as projectile shape, velocity and angle into the water on the process of the projectile water entry. The simulation results show that the formation and the development of the cavitation bubble are mainly determined by the projectile's state of motion: the more stable the projectile's trajectory, the smaller its drag coefficient, and the greater its sustained velocity. It is found that the SPH method has a high self-adaptability, for which it is applicable for studying the problems related with fluid-structure interaction occurring during the process of the projectile water entry.

fluid mechanics; underwater trajectory; SPH; drag coefficient

10.11883/1001-1455(2016)03-0326-07

2014-09-22；

2014-12-05

中国博士后科学基金面上项目(2015M581081)

周 杰(1986- )，男，博士，Beijihu1986@163.com。

O352国标学科代码：13025

A